- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии 10 класс по теме Прямоугольный параллелепипед, куб
Содержание
- 1. Презентация к уроку геометрии 10 класс по теме Прямоугольный параллелепипед, куб
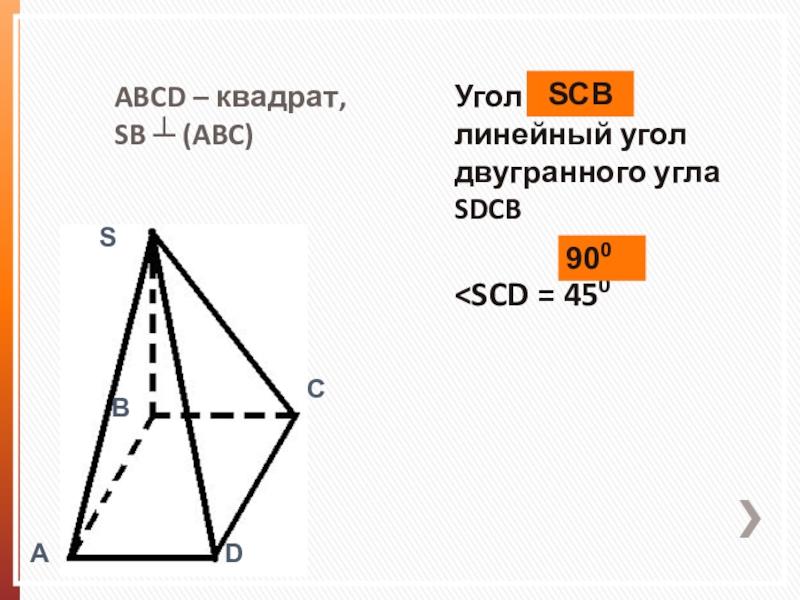
- 2. ABCD – квадрат, SB ┴ (ABC)Угол
- 3. Вставьте пропущенные символы, знаки, закончите предложение, чтобы
- 4. Задача 2Дан тетраэдр SABC, ABC – прямоугольный
- 5. ПРЯМОУГОЛЬНЫЙ
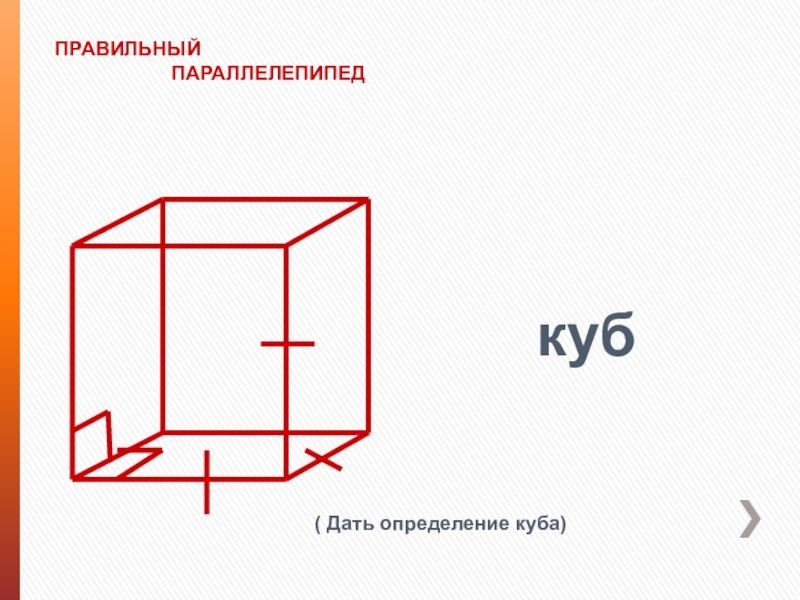
- 6. ПРАВИЛЬНЫЙ
- 7. Свойство 1 В прямоугольном параллелепипеде все шесть граней прямоугольники.
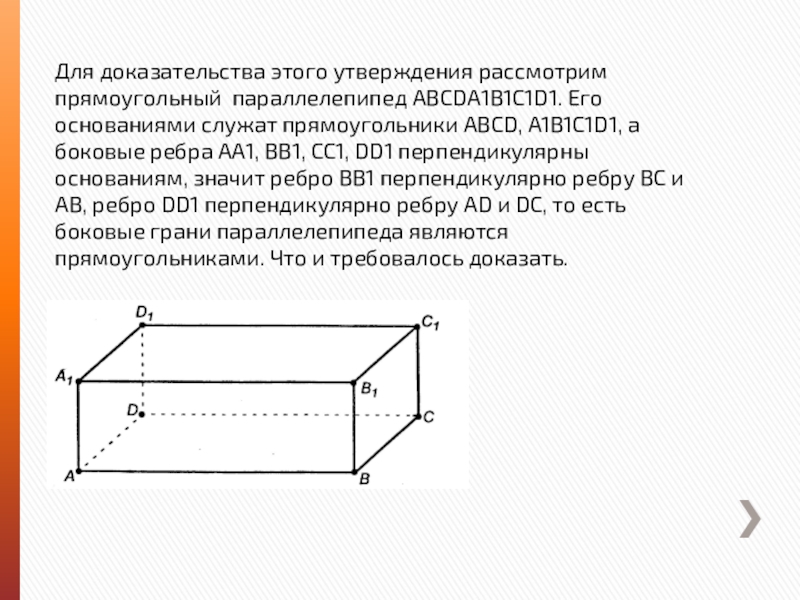
- 8. Для доказательства этого утверждения рассмотрим прямоугольный параллелепипед
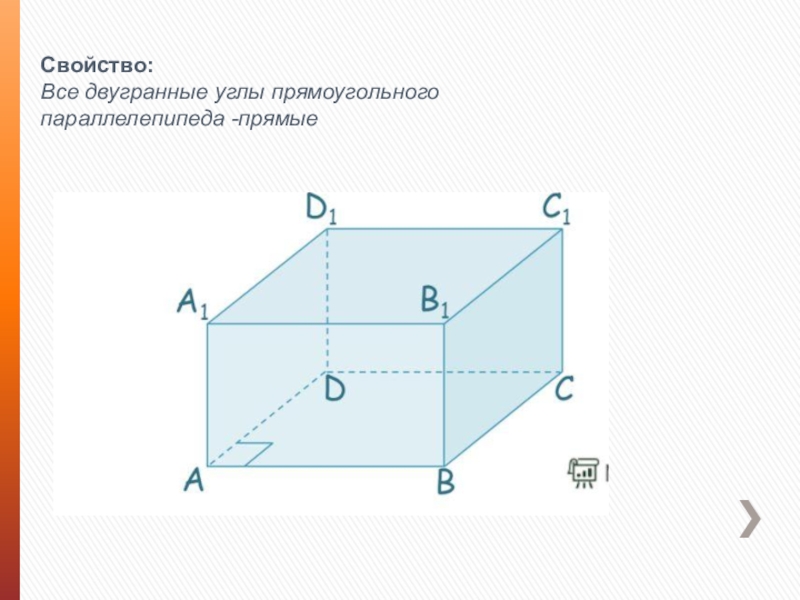
- 9. Свойство:Все двугранные углы прямоугольного параллелепипеда -прямые
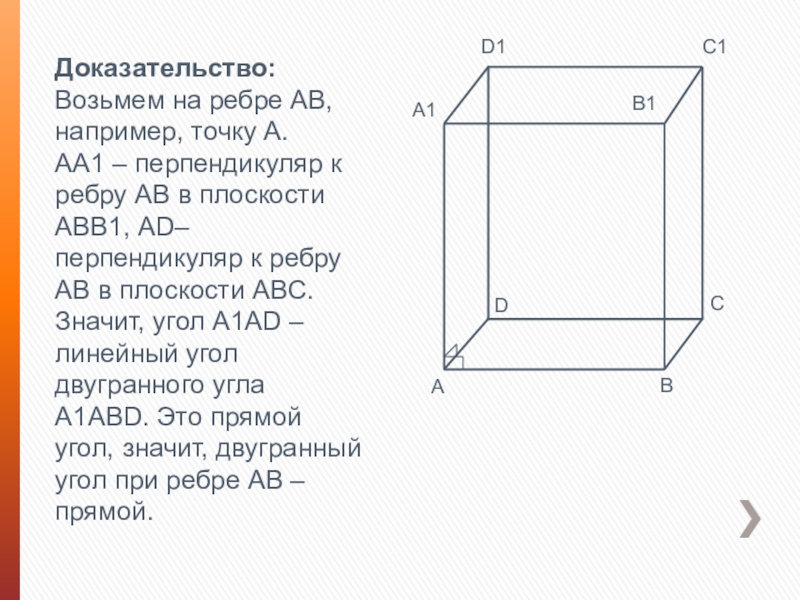
- 10. Доказательство:Возьмем на ребре AB, например, точку А.
- 11. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений
- 12. Дано: АВСDА1В1С1D1 – прямоугольныйпараллелепипедДоказать: AC1^2=AB^2+AD^2+AA1^2Доказательство:Прямая СС1 перпендикулярна
- 13. Задача 3 Основанием прямоугольного параллелепипеда
- 14. Задача 4 Три измерения прямоугольного
- 15. Задача 5ABCDA1 B1C1D1 - прямоугольный параллелепипед ABCDA1B1C1D1Треугольник
- 16. ПРИМЕР ПАРАЛЛЕЛЕПИПЕДА В АРХИТЕКТУРЕ
- 17. Слайд 17
- 18. Слайд 18
- 19. ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ ФОРМЫ ПАРАЛЛЕЛЕПИПЕДА В БЫТУ
- 20. Слайд 20
- 21. Самостоятельная работа
- 22. Домашнее задание: глава 2, параграф 22-24№ 192, 194
ABCD – квадрат, SB ┴ (ABC)Угол SCD - линейный угол двугранного угла SDCB
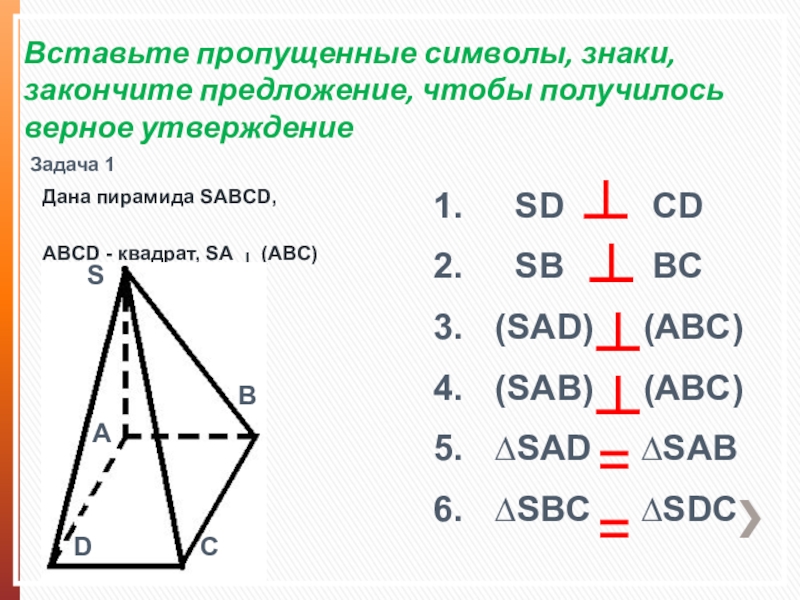
Слайд 3Вставьте пропущенные символы, знаки, закончите предложение, чтобы получилось верное утверждение
Задача 1
Дана
пирамида SABCD,
ABCD - квадрат, SA ┴ (ABC)
ABCD - квадрат, SA ┴ (ABC)
SD CD
SB BC
(SAD) (ABC)
(SAB) (ABC)
∆SAD ∆SAB
∆SBC ∆SDC
A
B
C
D
S
┴
┴
┴
┴
=
=
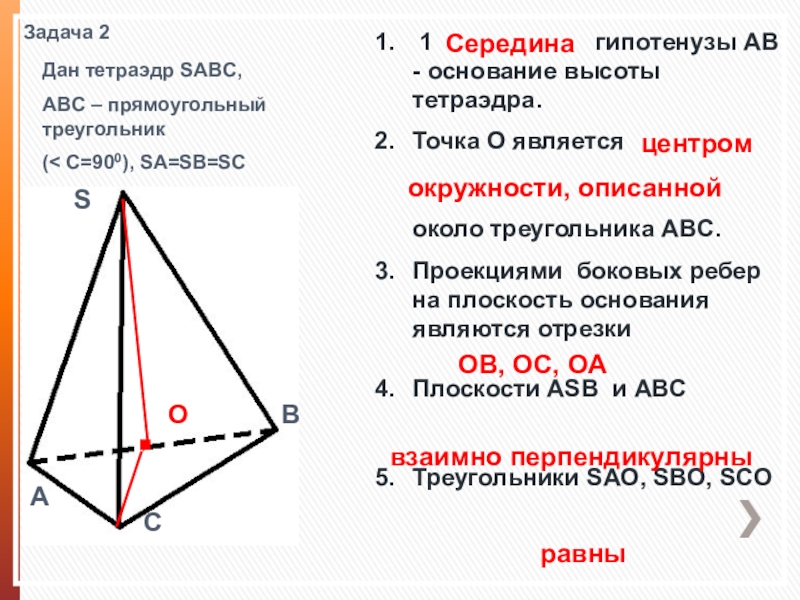
Слайд 4Задача 2
Дан тетраэдр SABC,
ABC – прямоугольный треугольник
(< C=900), SA=SB=SC
1.
гипотенузы AB - основание высоты тетраэдра.
Точка О является около треугольника ABC.
Проекциями боковых ребер на плоскость основания являются отрезки
Плоскости ASB и ABC
Треугольники SAO, SBO, SCO
Точка О является около треугольника ABC.
Проекциями боковых ребер на плоскость основания являются отрезки
Плоскости ASB и ABC
Треугольники SAO, SBO, SCO
Середина
центром
окружности, описанной
OB, OC, OA
.
взаимно перпендикулярны
равны
S
A
B
C
O
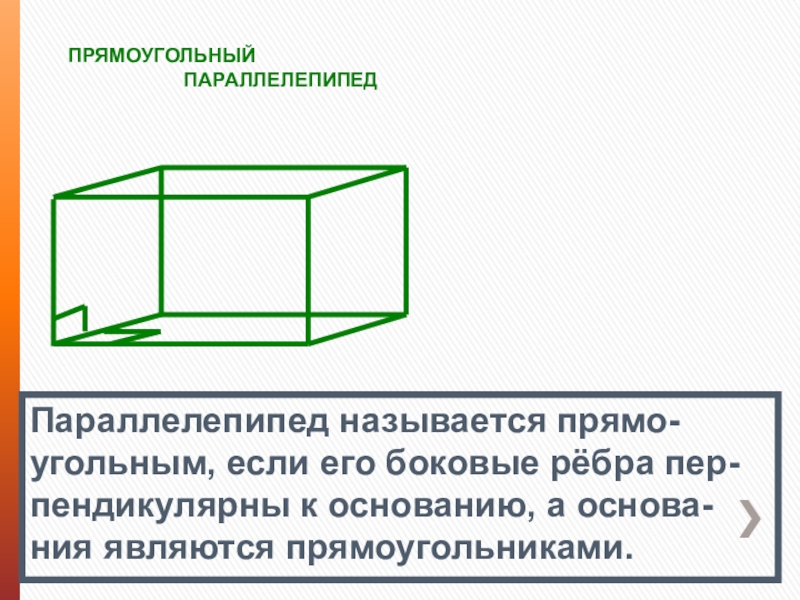
Слайд 5ПРЯМОУГОЛЬНЫЙ
ПАРАЛЛЕЛЕПИПЕД
Параллелепипед называется прямо-
угольным, если его боковые рёбра пер- пендикулярны к основанию, а основа- ния являются прямоугольниками.
Слайд 8Для доказательства этого утверждения рассмотрим прямоугольный параллелепипед АВСDА1B1C1D1. Его основаниями служат
прямоугольники АВСD, A1B1C1D1, а боковые ребра АА1, ВВ1, СС1, DD1 перпендикулярны основаниям, значит ребро ВВ1 перпендикулярно ребру ВС и АВ, ребро DD1 перпендикулярно ребру АD и DС, то есть боковые грани параллелепипеда являются прямоугольниками. Что и требовалось доказать.
Слайд 10
Доказательство:
Возьмем на ребре AB, например, точку А. AA1 – перпендикуляр к ребру
AB в плоскости ABB1, АD– перпендикуляр к ребру АB в плоскости ABC. Значит, угол A1AD – линейный угол двугранного угла А1АВD. Это прямой угол, значит, двугранный угол при ребре AB – прямой.
А
В
С
D
А1
В1
С1
D1
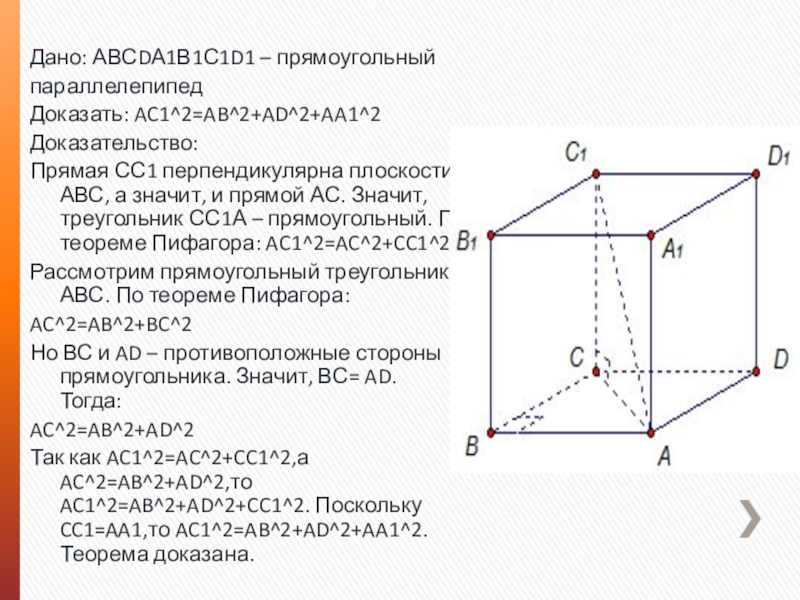
Слайд 12Дано: АВСDА1В1С1D1 – прямоугольный
параллелепипед
Доказать: AC1^2=AB^2+AD^2+AA1^2
Доказательство:
Прямая СС1 перпендикулярна плоскости АВС, а значит,
и прямой АС. Значит, треугольник СС1А – прямоугольный. По теореме Пифагора: AC1^2=AC^2+CC1^2
Рассмотрим прямоугольный треугольник АВС. По теореме Пифагора:
AC^2=AB^2+BC^2
Но ВС и AD – противоположные стороны прямоугольника. Значит, ВС= AD. Тогда:
AC^2=AB^2+AD^2
Так как AC1^2=AC^2+CC1^2,а AC^2=AB^2+AD^2,то AC1^2=AB^2+AD^2+CC1^2. Поскольку CC1=AA1,то AC1^2=AB^2+AD^2+AA1^2. Теорема доказана.
Рассмотрим прямоугольный треугольник АВС. По теореме Пифагора:
AC^2=AB^2+BC^2
Но ВС и AD – противоположные стороны прямоугольника. Значит, ВС= AD. Тогда:
AC^2=AB^2+AD^2
Так как AC1^2=AC^2+CC1^2,а AC^2=AB^2+AD^2,то AC1^2=AB^2+AD^2+CC1^2. Поскольку CC1=AA1,то AC1^2=AB^2+AD^2+AA1^2. Теорема доказана.
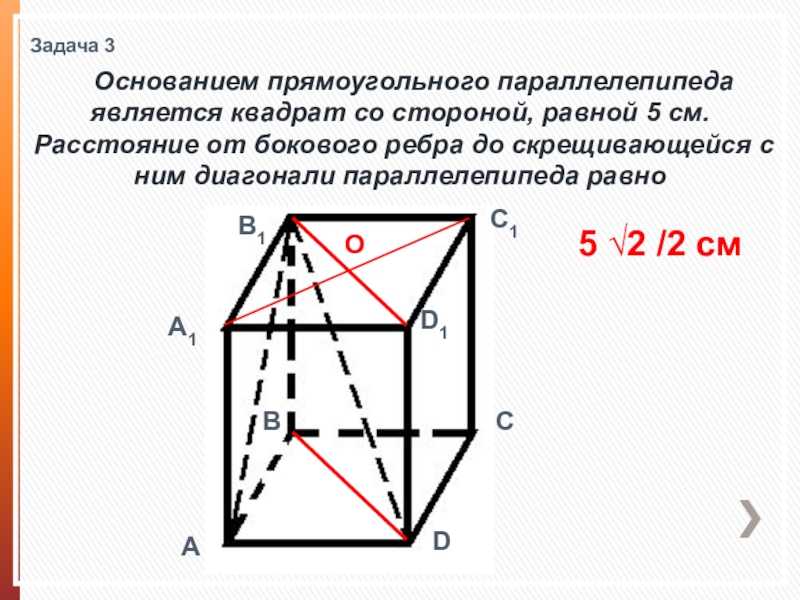
Слайд 13Задача 3
Основанием прямоугольного параллелепипеда является квадрат со стороной,
равной 5 см. Расстояние от бокового ребра до скрещивающейся с ним диагонали параллелепипеда равно
A
B
C
D
A1
B1
C1
D1
5 √2 /2 см
О
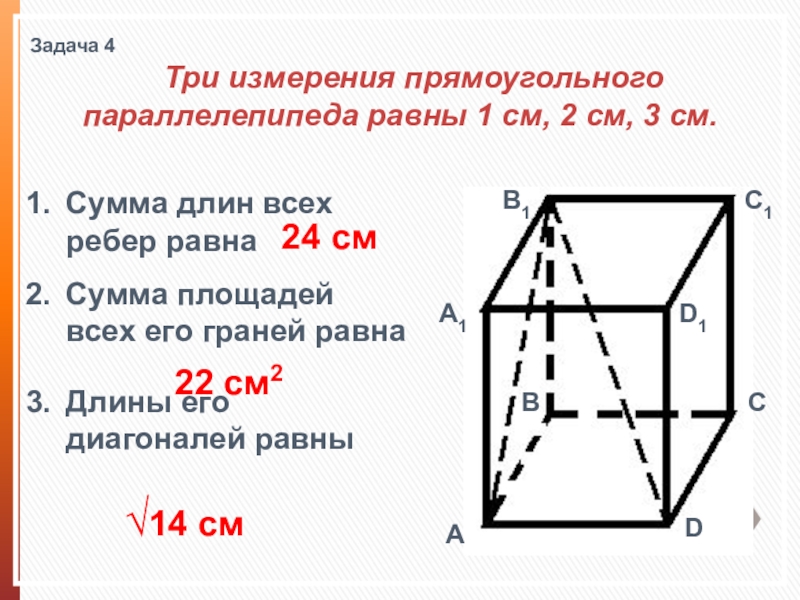
Слайд 14Задача 4
Три измерения прямоугольного параллелепипеда равны 1 см,
2 см, 3 см.
A
B
C
D
A1
B1
C1
D1
Сумма длин всех ребер равна
Сумма площадей всех его граней равна
Длины его диагоналей равны
24 см
22 см2
√14 см
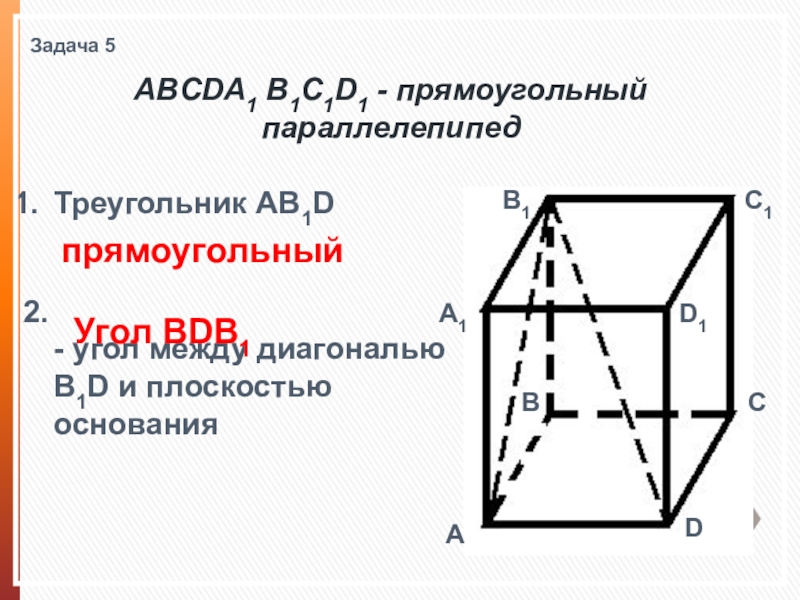
Слайд 15Задача 5
ABCDA1 B1C1D1 - прямоугольный параллелепипед
A
B
C
D
A1
B1
C1
D1
Треугольник AB1D
2.
- угол между диагональю
B1D и плоскостью основания
прямоугольный
Угол BDB1
Слайд 21Самостоятельная работа
В прямоугольном параллелепипеде
измерения равны
6 см, 8 см, 10 см.
Найдите диагональ параллелепипеда и синус угла между диагональю параллелепипеда и плоскостью его основания
Найдите диагональ параллелепипеда и синус угла между диагональю параллелепипеда и плоскостью его основания
В прямоугольном параллелепипеде измерения равны
5 см, 7 см, √ 47 см.
Найдите диагональ параллелепипеда и синус угла между диагональю параллелепипеда и плоскостью его основания
Вариант 1
Вариант 2
