- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Двугранный угол геометрия 10 класс
Содержание
- 1. Презентация к уроку Двугранный угол геометрия 10 класс
- 2. Расстояние от точки до прямой – длина
- 3. ВСMИз точки В к плоскости проведена наклонная,
- 4. ВСMАИз точки В к плоскости проведены две
- 5. ВСMАИз точки В к плоскости проведены две
- 6. ВСMАИз точки В к плоскости проведены две
- 7. П-я Через вершину С треугольника АВС проведена
- 8. ПланиметрияСтереометрияУглом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из одной точки.Двугранный угол
- 9. Двугранным углом называется фигура, образованная прямой a
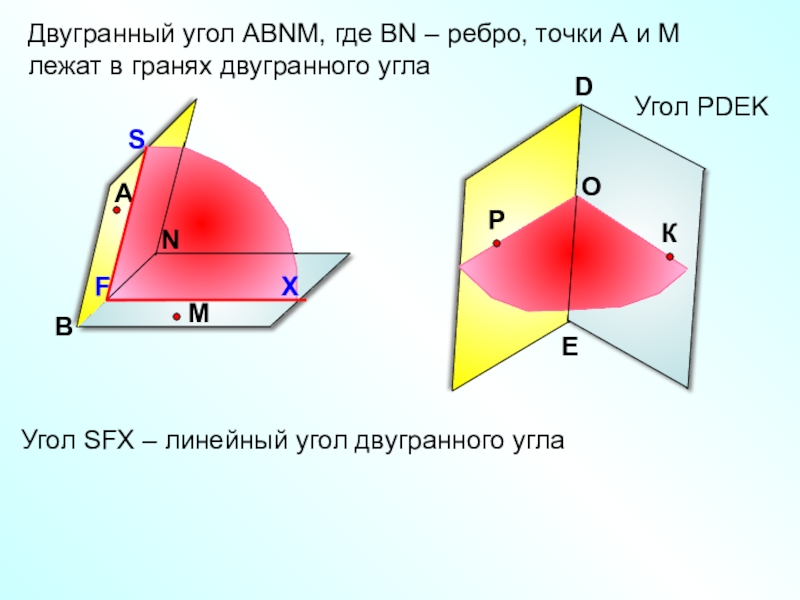
- 10. Угол РDEK Двугранный угол АВNМ, где ВN
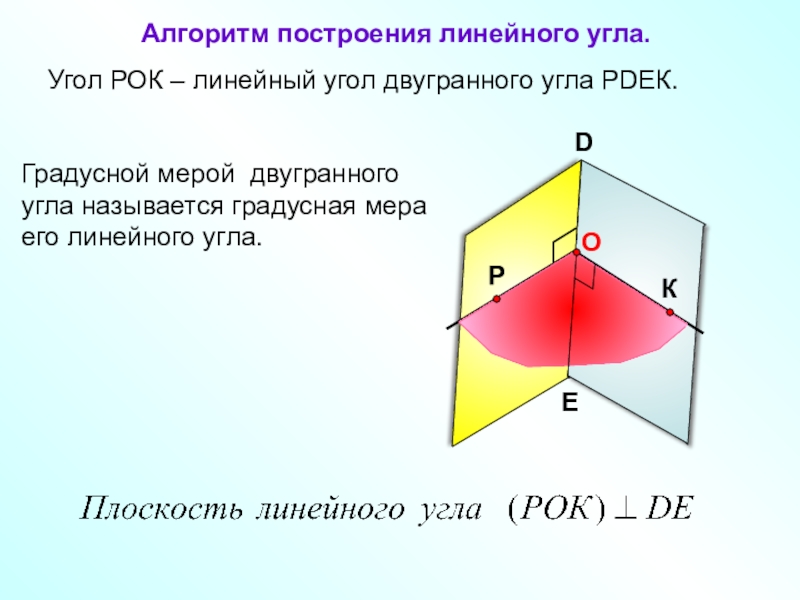
- 11. Угол РОК – линейный угол двугранного угла
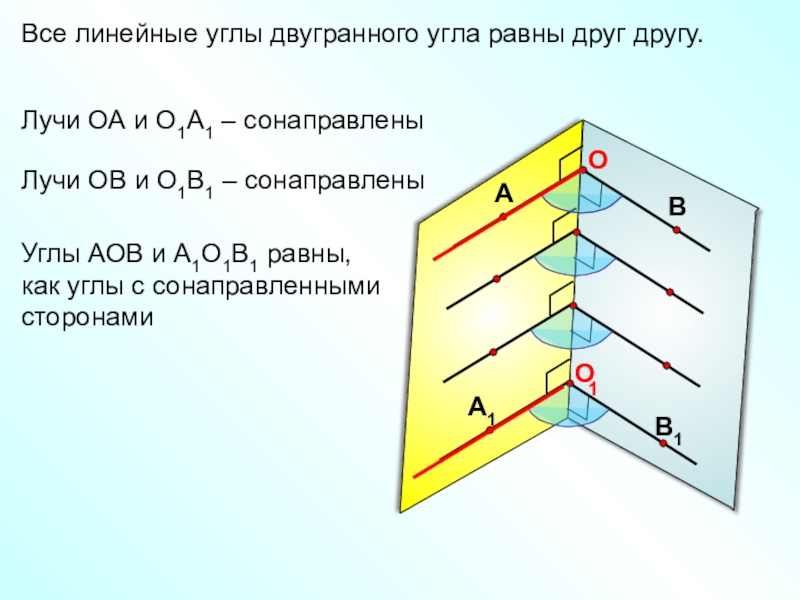
- 12. Все линейные углы двугранного угла равны друг
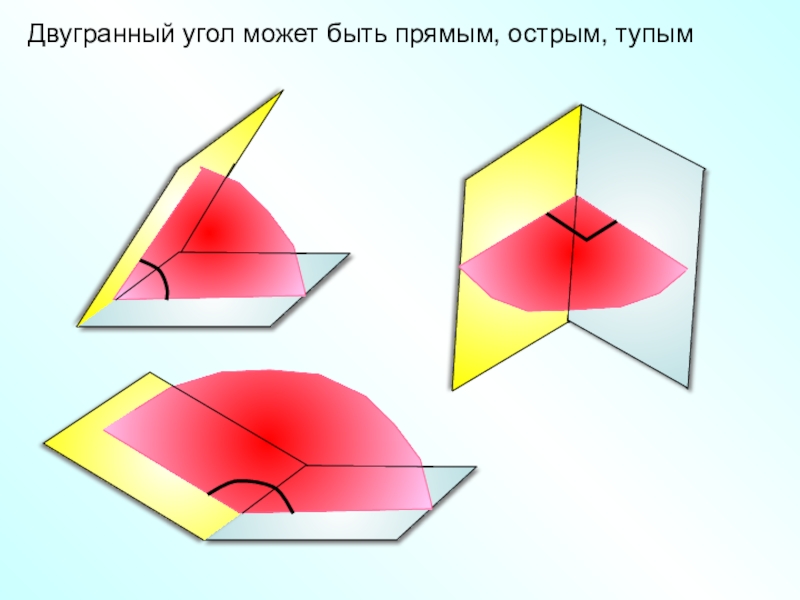
- 13. Двугранный угол может быть прямым, острым, тупым
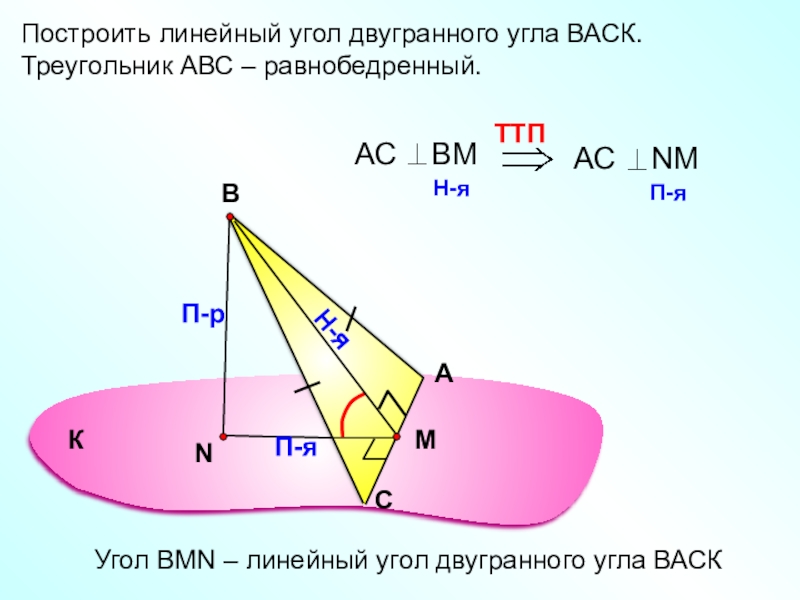
- 14. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – равнобедренный.АСВП-рН-яП-яУгол ВMN – линейный угол двугранного угла ВАСКК
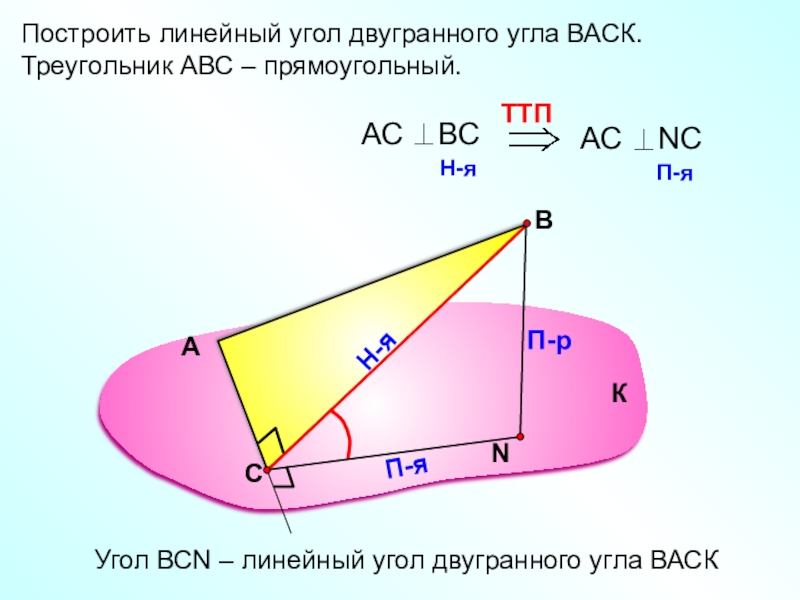
- 15. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – прямоугольный.АВП-рН-яП-яУгол ВСN – линейный угол двугранного угла ВАСККС
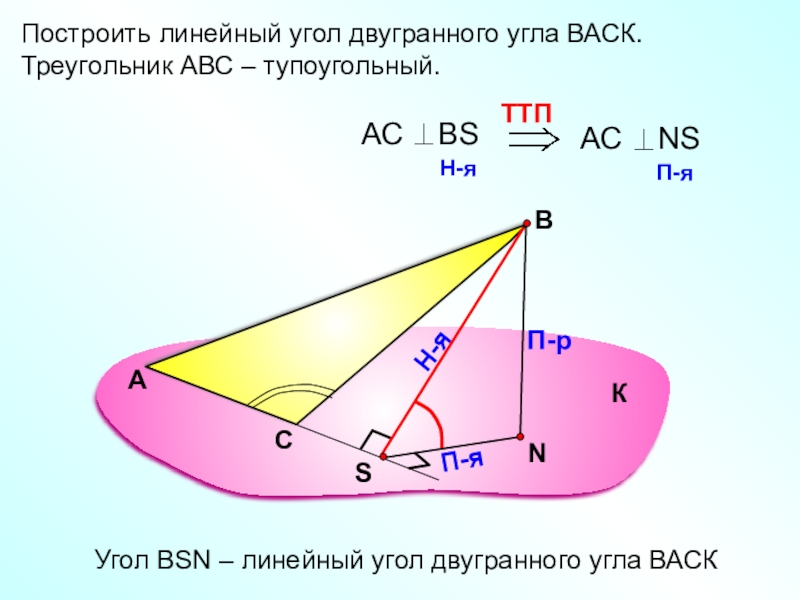
- 16. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – тупоугольный.АВП-рН-яП-яУгол ВSN – линейный угол двугранного угла ВАСККС
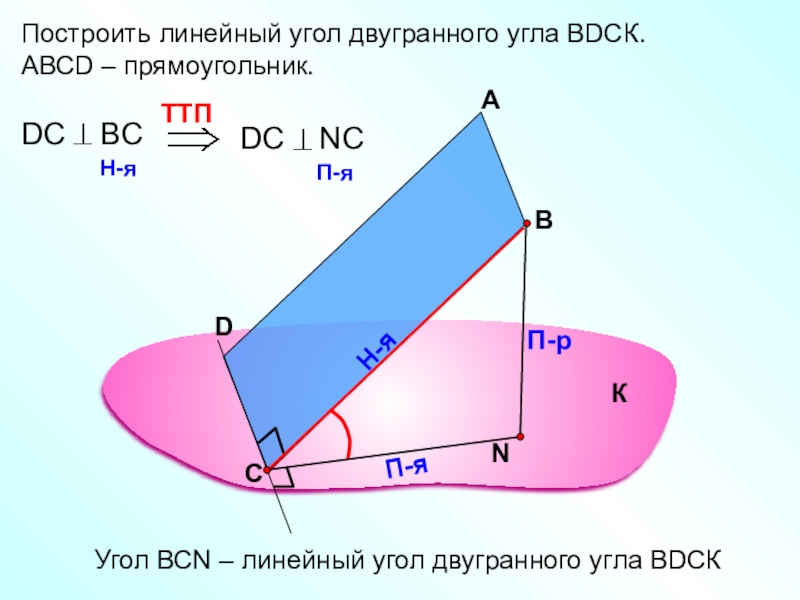
- 17. Построить линейный угол двугранного угла ВDСК.АВСD – прямоугольник.АВП-рН-яП-яУгол ВСN – линейный угол двугранного угла ВDСККСD
- 18. Построить линейный угол двугранного угла ВDСК.АВСD –
- 19. Построить линейный угол двугранного угла ВDСК.АВСD –
- 20. Построить линейный угол двугранного угла ВDСК.АВСD –
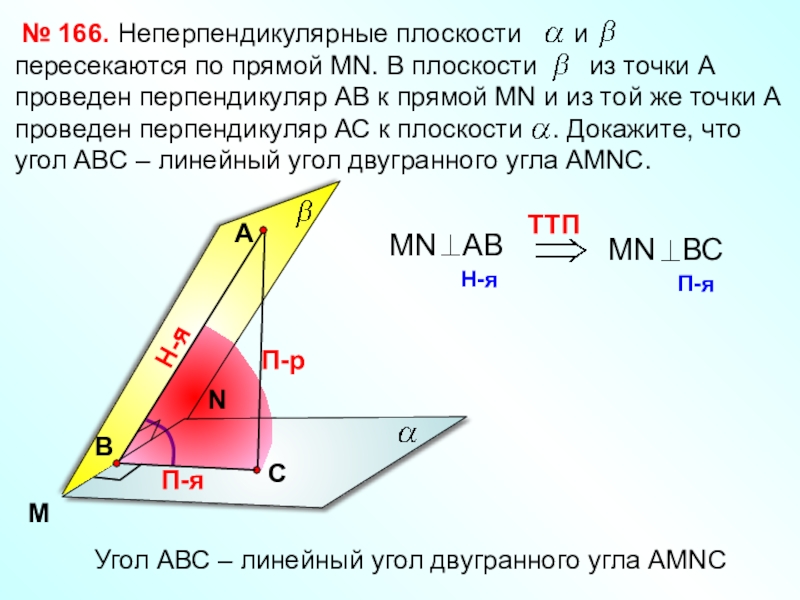
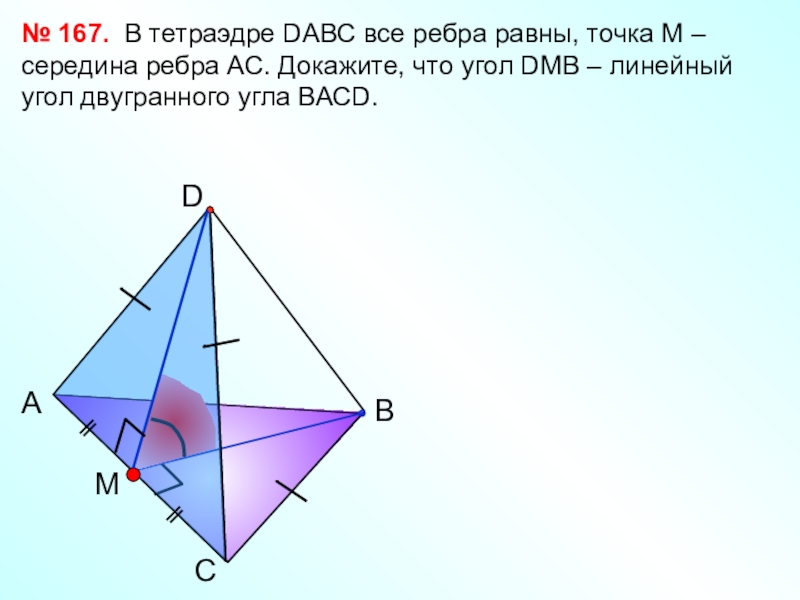
- 21. № 166.MNАП-рН-яП-яУгол АВС – линейный угол двугранного угла АМNC
- 22. САВDM
- 23. Слайд 23
- 24. Слайд 24
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки А на прямую.aАРасстояние от точки до плоскости – длина перпендикуляраПовторениеА
Слайд 2
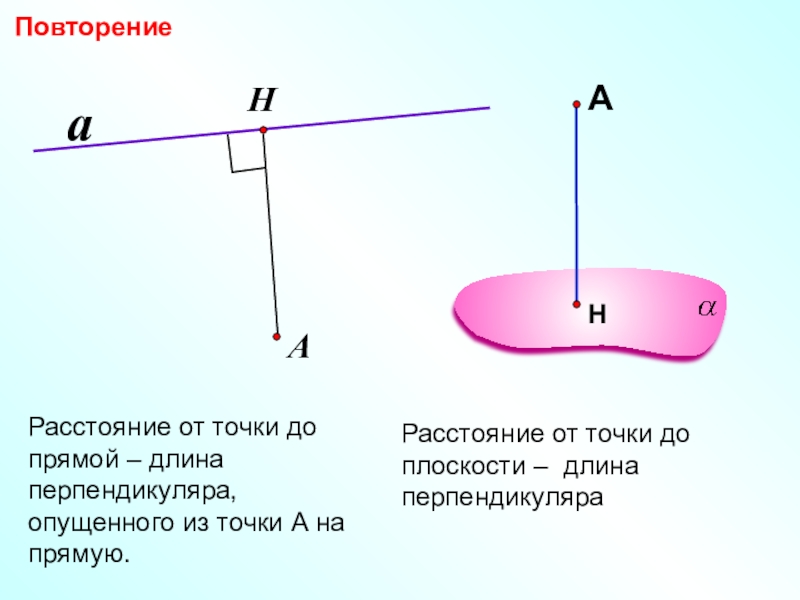
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки
А на прямую.
a
А
Расстояние от точки до плоскости – длина перпендикуляра
Повторение
А
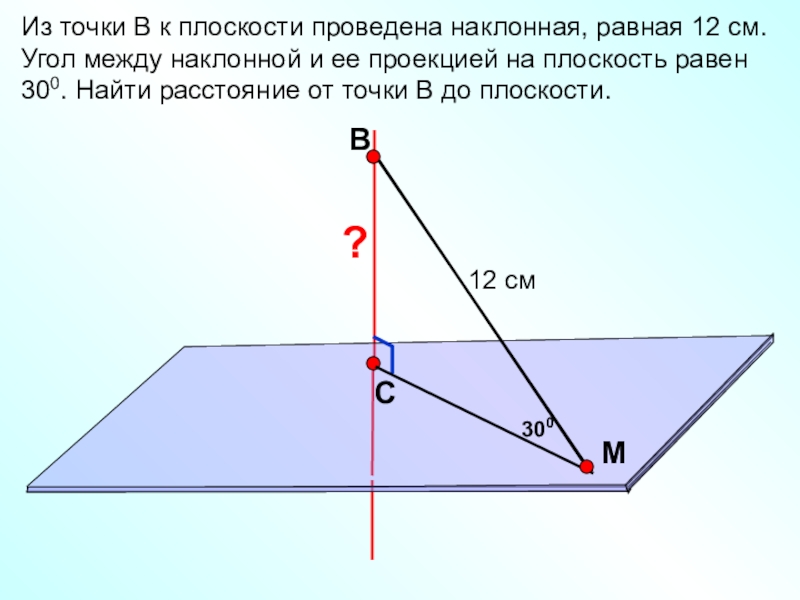
Слайд 3В
С
M
Из точки В к плоскости проведена наклонная, равная 12 см. Угол
между наклонной и ее проекцией на плоскость равен 300. Найти расстояние от точки В до плоскости.
12 см
300
?
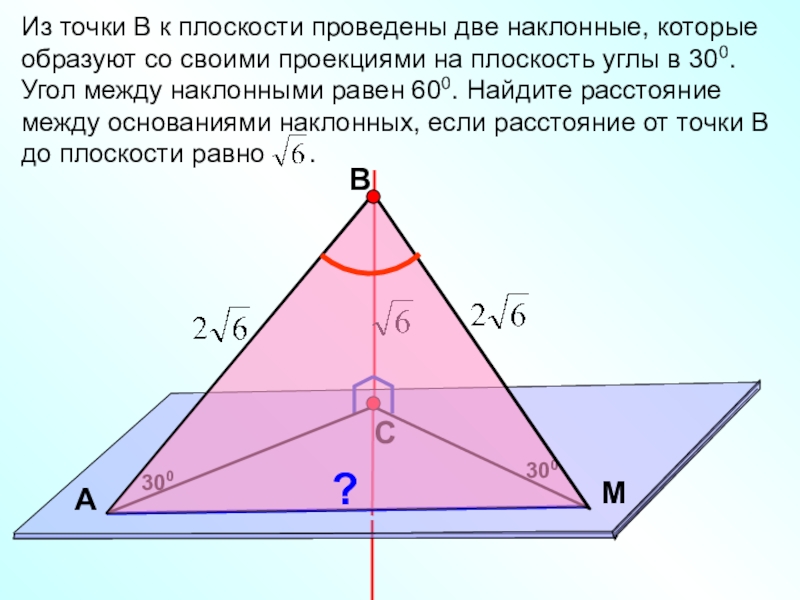
Слайд 4В
С
M
А
Из точки В к плоскости проведены две наклонные, которые образуют со
своими проекциями на плоскость углы в 300. Угол между наклонными равен 600. Найдите расстояние между основаниями наклонных, если расстояние от точки В до плоскости равно .
300
300
?
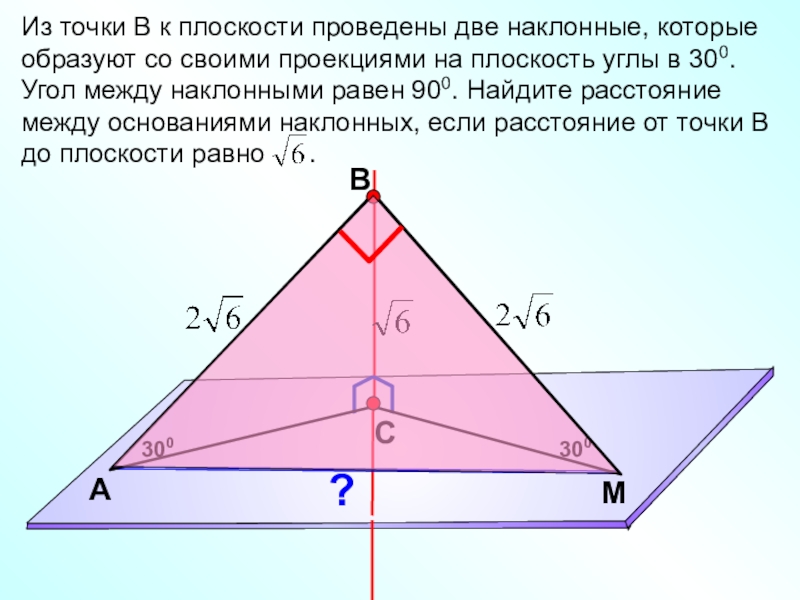
Слайд 5В
С
M
А
Из точки В к плоскости проведены две наклонные, которые образуют со
своими проекциями на плоскость углы в 300. Угол между наклонными равен 900. Найдите расстояние между основаниями наклонных, если расстояние от точки В до плоскости равно .
300
300
?
Слайд 6В
С
M
А
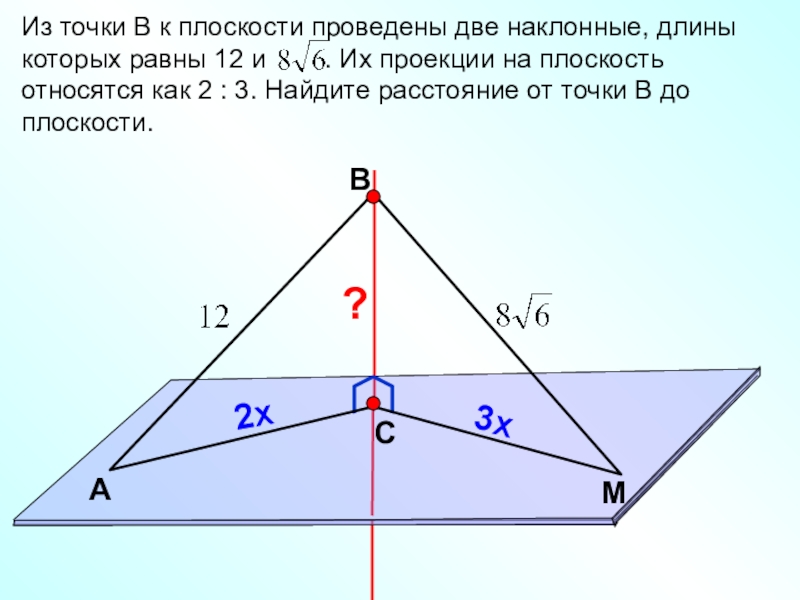
Из точки В к плоскости проведены две наклонные, длины
которых равны 12
и . Их проекции на плоскость относятся как 2 : 3. Найдите расстояние от точки В до плоскости.
?
2х
3х
Слайд 7
П-я
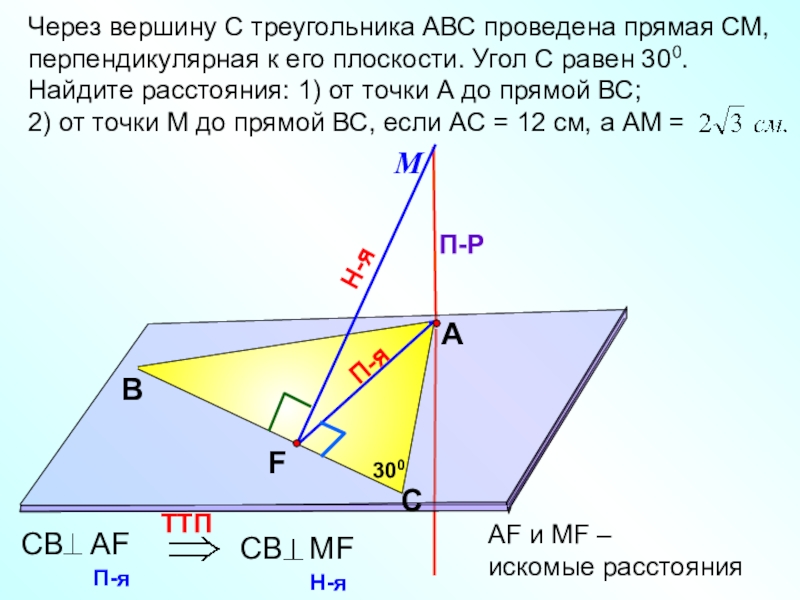
Через вершину С треугольника АВС проведена прямая СМ, перпендикулярная к
его плоскости. Угол С равен 300. Найдите расстояния: 1) от точки А до прямой ВС;
2) от точки М до прямой ВС, если АС = 12 см, а АМ =
2) от точки М до прямой ВС, если АС = 12 см, а АМ =
А
В
С
П-Р
Н-я
АF и МF –
искомые расстояния
300
Слайд 8
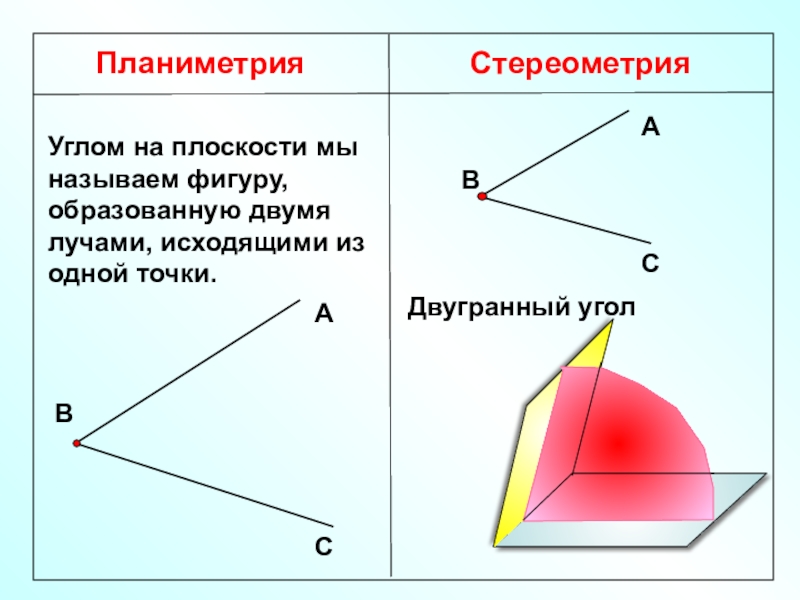
Планиметрия
Стереометрия
Углом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из
одной точки.
Двугранный угол
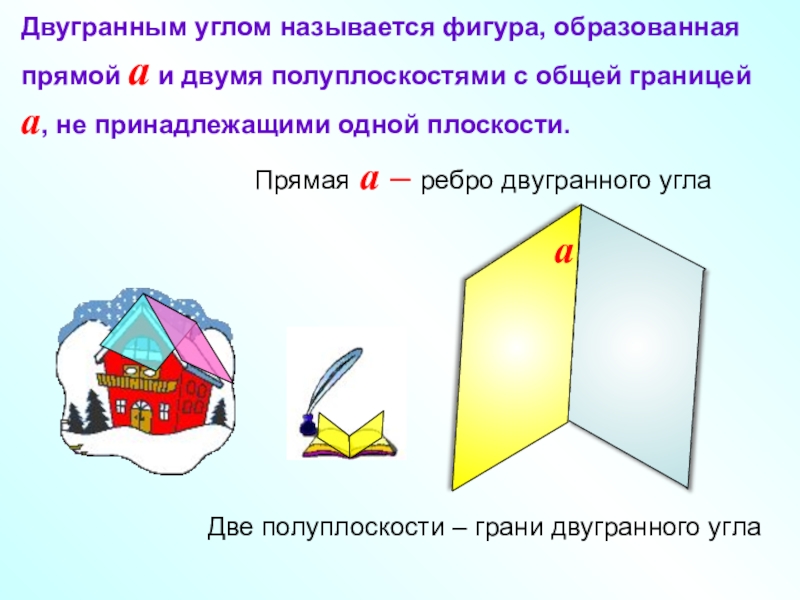
Слайд 9Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с
общей границей a, не принадлежащими одной плоскости.
Две полуплоскости – грани двугранного угла
Прямая a – ребро двугранного угла
a
Слайд 10
Угол РDEK
Двугранный угол АВNМ, где ВN – ребро, точки А
и М лежат в гранях двугранного угла
А
В
N
Р
M
К
D
E
Угол SFX – линейный угол двугранного угла
Слайд 11
Угол РОК – линейный угол двугранного угла РDEК.
D
E
Градусной мерой двугранного угла
называется градусная мера его линейного угла.
Алгоритм построения линейного угла.
Слайд 12
Все линейные углы двугранного угла равны друг другу.
1
Лучи ОА и О1А1
– сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы АОВ и А1О1В1 равны,
как углы с сонаправленными сторонами
Слайд 14
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
А
С
В
П-р
Н-я
П-я
Угол ВMN –
линейный угол двугранного угла ВАСК
К
Слайд 15
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
А
В
П-р
Н-я
П-я
Угол ВСN –
линейный угол двугранного угла ВАСК
К
С
Слайд 16
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
А
В
П-р
Н-я
П-я
Угол ВSN –
линейный угол двугранного угла ВАСК
К
С
Слайд 17
Построить линейный угол двугранного угла ВDСК.
АВСD – прямоугольник.
А
В
П-р
Н-я
П-я
Угол ВСN – линейный
угол двугранного угла ВDСК
К
С
D
Слайд 18
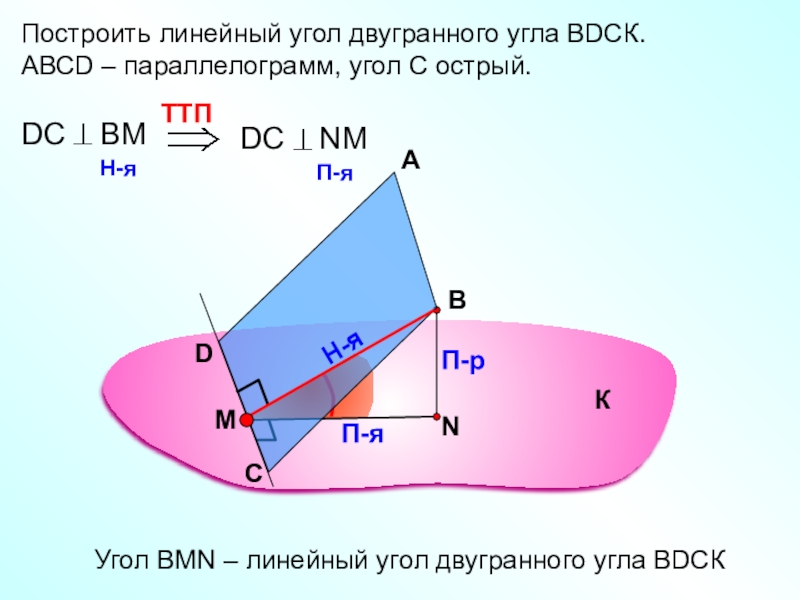
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С острый.
А
В
П-р
П-я
Угол
ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
Слайд 19
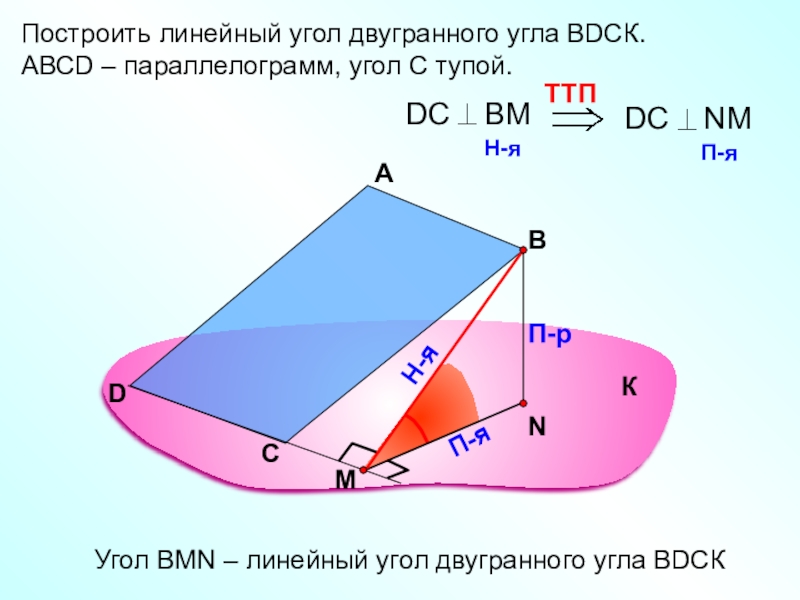
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С тупой.
А
В
П-р
П-я
Угол
ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
Слайд 20
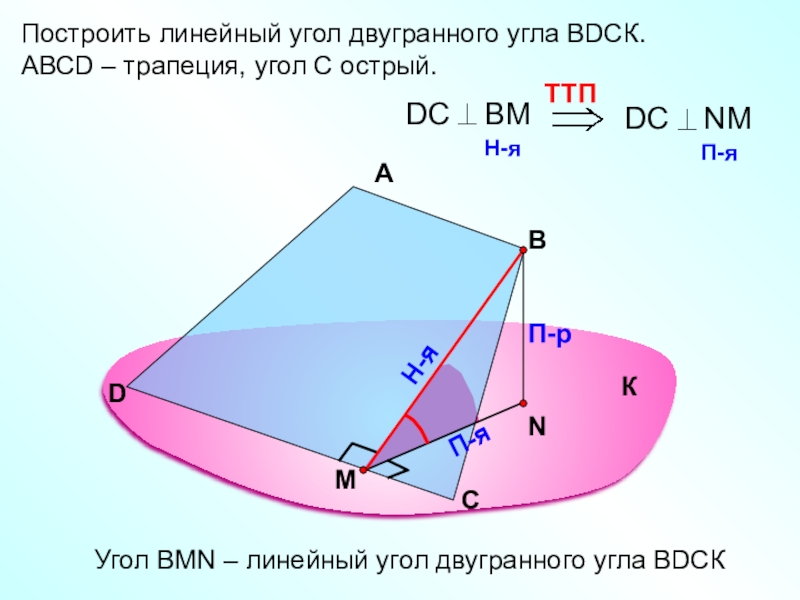
Построить линейный угол двугранного угла ВDСК.
АВСD – трапеция, угол С острый.
А
В
П-р
П-я
Угол
ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
Слайд 22
С
А
В
D
M
В тетраэдре DАВС все
ребра равны, точка М – середина ребра АС. Докажите, что угол DМВ – линейный угол двугранного угла ВАСD.
№ 167.
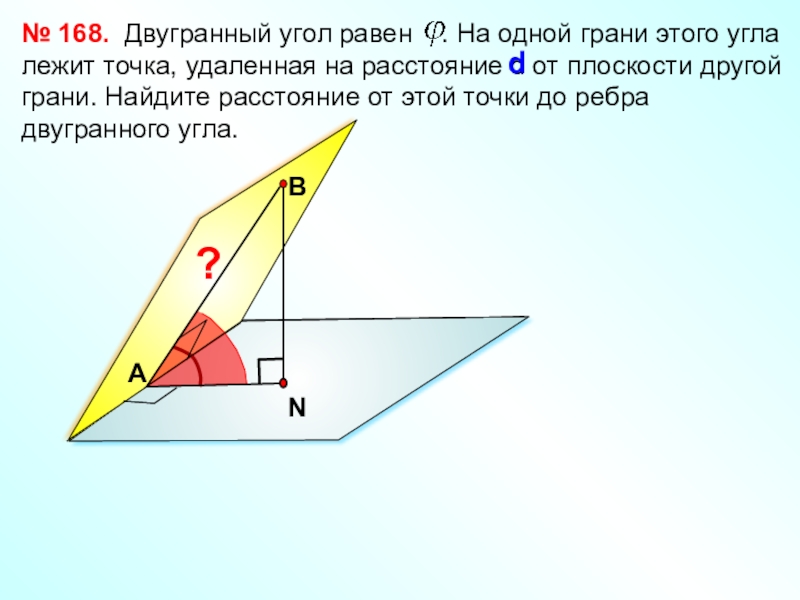
Слайд 23 Двугранный угол равен
. На одной грани этого угла лежит точка, удаленная на расстояние d от плоскости другой грани. Найдите расстояние от этой точки до ребра двугранного угла.
№ 168.
В
d
А
?
Слайд 24
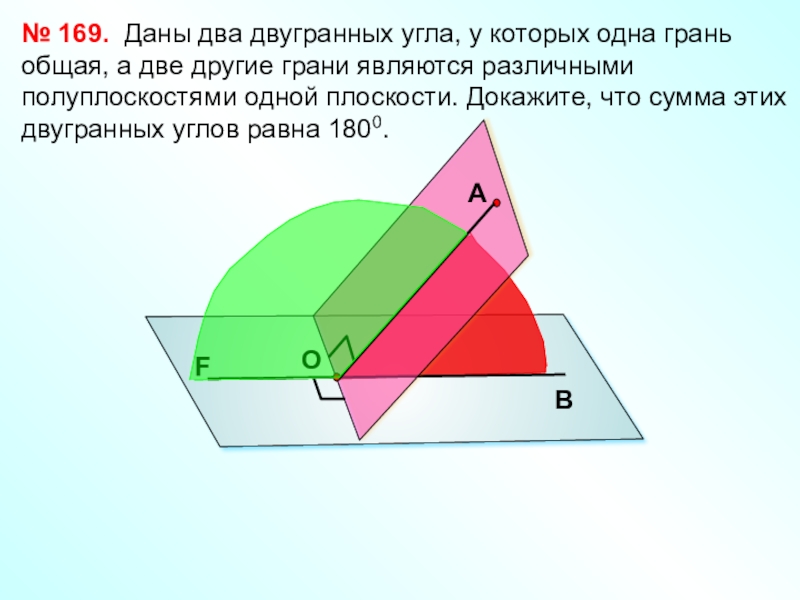
Даны два двугранных угла,
у которых одна грань общая, а две другие грани являются различными полуплоскостями одной плоскости. Докажите, что сумма этих двугранных углов равна 1800.
№ 169.
А
