- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку 7 класс. Геометрия Параллельные прямые
Содержание
- 1. Презентация к уроку 7 класс. Геометрия Параллельные прямые
- 2. План1.Параллельные прямые в начертательной геометрии2.Геометрия Евклида и Лобачевского3.Итоги4.Список литературы
- 3. На параллельность прямых в разные времена у ученых были различные взгляды.
- 4. 1.Параллельные прямые в начертательной геометрииЕсли в пространстве
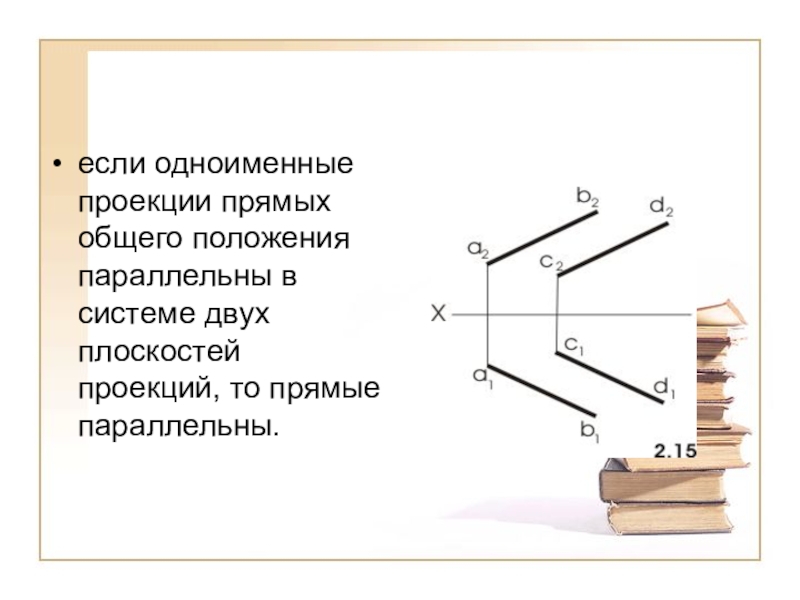
- 5. если одноименные проекции прямых общего положения параллельны в системе двух плоскостей проекций, то прямые параллельны.
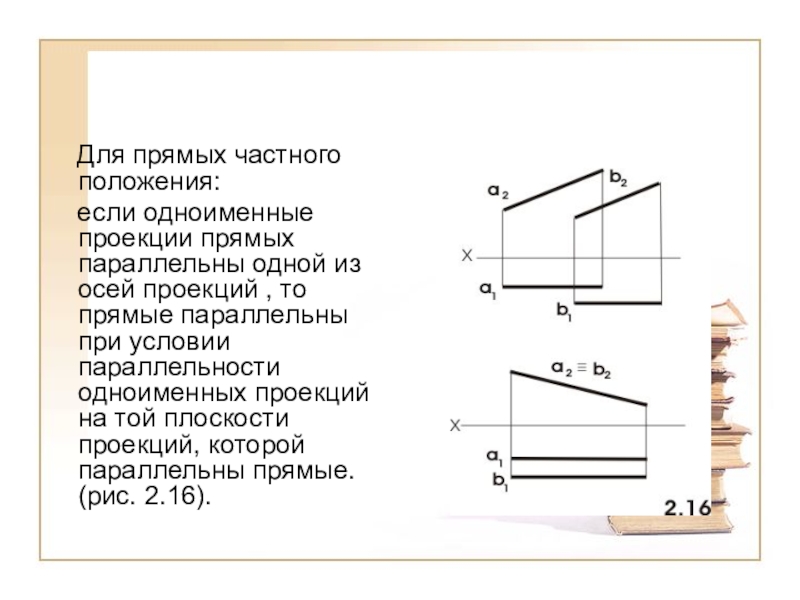
- 6. Для прямых частного положения:
- 7. 2.Геометрия Евклида и Лобачевского Существуют два
- 8. В евклидовой геометрии, параллельные прямые
- 9. В геометрии Лобачевского, великий ученый
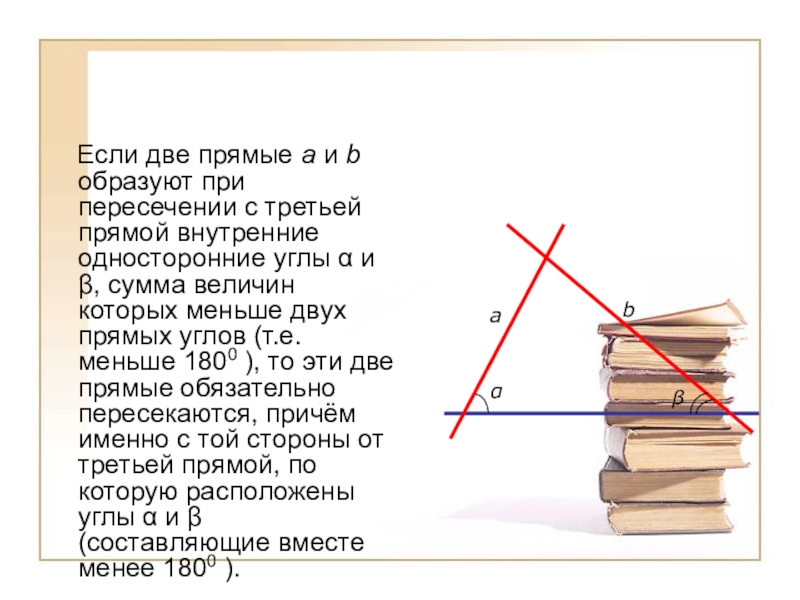
- 10. Если две прямые a и
- 11. Данное утверждение заметно сложнее остальных
- 12. Сложность формулировки пятого постулата и
- 13. Николай Иванович Лобачевский родился
- 14. Стараясь исключить пятый постулат Евклида
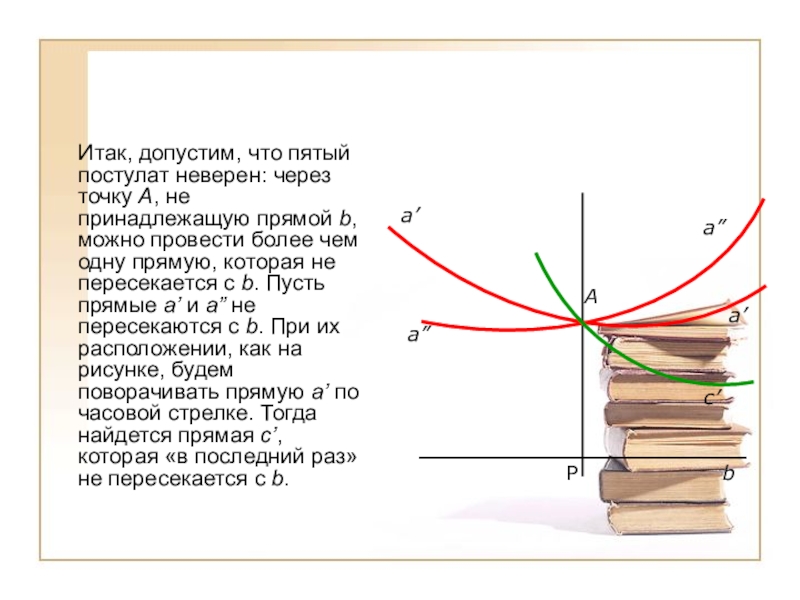
- 15. Итак, допустим, что пятый
- 16. Значит, прямые, получающиеся из
- 17. Лобачевский называет прямые c’ и
- 18. Лобачевский доказывает, что две параллельные
- 19. А в свою очередь две
- 20. В своих доказательствах Лобачевский надеялся
- 21. Тогда русский математик рассматривает две
- 22. Длина перпендикуляра непрерывно возрастает при
- 23. Построив прямую с1 , симметричную
- 24. То есть возникает своеобразный «бесконечный треугольник»: у
- 25. Это уже никак не согласовалось
- 26. 3.Итоги После долгих трудов Лобачевский наконец
- 27. Иначе говоря, если мы добавляем
- 28. С докладом об открытии неевклидовой
- 29. 4.Список литературыЭнциклопедия для детей. Т.11. Математика. Главный
План1.Параллельные прямые в начертательной геометрии2.Геометрия Евклида и Лобачевского3.Итоги4.Список литературы
Слайд 2План
1.Параллельные прямые в начертательной геометрии
2.Геометрия Евклида и Лобачевского
3.Итоги
4.Список литературы
Слайд 41.Параллельные прямые в начертательной геометрии
Если в пространстве прямые параллельны, то их
одноименные проекции параллельны между собой. Действительно, проецирующие плоскости R и Q, проведенные через параллельные прямые АВ и СD, параллельны между собой. С плоскостью проекций П 1 они пересекаются по параллельным прямым a1 b1 и с1d1 - проекциям прямых АВ и СD на плоскости П1. Однако из параллельности проекций не всегда следует параллельность прямых. Для прямых общего положения условия параллельности следующие:
Слайд 5
если одноименные проекции прямых общего положения параллельны в системе двух плоскостей
проекций, то прямые параллельны.
Слайд 6
Для прямых частного положения:
если одноименные проекции прямых
параллельны одной из осей проекций , то прямые параллельны при условии параллельности одноименных проекций на той плоскости проекций, которой параллельны прямые. (рис. 2.16).
Слайд 72.Геометрия Евклида и Лобачевского
Существуют два основных взгляда на параллельность
прямых. Они выражены в Евклидовой геометрии, а так же в геометрии Лобачевского.
Слайд 8
В евклидовой геометрии, параллельные прямые – это прямые, которые
лежат в одной плоскости либо совпадают, либо не пересекаются.
Слайд 9
В геометрии Лобачевского, великий ученый оспаривает пятый постулат евклидовых
«Начал». Вот как звучит пятый постулат:
Слайд 10
Если две прямые a и b образуют при пересечении
с третьей прямой внутренние односторонние углы α и β, сумма величин которых меньше двух прямых углов (т.е. меньше 1800 ), то эти две прямые обязательно пересекаются, причём именно с той стороны от третьей прямой, по которую расположены углы α и β (составляющие вместе менее 1800 ).
a
b
α
β
Слайд 11
Данное утверждение заметно сложнее остальных аксиом. Поэтому в современных
учебниках его обычно заменяют на равносильную аксиому параллельности: к данной прямой через данную вне её точку можно провести не более одной параллельной прямой.
Слайд 12
Сложность формулировки пятого постулата и его неубедительность привели к
тому, что очень многие математики жившие после Евклида, старались исключить этот постулат из списка аксиом, то есть доказать его как теорему с помощью остальных аксиом Евклида. Дальше всего на этом поприще продвинулся Николай Иванович Лобачевский.
Слайд 13
Николай Иванович Лобачевский родился 1 декабря (20 ноября)
1792 года в Нижнем Новгороде в бедной семье мелкого чиновника. Лобачевский - автор ряда работ по математическому анализу, механике, физике и др. Он первым в России опубликовал курс высшей алгебры. Идеи Лобачевского повлияли на развитие русского авангарда - творчество В. Хлебникова, К. Малевича и др.
Слайд 14
Стараясь исключить пятый постулат Евклида Лобачевский допустил, что он
неверен, а остальные аксиомы справедливы, то есть рано или поздно надеялся прийти к противоречию.
Слайд 15
Итак, допустим, что пятый постулат неверен: через точку
А, не принадлежащую прямой b, можно провести более чем одну прямую, которая не пересекается с b. Пусть прямые a’ и a” не пересекаются с b. При их расположении, как на рисунке, будем поворачивать прямую a’ по часовой стрелке. Тогда найдется прямая с’, которая «в последний раз» не пересекается с b.
a”
a”
a’
a’
c’
P
b
А
Слайд 16
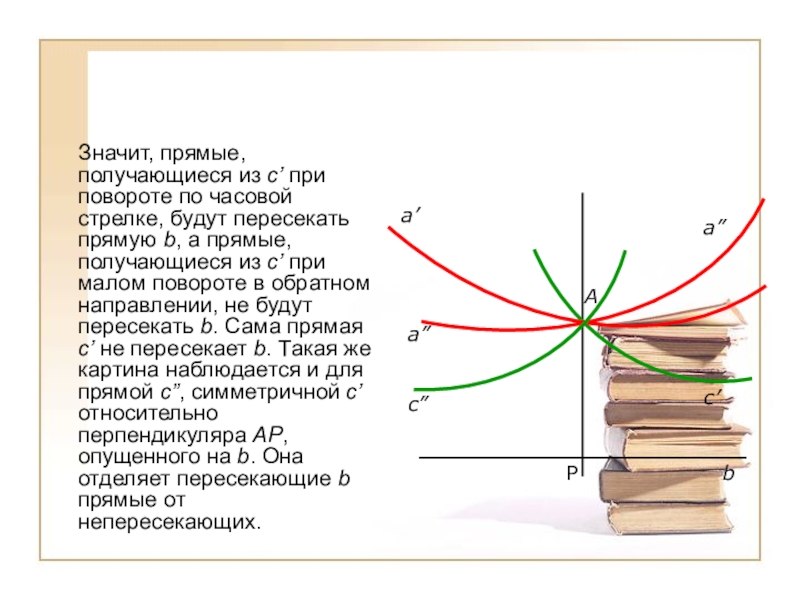
Значит, прямые, получающиеся из c’ при повороте по
часовой стрелке, будут пересекать прямую b, а прямые, получающиеся из c’ при малом повороте в обратном направлении, не будут пересекать b. Сама прямая c’ не пересекает b. Такая же картина наблюдается и для прямой c”, симметричной c’ относительно перпендикуляра AP, опущенного на b. Она отделяет пересекающие b прямые от непересекающих.
a”
a”
a’
c’
P
b
c”
А
Слайд 17
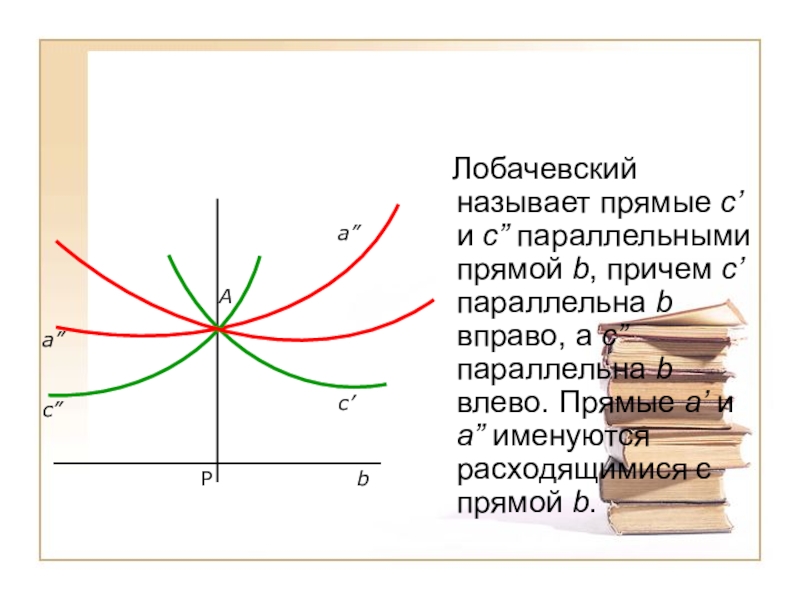
Лобачевский называет прямые c’ и c” параллельными прямой b,
причем c’ параллельна b вправо, а с” параллельна b влево. Прямые a’ и a” именуются расходящимися с прямой b.
a”
a”
c’
P
b
c”
А
Слайд 18
Лобачевский доказывает, что две параллельные прямые неограниченно сближаются друг
с другом в сторону параллельности, но в обратном направлении они неограниченно удаляются друг от друга.
a
b
Слайд 19
А в свою очередь две расходящиеся прямые имеют единственный
общий перпендикуляр, по обе стороны от которого они неограниченно удаляются друг от друга
a
b
c
Слайд 20
В своих доказательствах Лобачевский надеялся найти противоречие и исключить
пятый постулат Евклида. Однако противоречия в них не было.
Слайд 21
Тогда русский математик рассматривает две параллельные прямые b и
c и берет на прямой b движущуюся точку М, удаляющуюся в сторону, обратную параллельности. В каждом положении точки М он выстраивает перпендикуляр p к прямой b до его пересечения с прямой с.
c
M1
M2
M3
b
Слайд 22
Длина перпендикуляра непрерывно возрастает при движении точки М, и,
когда она попадает в некоторое положение Q, длина перпендикуляра становится бесконечной. То есть перпендикуляр p в точке Q параллелен прямой c.
M1
M2
M3
Q
c
b
Слайд 23
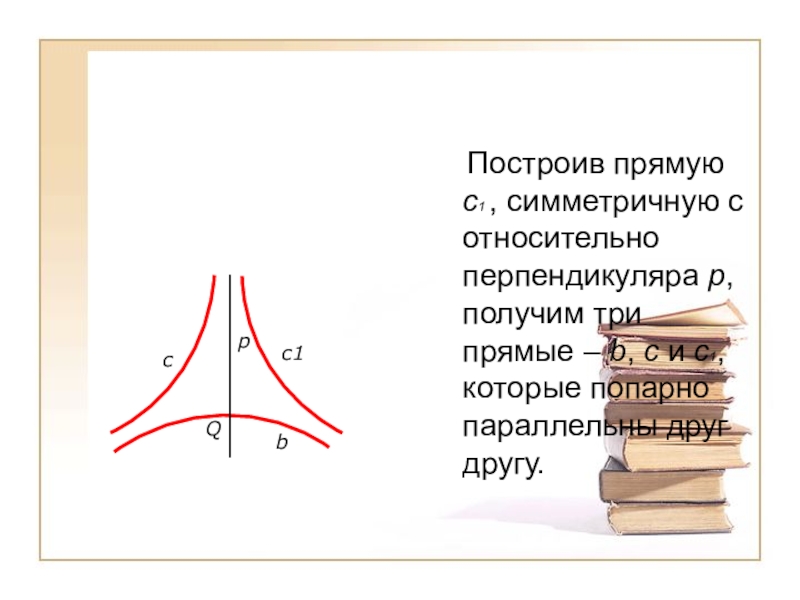
Построив прямую с1 , симметричную с относительно перпендикуляра p,
получим три прямые – b, c и c1, которые попарно параллельны друг другу.
c1
c
b
Q
p
Слайд 24
То есть возникает своеобразный «бесконечный треугольник»: у него каждые две стороны
параллельны друг другу, а вершин совсем нет (они находятся в бесконечности).
c1
c
b
Q
p
Слайд 25
Это уже никак не согласовалось с привычными представлениями о
расположении прямых линий. Однако никакого противоречия и здесь не наблюдалось.
Слайд 263.Итоги
После долгих трудов Лобачевский наконец то понимает, что в
пятом постулате Евклида противоречия быть не может.
Слайд 27
Иначе говоря, если мы добавляем ко всем прочим аксиомам
ещё и пятый постулат, то получается непротиворечивая геометрическая система – та евклидова геометрия, к которой мы так привыкли. Если же ко всем прочим аксиомам вместо пятого постулата мы добавим отрицание аксиомы параллельности, то получим другую геометрическую систему (Лобачевский назвал её «воображаемой» геометрией), которая, однако, тоже непротиворечива.
Слайд 28
С докладом об открытии неевклидовой геометрии Лобачевский выступил в
1824 г., но поддержки не нашел. Математики его времени еще не были подготовлены к мысли о возможности существование иной, неевклидовой геометрии. Учёный умер, так и не добившись признания своих идей.
Слайд 294.Список литературы
Энциклопедия для детей. Т.11. Математика. Главный редактор М.Д. Аксенова.- М:Аванта+,1999.-688с.:
ил.
Математика: Школьная энциклопедия. Гл. ред. С. М. Никольский. – М.: Большая Российская энциклопедия; Дрофа, 2007. – 527 с.: ил.
Савин А. П. Энциклопедический словарь юного математика. – М.: Педагогика, 2009 – 352 с.: ил.
Математика: Школьная энциклопедия. Гл. ред. С. М. Никольский. – М.: Большая Российская энциклопедия; Дрофа, 2007. – 527 с.: ил.
Савин А. П. Энциклопедический словарь юного математика. – М.: Педагогика, 2009 – 352 с.: ил.