- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к урокам математики Магические квадраты 7-9 классы
Содержание
- 1. Презентация к урокам математики Магические квадраты 7-9 классы
- 2. Введение Великие ученые древности считали количественные
- 3. Некоторые выдающиеся математики посвятили свои
- 4. Магические квадраты Полного описания всех
- 5. Расположить натуральные числа от 1 до
- 6. Возможные варианты:
- 7. В магическом квадрате 3 на
- 8. Рассмотрим число 9. Оно
- 9. Какое из этих двух чисел окажется
- 10. Такой магический квадрат был у древних
Введение Великие ученые древности считали количественные отношения основой сущности мира. «В дни моей юности я в свободное время развлекался тем, что составлял… магические квадраты» Бенджамин Франклин. Магический квадрат- это квадрат, сумма чисел которого в каждом
Слайд 2Введение
Великие ученые древности считали количественные отношения основой сущности мира.
«В дни моей юности я в свободное время развлекался тем, что составлял… магические квадраты»
Бенджамин Франклин.
Магический квадрат- это квадрат, сумма чисел которого в каждом горизонтальном ряду, в каждом вертикальном ряду и по каждой из диагоналей одна и та же.
Слайд 3 Некоторые выдающиеся математики посвятили свои работы магическим квадратам и
полученные ими результаты оказали влияние на развитие латинских квадратов, определителей, разбиений, матриц, сравнений и других нетривиальных разделов математики. Цель настоящей работы – знакомство с различными магическими квадратами и изучение областей их применения.
Слайд 4Магические квадраты
Полного описания всех возможных магических квадратов не
получено и до сего времени. Магических квадратов 2 на 2 не существует. Существует единственный магический квадрат 3 на 3 ,так как остальные магические квадраты 3 на 3 получаются из него либо поворотом вокруг центра, либо отражением относительно одной из его осей симметрии.
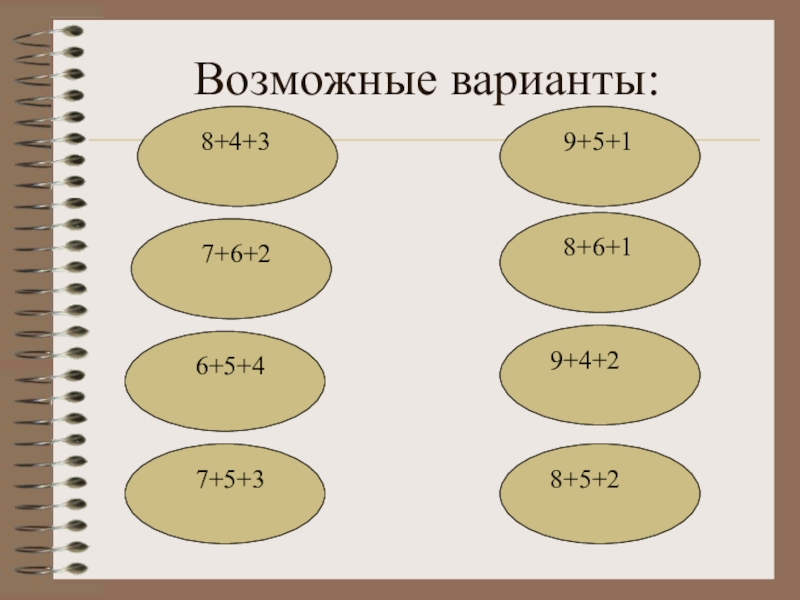
Слайд 5 Расположить натуральные числа от 1 до 9 в магический квадрат
3 на 3 можно 8 различными способами:
Слайд 7 В магическом квадрате 3 на 3 магической постоянной 15
должны быть равны суммы трех чисел по 8 направлениям: по 3 строкам, 3 столбцам и 2 диагоналям.
Так как число, стоящее в центре, принадлежит 1 строке, 1 столбцу и 2 диагоналям, оно входит в 4 из 8 троек, дающих в сумме магическую постоянную. Такое число только одно: это 5. Следовательно, число, стоящее в центре магического квадрата 3 на 3, уже известно: оно равно 5.
Так как число, стоящее в центре, принадлежит 1 строке, 1 столбцу и 2 диагоналям, оно входит в 4 из 8 троек, дающих в сумме магическую постоянную. Такое число только одно: это 5. Следовательно, число, стоящее в центре магического квадрата 3 на 3, уже известно: оно равно 5.
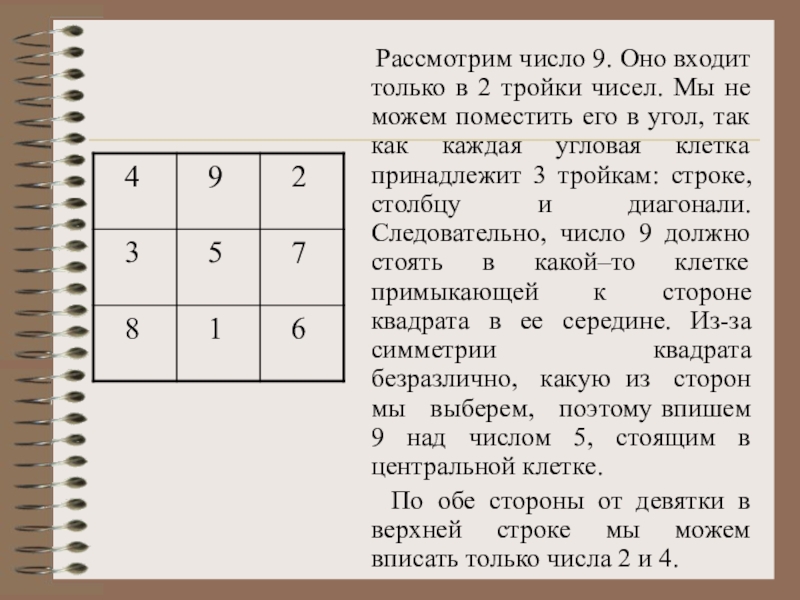
Слайд 8 Рассмотрим число 9. Оно входит только в 2
тройки чисел. Мы не можем поместить его в угол, так как каждая угловая клетка принадлежит 3 тройкам: строке, столбцу и диагонали. Следовательно, число 9 должно стоять в какой–то клетке примыкающей к стороне квадрата в ее середине. Из-за симметрии квадрата безразлично, какую из сторон мы выберем, поэтому впишем 9 над числом 5, стоящим в центральной клетке.
По обе стороны от девятки в верхней строке мы можем вписать только числа 2 и 4.
По обе стороны от девятки в верхней строке мы можем вписать только числа 2 и 4.
Слайд 9 Какое из этих двух чисел окажется в правом верхнем углу
и какое в левом, опять – таки не имеет значения, так как одно расположение чисел переходит в другое при зеркальном отражении. Остальные клетки заполняются автоматически. Проведенное нами простое построение магического квадрата 3 на 3 доказывает его единственность.
Слайд 10 Такой магический квадрат был у древних китайцев символом огромного значения.
Цифра 5 в середине означала землю, а вокруг нее в строгом равновесии располагались огонь (2 и 7), вода (1 и 6),дерево (3 и 8), металл (4 и 9).
С увеличением размеров квадрата (числа клеток) быстро растет количество возможных магических квадратов такого размера. Существует 880 магических квадратов порядка 4 и 275 305 224 магических квадратов порядка 5. Причем, квадраты 5 на 5 были известны еще в средние века.
С увеличением размеров квадрата (числа клеток) быстро растет количество возможных магических квадратов такого размера. Существует 880 магических квадратов порядка 4 и 275 305 224 магических квадратов порядка 5. Причем, квадраты 5 на 5 были известны еще в средние века.