- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к открытому уроку
Содержание
- 1. Презентация к открытому уроку
- 2. Историческая справкаПифагор – древнегреческий ученый, живший в
- 3. С именем Пифагора связано
- 4. Опорное повторение по готовым чертежамКакой треугольник изображён?
- 5. На какие два многоугольника разбит данный многоугольник
- 6. Практическая работа Постройте в тетрадях
- 7. Теорема Пифагора В прямоугольном треугольнике квадрат
- 8. Стихотворение о теореме ПифагораЕсли дан нам треугольник,И
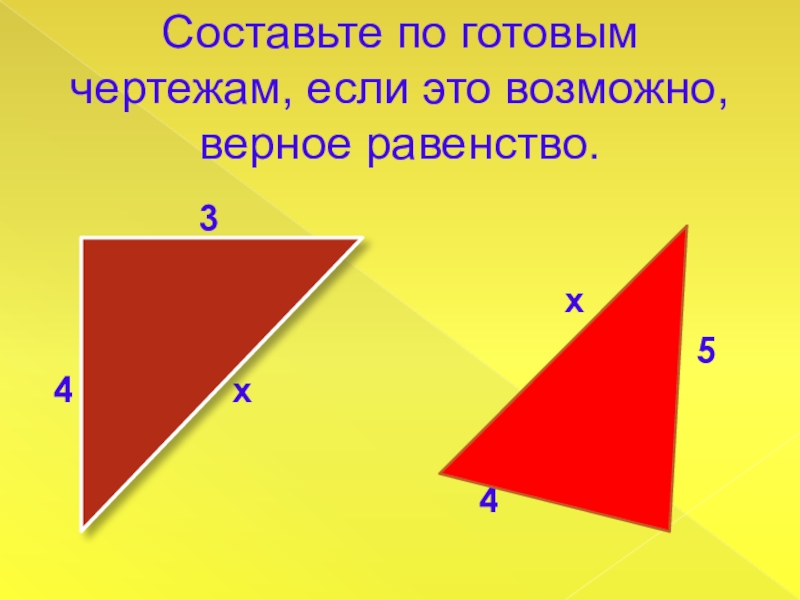
- 9. Составьте по готовым чертежам, если это возможно,
- 10. РЕШЕНИЕ ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ
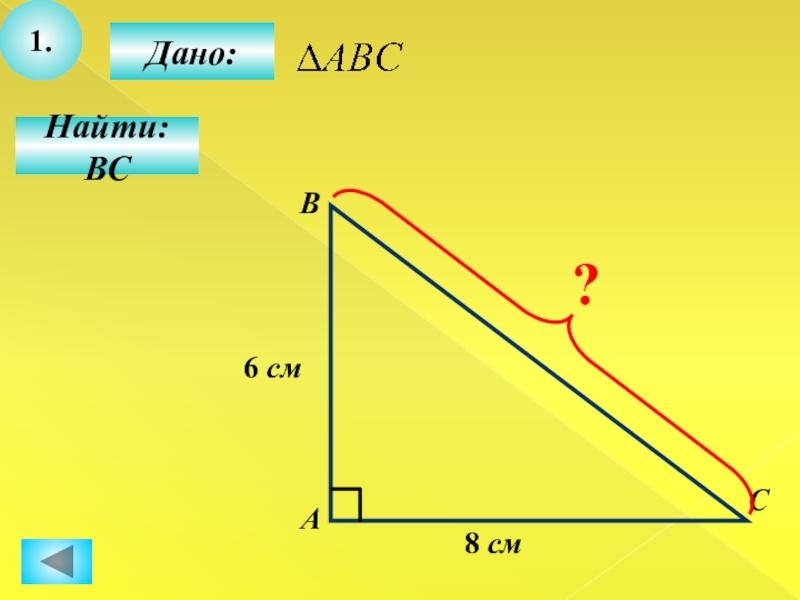
- 11. 1.Найти: ВССВАДано:8 см6 см?
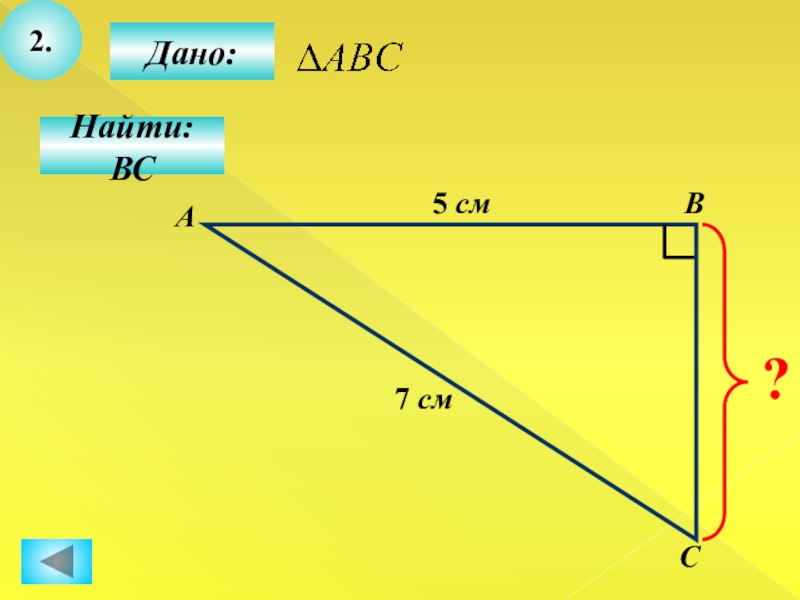
- 12. 2.Дано:СВНайти: ВСА5 см7 см?
- 13. 3.Дано:Найти:АBCD?12 см13 см
- 14. Подведение итоговВозможно ли было решение задач данного
- 15. 4. В Древнем Египте был известен треугольник
- 16. Домашнее заданиеП. 54. № 483 (б,в);
Историческая справкаПифагор – древнегреческий ученый, живший в VI веке до нашей эры. Вообще надо заметить, что о жизни и деятельности Пифагора, который умер две с половиной тысячи лет тому назад, нет достоверных сведений. Биографию
Слайд 2Историческая справка
Пифагор – древнегреческий ученый, живший в VI веке до нашей
эры.
Вообще надо заметить, что о жизни и деятельности Пифагора, который умер две с половиной тысячи лет тому назад, нет достоверных сведений. Биографию учёного и его труды приходится реконструировать по произведениям других античных авторов, а они часто противоречат друг другу.
Вообще надо заметить, что о жизни и деятельности Пифагора, который умер две с половиной тысячи лет тому назад, нет достоверных сведений. Биографию учёного и его труды приходится реконструировать по произведениям других античных авторов, а они часто противоречат друг другу.
Слайд 3 С именем Пифагора связано много важных научных открытий:
в географии и астрономии – представление о том, что Земля – шар и что существуют другие, похожие на неё миры; в музыке – зависимость между длиной струны арфы и звуком, который она издаёт; в геометрии – построение правильных многоугольников (один из них пятиконечная звезда – стал символом пифагорейцев).
Венчала геометрию теорема Пифагора, которой посвящён сегодняшний урок.
Но изучение вавилонских клинописных таблиц и древних китайских рукописей показало, что это утверждение было известно задолго до Пифагора. Заслуга же Пифагора состояла в том, что он открыл доказательство этой теоремы.
Венчала геометрию теорема Пифагора, которой посвящён сегодняшний урок.
Но изучение вавилонских клинописных таблиц и древних китайских рукописей показало, что это утверждение было известно задолго до Пифагора. Заслуга же Пифагора состояла в том, что он открыл доказательство этой теоремы.
Слайд 4Опорное повторение по готовым чертежам
Какой треугольник изображён?
(Определите его
вид)
Назовите катеты и гипотенузу данного треугольника.
Как найти площадь
Δ АВС?
Назовите катеты и гипотенузу данного треугольника.
Как найти площадь
Δ АВС?
В
А
С
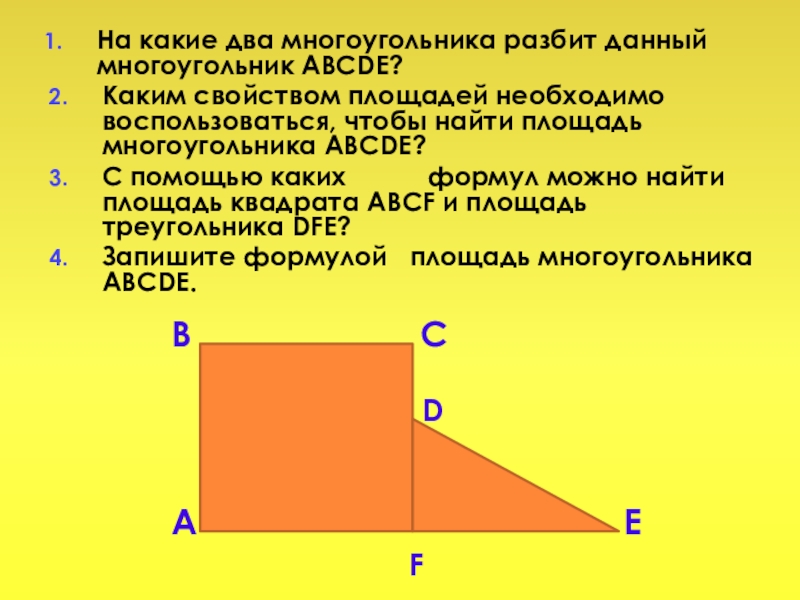
Слайд 5На какие два многоугольника разбит данный многоугольник ABCDE?
Каким свойством площадей необходимо
воспользоваться, чтобы найти площадь многоугольника ABCDE?
С помощью каких формул можно найти площадь квадрата ABCF и площадь треугольника DFE?
Запишите формулой площадь многоугольника ABCDE.
С помощью каких формул можно найти площадь квадрата ABCF и площадь треугольника DFE?
Запишите формулой площадь многоугольника ABCDE.
В С
D
A E
F
Слайд 6
Практическая работа
Постройте в тетрадях прямоугольный треугольник (с катетами, длина которых
для удобства выражается целыми числами).
Измерьте катеты и гипотенузу. Результаты измерений запишите в тетрадях.
Возведите все результаты в квадрат, т. е. Узнайте величины a2; b2; c2.
Сложите квадраты катетов (a2 + b2) и сравните с квадратом гипотенузы.
У всех ли получилось, что a2 + b2 = с2?
Измерьте катеты и гипотенузу. Результаты измерений запишите в тетрадях.
Возведите все результаты в квадрат, т. е. Узнайте величины a2; b2; c2.
Сложите квадраты катетов (a2 + b2) и сравните с квадратом гипотенузы.
У всех ли получилось, что a2 + b2 = с2?
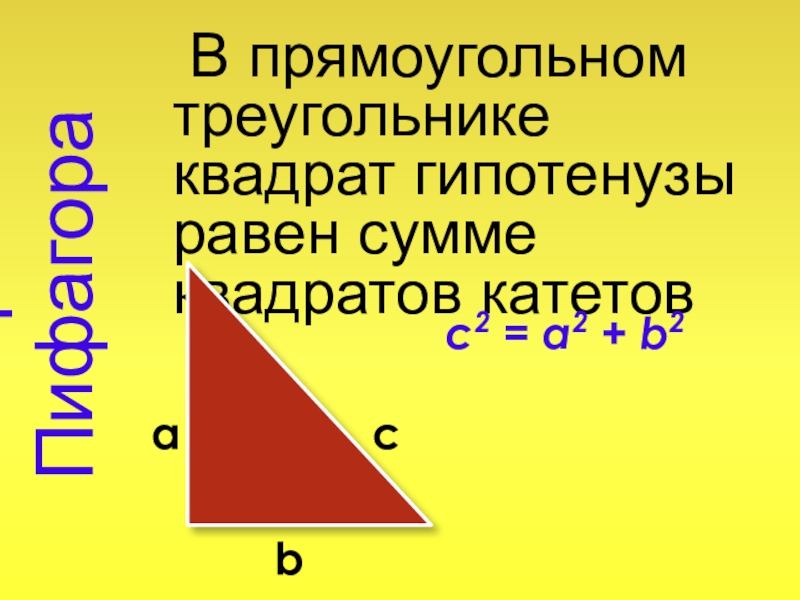
Слайд 7Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов
c2 = a2 + b2
a c
b
Слайд 8Стихотворение о теореме Пифагора
Если дан нам треугольник,
И притом с прямым углом.
То
квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путём
К результату мы придём.
(И. Дырченко)
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путём
К результату мы придём.
(И. Дырченко)
Слайд 14Подведение итогов
Возможно ли было решение задач данного типа без применения теоремы
Пифагора?
В чём суть теоремы Пифагора?
Для любых ли треугольников можно применить данную теорему?
В чём суть теоремы Пифагора?
Для любых ли треугольников можно применить данную теорему?
Слайд 154. В Древнем Египте был известен треугольник со сторонами 3, 4,
5; его использовали при разметке прямоугольных земельных участков после ежегодного уничтожения их границ разлившимся Нилом. Для построения прямых углов египтяне поступали так: на веревке делали метки, делящие ее на 12 равных частей, связывали концы веревки и растягивали на земле с помощью кольев в виде треугольника со сторонами 3, 4 и 5. Тогда угол между сторонами, равными 3 и 4, оказывался прямым.
5. Занимаясь поисками треугольников, стороны которых a, b, c удовлетворяли бы условию a2 + b2 = c2, Пифагор нашел формулы, которые в современной символике могут быть записаны так:
a = 2n + 1, b = 2n(n + 1), c = 2n2 + 2n + 1, n Є Z.
6. Треугольник с такими сторонами является прямоугольным:
n = 1: а = 3, b = 4, с = 5 (приведите примеры самостоятельно).
7. Где применяется, по вашему, сейчас теорема Пифагора?
5. Занимаясь поисками треугольников, стороны которых a, b, c удовлетворяли бы условию a2 + b2 = c2, Пифагор нашел формулы, которые в современной символике могут быть записаны так:
a = 2n + 1, b = 2n(n + 1), c = 2n2 + 2n + 1, n Є Z.
6. Треугольник с такими сторонами является прямоугольным:
n = 1: а = 3, b = 4, с = 5 (приведите примеры самостоятельно).
7. Где применяется, по вашему, сейчас теорема Пифагора?