Презентация, доклад к изучению темы Окружность часть 1

Содержание

1. Презентация к изучению темы Окружность часть 1
2. тема: окружность СОДЕРЖАНИЕ: 1. Длина окружности. Дуга окружности.3. Длина дуги.4. Круг.5. Прямая и окружность.6. Две окружности.
3. Окружностью называется множество точек плоскости, находящихся на
4. Хорда, проходящая через центр окружности, называется диаметром
5. Слайд 5
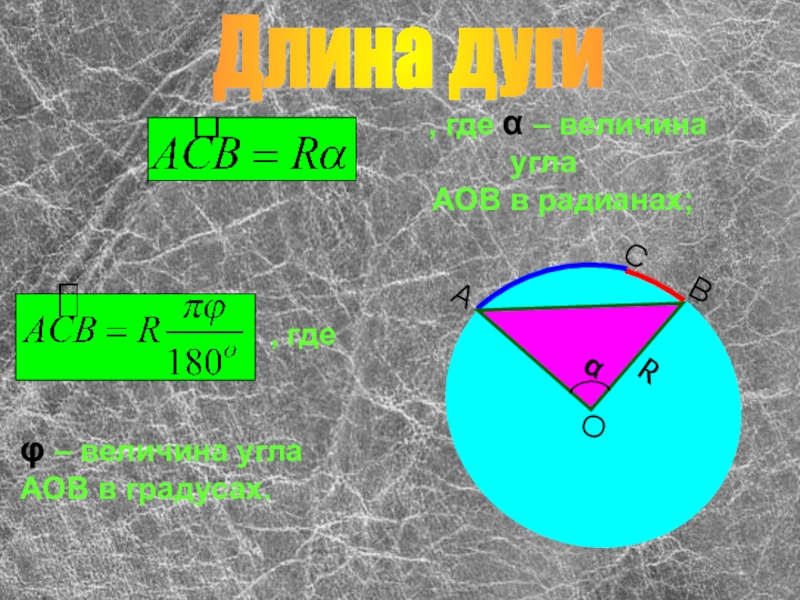
6. Длина дуги , где α
7. Кругом называется часть плоскости,
8. Часть круга, ограниченная дугой и стягивающей ее
9. Часть круга, ограниченная дугой и двумя радиусами,
10. Диаметр, перпендикулярный хорде, делит эту хорду и
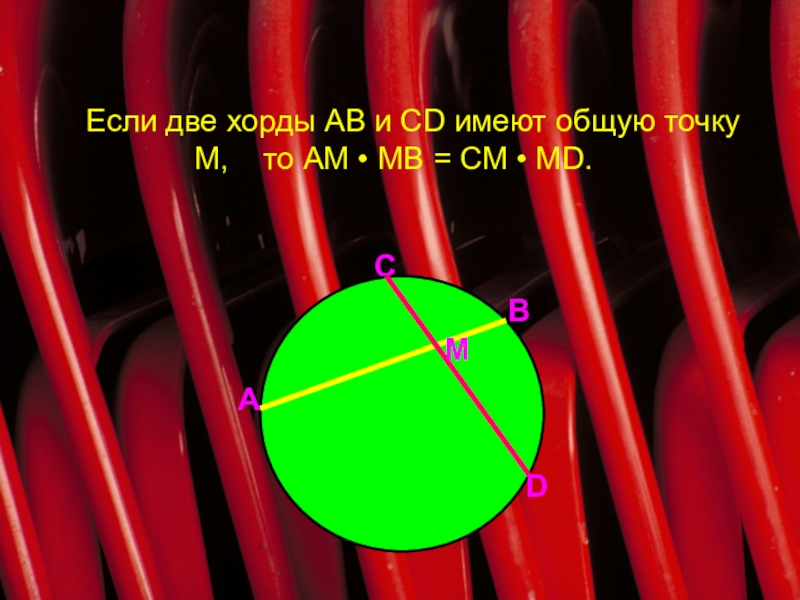
11. Если две хорды АВ и СD имеют
12. Прямая, имеющая с окружностью одну общую точку,
13. Если окружность касается сторон данного угла, то:
14. Если расстояние ОМ от центра окружности до
15. Если расстояние ОМ от центра окружности до
16. Две окружности Если
17. Если R1 + R2 = d или
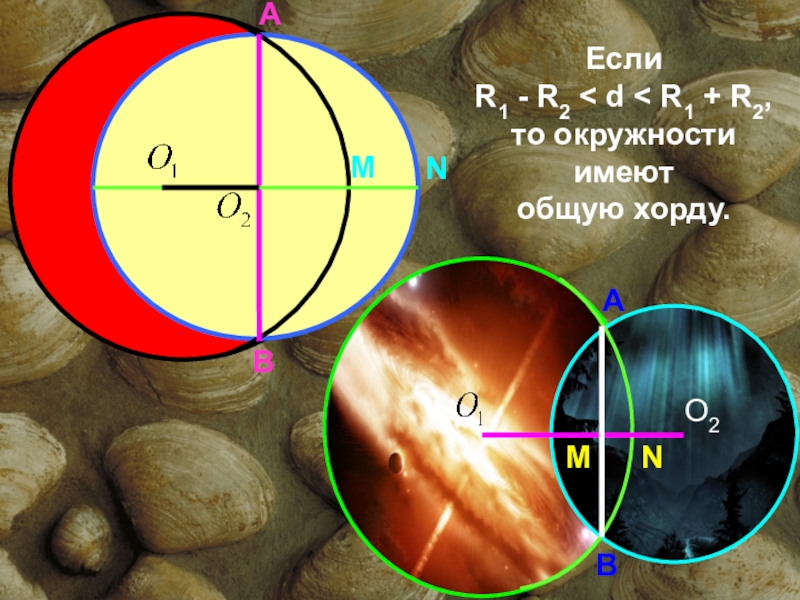
18. Если R1 - R2 < d < R1 + R2, то окружности имеют общую хорду.
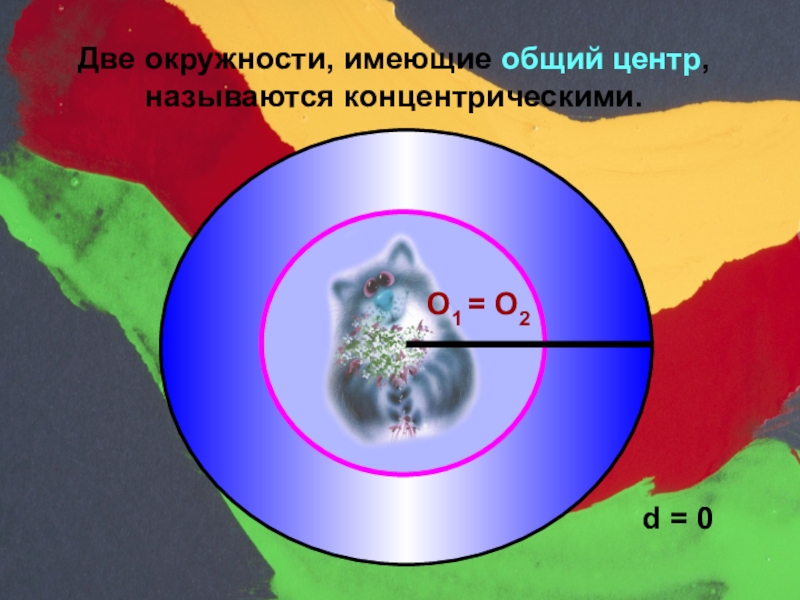
19. Две окружности, имеющие общий центр, называются концентрическими. O1 = O2d = 0

тема: окружность СОДЕРЖАНИЕ: 1. Длина окружности. Дуга окружности.3. Длина дуги.4. Круг.5. Прямая и окружность.6. Две окружности.

Главная
Геометрия
Презентация к изучению темы Окружность часть 1

Слайд 1
Окружность — душа геометрии. Познайте окружность, и вы не только познаете

геометрию, но и возвысите душу свою…

Слайд 2тема:
окружность
СОДЕРЖАНИЕ:
1. Длина окружности.
Дуга окружности.
3. Длина дуги.
4. Круг.
5.

Прямая и окружность.

6. Две окружности.

Слайд 3
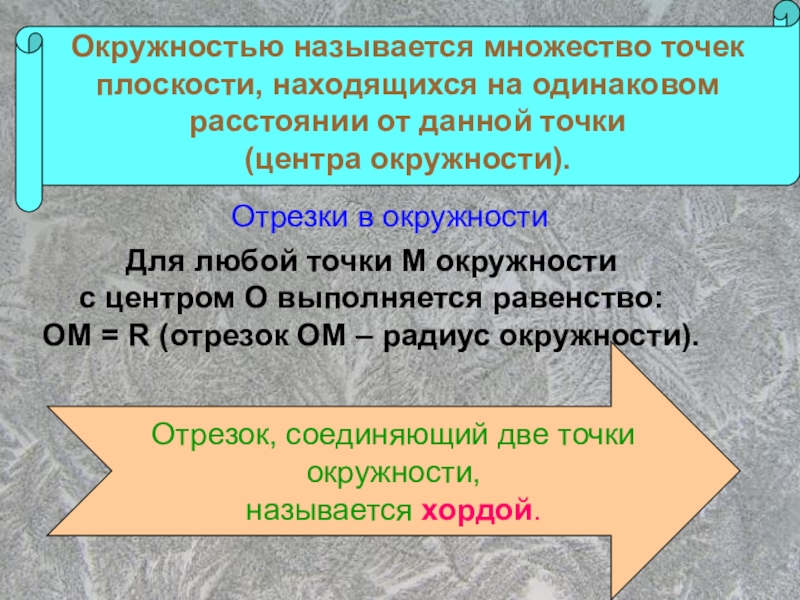
Окружностью называется множество точек плоскости, находящихся на одинаковом расстоянии от данной

точки
(центра окружности).

Отрезки в окружности

Для любой точки М окружности
с центром О выполняется равенство:
ОМ = R (отрезок ОМ – радиус окружности).

Отрезок, соединяющий две точки
окружности,
называется хордой.

Окружностью называется множество точек плоскости, находящихся на одинаковом расстоянии от данной точки (центра окружности).Отрезки в окружностиДля любой

Слайд 4Хорда, проходящая через центр окружности, называется диаметром окружности (D).

Длина окружности

D = 2 R

Хорда, проходящая через центр окружности, называется диаметром окружности (D).

Слайд 5

Дуга окружности

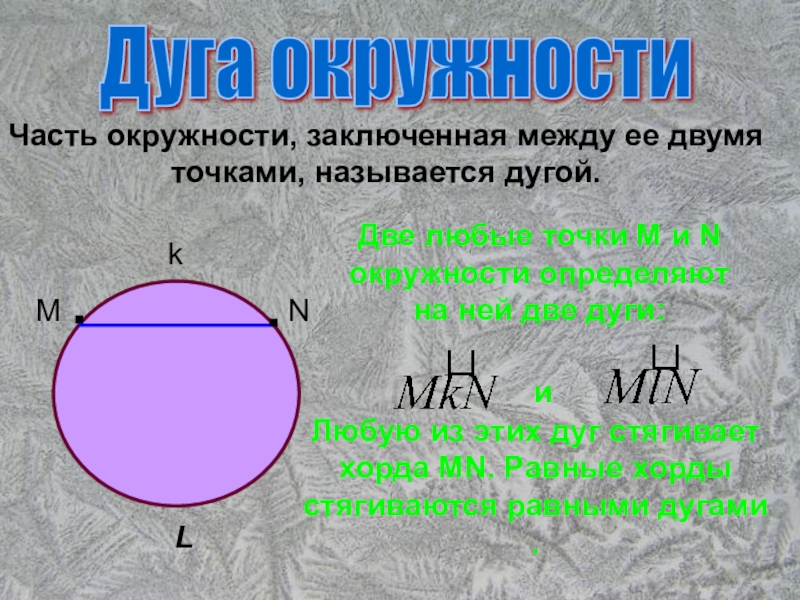
Часть окружности, заключенная между ее двумя
точками, называется дугой.

Две любые точки М и N окружности определяют на ней две дуги:

Любую из этих дуг стягивает хорда MN. Равные хорды стягиваются равными дугами .

Слайд 6 Длина дуги

, где α – величина угла

АОВ в радианах;

, где

φ – величина угла
АОВ в градусах.

Слайд 7
Кругом называется часть плоскости, ограниченная окружностью. Для всех

точек
N круга выполняется неравенство: ОN ≤ R.

Кругом называется часть плоскости, ограниченная окружностью. Для всех точек N круга выполняется неравенство: ОN

Слайд 8Часть круга, ограниченная дугой и стягивающей ее

хордой, называется сегментом.
Любая хорда делит круг на два сегмента. Сегмент, задаваемый диаметром, называется полукругом.

сегмент

Часть круга, ограниченная дугой и стягивающей ее

Слайд 9 Часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с

центром круга, называется сектором круга.
Любые два радиуса
задают два сектора.

сектор

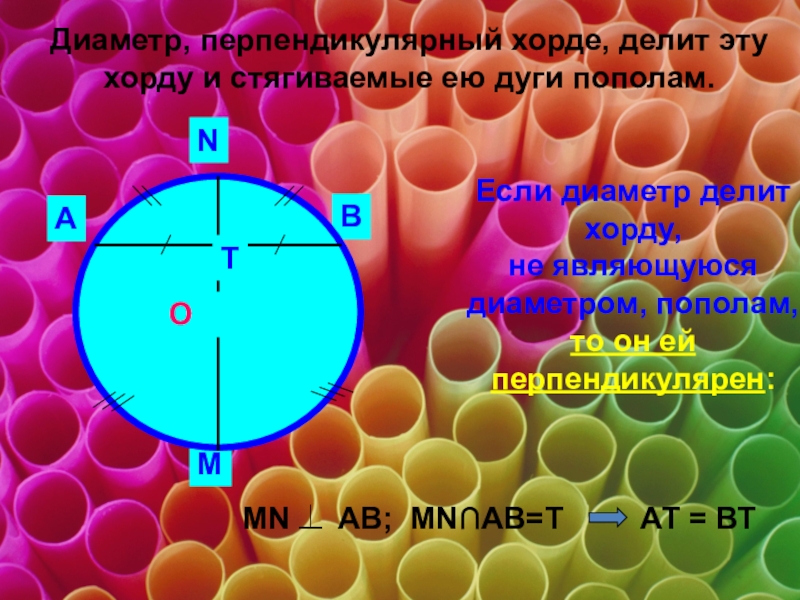
Слайд 10Диаметр, перпендикулярный хорде, делит эту хорду и стягиваемые ею дуги пополам.

Если диаметр делит
хорду,
не являющуюся диаметром, пополам,
то он ей перпендикулярен:

АВ; МN∩AB=T АТ = ВТ

Диаметр, перпендикулярный хорде, делит эту хорду и стягиваемые ею дуги пополам. Если диаметр делит хорду, не являющуюся

Слайд 11Если две хорды АВ и СD имеют общую точку М,

то АМ • МВ = СМ • МD.

Если две хорды АВ и СD имеют общую точку М, то АМ • МВ = СМ

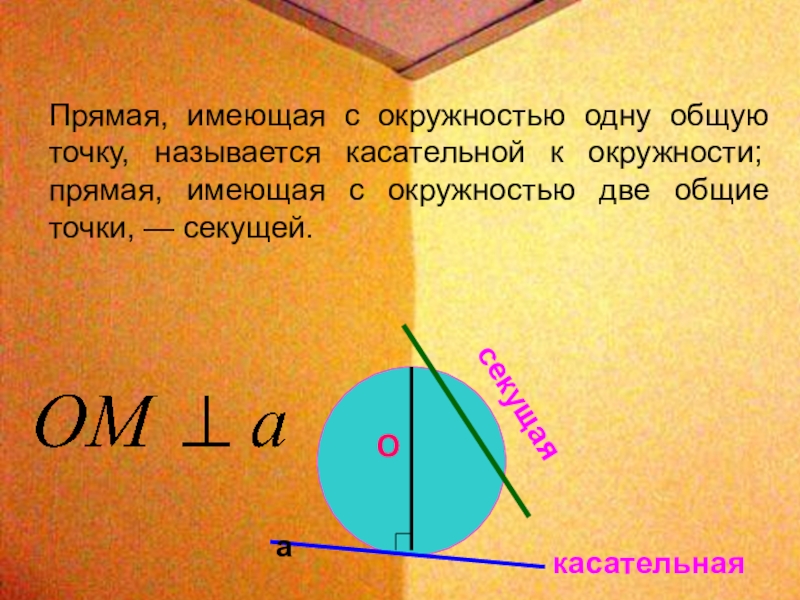
Слайд 12Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности;

прямая, имеющая с окружностью две общие точки, — секущей.

секущая

касательная

Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности; прямая, имеющая с окружностью две общие

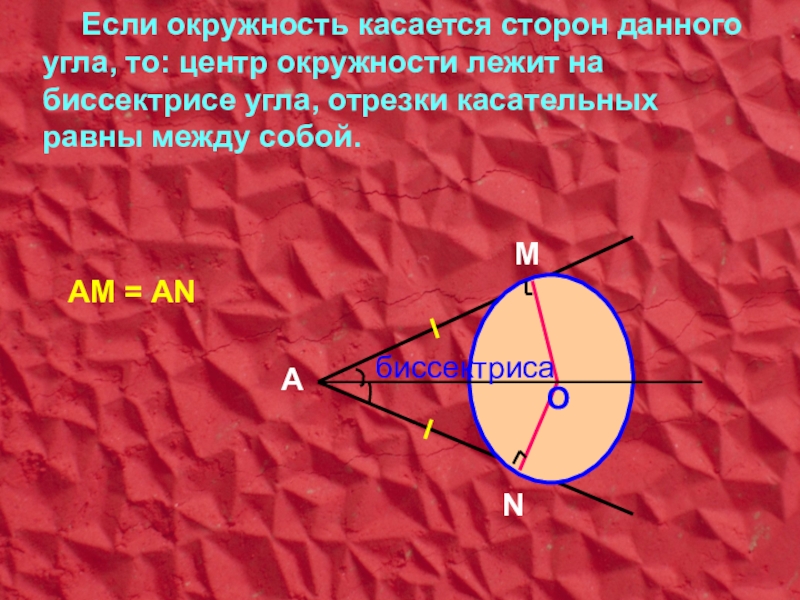
Слайд 13Если окружность касается сторон данного угла, то: центр окружности лежит на

биссектрисе угла, отрезки касательных равны между собой.

АМ = АN

биссектриса

Если окружность касается сторон данного угла, то: центр окружности лежит на биссектрисе угла, отрезки касательных равны между

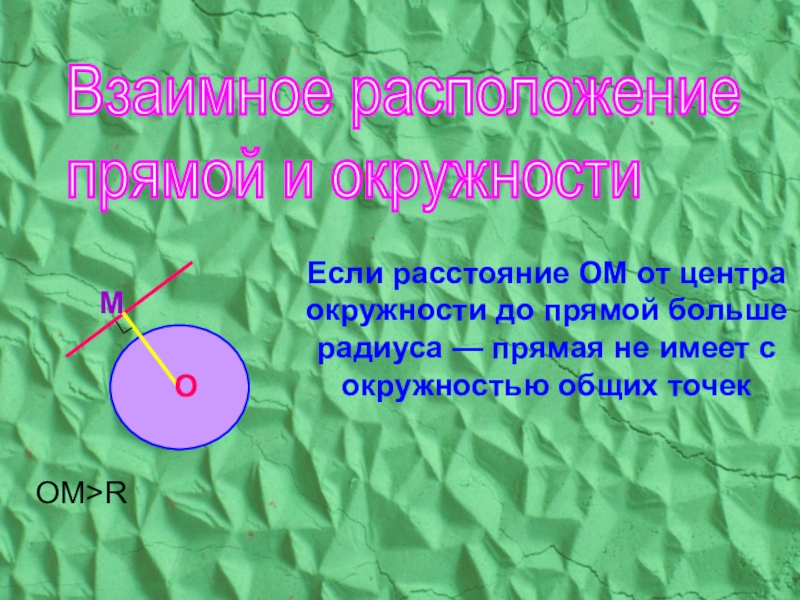
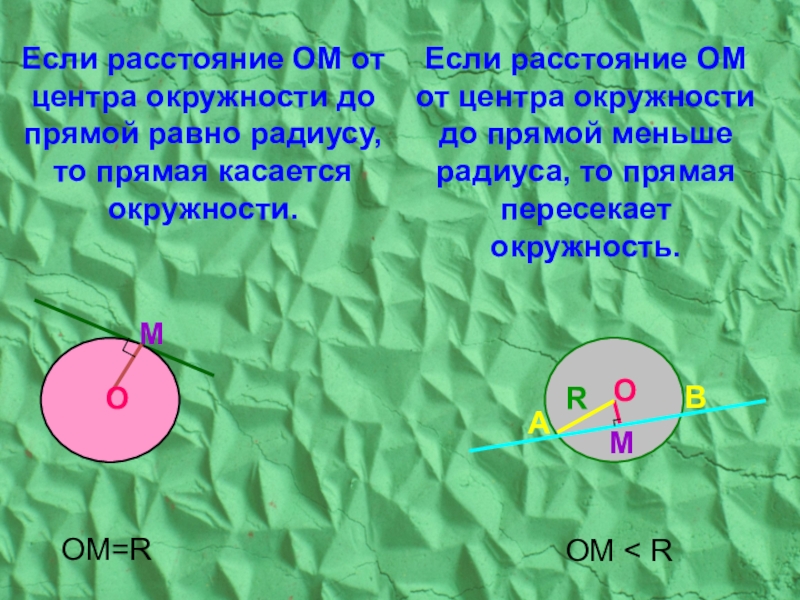
Слайд 14Если расстояние ОМ от центра окружности до прямой больше радиуса —

прямая не имеет с окружностью общих точек

OM>R

Взаимное расположение прямой и окружности

Если расстояние ОМ от центра окружности до прямой больше радиуса — прямая не имеет с окружностью общих

Слайд 15Если расстояние ОМ от центра окружности до прямой равно радиусу, то

прямая касается окружности.

ОМ < R

OM=R

Если расстояние ОМ от центра окружности до прямой меньше радиуса, то прямая пересекает окружность.

Если расстояние ОМ от центра окружности до прямой равно радиусу, то прямая касается окружности. ОМ < R

Слайд 16 Две окружности

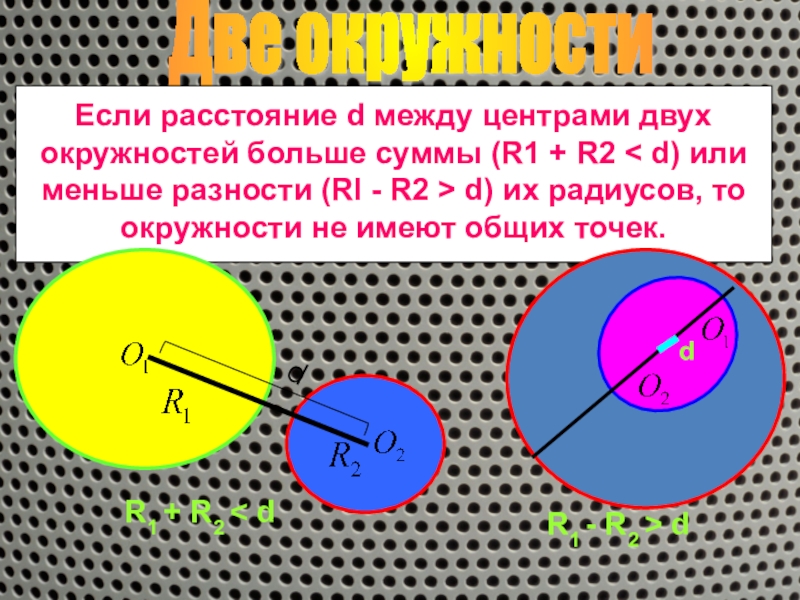
Если расстояние d между центрами

двух окружностей больше суммы (R1 + R2 < d) или меньше разности (Rl - R2 > d) их радиусов, то окружности не имеют общих точек.

R1 + R2 < d

R1 - R2 > d

Две окружности Если расстояние d между центрами двух окружностей больше суммы (R1 +

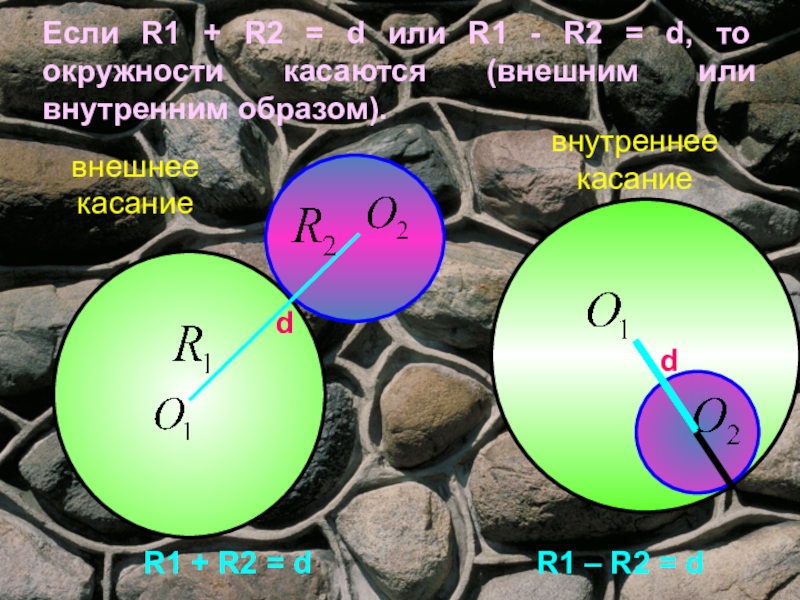
Слайд 17Если R1 + R2 = d или R1 - R2 =

d, то окружности касаются (внешним или внутренним образом).

внутреннее
касание

внешнее
касание

R1 + R2 = d R1 – R2 = d

Если R1 + R2 = d или R1 - R2 = d, то окружности касаются (внешним или

Слайд 18Если
R1 - R2 < d < R1 + R2,
то

окружности
имеют
общую хорду.

Слайд 19Две окружности, имеющие общий центр, называются концентрическими.

O1 = O2
d =

Две окружности, имеющие общий центр, называются концентрическими. O1 = O2d = 0

Скачать презентацию

Презентация, доклад к изучению темы Окружность часть 1

Содержание

Слайд 1
Окружность — душа геометрии. Познайте окружность, и вы не только познаете

Слайд 2тема:
окружность
СОДЕРЖАНИЕ:
1. Длина окружности.
Дуга окружности.
3. Длина дуги.
4. Круг.
5.

Слайд 3
Окружностью называется множество точек плоскости, находящихся на одинаковом расстоянии от данной

Слайд 4Хорда, проходящая через центр окружности, называется диаметром окружности (D).

Слайд 5

Слайд 6 Длина дуги

, где α – величина угла

Слайд 7
Кругом называется часть плоскости, ограниченная окружностью. Для всех

Слайд 8Часть круга, ограниченная дугой и стягивающей ее

Слайд 9 Часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с

Слайд 10Диаметр, перпендикулярный хорде, делит эту хорду и стягиваемые ею дуги пополам.

Слайд 11Если две хорды АВ и СD имеют общую точку М,

Слайд 12Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности;

Слайд 13Если окружность касается сторон данного угла, то: центр окружности лежит на

Слайд 14Если расстояние ОМ от центра окружности до прямой больше радиуса —

Слайд 15Если расстояние ОМ от центра окружности до прямой равно радиусу, то

Слайд 16 Две окружности

Если расстояние d между центрами

Слайд 17Если R1 + R2 = d или R1 - R2 =

Слайд 18Если
R1 - R2 < d < R1 + R2,
то

Слайд 19Две окружности, имеющие общий центр, называются концентрическими.

O1 = O2
d =

Что такое shareslide.ru?

Обратная связь

Презентация, доклад к изучению темы Окружность часть 1

Содержание

Слайд 1 Окружность — душа геометрии. Познайте окружность, и вы не только познаете

Слайд 2тема: окружность СОДЕРЖАНИЕ: 1. Длина окружности. Дуга окружности.3. Длина дуги.4. Круг.5.

Слайд 3Окружностью называется множество точек плоскости, находящихся на одинаковом расстоянии от данной

Слайд 4Хорда, проходящая через центр окружности, называется диаметром окружности (D).

Слайд 5

Слайд 6 Длина дуги , где α – величина угла

Слайд 7 Кругом называется часть плоскости, ограниченная окружностью. Для всех

Слайд 8Часть круга, ограниченная дугой и стягивающей ее

Слайд 9 Часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с

Слайд 10Диаметр, перпендикулярный хорде, делит эту хорду и стягиваемые ею дуги пополам.

Слайд 11Если две хорды АВ и СD имеют общую точку М,

Слайд 12Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности;

Слайд 13Если окружность касается сторон данного угла, то: центр окружности лежит на

Слайд 14Если расстояние ОМ от центра окружности до прямой больше радиуса —

Слайд 15Если расстояние ОМ от центра окружности до прямой равно радиусу, то

Слайд 16 Две окружности Если расстояние d между центрами

Слайд 17Если R1 + R2 = d или R1 - R2 =

Слайд 18Если R1 - R2 < d < R1 + R2, то

Слайд 19Две окружности, имеющие общий центр, называются концентрическими. O1 = O2d =

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 1
Окружность — душа геометрии. Познайте окружность, и вы не только познаете

Слайд 2тема:
окружность
СОДЕРЖАНИЕ:
1. Длина окружности.
Дуга окружности.
3. Длина дуги.
4. Круг.
5.

Слайд 3
Окружностью называется множество точек плоскости, находящихся на одинаковом расстоянии от данной

Слайд 6 Длина дуги

, где α – величина угла

Слайд 7
Кругом называется часть плоскости, ограниченная окружностью. Для всех

Слайд 16 Две окружности

Если расстояние d между центрами

Слайд 18Если
R1 - R2 < d < R1 + R2,
то

Слайд 19Две окружности, имеющие общий центр, называются концентрическими.

O1 = O2
d =