Выполнила:
ученица 7 «Б» класса
МБОУ «Гимназия № 2»
Иваницкая Алина
Руководитель работы:
Новикова Т.Н.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад исследовательской работы Сравнение треугольников в геометрии Евклида и геометрии Лобачевского
Содержание
- 1. Презентация исследовательской работы Сравнение треугольников в геометрии Евклида и геометрии Лобачевского
- 2. Слайд 2
- 3. Этапы работы1. Изучение теоретической основы понятия «Треугольник»
- 4. Слайд 4
- 5. Геометрия возникла очень давно, это одна из
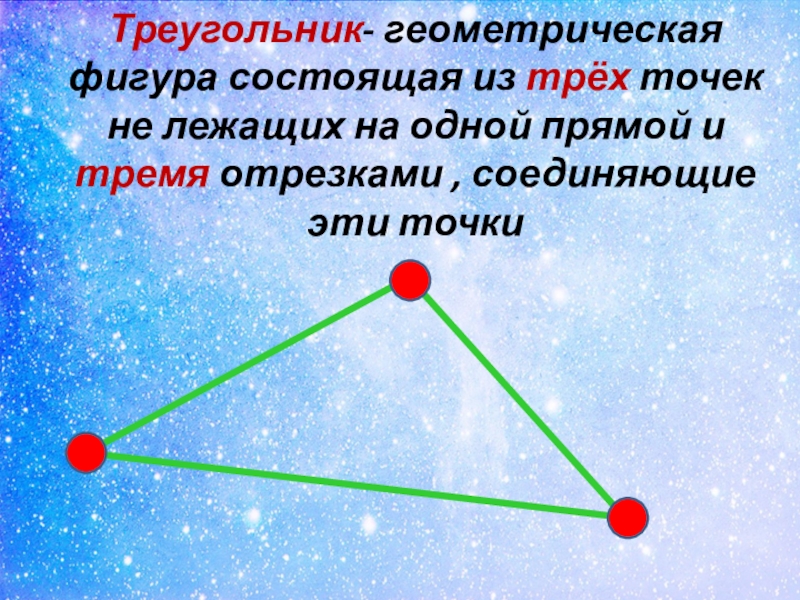
- 6. Треугольник- геометрическая фигура состоящая из трёх точек
- 7. Традиционно считается, что родоначальниками геометрии являются древние
- 8. «Египетский треугольник» Название «египетский треугольник» появилось уже в
- 9. Треугольник-мистическая фигура .Он окутан множеством историй
- 10. Также на уроках географии мы ,
- 11. Треугольники в природеКогда мы обсуждали работу, то
- 12. Благодаря этой информации, мы показали ,
- 13. Выдающийся математик Евклид
- 14. Слайд 14
- 15. Николай Иванович Лобачевский-русский математик, создатель неевклидовой геометрии
- 16. Развитию и распространению идей Лобачевского содействовали своими трудами такие замечательные учёные:
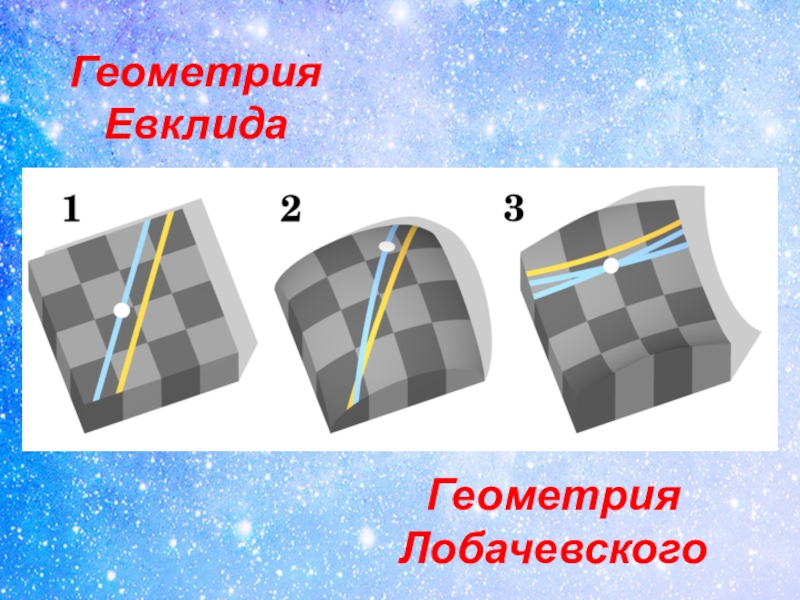
- 17. Геометрия ЕвклидаГеометрия Лобачевского
- 18. «Чем отличается геометрия Лобачевского от геометрии
- 19. Вывод: геометрия Лобачевского отличается от евклидовой
- 20. Подобные треугольникиГеометрия ЕвклидаВ геометрии Евклида существуют
- 21. Различие в признаках равенства треугольниковГеометрия ЕвклидаВ Геометрии
- 22. Сумма углов треугольникаГеометрия Евклида Как, например, в
- 23. Сумма углов треугольникаГеометрия ЛобачевскогоТак как в геометрии
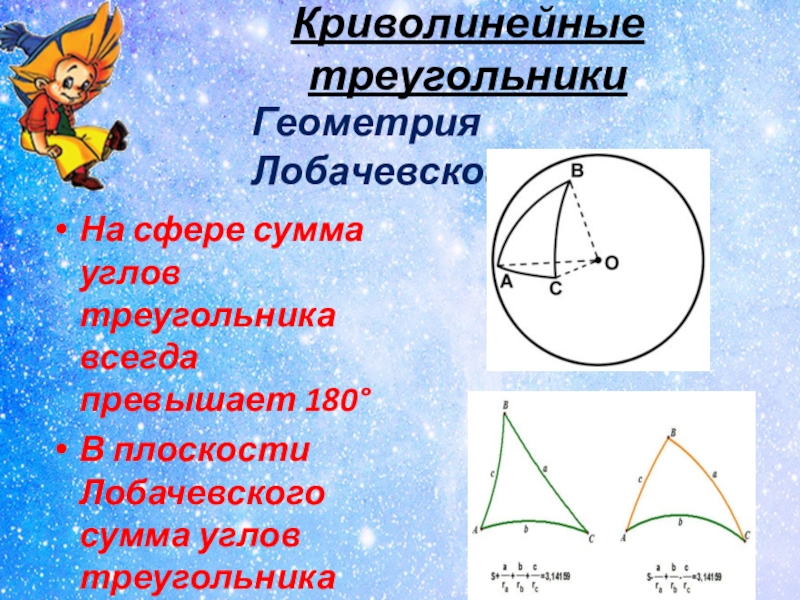
- 24. Криволинейные треугольникиНа сфере сумма углов треугольника всегда
- 25. Геометрия Евклида и геометрия Лобачевского 1)Геометрия на
- 26. Заседания
- 27. 1.Геометрия Евклида работает на маленькой
- 28. Спасибо за внимание!!!
Слайд 1
Слайд 2 Цель работы : проанализировать
Слайд 3Этапы работы
1. Изучение теоретической основы понятия «Треугольник»
2.Изучение особенностей геометрии Евклида и Лобачевского.
3.Сопоставление понятия «Треугольник» в геометрии Евклида и геометрии Лобачевского.
4.Изготовление наглядного электронного пособия по материалам исследовательской работы .
5.Практическое применение практических знаний на занятиях факультатива.
6.Оформление работы ,презентации на конференцию.
Слайд 4 Задачи работы 1.История треугольника 2.Увидеть треугольники
Слайд 5Геометрия возникла очень давно, это одна из самых древних наук. Геометрия
.
Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений
Слайд 6Треугольник- геометрическая фигура состоящая из трёх точек не лежащих на одной
Слайд 7Традиционно считается, что родоначальниками геометрии являются древние греки, перенявшие у египтян
Немного из истории…
Слайд 8«Египетский треугольник»
Название «египетский треугольник» появилось уже в 5 веке до н.э.
Принадлежит оно прямоугольному треугольнику, стороны которого равны соответственно 3, 4 и 5. Назван он был так потому, что очень широко применялся еще в Древнем Египте в различных сферах жизнедеятельности. Хотя уже тогда он был знаком людям далеко за пределами Древнего Египта, но, видимо, его уникальные свойства заметили и начали использовать впервые именно там.
Слайд 9 Треугольник-мистическая фигура .Он окутан множеством историй ,легенд и тайн. Берму́дский треуго́льник
Слайд 10 Также на уроках географии мы , узнавая всё больше и больше
Слайд 11Треугольники в природе
Когда мы обсуждали работу, то глядя в окно мы
Слайд 12 Благодаря этой информации, мы показали , что треугольники можно встретить не
Слайд 14 Основные постулаты Евклида: Из каждой
Слайд 15Николай Иванович Лобачевский-русский математик, создатель неевклидовой геометрии ,деятель университетского образования и
Слайд 16Развитию и распространению идей Лобачевского содействовали своими трудами такие замечательные учёные:
Слайд 18
«Чем отличается геометрия Лобачевского
от геометрии Евклида?»
Евклидова геометрия
Евклидова аксиома о параллельных прямых:
Геометрия Лобачевского
Аксиома Лобачевского о параллельных прямых: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
Слайд 19 Вывод: геометрия Лобачевского отличается от евклидовой лишь в одной аксиоме —
Слайд 20Подобные треугольники
Геометрия Евклида
В геометрии Евклида существуют
Геометрия Лобачевского
В геометрии Лобачевского не существует подобных треугольников
Слайд 21Различие в признаках равенства треугольников
Геометрия Евклида
В Геометрии Евклида существует всего 3
Геометрия Лобачевского
В геометрии Лобачевского имеет место четвертый признак равенства треугольников: если углы одного треугольника соответственно равны углам другого треугольника, то эти треугольники равны.
Слайд 22Сумма углов треугольника
Геометрия Евклида
Как, например, в геометрии Евклида доказывается, что
Слайд 23Сумма углов треугольника
Геометрия Лобачевского
Так как в геометрии Лобачевского параллельность сохраняется только
Слайд 24Криволинейные треугольники
На сфере сумма углов треугольника всегда превышает 180°
В плоскости Лобачевского
Геометрия Лобачевского
Слайд 25Геометрия Евклида и геометрия Лобачевского
1)Геометрия на плоскости
2)Существуют признаки подобных треугольников
3) 3 признака равенства треугольников
4)Сумма углов треугольника всегда равна 180°
1)Геометрия в пространстве
2)Подобных треугольников не существует
3)4 признака равенства треугольников
4)Сумма углов треугольника меньше 180°, а на сфере больше180°
Слайд 27 1.Геометрия Евклида работает на маленькой поверхности, а геометрия Лобачевского на развернутой
Вывод работы