учащаяся 9 «Б» класса
МБОУ г. Костромы «СОШ № 27»
Научный руководитель: Краснова Елена
Вячеславовна,
учитель математики
МБОУ г. Костромы «СОШ №27»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Исследование свойств икосаэдра
Содержание
- 1. Презентация Исследование свойств икосаэдра
- 2. АктуальностьИзучение сложной пространственной фигуры – икосаэдра –
- 3. ЦельИсследовать свойства икосаэдра как одного из представителей правильных многогранников.
- 4. ЗадачиВыяснить, почему правильные многогранники (в том числе
- 5. Объект и предмет исследования: Икосаэдр
- 6. Формулирование проблемыПравильные многогранники имеют совершенную форму. Икосаэдр – самый интересный, на мой взгляд, представитель правильных многогранников.
- 7. ПроблемаСвойства икосаэдра являются следствием его своеобразной формы.
- 8. Высказывания известных людей о икосаэдре. «Правильных многогранников
- 9. ОпределениеИкосаэдр(от греческого eikosi – двадцать и hedra
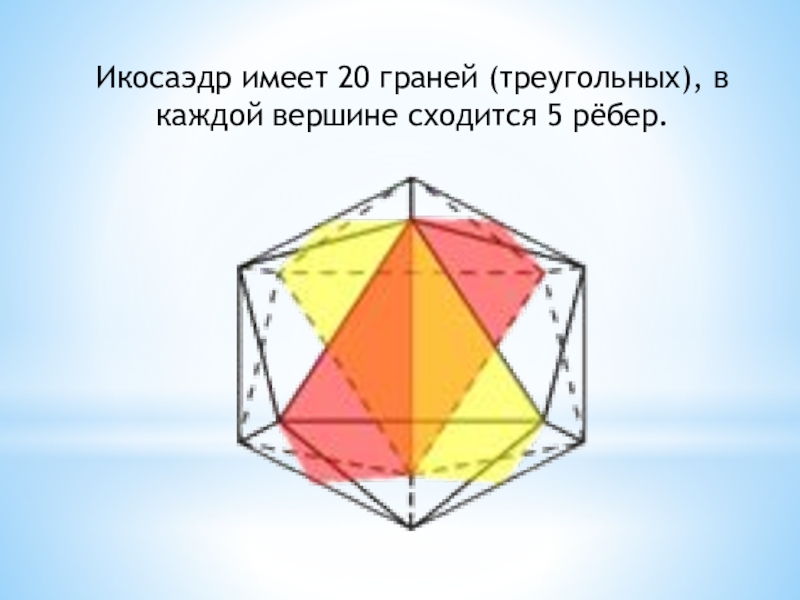
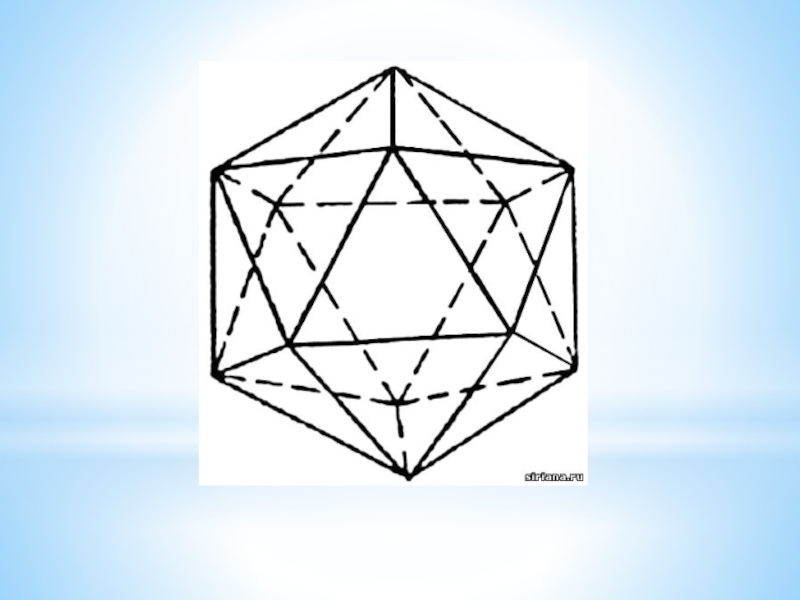
- 10. Икосаэдр имеет 20 граней (треугольных), в каждой вершине сходится 5 рёбер.
- 11. Свойства икосаэдраИкосаэдр –тело, ограниченное двадцатью многоугольниками; правильный
- 12. Слайд 12
- 13. Радиусы, площади и объемыПлощадь икосаэдра: Объем икосаэдра:
- 14. Леонард Эйлер(1707 – 1783) — швейцарский, немецкий
- 15. Изготовление модели икосаэдра.1 способ. Если поверхность многогранника
- 16. Изготовление модели икосаэдра.2 способ. Есть ещё один
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. В сферу орбиты Сатурна он вписывает куб,
- 21. Спасибо за внимание!
АктуальностьИзучение сложной пространственной фигуры – икосаэдра – позволяет повысить мотивацию учащихся, помогает преодолеть трудности в пространственном восприятии фигуры.
Слайд 2Актуальность
Изучение сложной пространственной фигуры – икосаэдра – позволяет повысить мотивацию учащихся,
помогает преодолеть трудности в пространственном восприятии фигуры.
Слайд 4Задачи
Выяснить, почему правильные многогранники (в том числе икосаэдр) получили именно такое
название.
Изучить особенности икосаэдра.
Изготовить модель икосаэдра.
Узнать, где можно встретить эти удивительные тела.
Изучить особенности икосаэдра.
Изготовить модель икосаэдра.
Узнать, где можно встретить эти удивительные тела.
Слайд 6Формулирование проблемы
Правильные многогранники имеют совершенную форму. Икосаэдр – самый интересный, на
мой взгляд, представитель правильных многогранников.
Слайд 8Высказывания известных людей о икосаэдре.
«Правильных многогранников вызывающе мало, но этот весьма
скромный по численности отряд сумел пробраться в самые глубины различных наук».
Л. Кэрролл.
Л. Кэрролл.
Слайд 9Определение
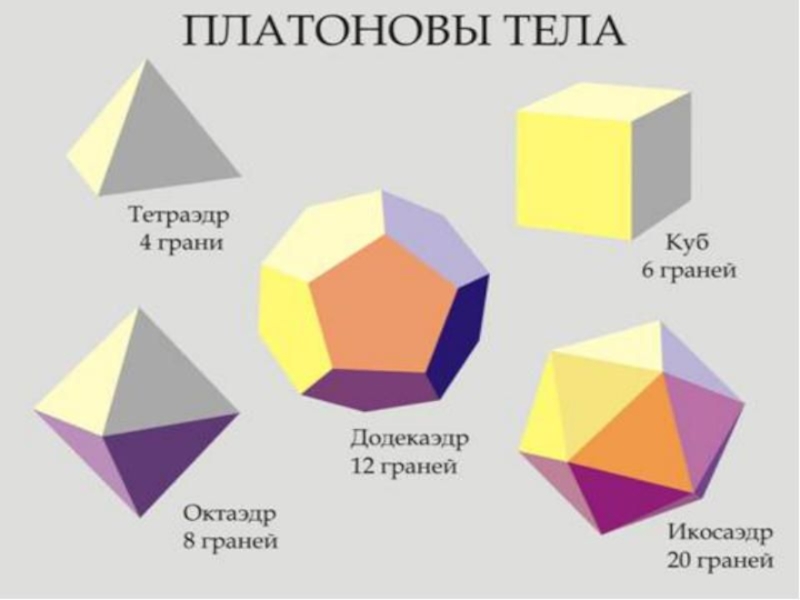
Икосаэдр(от греческого eikosi – двадцать и hedra – грань) — правильный
выпуклый многогранник, двадцатигранник, один из тел Платона.
Слайд 11Свойства икосаэдра
Икосаэдр –тело, ограниченное двадцатью многоугольниками; правильный икосаэдр ограничен двадцатью равносторонними
треугольниками. Икосаэдр состоит из 59 звёздчатых форм. Все 12 вершин икосаэдра являются вершинами 5 равносторонних треугольников, значит, сумма углов у вершины равна 300°.
Слайд 13Радиусы, площади и объемы
Площадь икосаэдра:
Объем икосаэдра:
Радиус вписанной в икосаэдр
сферы:
Радиус описанной вокруг икосаэдра сферы:
Радиус описанной вокруг икосаэдра сферы:
Слайд 14Леонард Эйлер(1707 – 1783) — швейцарский, немецкий и российский математик и
механик, внёсший фундаментальный вклад в развитие этих наук.
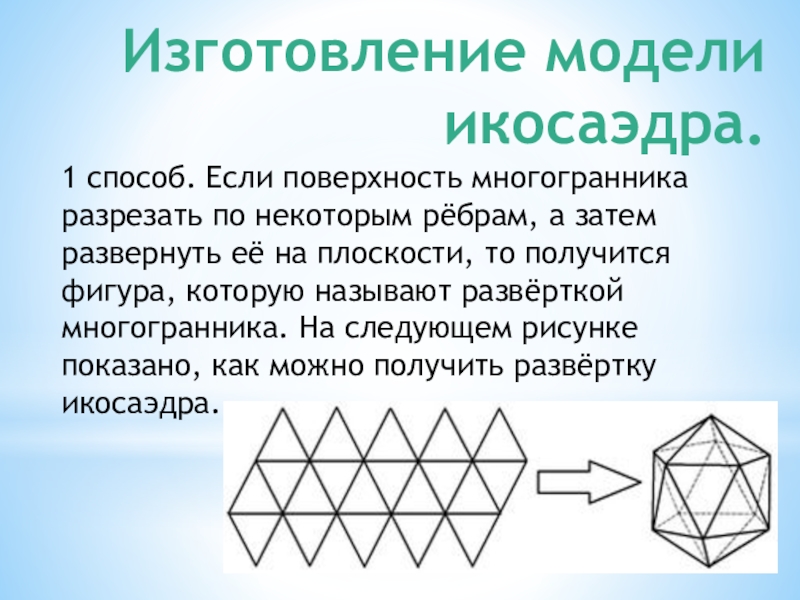
Слайд 15Изготовление модели икосаэдра.
1 способ. Если поверхность многогранника разрезать по некоторым рёбрам,
а затем развернуть её на плоскости, то получится фигура, которую называют развёрткой многогранника. На следующем рисунке показано, как можно получить развёртку икосаэдра.
Слайд 16Изготовление модели икосаэдра.
2 способ. Есть ещё один способ изготовления многогранников, при
котором они сплетаются из нескольких полосок бумаги. Без применения клея модель приобретает жёсткую структуру после того, как будет заправлен последний кусочек бумаги.
Слайд 20В сферу орбиты Сатурна он вписывает куб, в куб - сферу
Юпитера, в сферу Юпитера - тетраэдр, и так далее последовательно вписываются друг в друга сфера Марса - додекаэдр, сфера Земли - икосаэдр, сфера Венеры - октаэдр, сфера Меркурия.