- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад II признак равенства треугольников
Содержание
- 1. Презентация: II признак равенства треугольников
- 2. Какие треугольники называются равными?
- 3. Устно: Вставьте в предложения подходящие слова так,
- 4. Задание 1: Заполнить пропуски так, чтобы получились предложения, соответствующие данному чертежу.1.Градусная мера углов
- 5. Задание 2:Построить треугольник по стороне АС=6 см и прилежащим к ней углам:
- 6. II признак равенства треугольников(Угол-Сторона-Угол, УСУ)Теорема: Если сторона
- 7. Задание 3:Построить треугольник с помощью линейки и транспортира по следующим значениям двух углов и стороне:
- 8. 23см540Для красного трекугольника найдите равный ему и щелкните по нему мышкой.23см23см54023см540840840840Проверка540Неправильно!SKDАNIOCBMEZ
- 9. В Милете, в одной из гаваней, Фалес
- 10. Домашнее задание: п.19,вопрос 14 стр.50, №122, №124
Какие треугольники называются равными? Как можно узнать, равны ли данные треугольники? Какие элементы достаточно рассмотреть для доказательства равенства треугольников?
Слайд 2 Какие треугольники называются равными?
Как можно узнать,
равны ли данные треугольники?
Какие элементы достаточно рассмотреть для доказательства равенства треугольников?
Какие элементы достаточно рассмотреть для доказательства равенства треугольников?
Слайд 3Устно:
Вставьте в предложения подходящие слова так, чтобы получились верные утверждения.
1.
Периметр равностороннего треугольника в
три раза больше
длины его стороны
2. Если AK и BN – медианы треугольника ABC, то третья медиана этого треугольника пройдёт
через точку пересечения медиан AK и BN.
3. Если две стороны и угол между ними одного
треугольника соответственно равны двум сторонам
и углу между ними
другого треугольника
то такие треугольники.
три раза больше
длины его стороны
2. Если AK и BN – медианы треугольника ABC, то третья медиана этого треугольника пройдёт
через точку пересечения медиан AK и BN.
3. Если две стороны и угол между ними одного
треугольника соответственно равны двум сторонам
и углу между ними
другого треугольника
то такие треугольники.
Слайд 4Задание 1:
Заполнить пропуски так, чтобы получились предложения, соответствующие
данному чертежу.
1.Градусная мера углов
равна сорока пяти градусам.
2. На чертеже изображено три равных отрезка
HB,AH, CH,
длина каждого из которых равна 3,5см .
3. Изображенные на чертеже треугольники :
∆АНС, ∆ САВ
равнобедренные. Они имеют по два
равных
угла с градусной мерой
45 градусов .
1.Градусная мера углов
2. На чертеже изображено три равных отрезка
HB,AH, CH,
длина каждого из которых равна 3,5см .
3. Изображенные на чертеже треугольники :
∆АНС, ∆ САВ
равнобедренные. Они имеют по два
равных
угла с градусной мерой
45 градусов .
Слайд 6II признак равенства треугольников
(Угол-Сторона-Угол, УСУ)
Теорема: Если сторона и два прилежащих к
ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Дано: ∆ A1B1C1, ∆A2B2C2
< A1= <С1= <С2,
A1C1=A2C2
Д-ть: ∆ A1B1C1 = ∆ A2B2C2
Д-во:
Наложим ∆A1B1C1 на ∆A2B2C2 так, чтобы совпали равные стороны A1C1 и A2C2.
Т. к. < A1=а т.к. <С1= <С2,то сторона C1B1 пойдет по стороне C2 B2.
т.B1 пересечения сторон A1B1 и C1B1 совпадет с т.B2 пересечения сторон A2B2 и C2 B2.
Итак, все вершины ∆A1B1C1 совпали с соответствующими вершинами ∆A2B2C2.
=> ∆ A1B1C1 = ∆ A2B2C2
Ч.Т.Д.
Дано: ∆ A1B1C1, ∆A2B2C2
< A1=
A1C1=A2C2
Д-ть: ∆ A1B1C1 = ∆ A2B2C2
Д-во:
Наложим ∆A1B1C1 на ∆A2B2C2 так, чтобы совпали равные стороны A1C1 и A2C2.
Т. к. < A1=
т.B1 пересечения сторон A1B1 и C1B1 совпадет с т.B2 пересечения сторон A2B2 и C2 B2.
Итак, все вершины ∆A1B1C1 совпали с соответствующими вершинами ∆A2B2C2.
=> ∆ A1B1C1 = ∆ A2B2C2
Ч.Т.Д.
Слайд 7Задание 3:
Построить треугольник с помощью линейки и транспортира по следующим значениям
двух углов и стороне:
Слайд 8
23см
540
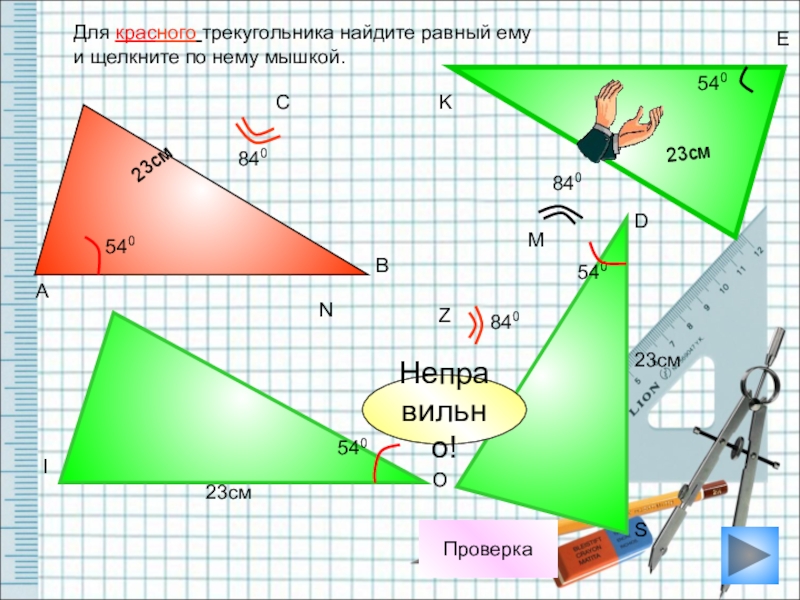
Для красного трекугольника найдите равный ему
и щелкните по нему мышкой.
23см
23см
540
23см
540
840
840
840
Проверка
540
Неправильно!
S
K
D
А
N
I
O
C
B
M
E
Z
Слайд 9В Милете, в одной из гаваней, Фалес установил дальномер – прибор,
который позволял определять расстояние от берега до корабля, находящегося далеко в море
А
В
С
D
Е