- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Гл. 1. Урок 4. Признаки параллелограмма.
Содержание
- 1. Презентация. Гл. 1. Урок 4. Признаки параллелограмма.
- 2. Задачи урока:
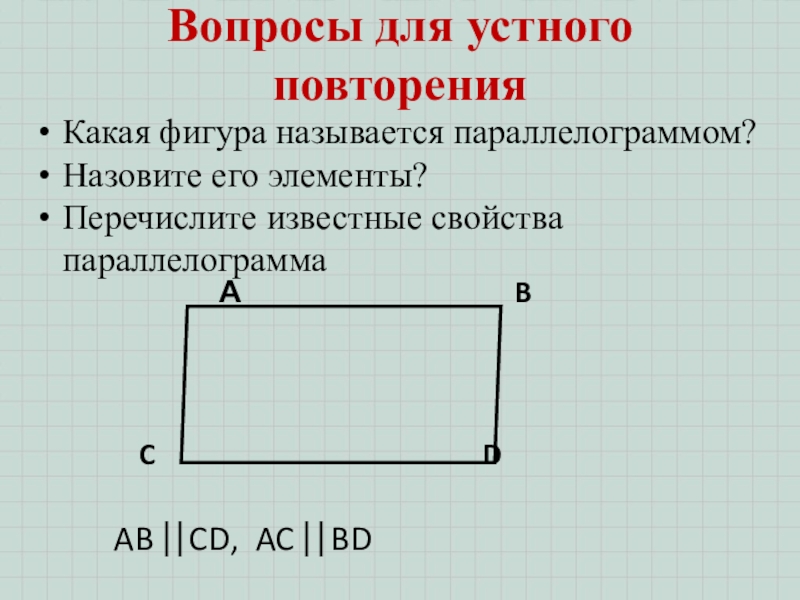
- 3. АBCDAB ⎢⎢CD, AC ⎢⎢BD Вопросы для устного повторенияКакая фигура называется параллелограммом?Назовите его элементы?Перечислите известные свойства параллелограмма
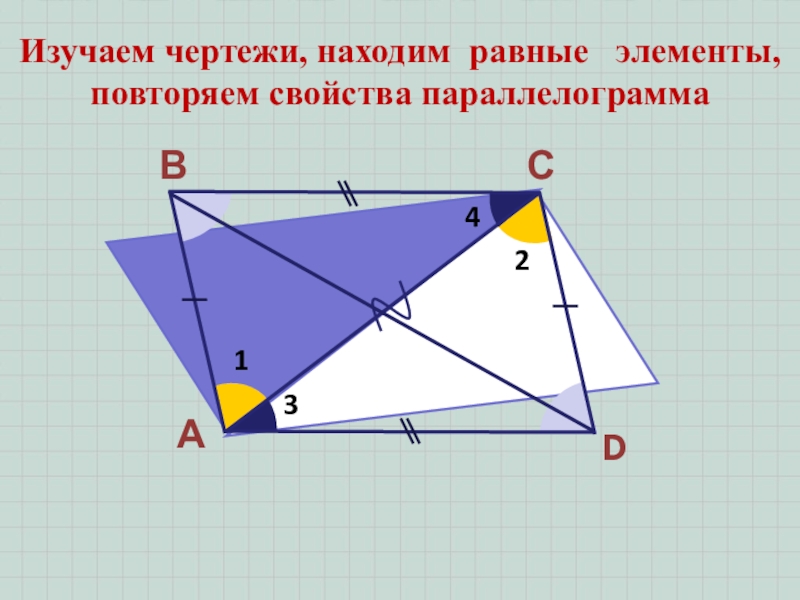
- 4. АВСD1234Изучаем чертежи, находим равные элементы, повторяем свойства параллелограмма
- 5. Если …, то …Условие теоремыЗаключение теоремы
- 6. Теоремой, обратной данной,
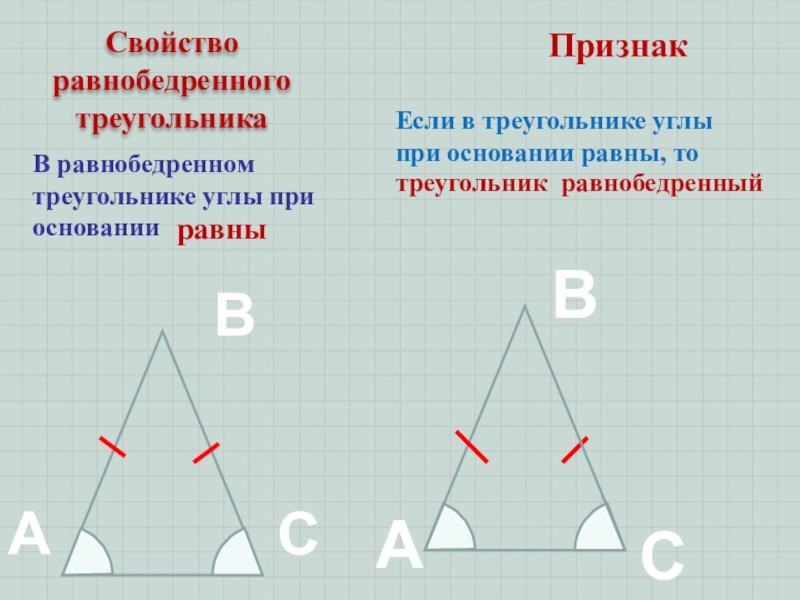
- 7. Свойство равнобедренного треугольникаВСВ равнобедренном треугольнике углы при
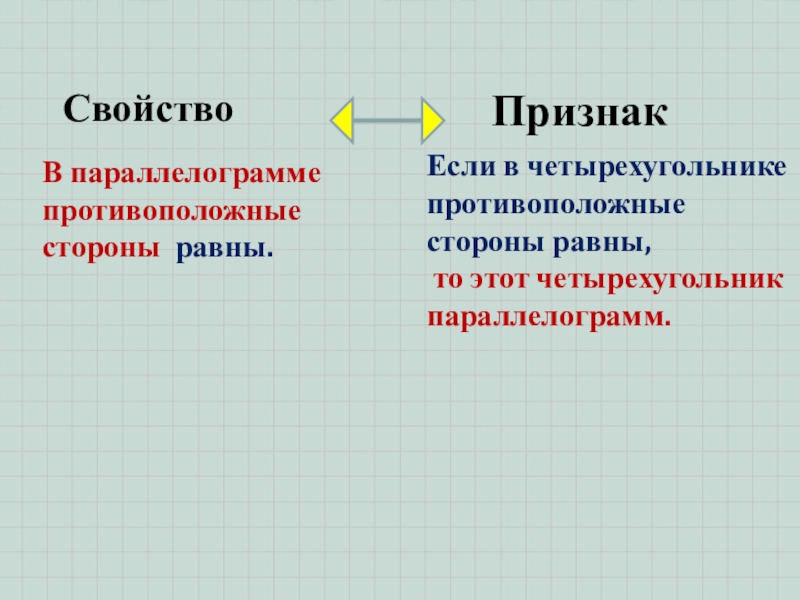
- 8. В параллелограмме противоположные стороны равны.Если в четырехугольнике противоположные стороны равны, то этот четырехугольник параллелограмм.СвойствоПризнак
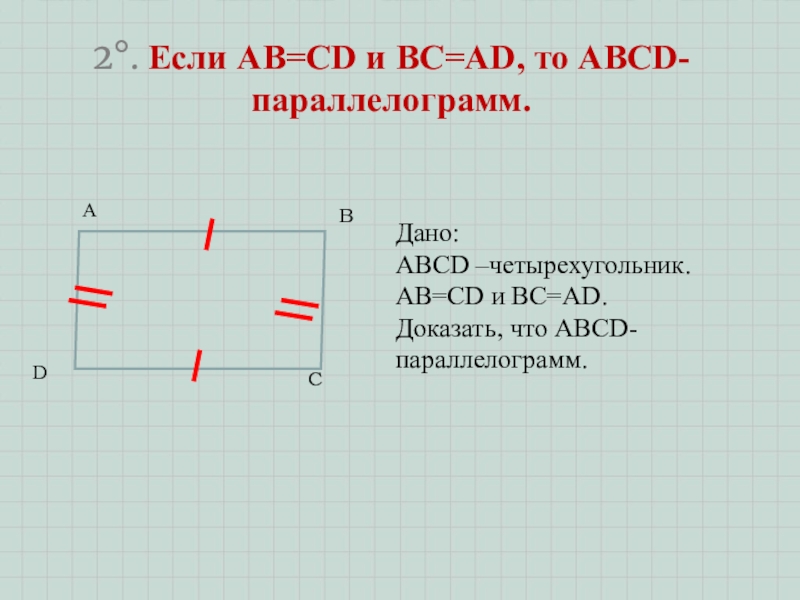
- 9. 2°. Если AB=CD и BC=AD, то ABCD-параллелограмм. АBCДано:ABCD –четырехугольник. AB=CD и BC=AD.Доказать, что ABCD-параллелограмм.D
- 10. В параллелограмме диагонали точкой пересечения делятся пополам.Если
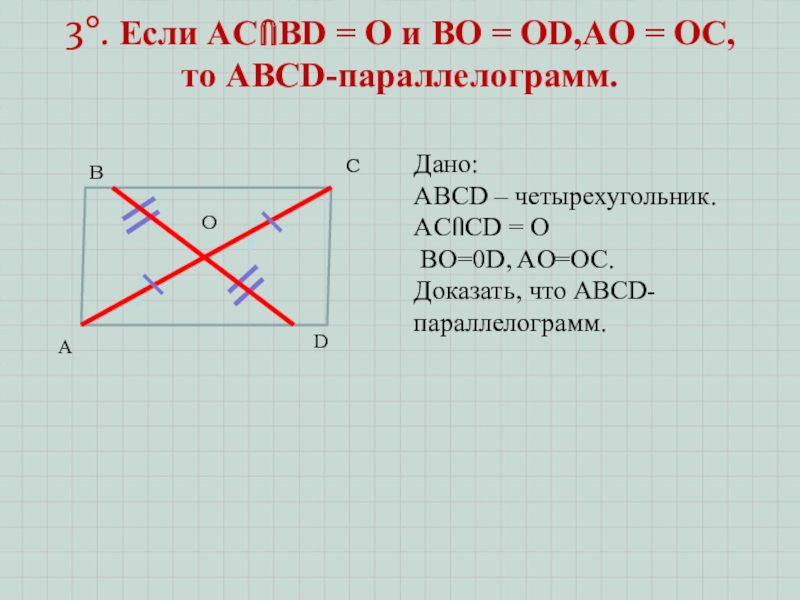
- 11. 3°. Если ACՈBD = O и BO
- 12. Если AB=CD и AB||CD, то ABCD-параллелограмм. АBCDДано:ABCD
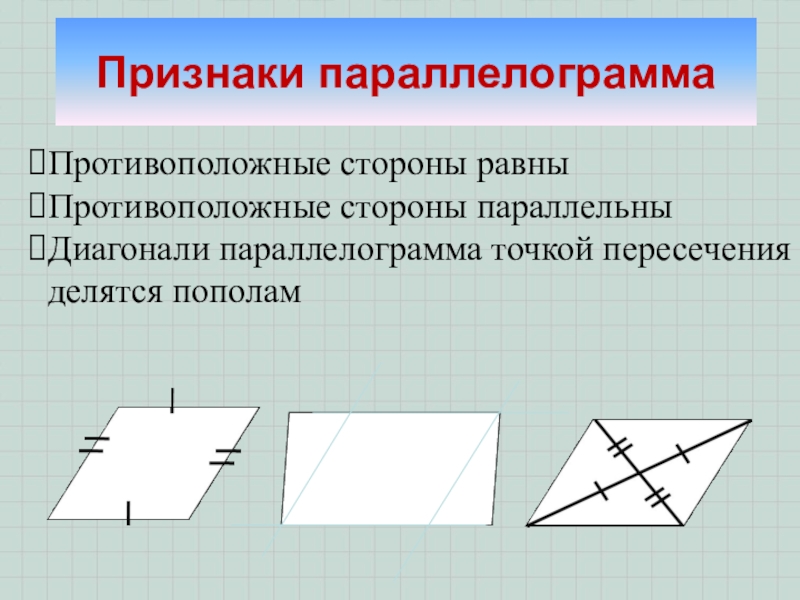
- 13. Признаки параллелограммаПротивоположные стороны равныПротивоположные стороны параллельныДиагонали параллелограмма точкой пересечения делятся пополам
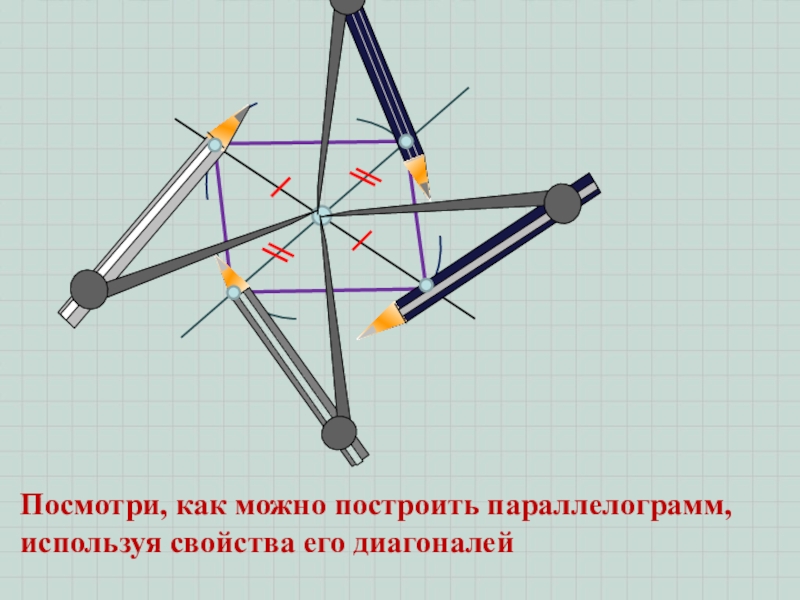
- 14. Посмотри, как можно построить параллелограмм, используя свойства его диагоналей
- 15. Домашнее заданиеЧитать пункт 44; Выучить наизусть признаки с доказательством; Выполнять № 382, 383
Задачи урока:
Слайд 3
А
B
C
D
AB ⎢⎢CD, AC ⎢⎢BD
Вопросы для устного повторения
Какая фигура называется параллелограммом?
Назовите
его элементы?
Перечислите известные свойства параллелограмма
Перечислите известные свойства параллелограмма
Слайд 6 Теоремой, обратной данной, называется теорема, в которой условием является заключение данной
теоремы,
а заключением - условие данной теоремы
Слайд 7Свойство равнобедренного треугольника
В
С
В равнобедренном треугольнике углы при основании
Признак
Если в треугольнике
углы при основании равны, то
А
А
С
равны
треугольник равнобедренный
В
Слайд 8В параллелограмме противоположные стороны равны.
Если в четырехугольнике противоположные стороны равны,
то
этот четырехугольник параллелограмм.
Свойство
Признак
Слайд 92°. Если AB=CD и BC=AD, то ABCD-параллелограмм.
А
B
C
Дано:
ABCD –четырехугольник. AB=CD и BC=AD.
Доказать,
что ABCD-параллелограмм.
D
Слайд 10В параллелограмме диагонали точкой пересечения делятся пополам.
Если в четырехугольнике диагонали точкой
пересечения делятся пополам,
то этот четырехугольник- параллелограмм
то этот четырехугольник- параллелограмм
Слайд 113°. Если ACՈBD = O и BO = OD,AO = OC,
то ABCD-параллелограмм.
А
B
C
D
Дано:
ABCD – четырехугольник. ACՈCD = O
BO=0D, AO=OC.
Доказать, что ABCD-параллелограмм.
O
Слайд 12Если AB=CD и AB||CD, то ABCD-параллелограмм.
А
B
C
D
Дано:
ABCD –четырехугольник. AB=CD и AB||CD.
Доказать, что
ABCD-параллелограмм.
В параллелограмме АBCD противоположные стороны равны и параллельны
Слайд 13Признаки параллелограмма
Противоположные стороны равны
Противоположные стороны параллельны
Диагонали параллелограмма точкой пересечения делятся пополам
Слайд 15Домашнее задание
Читать пункт 44;
Выучить наизусть признаки с доказательством;
Выполнять №
382, 383