информатики
Каширской спецшколы
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Геометрия, 8 класс, Теорема Фалеса
Содержание
- 1. Презентация, Геометрия, 8 класс, Теорема Фалеса
- 2. Теорема ФалесаЕсли параллельные прямые, пересекающие стороны
- 3. Дано:угол;прямые А1В1 ∥ А2В2 ∥ А3В3
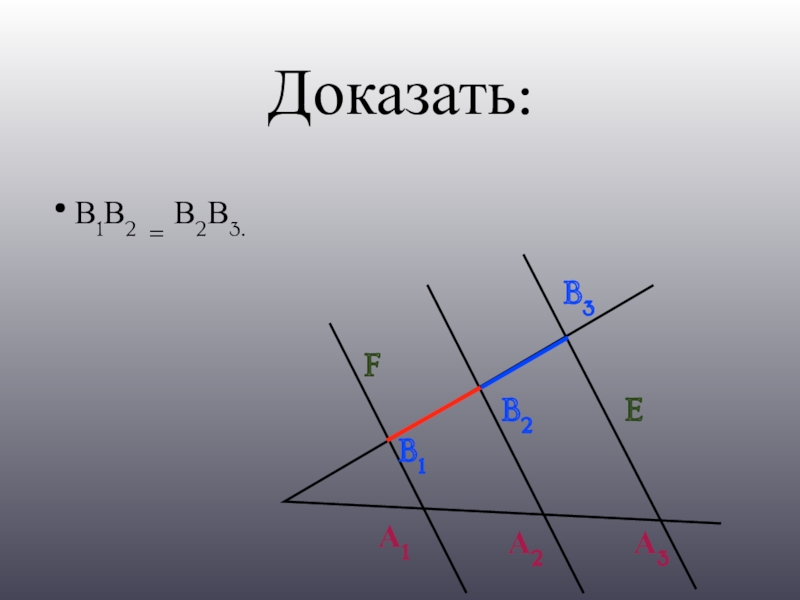
- 4. Доказать:В1В2 = В2В3.А1А2А3B1B2B3FE
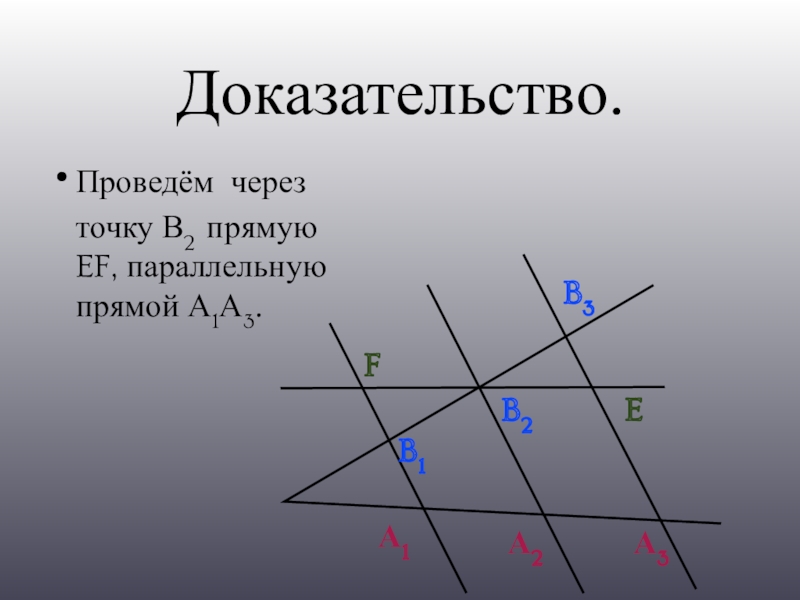
- 5. Доказательство.Проведём через точку В2 прямую EF, параллельную прямой А1А3.А1А2А3B1B2B3FE
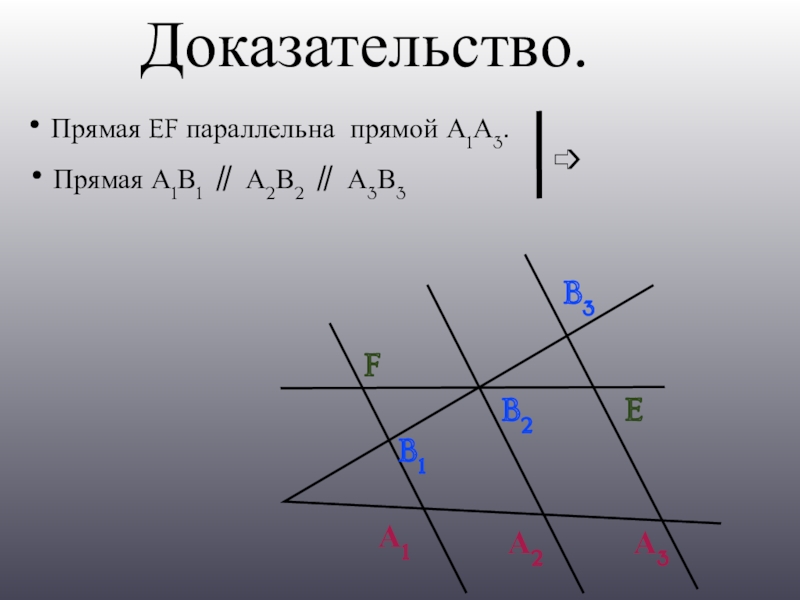
- 6. Доказательство.Прямая EF параллельна прямой А1А3.А1А2А3B1B2B3FE➩Прямая А1В1 ∥ А2В2 ∥ А3В3
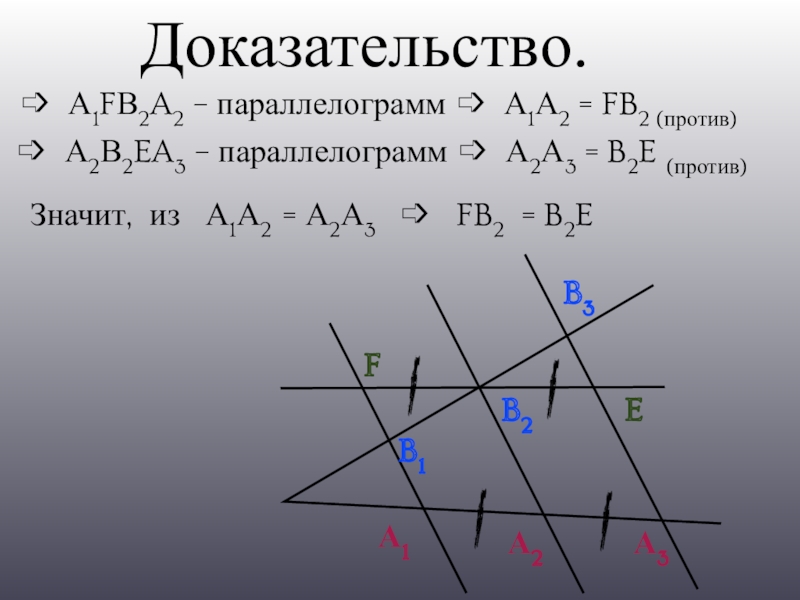
- 7. Доказательство.А1А2А3B1B2B3FE➩ А1FВ2A2 – параллелограмм ➩ А1А2 =
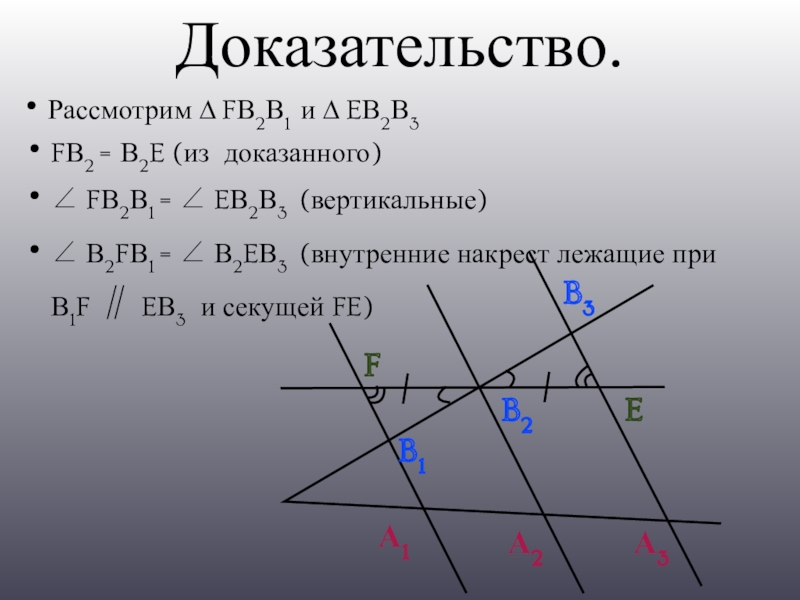
- 8. Доказательство.Рассмотрим ∆ FВ2В1 и ∆ EВ2В3А1А2А3B1B2B3FEFВ2 = В2E (из
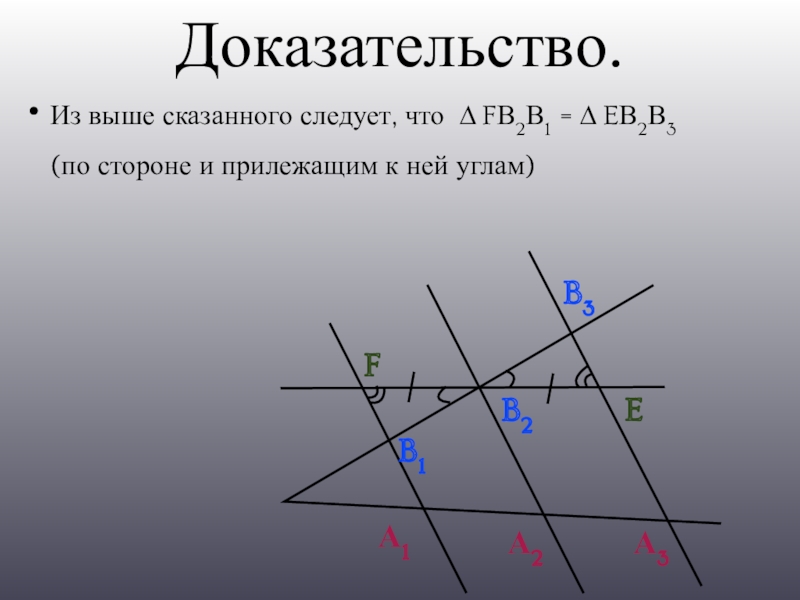
- 9. Доказательство.А1А2А3B1B2B3FEИз выше сказанного следует, что ∆ FВ2В1 = ∆ EВ2В3 (по стороне и прилежащим к ней углам)
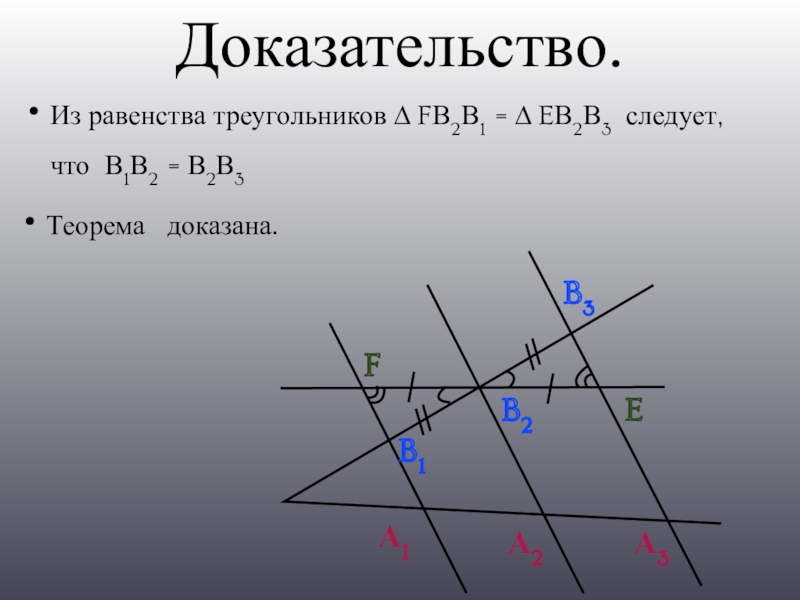
- 10. Доказательство.А1А2А3B1B2B3FEИз равенства треугольников ∆ FВ2В1 = ∆ EВ2В3 следует, что В1В2 = В2В3 Теорема доказана.
- 11. Спасибозавнимание!
Теорема ФалесаЕсли параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Слайд 2Теорема Фалеса
Если параллельные прямые, пересекающие стороны угла, отсекают на одной
его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
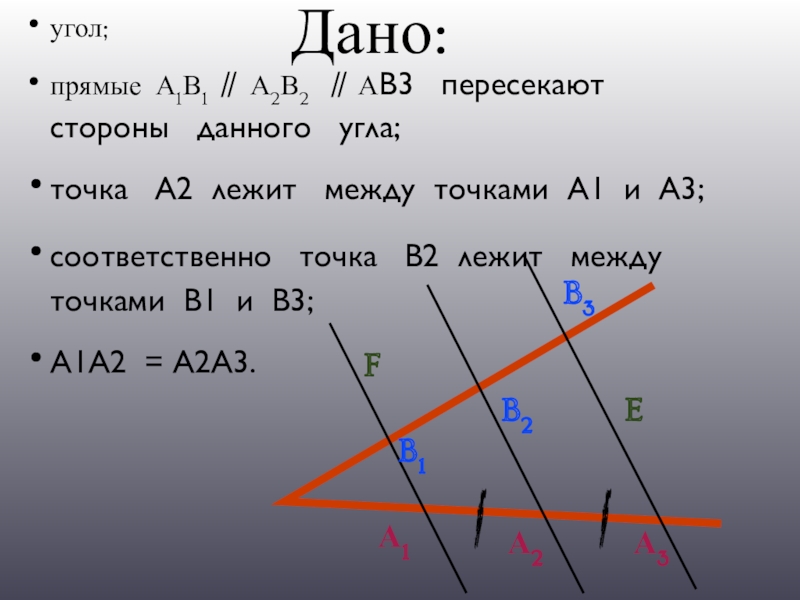
Слайд 3Дано:
угол;
прямые А1В1 ∥ А2В2 ∥ А3В3 пересекают стороны
данного угла;
точка А2 лежит между точками А1 и А3;
соответственно точка В2 лежит между точками В1 и В3;
А1А2 = А2А3.
точка А2 лежит между точками А1 и А3;
соответственно точка В2 лежит между точками В1 и В3;
А1А2 = А2А3.
А1
А2
А3
B1
B2
B3
F
E
Слайд 7Доказательство.
А1
А2
А3
B1
B2
B3
F
E
➩ А1FВ2A2 – параллелограмм ➩ А1А2 = FB2 (против)
➩ А2В2EA3 –
параллелограмм ➩ А2А3 = B2E (против)
Значит, из А1А2 = А2А3 ➩ FB2 = B2E
Слайд 8Доказательство.
Рассмотрим ∆ FВ2В1 и ∆ EВ2В3
А1
А2
А3
B1
B2
B3
F
E
FВ2 = В2E (из доказанного)
∠ FВ2В1 = ∠
EВ2В3 (вертикальные)
∠ В2FВ1 = ∠ В2EВ3 (внутренние накрест лежащие при В1F ∥ EВ3 и секущей FE)
Слайд 9Доказательство.
А1
А2
А3
B1
B2
B3
F
E
Из выше сказанного следует, что ∆ FВ2В1 = ∆ EВ2В3 (по стороне и
прилежащим к ней углам)
Слайд 10Доказательство.
А1
А2
А3
B1
B2
B3
F
E
Из равенства треугольников ∆ FВ2В1 = ∆ EВ2В3 следует, что В1В2 =
В2В3
Теорема доказана.