Презентация, доклад доказательство по математике Пирамида

АВСS – пирамида, (А1В1С1)
пересекает пирамиду АВСS
(А1В1С1) || (АВС)
Доказать: пирамида АВСS пирамиде А1В1С1S
Доказательство: Пусть
Подвергнем пирамиду АВСS гомотетии относительно вершины S с коэффициентом гомотетии k. При этой гомотетии плоскость основания переходит в параллельную плоскость , проходящую через точку А1., т. е. в секущую плоскость, а следовательно вся пирамида - в отсекаемую этой плоскостью часть.
Так как гомотетия есть преобразование подобия , то отсекаемая часть пирамиды является пирамидой, подобной данной.
Теорема доказана.

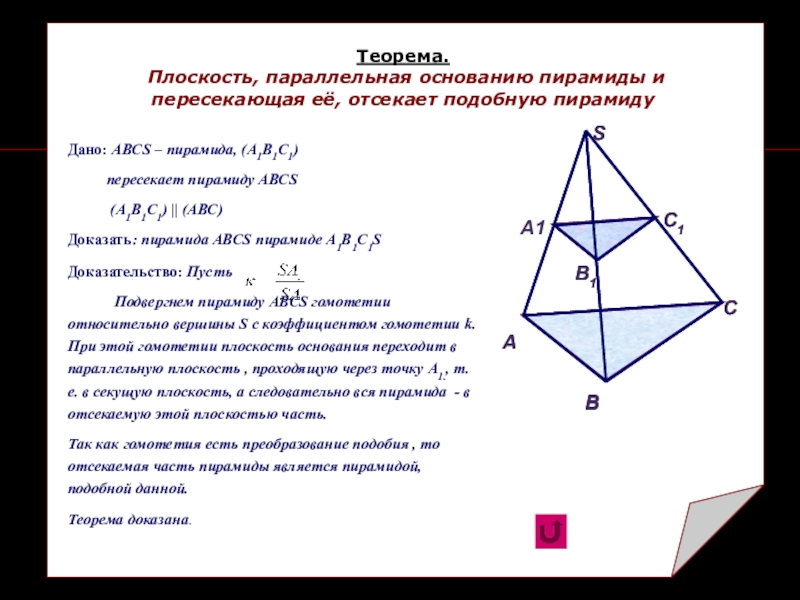
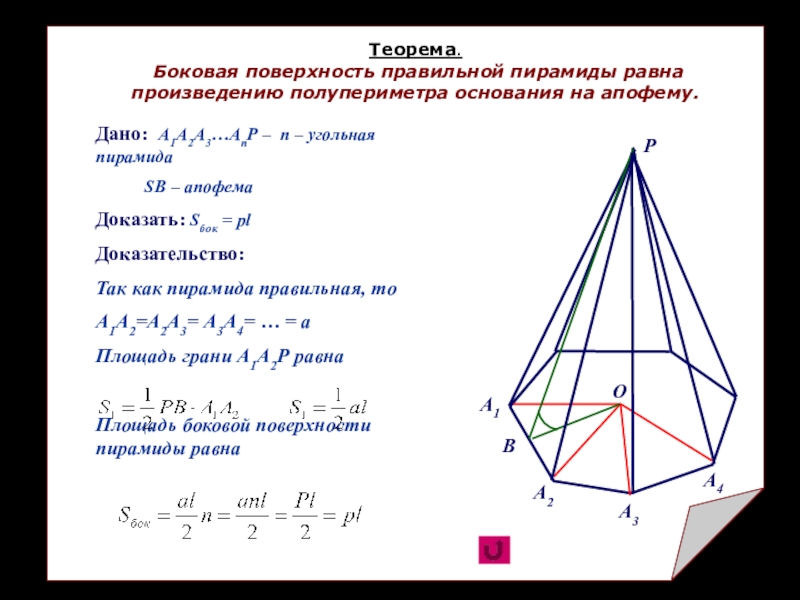
Теорема.
Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает подобную пирамиду

А

В

С

S

A1

В1

С1

А

В

С

S

В1

С1

Дано: АВСS – пирамида, (А1В1С1)
пересекает пирамиду АВСS
(А1В1С1) || (АВС)
Доказать: пирамида АВСS пирамиде А1В1С1S
Доказательство: Пусть
Подвергнем пирамиду АВСS гомотетии относительно вершины S с коэффициентом гомотетии k. При этой гомотетии плоскость основания переходит в параллельную плоскость , проходящую через точку А1., т. е. в секущую плоскость, а следовательно вся пирамида - в отсекаемую этой плоскостью часть.
Так как гомотетия есть преобразование подобия , то отсекаемая часть пирамиды является пирамидой, подобной данной.
Теорема доказана.

А1А2А3…АnР – n – угольная пирамида
SВ – апофема
Доказать: Sбок = рl
Доказательство:
Так как пирамида правильная, то
А1А2=А2А3= А3А4= … = а
Площадь грани А1А2Р равна

Площадь боковой поверхности пирамиды равна

А1

А2

А3

А4

В

О

Р

основания на апофему

Дано:

Дано: А1А2A3…AnB1B2B3 …B n – n-угольная правильная усечённая пирамида l-апофема
Доказать: S бок = (Р1 + Р2 ) · l
Доказательство:
Так как трапеция правильная, боковые грани равные трапеции
Пусть А1А2 = а, В1В2 = в
Площадь одной грани
Площадь всех граней, т. е. площадь боковой поверхности равна