Светлана Владимировна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для проведения урока по геометрии
Содержание
- 1. Презентация для проведения урока по геометрии
- 2. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ. Симметрия относительно точки или
- 3. ОСЕВАЯ СИММЕТРИЯ. Симметрия относительно прямой (или
- 4. ЗЕРКАЛЬНАЯ СИММЕТРИЯТочки А и В называются симметричными
- 5. СИММЕТРИЯ НА ПЛОСКОСТИ Симметрия относительно плоскости - это
- 6. Следует отметить, что две симметричные фигуры или
- 7. Слайд 7
- 8. СИММЕТРИЯ ОТНОСИТЕЛЬНО ТОЧКИТочки А и А1 называются
- 9. СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙДве фигуры называются симметричными относительно
- 10. СИММЕТРИЯ ОТНОСИТЕЛЬНО ПЛОСКОСТИ
- 11. Слайд 11
- 12. Слайд 12
- 13. СКОЛЬЗЯЩАЯ СИММЕТРИЯСкользящая симметрия плоскости – это композиция
- 14. Спасибо за внимание!
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ. Симметрия относительно точки или центральная симметрия - это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону центра симметрии, соответствует другая точка, расположенная по другую сторону центра. При этом точки находятся
Слайд 1СИММЕТРИЯ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
Выполнила
студентка группы СД 12.5
Шамшетдинова Эльмира
Руководитель
Рябухина
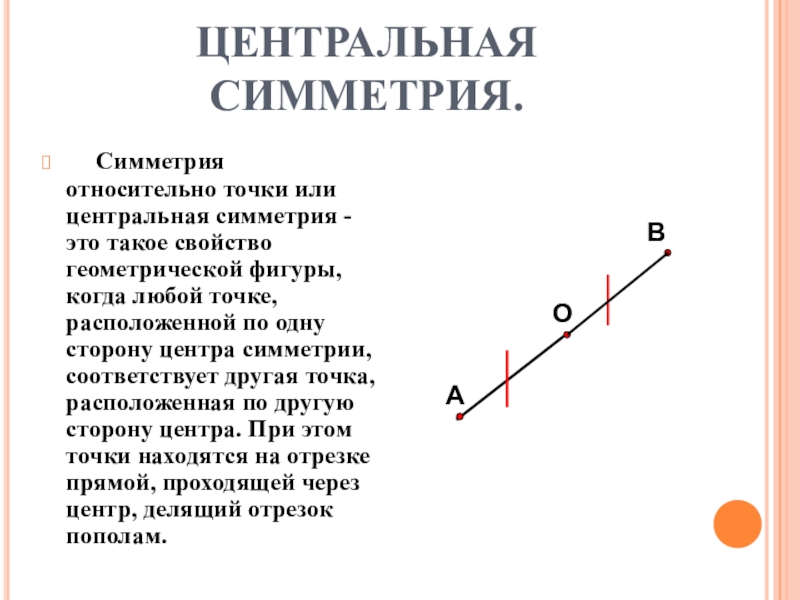
Слайд 2ЦЕНТРАЛЬНАЯ СИММЕТРИЯ.
Симметрия относительно точки или центральная симметрия - это
такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону центра симметрии, соответствует другая точка, расположенная по другую сторону центра. При этом точки находятся на отрезке прямой, проходящей через центр, делящий отрезок пополам.
А
О
В
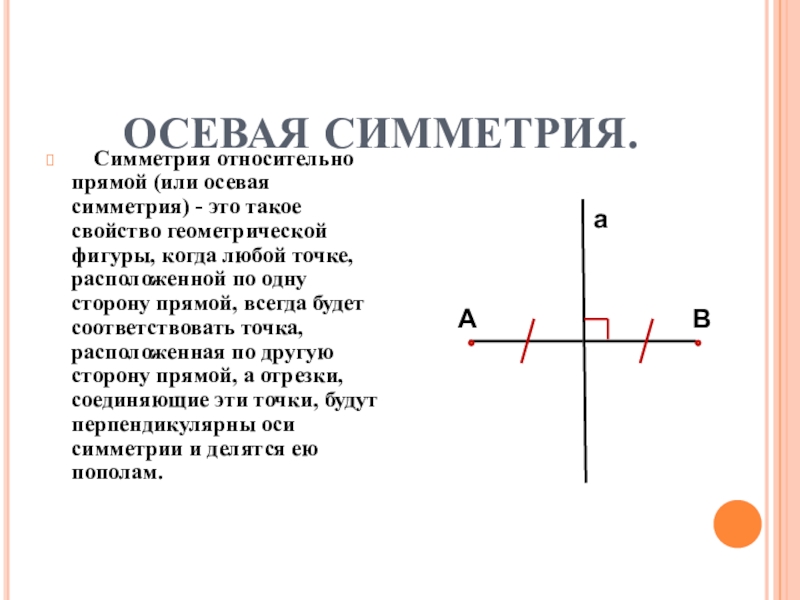
Слайд 3ОСЕВАЯ СИММЕТРИЯ.
Симметрия относительно прямой (или осевая симметрия) - это
такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону прямой, всегда будет соответствовать точка, расположенная по другую сторону прямой, а отрезки, соединяющие эти точки, будут перпендикулярны оси симметрии и делятся ею пополам.
a
А
В
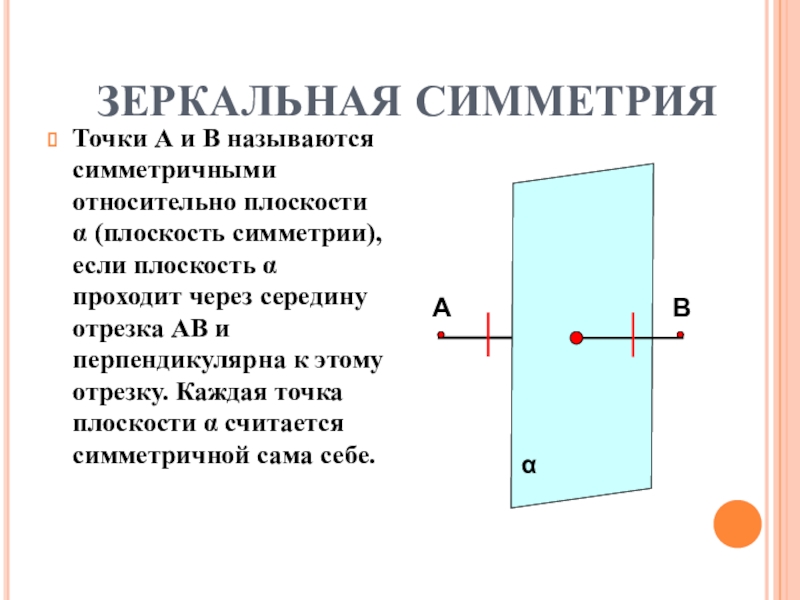
Слайд 4ЗЕРКАЛЬНАЯ СИММЕТРИЯ
Точки А и В называются симметричными относительно плоскости α (плоскость
симметрии), если плоскость α проходит через середину отрезка АВ и перпендикулярна к этому отрезку. Каждая точка плоскости α считается симметричной сама себе.
А
В
α
Слайд 5СИММЕТРИЯ НА ПЛОСКОСТИ
Симметрия относительно плоскости - это такое свойство геометрической фигуры,
когда любой точке, расположенной по одну сторону плоскости, всегда будет соответствовать точка, расположенная по другую сторону плоскости, а отрезки, соединяющие эти точки, будут перпендикулярны плоскости симметрии и делятся ею пополам.
Слайд 6
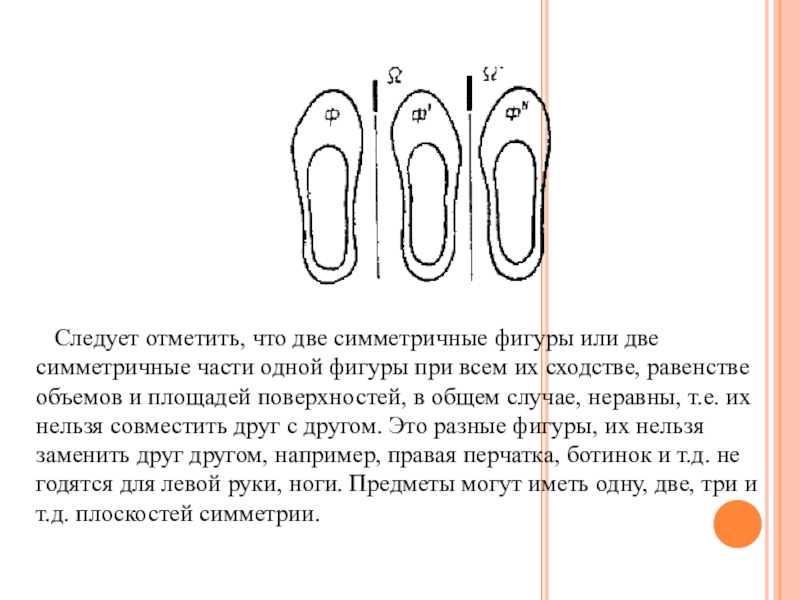
Следует отметить, что две симметричные фигуры или две симметричные части одной
фигуры при всем их сходстве, равенстве объемов и площадей поверхностей, в общем случае, неравны, т.е. их нельзя совместить друг с другом. Это разные фигуры, их нельзя заменить друг другом, например, правая перчатка, ботинок и т.д. не годятся для левой руки, ноги. Предметы могут иметь одну, две, три и т.д. плоскостей симметрии.
Слайд 8СИММЕТРИЯ ОТНОСИТЕЛЬНО ТОЧКИ
Точки А и А1 называются симметричными относительно точки О
(центр симметрии), если О – середина отрезка АА1.
Точка О считается симметричной самой себе.
Симметрия относительно точки называется центральной симметрией
Точка О – центр симметрии
Точка О считается симметричной самой себе.
Симметрия относительно точки называется центральной симметрией
Точка О – центр симметрии
О
А
Слайд 9СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙ
Две фигуры называются симметричными относительно некоторой прямой, если при
перегибании плоскости чертежа по этой прямой они совмещаются.
Прямая, относительно которой данные фигуры симметричны, называется их осью симметрии.
Из определения симметричных фигур следует, что всякие симметричные фигуры равны.
Прямая, относительно которой данные фигуры симметричны, называется их осью симметрии.
Из определения симметричных фигур следует, что всякие симметричные фигуры равны.
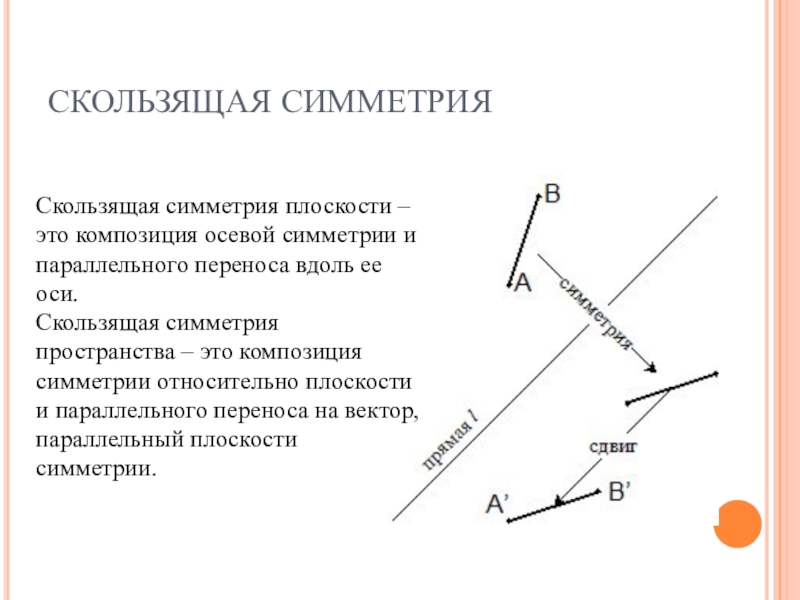
Слайд 13СКОЛЬЗЯЩАЯ СИММЕТРИЯ
Скользящая симметрия плоскости – это композиция осевой симметрии и параллельного
переноса вдоль ее оси.
Скользящая симметрия пространства – это композиция симметрии относительно плоскости и параллельного переноса на вектор, параллельный плоскости симметрии.
Скользящая симметрия пространства – это композиция симметрии относительно плоскости и параллельного переноса на вектор, параллельный плоскости симметрии.