- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для повторения модуля Геометрия при подготовке к ГИА (9 класс)
Содержание
- 1. Презентация для повторения модуля Геометрия при подготовке к ГИА (9 класс)
- 2. Содержание:УглыПараллельные прямыеТреугольникиМногоугольникиПараллелограмм ТрапецияПрямоугольникРомбКвадратОкружность и круг
- 3. Фигура, образованная двумя лучами (стороны угла) с
- 4. Два угла называются смежными, если одна сторона
- 5. Биссектриса – это луч, исходящий из вершины
- 6. Два угла называются вертикальными, если стороны одного
- 7. Решение:∠СОВ и ∠АОС смежные, значит,∠СОВ+∠АОС=180°,∠СОВ=180°–150°=30°Ответ: 30°ЗакреплениеЗадача: Найдите градусную меру угла ∠СОВ, если ∠АОС=150°
- 8. Параллельные прямыеПрямые, которые не пересекаются, называются параллельными.Две
- 9. Прямые и секущаяДве прямые пересеченные третьей, которая
- 10. Признаки параллельности прямыхЕсли при пересечении двух прямых
- 11. ЗакреплениеЗадача: Докажите, что прямые а и в параллельны.Доказательство:∠DEB=∠FEN=120° (как вертикальные углы)⇒∠DEB= ∠АBМ (соответственные) ⇒ а||в
- 12. Серединные перпендикулярСерединным перпендикуляром к отрезку называется прямая,
- 13. Серединные перпендикуляры к сторонам треугольника пересекаются в
- 14. Теорема ФалесаЕсли параллельные прямые, пересекающие стороны угла,
- 15. ТреугольникТреугольником называется многоугольник с тремя углами.∆АВСПериметром треугольника называется сумма длин его сторон.Р∆АВС=АВ+ВС+АС
- 16. Отрезок, соединяющий вершину треугольника с серединой противоположной
- 17. Высота, медиана, биссектриса треугольникаПерпендикуляр, проведенный из вершины
- 18. ЗакреплениеЗадание: Укажите номера верных утверждений:Сумма смежных углов
- 19. ЗакреплениеРешение:Неверно, так как сумма смежных углов равна
- 20. Свойства треугольникаСумма углов треугольника равна 180°.Каждая сторона
- 21. Угол, смежный с каким-нибудь углом треугольника, называется
- 22. Равенство треугольниковРавные треугольники – это такие треугольники,
- 23. Равенство треугольниковII признак. По стороне и прилежащим
- 24. Фигуры, которые имеют различные размеры, но одинаковую форму называются подобными.Признаки подобия треугольниковk – коэффициент подобия.
- 25. Если два угла одного треугольника соответственно равны
- 26. 2. Если две стороны одного треугольника пропорциональны
- 27. 3. Если три стороны одного треугольника пропорциональны
- 28. ЗакреплениеЗадание: Найдите градусную меру ∠С ∆АВС, если ∠А=120°, ∠В=30°.Решение: ∠А+∠ В+∠С=180°, 120°+30° +∠С=180°, ∠С=30°.Ответ: 30°
- 29. ЗакреплениеЗадание: Найдите градусную меру меньшего угла между
- 30. ЗакреплениеЗадание: Найдите сторону А1С1 ∆А1В1С1, если ∠В1А1С1=∠ВАС,
- 31. Прямоугольный треугольник(радиан)Определите в радианах 30°, 60° и 180°
- 32. Прямоугольный треугольникТреугольник называется прямоугольным, если один из
- 33. Соотношение между сторонами и углами прямоугольного треугольникаСинусом
- 34. Значения синуса и косинуса некоторых углов
- 35. ЗакреплениеЗадание: Найдите cos120°.Решение:Т.к. угол 120° смежен с углом 60° (120°+60°=180°), тоОтвет: – 0,5.
- 36. ЗакреплениеЗадание: Найдите сторону АС ∆АВС , если
- 37. Средняя линяя треугольникаСредней линией треугольника называется отрезок,
- 38. Точка пересечения медиан треугольникаМедианы треугольника пересекаются в
- 39. Точка пересечения биссектрис и высот треугольникаБиссектрисы треугольника
- 40. Равнобедренный треугольникТреугольник называется равнобедренным, если две его
- 41. Равносторонний треугольникТреугольник, все стороны которого равны, называется
- 42. ЗакреплениеЗадание: Найдите сторону АС ∆АВС , если
- 43. ЗакреплениеЗадание: Медианы АА1 и ВВ1 ∆АВС пересекаются в точке О. Найдите АО, если АА1=6.Решение:Ответ: 4.
- 44. ЗакреплениеЗадание: Периметр треугольника равен 39. найдите его
- 45. Площадь треугольникаПлощадь треугольника равна половине произведения любой
- 46. Площадь треугольникаПлощадь прямоугольного треугольника равна половине произведения его катетов.
- 47. ЗакреплениеЗадание: Найдите площадь треугольника на рисунке. Решение:∆АВС
- 48. ЗакреплениеЗадание: Найдите площади треугольников изображенных на клетчатой бумаге с размером клетки 1?1 на рисунке.
- 49. ЗакреплениеРешение:а) б) в)Ответ: а) 7,5 б) 14 в) 9
- 50. ЗакреплениеЗадание: Найдите площадь ∆АВС, изображенного на рисунке.
- 51. МногоугольникиСумма углов выпуклого n-угольника равна (n-2)·180°Правильным многоугольником
- 52. ПараллелограммПараллелограмм – это четырехугольник, у которого противоположные
- 53. ПараллелограммПлощадь параллелограмма равна произведению двух его сторон на синус угла между ними. SABCD=АВ·АD·sin∠BAD
- 54. Свойства параллелограммаСвойства:Сумма углов параллелограмма равна 360°.∠А+∠B+∠C+∠D=360°2. В
- 55. Признаки параллелограммаПризнаки: Если в четырехугольнике две сторон
- 56. ЗакреплениеЗадание: В четырехугольнике АВСD, АВ=СD=5, ∠DBA=∠CDB=30°. Найдите
- 57. ТрапецияТрапеция – это четырехугольник, у которого две
- 58. ТрапецияПлощадь трапеции равна полусумме оснований умноженной на
- 59. ТрапецияТрапеция называется равнобедренной, если ее боковые стороны
- 60. ЗакреплениеЗадание: Найдите площадь трапеции на рисунке.Решение:ВСЕF –
- 61. ПрямоугольникПрямоугольник – это параллелограмм, у которого все
- 62. Ромб Ромб – это четырехугольник, все стороны
- 63. КвадратКвадрат– это такой прямоугольник, у которого все
- 64. ЗакреплениеЗадание: Найдите площадь и высоту ромба ABCD, изображенного на рисунке.Решение:ВD=2·BO=2·6=12AC=2·AO=2·8=16 (по свойству диагоналей)SABCD=АD·CH 96=10·CH CH=96:10=9,6Ответ: 96; 9,6.
- 65. ЗакреплениеЗадание: Укажите номера верных утверждений.В равностороннем треугольнике
- 66. ЗакреплениеРешение:Неверно, т.к. в равностороннем треугольнике все углы
- 67. Окружность и кругОкружностью называется геометрическая фигура, состоящая
- 68. Окружность и кругЛюбые две точки окружности делят
- 69. Взаимное расположение прямой и окружностиОкружность и прямая
- 70. Взаимное расположение двух окружностейДве окружности могут иметь:
- 71. Взаимное расположение двух окружностейЕсли две окружности касаются,
- 72. Длина окружности и площадь кругаR – радиус
- 73. Углы связанные с окружностьюУгол с вершиной в
- 74. Углы связанные с окружностьюВписанные углы, опирающиеся на
- 75. Углы связанные с окружностьюУгол между пересекающимися хордами
- 76. Углы связанные с окружностьюУгол между касательной и
- 77. Длина дуги и площадь сектораЕсли величина центрального
- 78. Длина дуги и площадь сектораКруговым сектором (или
- 79. ЗакреплениеВ окружности с центром О. Найдите градусную
- 80. Треугольник и окружностьВписанная окружность.Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник
- 81. Треугольник и окружностьОписанная окружность.Серединные перпендикуляры к сторонам
- 82. Треугольник и окружностьПлощадь треугольника равна произведению его
- 83. Треугольник и окружностьЕсли ∆АВС вписан в окружность
- 84. ЗакреплениеНа рисунке окружность с центром в точке
- 85. Четырехугольник и окружностьВ любом описанном четырехугольнике суммы
- 86. Четырехугольник и окружностьВ любом вписанном четырехугольнике сумма
- 87. Многоугольники и окружностьВ любой правильный многоугольник можно вписать окружность.Вокруг любого правильного многоугольника можно описать окружность.
- 88. ЗакреплениеОколо четырехугольника описана окружность. Найдите величину ∠А
Слайд 1Подготовка к ГИА
модуль «Геометрия»
МБОУ «Базовая Павловская СОШ»
Учитель математики
Найданова Д.Р.
Слайд 2Содержание:
Углы
Параллельные прямые
Треугольники
Многоугольники
Параллелограмм
Трапеция
Прямоугольник
Ромб
Квадрат
Окружность и круг
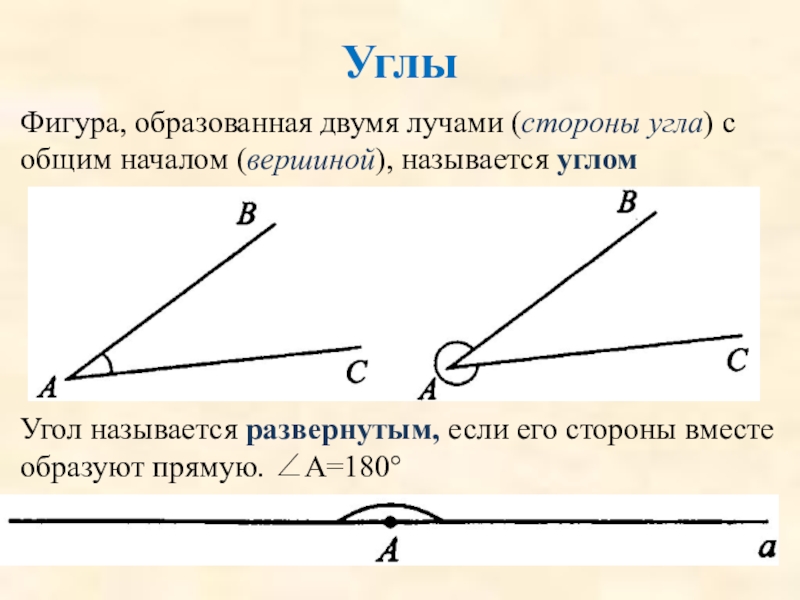
Слайд 3Фигура, образованная двумя лучами (стороны угла) с общим началом (вершиной), называется
Углы
Угол называется развернутым, если его стороны вместе образуют прямую. ∠А=180°
Слайд 4Два угла называются смежными, если одна сторона у них общая, а
∠СОВ+ ∠ ВОА=180°
Смежные углы
Угол равный своему смежному, называется прямым.
∠АВD=∠ DВС=90°
DВ⊥АС
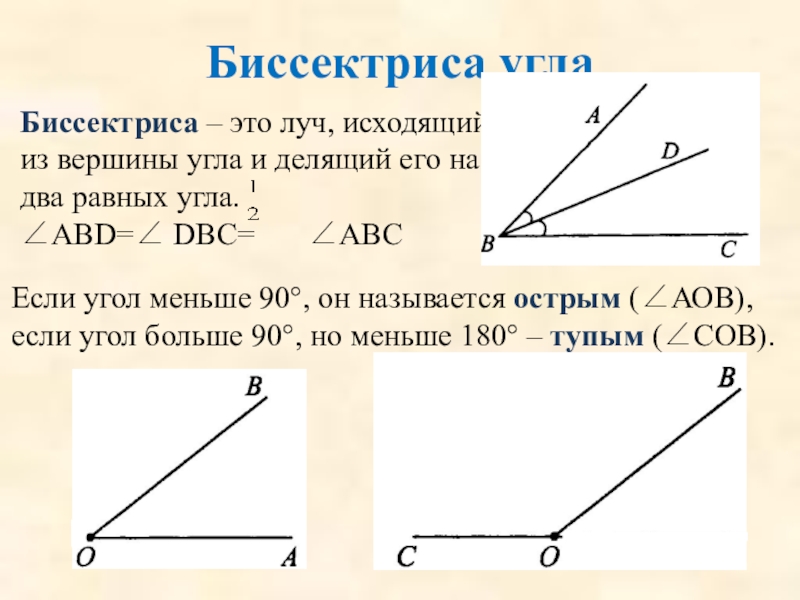
Слайд 5Биссектриса – это луч, исходящий из вершины угла и делящий его
∠АВD=∠ DВС= ∠АВС
Биссектриса угла
Если угол меньше 90°, он называется острым (∠АОВ),
если угол больше 90°, но меньше 180° – тупым (∠СОВ).
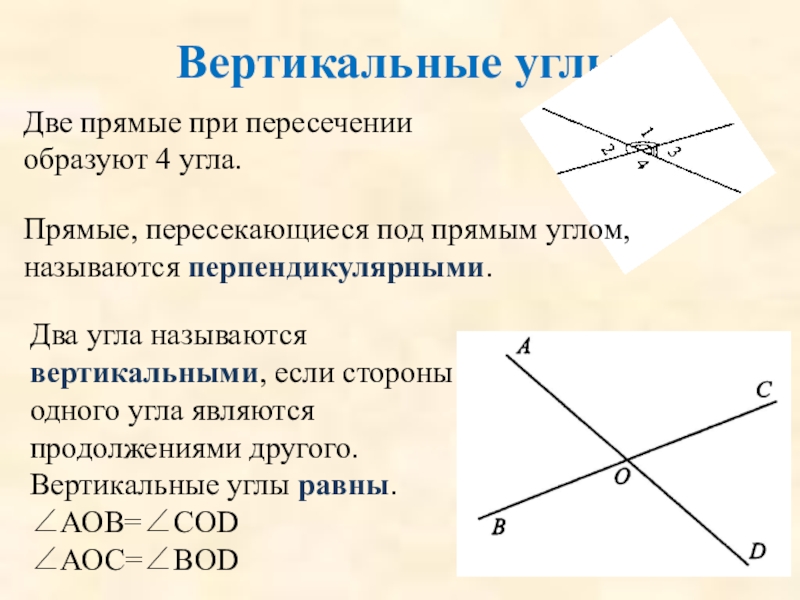
Слайд 6Два угла называются вертикальными, если стороны одного угла являются продолжениями другого.
Вертикальные углы равны.
∠АОВ=∠СОD
∠АОС=∠ВОD
Вертикальные углы
Две прямые при пересечении образуют 4 угла.
Прямые, пересекающиеся под прямым углом, называются перпендикулярными.
Слайд 7Решение:
∠СОВ и ∠АОС смежные, значит,
∠СОВ+∠АОС=180°,
∠СОВ=180°–150°=30°
Ответ: 30°
Закрепление
Задача: Найдите градусную меру угла ∠СОВ,
Слайд 8Параллельные прямые
Прямые, которые не пересекаются, называются параллельными.
Две прямые, перпендикулярные одной и
а⊥с и в⊥с, значит, а||в
Две прямые, параллельные третьей, так же параллельны.
а||в и в||с, то а||с.
Если точка А не лежит на прямой а, то можно провести ровно одну прямую в, проходящую через точку А и параллельную прямой а.
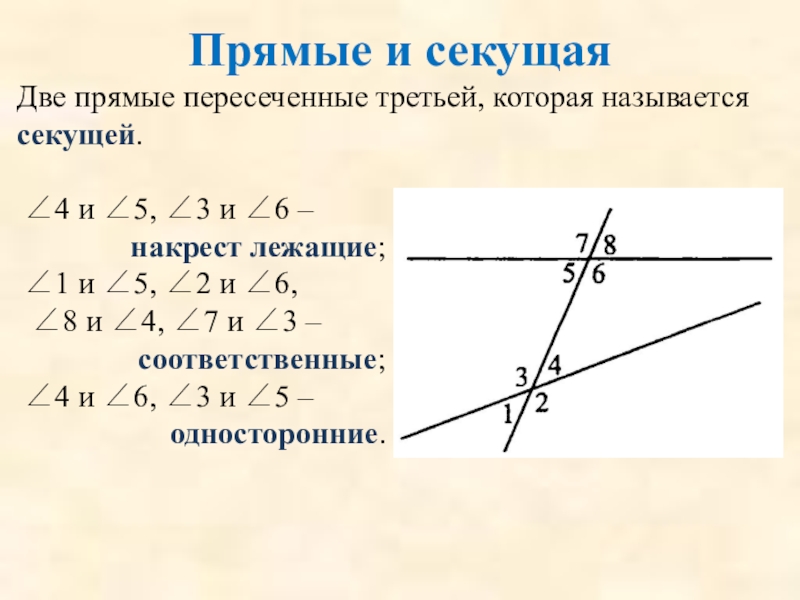
Слайд 9Прямые и секущая
Две прямые пересеченные третьей, которая называется секущей.
∠4 и ∠5,
накрест лежащие;
∠1 и ∠5, ∠2 и ∠6, ∠8 и ∠4, ∠7 и ∠3 –
соответственные;
∠4 и ∠6, ∠3 и ∠5 –
односторонние.
Слайд 10Признаки параллельности прямых
Если при пересечении двух прямых секущей накрест лежащие углы
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Если при пересечении двух прямых секущей сумма односторонних углов равна 180 градусов.
Верно и обратное.
Слайд 11Закрепление
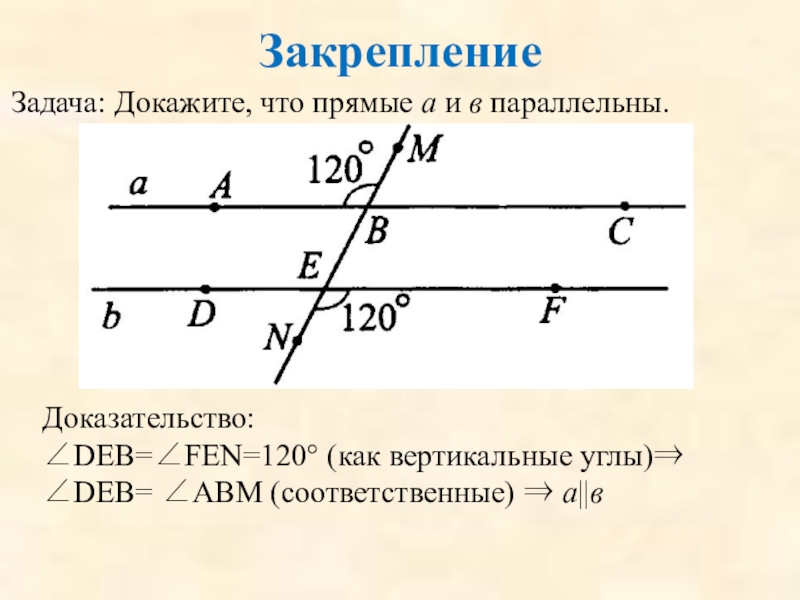
Задача: Докажите, что прямые а и в параллельны.
Доказательство:
∠DEB=∠FEN=120° (как вертикальные углы)⇒
∠DEB=
Слайд 12Серединные перпендикуляр
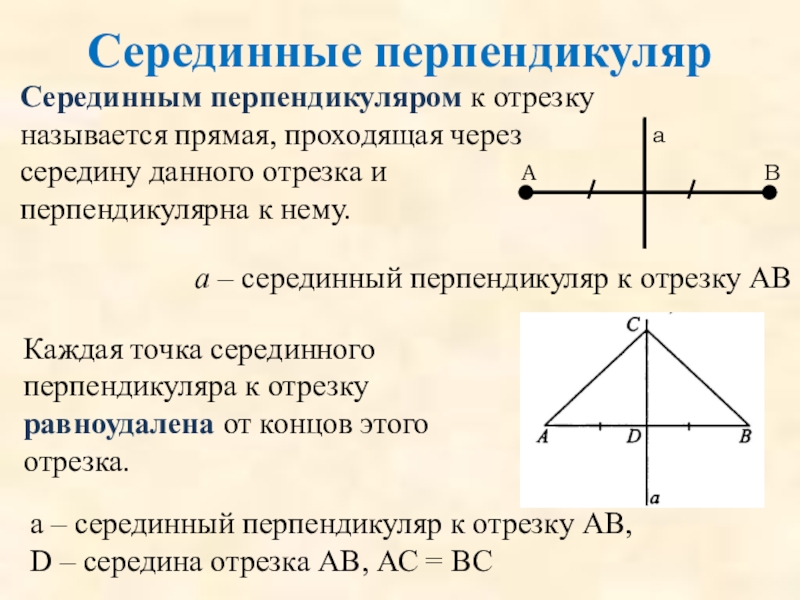
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного
а – серединный перпендикуляр к отрезку АВ
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
а – серединный перпендикуляр к отрезку АВ,
D – середина отрезка АВ, АС = ВС
Слайд 13Серединные перпендикуляры к сторонам треугольника
пересекаются в одной точке
m, n, p
Точка пересечения серединных перпендикуляров
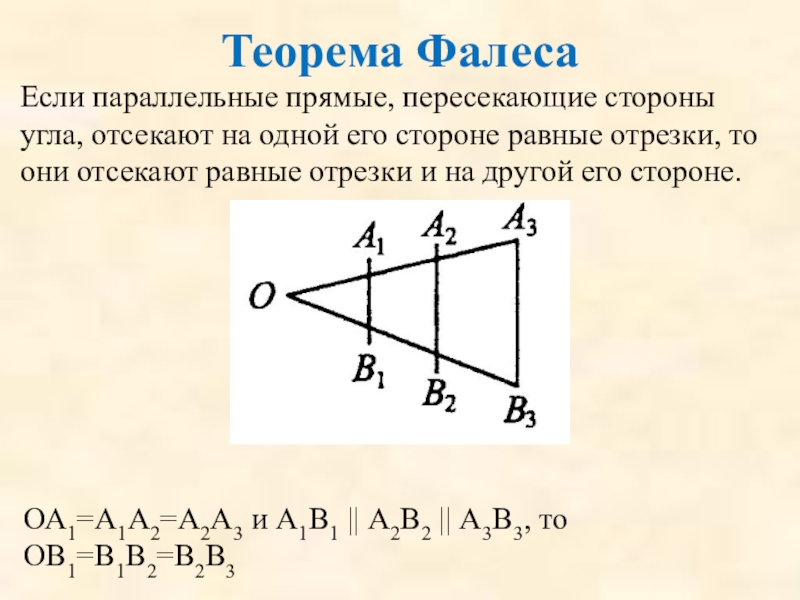
Слайд 14Теорема Фалеса
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его
ОА1=А1А2=А2А3 и А1В1 || А2В2 || А3В3, то
ОВ1=В1В2=В2В3
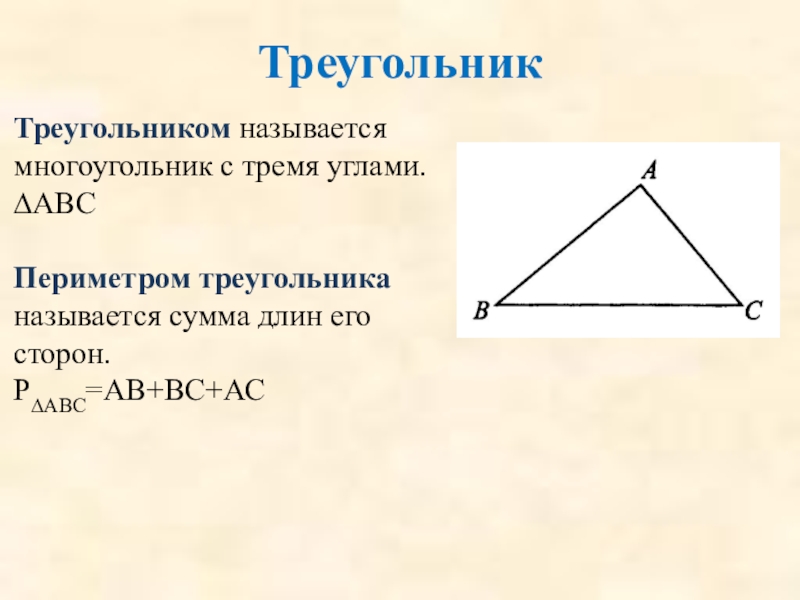
Слайд 15Треугольник
Треугольником называется многоугольник с тремя углами.
∆АВС
Периметром треугольника называется сумма длин его
Р∆АВС=АВ+ВС+АС
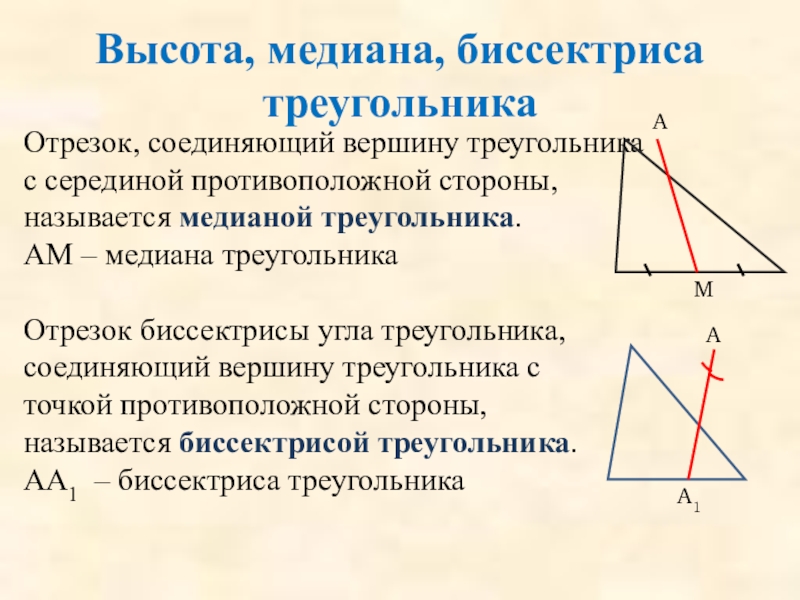
Слайд 16Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
АМ
Высота, медиана, биссектриса треугольника
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
АА1 – биссектриса треугольника
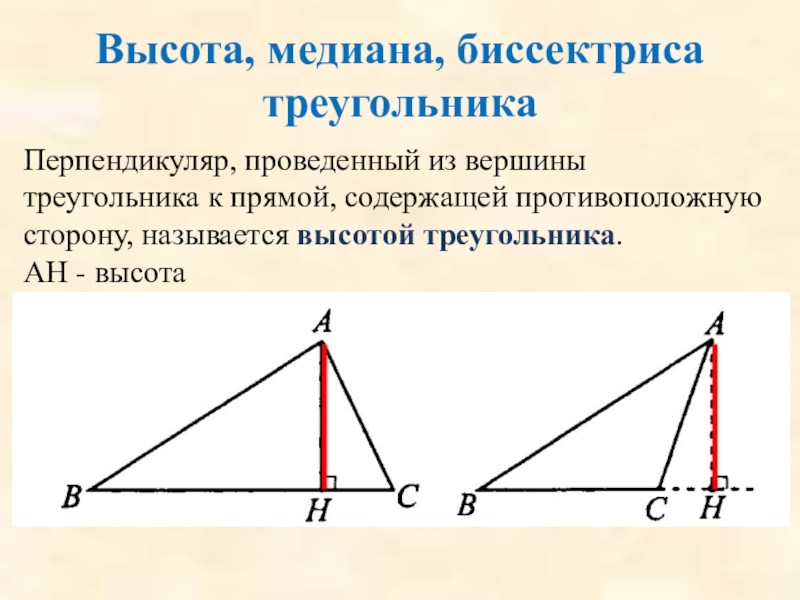
Слайд 17Высота, медиана, биссектриса треугольника
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей
АН - высота
Слайд 18Закрепление
Задание: Укажите номера верных утверждений:
Сумма смежных углов равна 90°.
При пересечении параллельных
Вертикальные углы равны.
Развернутый угол, меньше 90°.
Если точки А1, А2 лежат на одной стороне угла ∠В2ОА2, а точки В1, В2 – на другой, А1В1 || А2В2 и ОА1=А1А2, то В1В2=2ОВ1
Слайд 19Закрепление
Решение:
Неверно, так как сумма смежных углов равна 180°.
Верно, так как является
Верно, так как свойство вертикальных углов.
Неверно, так как развернутый угол равен 180°.
Неверно, так как В1В2=ОВ1
Ответ: 23
Слайд 20Свойства треугольника
Сумма углов треугольника равна 180°.
Каждая сторона треугольника меньше суммы двух
Против большей стороны треугольника лежит больший угол.
Против большего угла треугольника лежит большая сторона
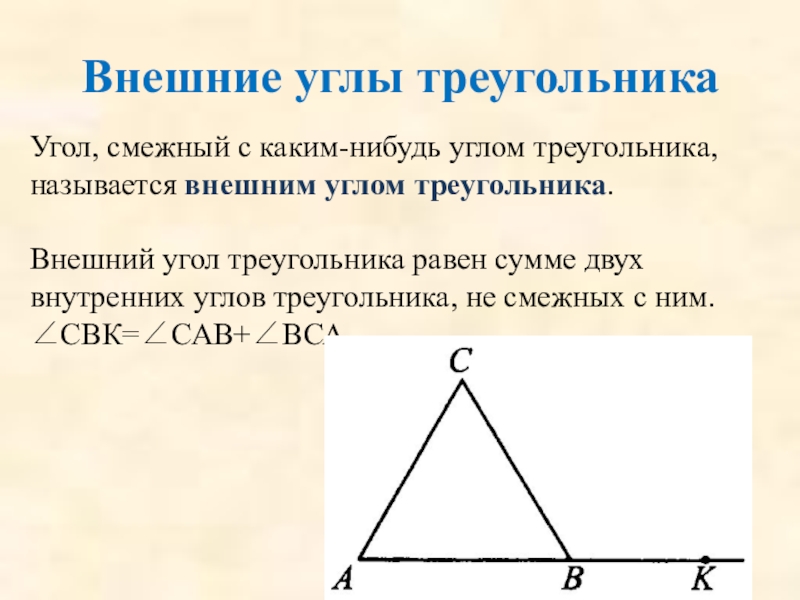
Слайд 21Угол, смежный с каким-нибудь углом треугольника, называется внешним углом треугольника.
Внешний угол
∠СВК=∠САВ+∠ВСА
Внешние углы треугольника
Слайд 22Равенство треугольников
Равные треугольники – это такие треугольники, которые можно совместить друг
I признак. По двум сторонам и углу между ними
А
N
М
К
С
В
Если ∠A = ∠ K,
AB = KM,
AC = KN,
то ∆ABC = ∆KMN
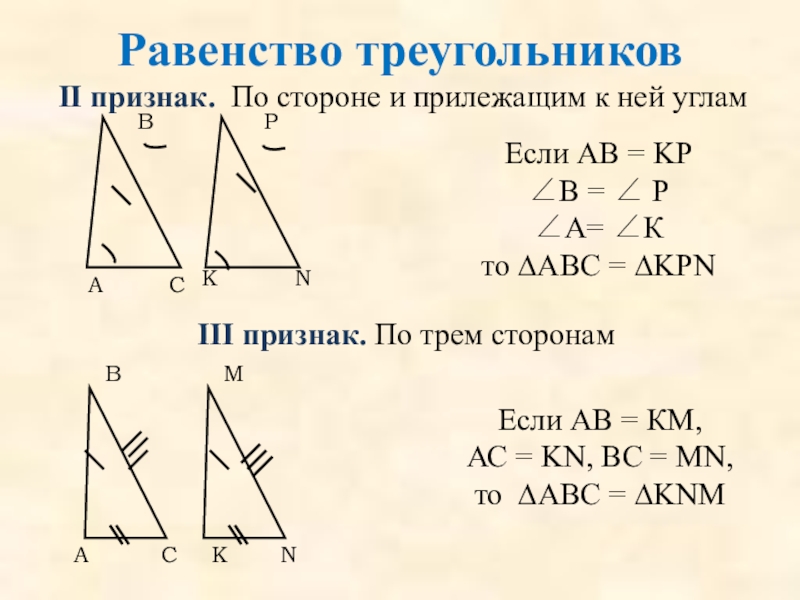
Слайд 23Равенство треугольников
II признак. По стороне и прилежащим к ней углам
А
C
B
P
N
К
Если AB
∠B = ∠ P
∠А= ∠К
то ∆ABC = ∆KPN
III признак. По трем сторонам
А
C
B
M
K
N
Если АВ = КМ,
АС = KN, BC = MN,
то ∆АВС = ∆KNM
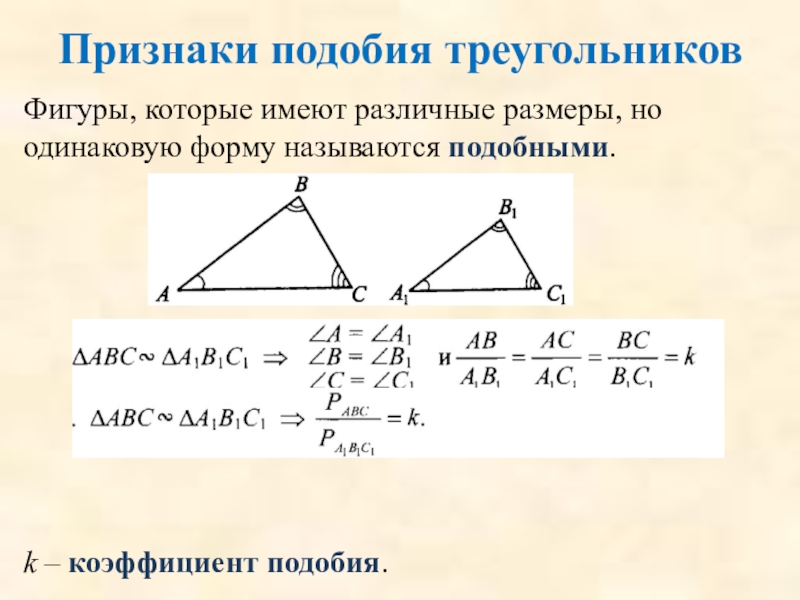
Слайд 24Фигуры, которые имеют различные размеры, но одинаковую форму называются подобными.
Признаки подобия
k – коэффициент подобия.
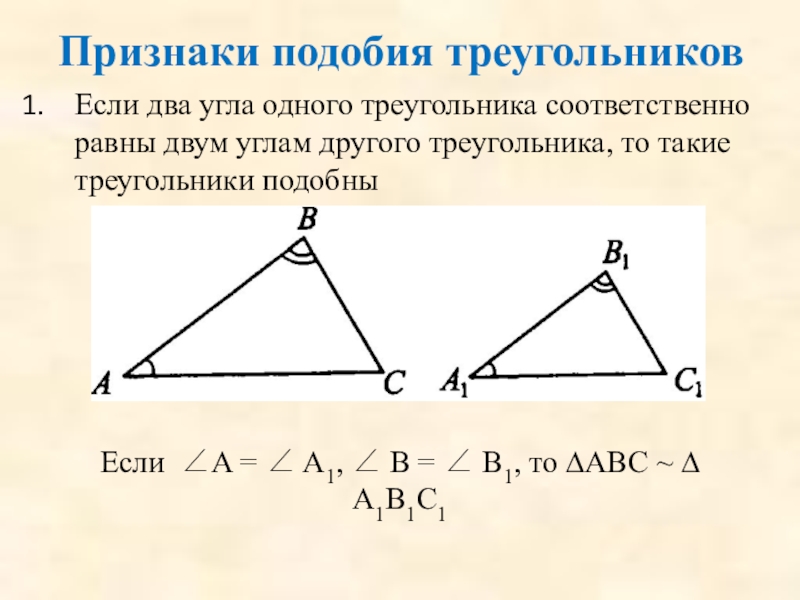
Слайд 25Если два угла одного треугольника соответственно равны двум углам другого треугольника,
Если ∠A = ∠ A1, ∠ B = ∠ В1, то ∆АВС ~ ∆ А1В1С1
Признаки подобия треугольников
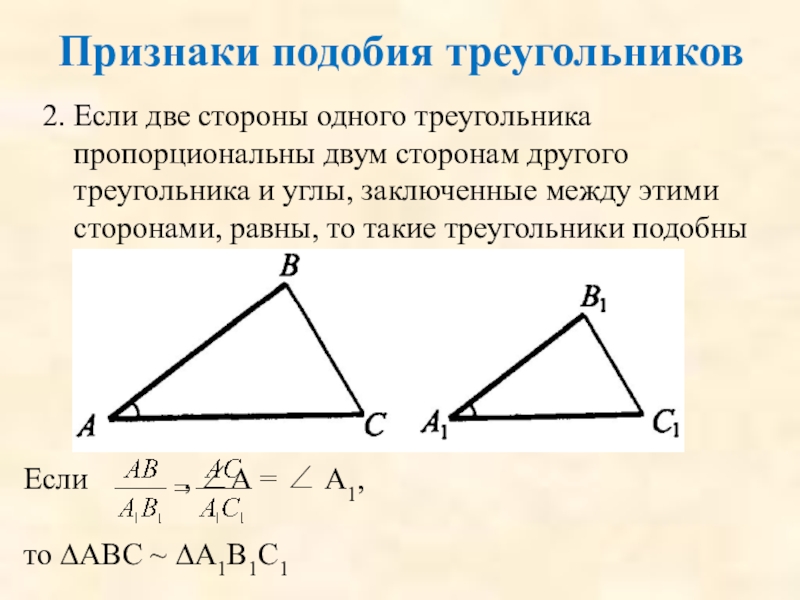
Слайд 262. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника
Если , ∠А = ∠ А1,
то ∆АВС ~ ∆А1В1С1
Признаки подобия треугольников
Слайд 273. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника,
Если ∆АВС ~ ∆А1В1С1
Признаки подобия треугольников
Слайд 28Закрепление
Задание: Найдите градусную меру ∠С ∆АВС, если ∠А=120°, ∠В=30°.
Решение:
∠А+∠ В+∠С=180°,
120°+30° +∠С=180°,
∠С=30°.
Ответ: 30°
Слайд 29Закрепление
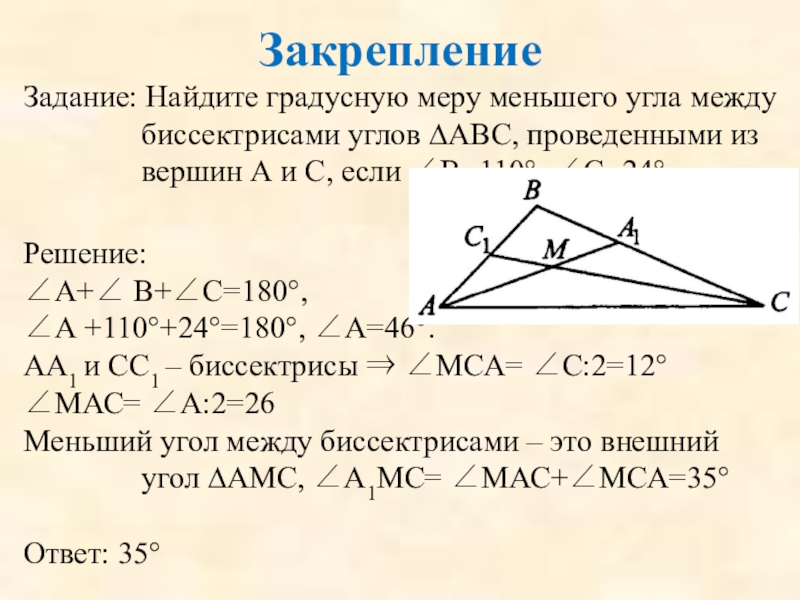
Задание: Найдите градусную меру меньшего угла между биссектрисами углов ∆АВС, проведенными
Решение:
∠А+∠ В+∠С=180°,
∠А +110°+24°=180°, ∠А=46°.
АА1 и СС1 – биссектрисы ⇒ ∠МСА= ∠С:2=12°
∠МАС= ∠А:2=26
Меньший угол между биссектрисами – это внешний угол ∆АМС, ∠А1МС= ∠МАС+∠МСА=35°
Ответ: 35°
Слайд 30Закрепление
Задание: Найдите сторону А1С1 ∆А1В1С1, если ∠В1А1С1=∠ВАС, ∠В1С1А1=∠ ВСА, АС=10, В1С1=4,
Решение:
∠В1А1С1=∠ВАС, ∠В1С1А1=∠ ВСА (по условию) ⇒∆АВС ~ ∆А1В1С1 (по двум углам)
⇒
Ответ: 5.
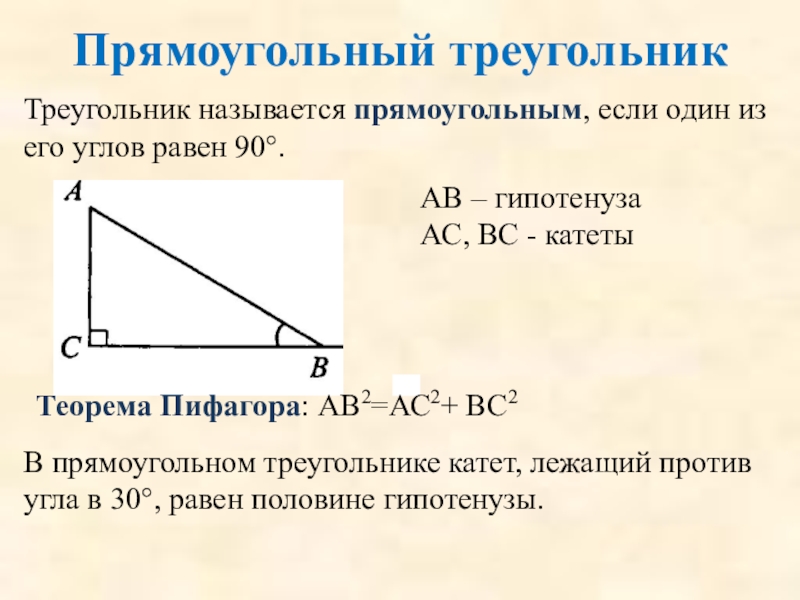
Слайд 32Прямоугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90°.
АВ
АС, ВС - катеты
Теорема Пифагора: АВ2=АС2+ ВС2
В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы.
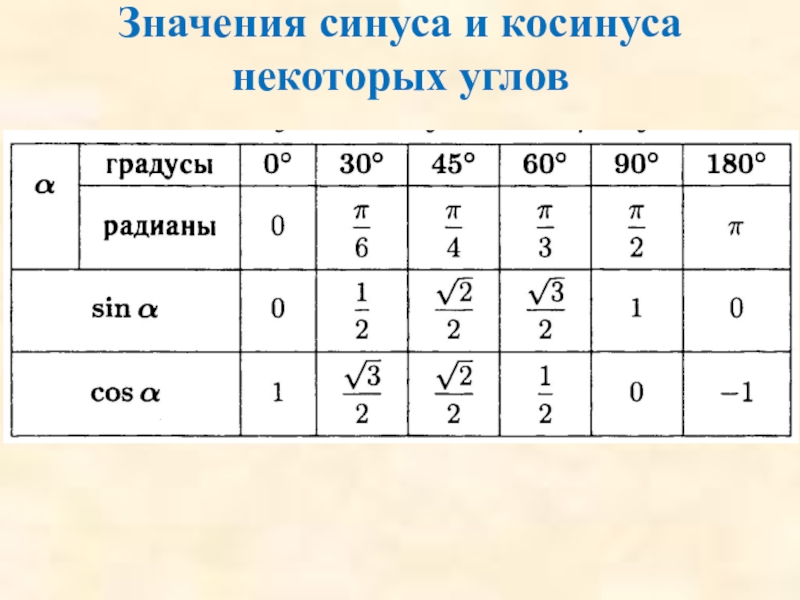
Слайд 33Соотношение между сторонами и углами прямоугольного треугольника
Синусом острого угла прямоугольного треугольника
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему
Слайд 35Закрепление
Задание: Найдите cos120°.
Решение:
Т.к. угол 120° смежен с углом 60° (120°+60°=180°), то
Ответ:
Слайд 36Закрепление
Задание: Найдите сторону АС ∆АВС , если ∠АВС=90°, АВ=5, ВС=4.
Решение:
По теореме
АС2=АВ2 – ВС2
Ответ: 3.
Слайд 37Средняя линяя треугольника
Средней линией треугольника называется отрезок, соединяющий середины двух его
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
МN – средняя линия
MN||AC
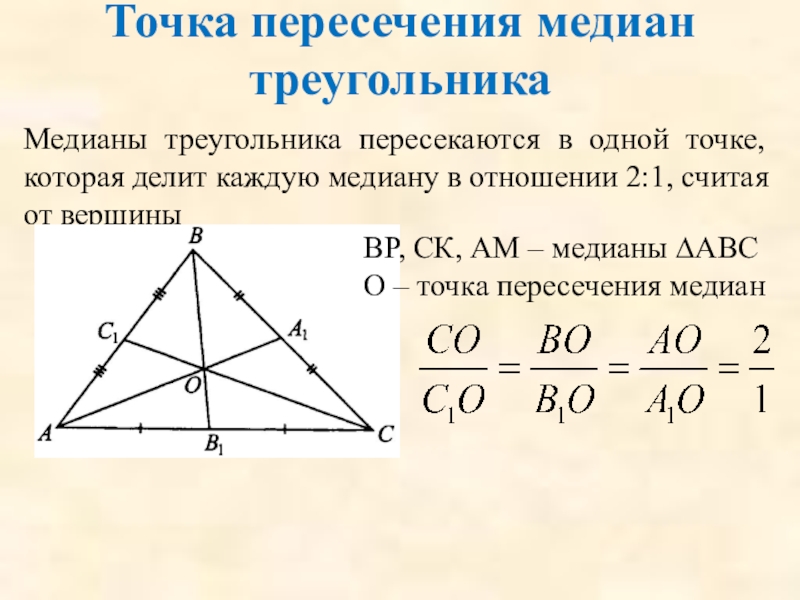
Слайд 38Точка пересечения медиан треугольника
Медианы треугольника пересекаются в одной точке, которая делит
ВР, СК, АМ – медианы ∆АВС
О – точка пересечения медиан
Слайд 39Точка пересечения биссектрис и высот треугольника
Биссектрисы треугольника пересекаются в одной точке
Высоты
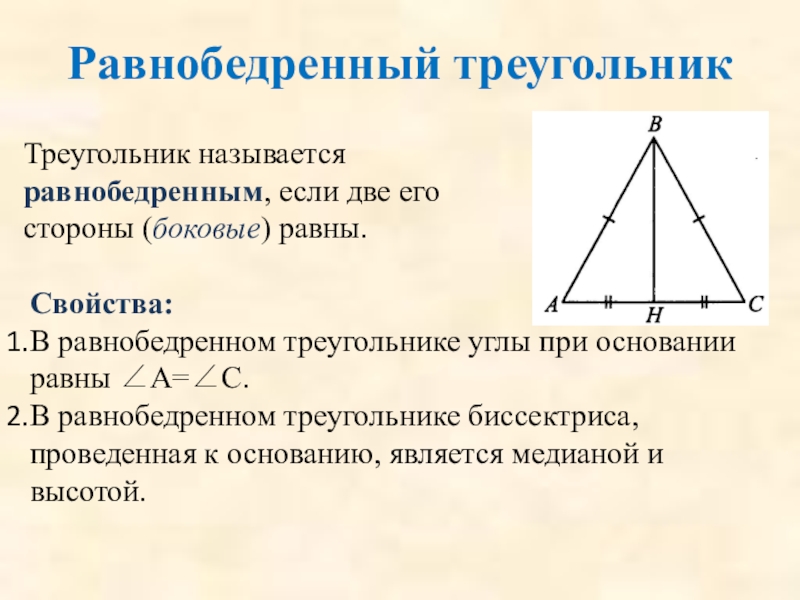
Слайд 40Равнобедренный треугольник
Треугольник называется равнобедренным, если две его стороны (боковые) равны.
Свойства:
В равнобедренном
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Слайд 41Равносторонний треугольник
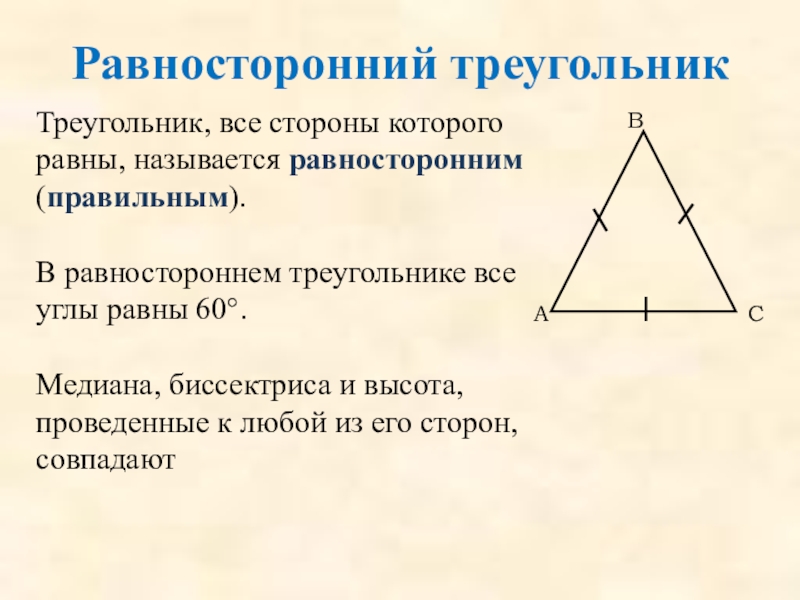
Треугольник, все стороны которого равны, называется равносторонним (правильным).
В равностороннем треугольнике
Медиана, биссектриса и высота, проведенные к любой из его сторон, совпадают
Слайд 42Закрепление
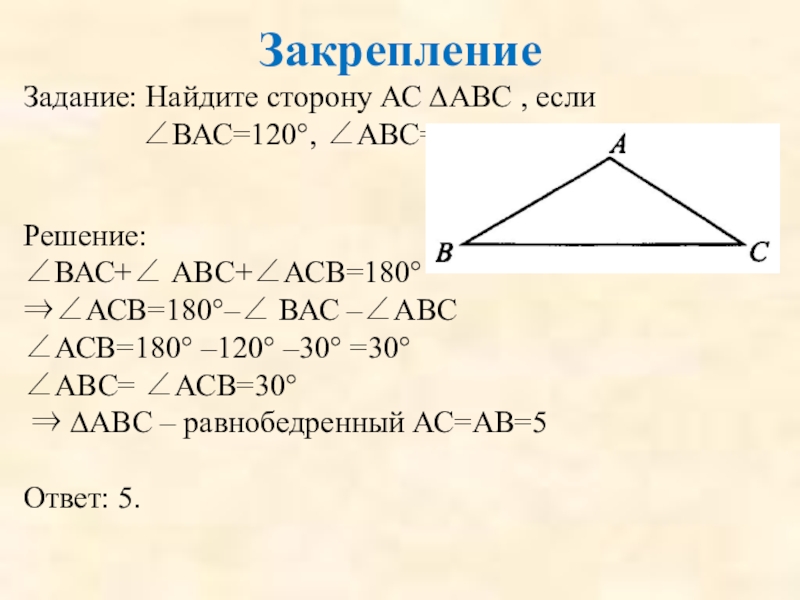
Задание: Найдите сторону АС ∆АВС , если ∠ВАС=120°, ∠АВС=30° АВ=5.
Решение:
∠ВАС+∠ АВС+∠АСВ=180°
⇒∠АСВ=180°–∠ ВАС –∠АВС
∠АСВ=180° –120° –30° =30°
∠АВС= ∠АСВ=30°
⇒ ∆АВС – равнобедренный АС=АВ=5
Ответ: 5.
Слайд 43Закрепление
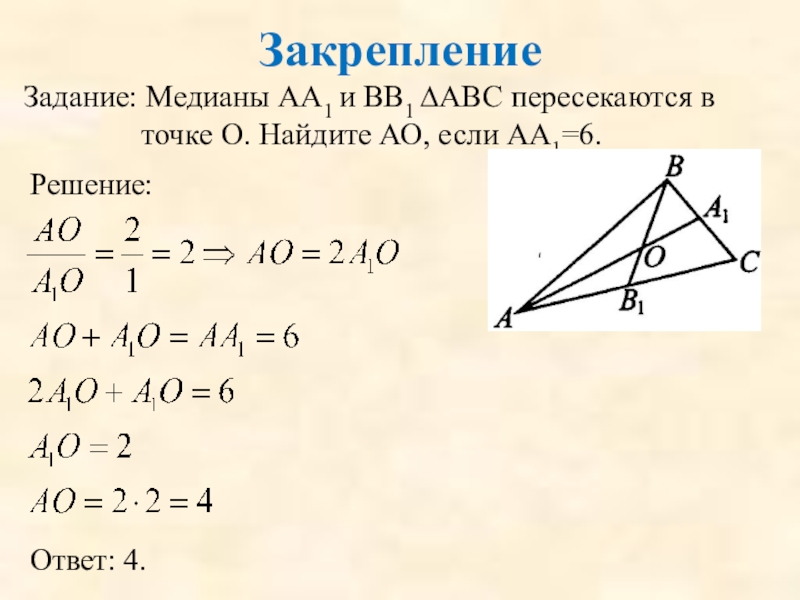
Задание: Медианы АА1 и ВВ1 ∆АВС пересекаются в точке О. Найдите
Решение:
Ответ: 4.
Слайд 44Закрепление
Задание: Периметр треугольника равен 39. найдите его стороны, если стороны подобного
Решение:
∆АВС~∆А1В1С1 по условию ⇒ k–коэффициент подобия
Тогда стороны равны 3k, 4k и 6k.
Р= 3k+4k+6k=39
13k=39
k=3 – коэффициент подобия
3·3=9
4·3=12
6·3=18
Ответ:9, 12, 18.
Слайд 45Площадь треугольника
Площадь треугольника равна половине произведения любой его стороны на высоту,
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Треугольники с равной площадью называются равновеликими.
Слайд 46Площадь треугольника
Площадь прямоугольного треугольника равна половине произведения его катетов.
Слайд 47Закрепление
Задание: Найдите площадь треугольника на рисунке.
Решение:
∆АВС – прямоугольный.
По теореме
ВС2=АВ2 –АС2
Ответ: 6.
Слайд 48Закрепление
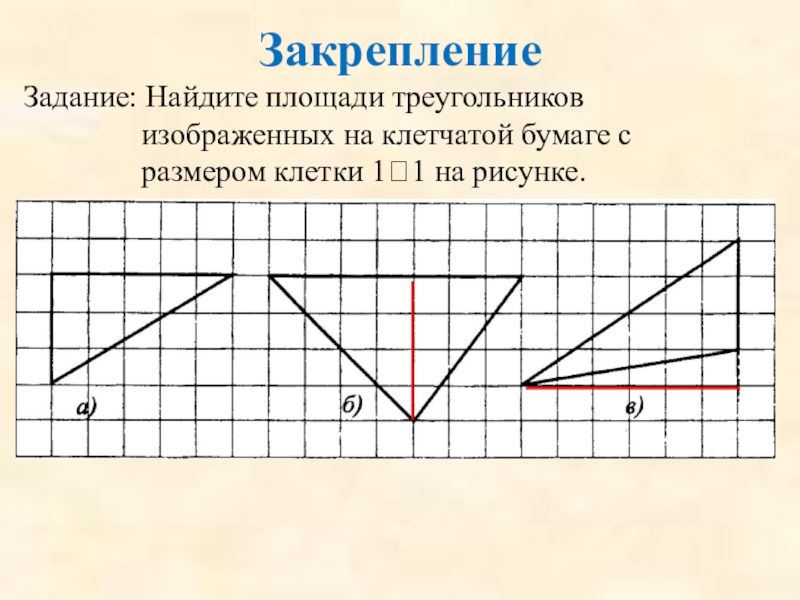
Задание: Найдите площади треугольников изображенных на клетчатой бумаге с размером клетки
Слайд 50Закрепление
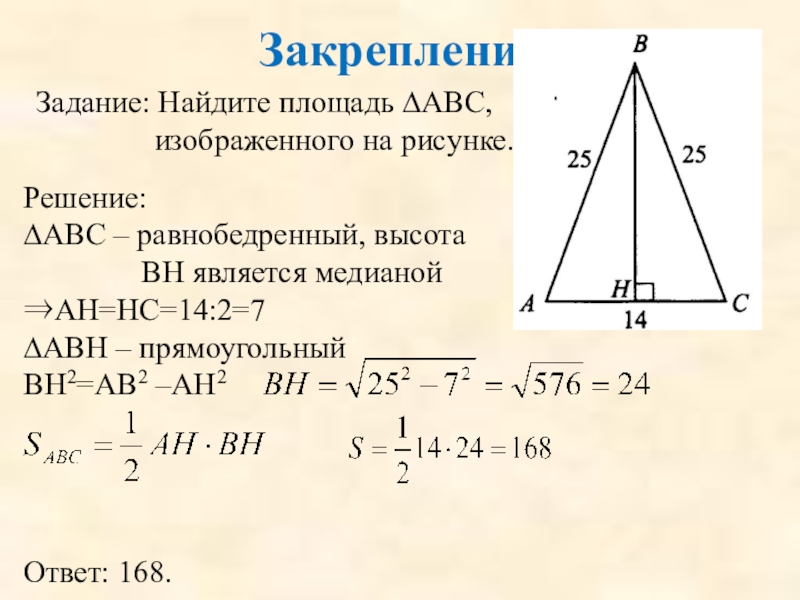
Задание: Найдите площадь ∆АВС, изображенного на рисунке.
Решение:
∆АВС – равнобедренный, высота
⇒АН=НС=14:2=7
∆АВН – прямоугольный
ВН2=АВ2 –АН2
Ответ: 168.
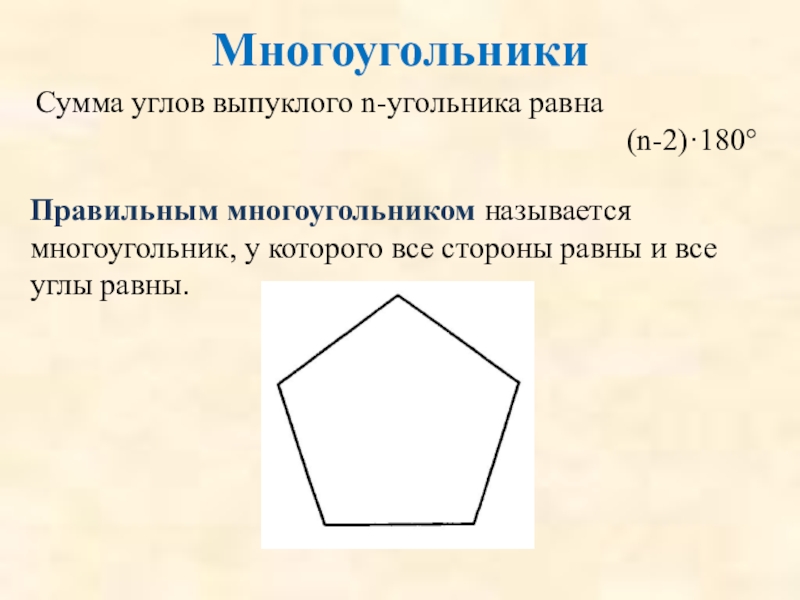
Слайд 51Многоугольники
Сумма углов выпуклого n-угольника равна
(n-2)·180°
Правильным многоугольником называется многоугольник, у которого
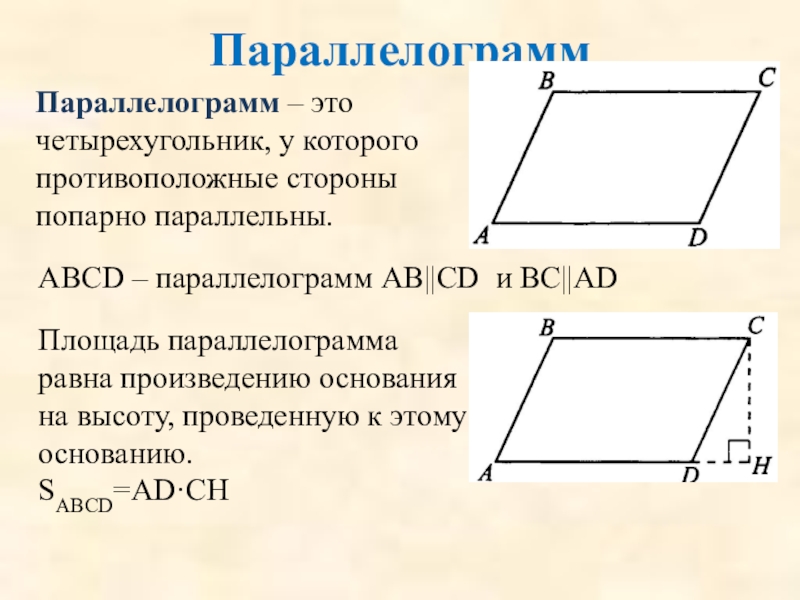
Слайд 52Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
АВСD
Площадь параллелограмма равна произведению основания на высоту, проведенную к этому основанию.
SABCD=АD·CH
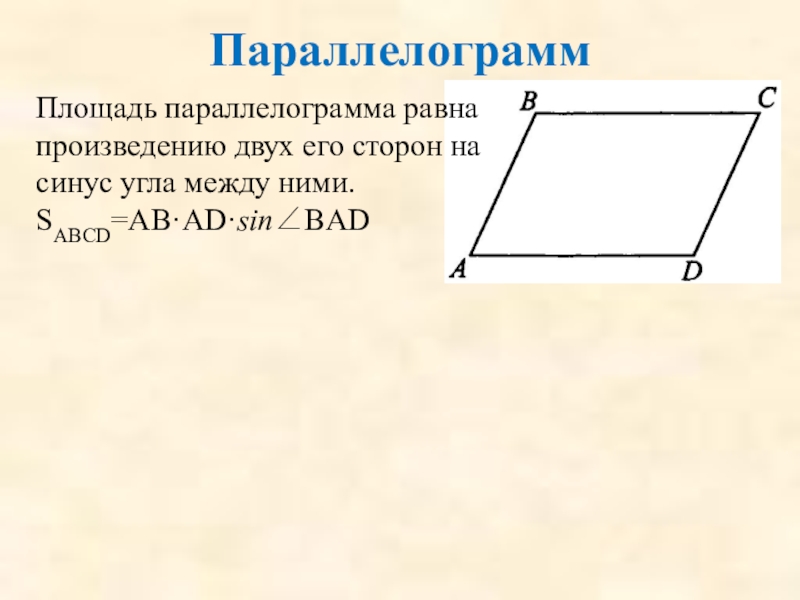
Слайд 53Параллелограмм
Площадь параллелограмма равна произведению двух его сторон на синус угла между
SABCD=АВ·АD·sin∠BAD
Слайд 54Свойства параллелограмма
Свойства:
Сумма углов параллелограмма равна 360°.
∠А+∠B+∠C+∠D=360°
2. В параллелограмме противоположные стороны равны.
АВ=CD
3. В параллелограмме противоположные углы равны.
∠А=∠С, ∠B=∠D
4. Диагонали параллелограмма точкой пересечения делятся пополам. AM=MC, BM=MD.
Слайд 55Признаки параллелограмма
Признаки:
Если в четырехугольнике две сторон равны и параллельны, то
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Слайд 56Закрепление
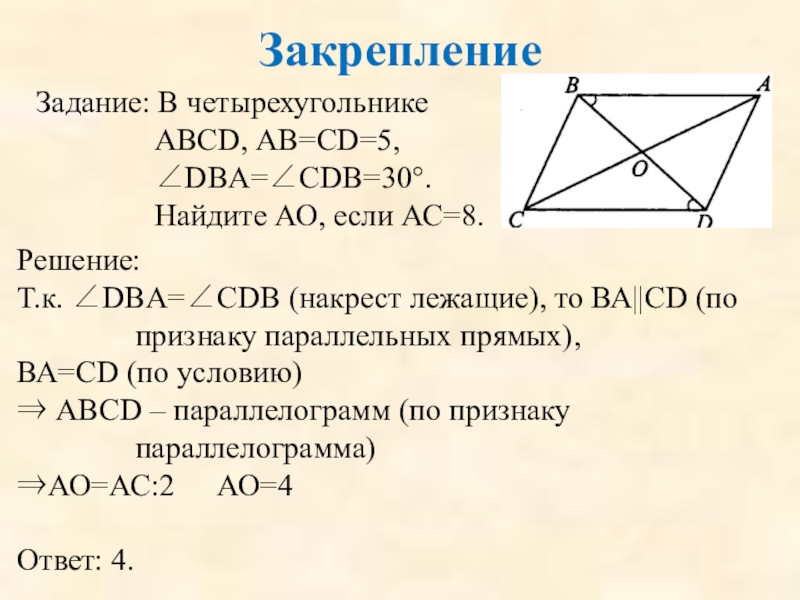
Задание: В четырехугольнике АВСD, АВ=СD=5, ∠DBA=∠CDB=30°. Найдите АО, если АС=8.
Решение:
Т.к. ∠DBA=∠CDB
ВА=СD (по условию)
⇒ АВСD – параллелограмм (по признаку параллелограмма)
⇒АО=АС:2 АО=4
Ответ: 4.
Слайд 57Трапеция
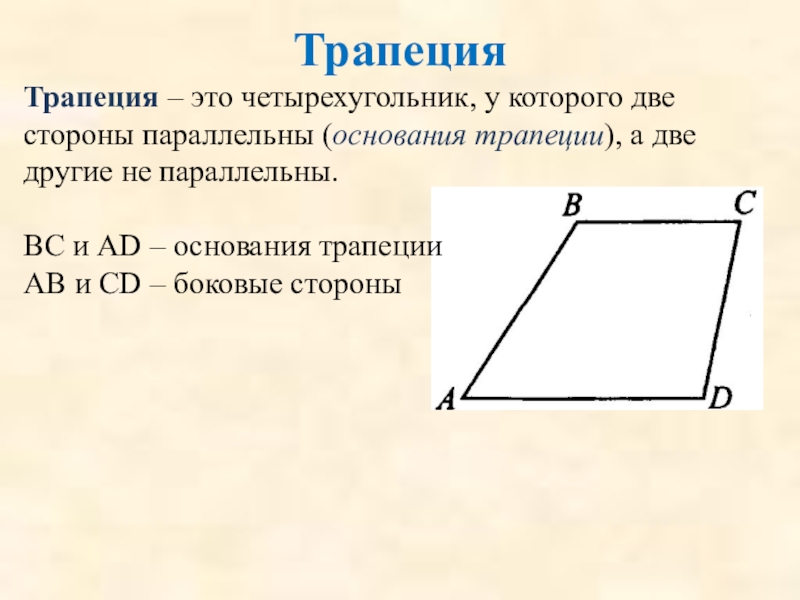
Трапеция – это четырехугольник, у которого две стороны параллельны (основания трапеции),
BC и AD – основания трапеции
АВ и CD – боковые стороны
Слайд 58Трапеция
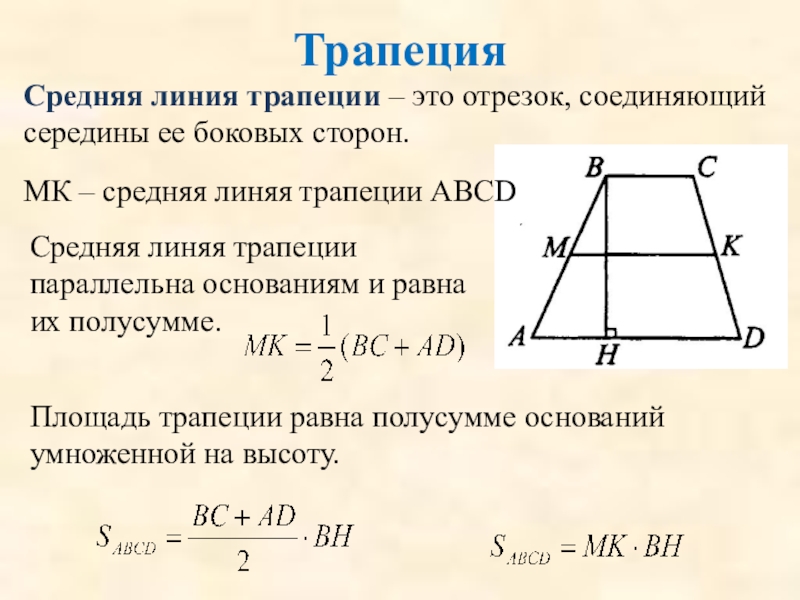
Площадь трапеции равна полусумме оснований умноженной на высоту.
Средняя линия трапеции –
МК – средняя линяя трапеции АВСD
Средняя линяя трапеции параллельна основаниям и равна их полусумме.
Слайд 59Трапеция
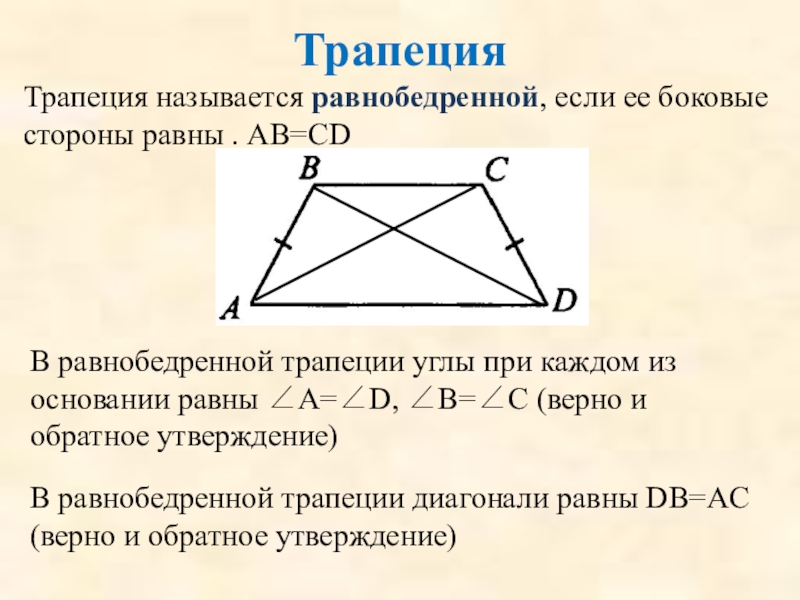
Трапеция называется равнобедренной, если ее боковые стороны равны . АВ=CD
В равнобедренной
В равнобедренной трапеции диагонали равны DВ=АC (верно и обратное утверждение)
Слайд 60Закрепление
Задание: Найдите площадь трапеции на рисунке.
Решение:
ВСЕF – параллелограмм (по признаку параллелограмма)
⇒FE=CB
∆АВF
AF2=АВ2 –BF2
⇒ED=4 AD=4+4+3=11
Ответ: 21.
Слайд 61Прямоугольник
Прямоугольник – это параллелограмм, у которого все углы прямые.
Если в
Площадь прямоугольника равна произведению его смежных сторон. SABCD=AB·AD
Диагонали любого прямоугольника равны.
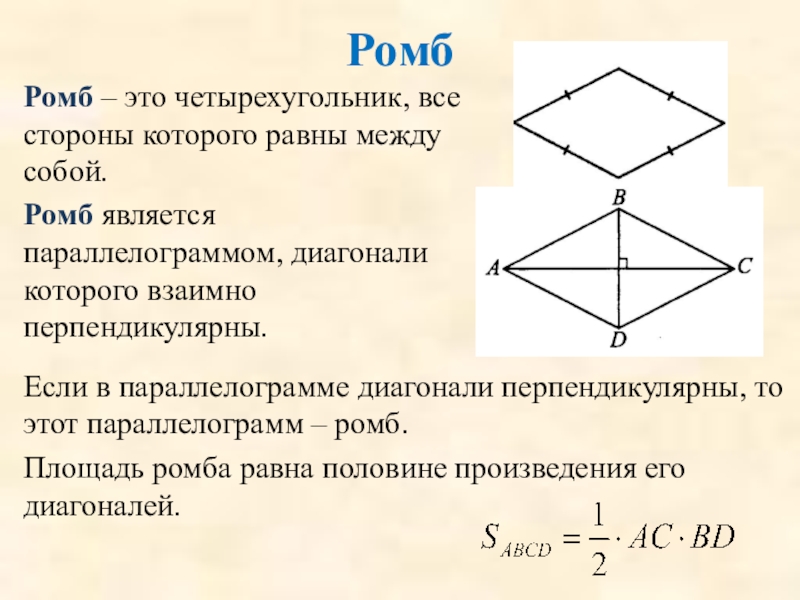
Слайд 62Ромб
Ромб – это четырехугольник, все стороны которого равны между собой.
Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм – ромб.
Площадь ромба равна половине произведения его диагоналей.
Ромб является параллелограммом, диагонали которого взаимно перпендикулярны.
Слайд 63Квадрат
Квадрат– это такой прямоугольник, у которого все стороны равны.
Квадрат также
Площадь квадрата равна квадрату его стороны. SABCD=AB2=а2
АС – диагональ квадрата.
Слайд 64Закрепление
Задание: Найдите площадь и высоту ромба ABCD, изображенного на рисунке.
Решение:
ВD=2·BO=2·6=12
AC=2·AO=2·8=16 (по
SABCD=АD·CH 96=10·CH CH=96:10=9,6
Ответ: 96; 9,6.
Слайд 65Закрепление
Задание: Укажите номера верных утверждений.
В равностороннем треугольнике все углы 90°.
Любой прямоугольник
В равнобедренной трапеции углы при основании равны.
Диагонали параллелограмма точкой пересечения делятся пополам.
Сумма двух соседних углов ромба может быть больше 180°.
Слайд 66Закрепление
Решение:
Неверно, т.к. в равностороннем треугольнике все углы 60°.
Неверно.
Верно, это свойство
Верно, это свойство параллелограмма.
Неверно, т.к. сумма двух соседних углов ромба равна180°.
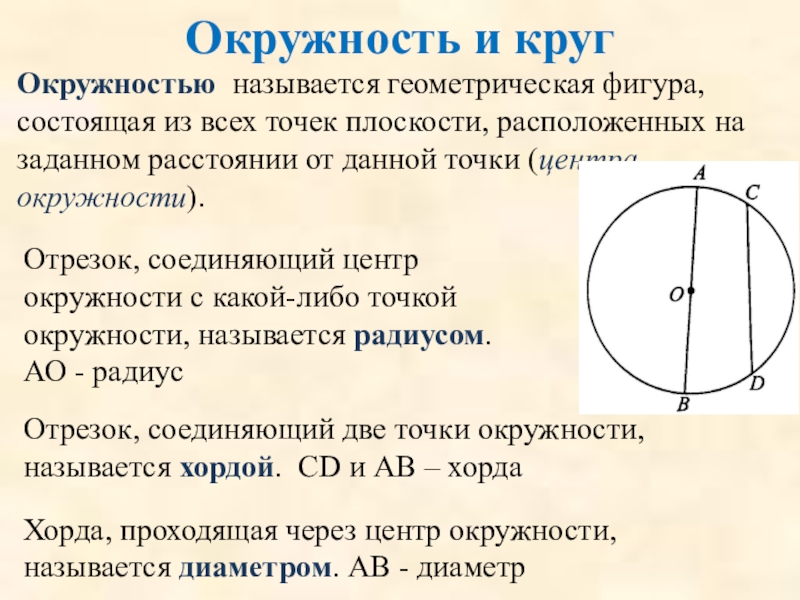
Слайд 67Окружность и круг
Окружностью называется геометрическая фигура, состоящая из всех точек плоскости,
Отрезок, соединяющий центр окружности с какой-либо точкой окружности, называется радиусом.
АО - радиус
Отрезок, соединяющий две точки окружности, называется хордой. СD и АВ – хорда
Хорда, проходящая через центр окружности, называется диаметром. АВ - диаметр
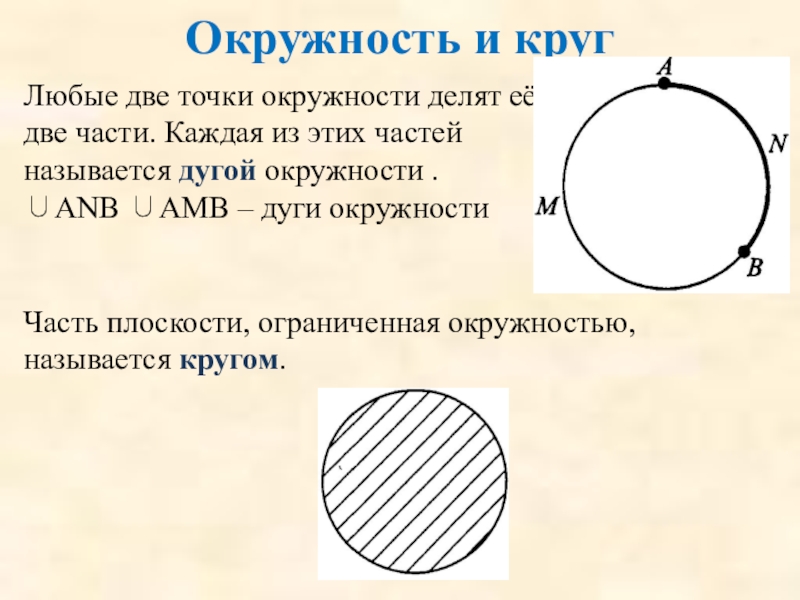
Слайд 68Окружность и круг
Любые две точки окружности делят её на две части.
∪АNB ∪AMB – дуги окружности
Часть плоскости, ограниченная окружностью, называется кругом.
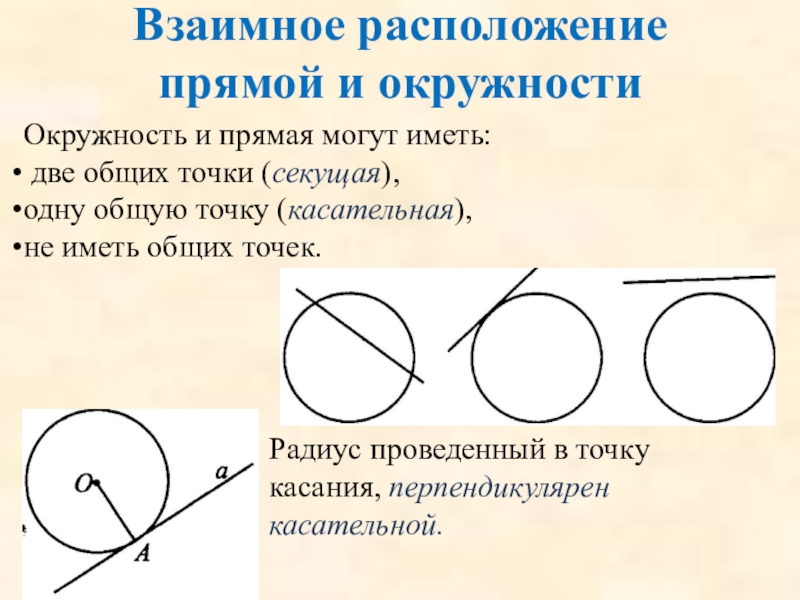
Слайд 69Взаимное расположение прямой и окружности
Окружность и прямая могут иметь:
две общих
одну общую точку (касательная),
не иметь общих точек.
Радиус проведенный в точку касания, перпендикулярен касательной.
Слайд 70Взаимное расположение двух окружностей
Две окружности могут иметь:
две общих точки (секущая),
одну общую точку (касательная),
не иметь общих точек.
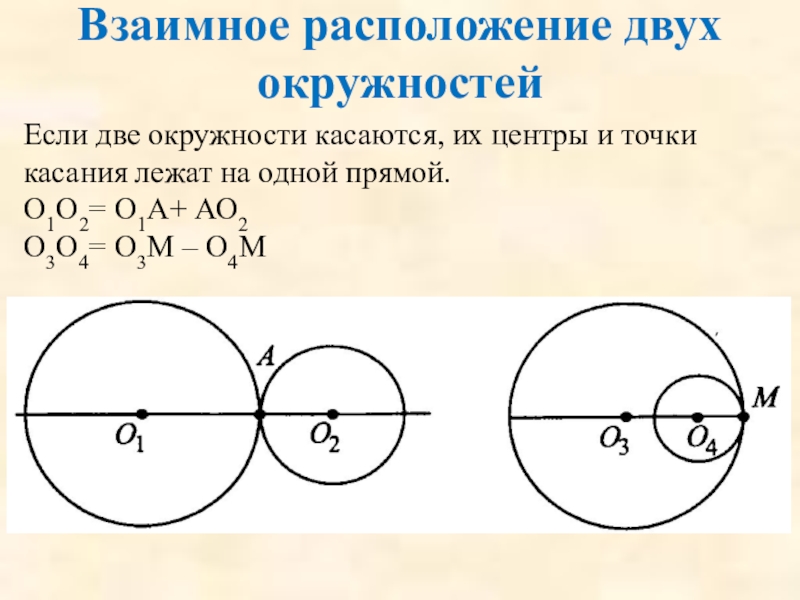
Слайд 71Взаимное расположение двух окружностей
Если две окружности касаются, их центры и точки
О1О2= О1А+ АО2
О3О4= О3М – О4М
Слайд 72Длина окружности и площадь круга
R – радиус окружности
D – диаметр окружности
Длина
L=2πR L=πd
Площадь круга, ограниченного данной окружностью
S=πR2
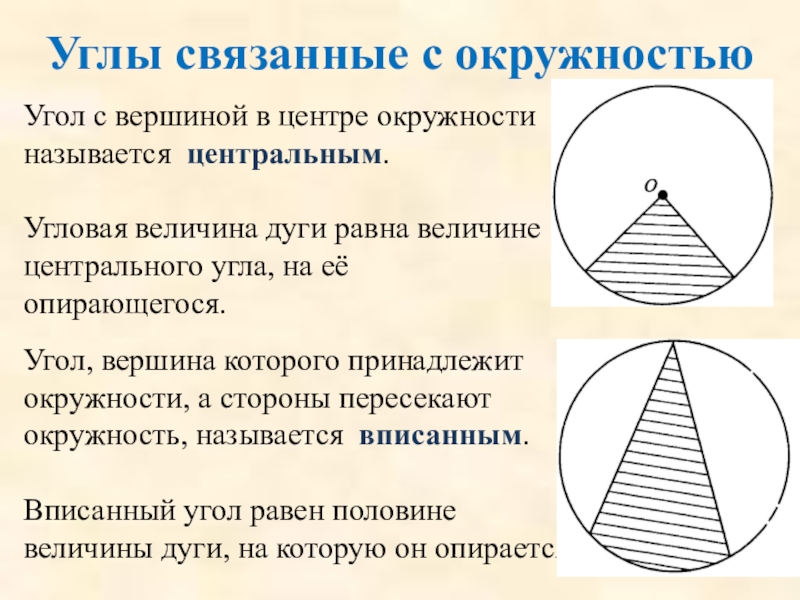
Слайд 73Углы связанные с окружностью
Угол с вершиной в центре окружности называется центральным.
Угловая величина дуги равна величине центрального угла, на её опирающегося.
Угол, вершина которого принадлежит окружности, а стороны пересекают окружность, называется вписанным.
Вписанный угол равен половине величины дуги, на которую он опирается.
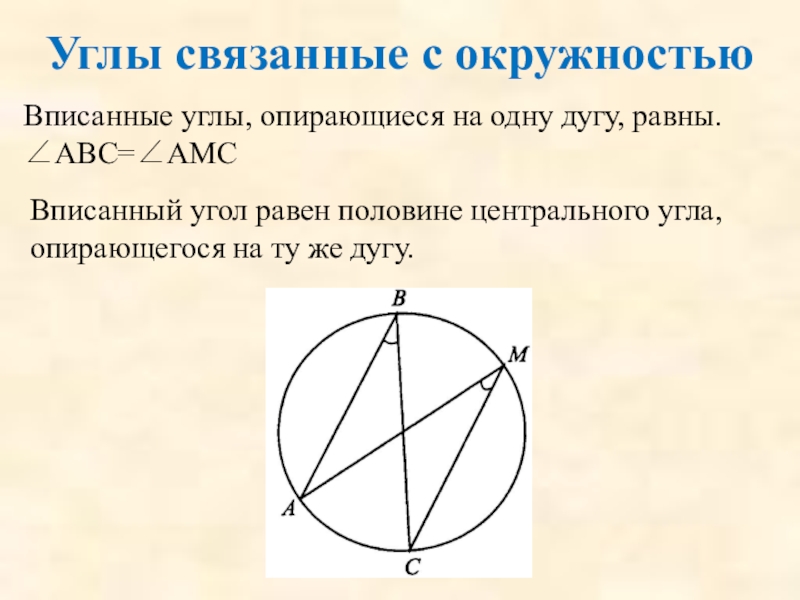
Слайд 74Углы связанные с окружностью
Вписанные углы, опирающиеся на одну дугу, равны.
∠АВС=∠АМС
Вписанный угол
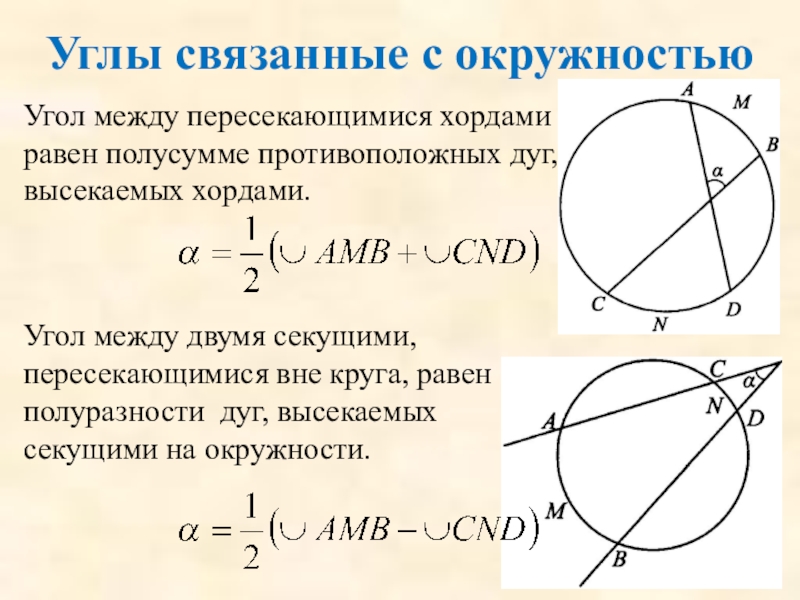
Слайд 75Углы связанные с окружностью
Угол между пересекающимися хордами равен полусумме противоположных дуг,
Угол между двумя секущими, пересекающимися вне круга, равен полуразности дуг, высекаемых секущими на окружности.
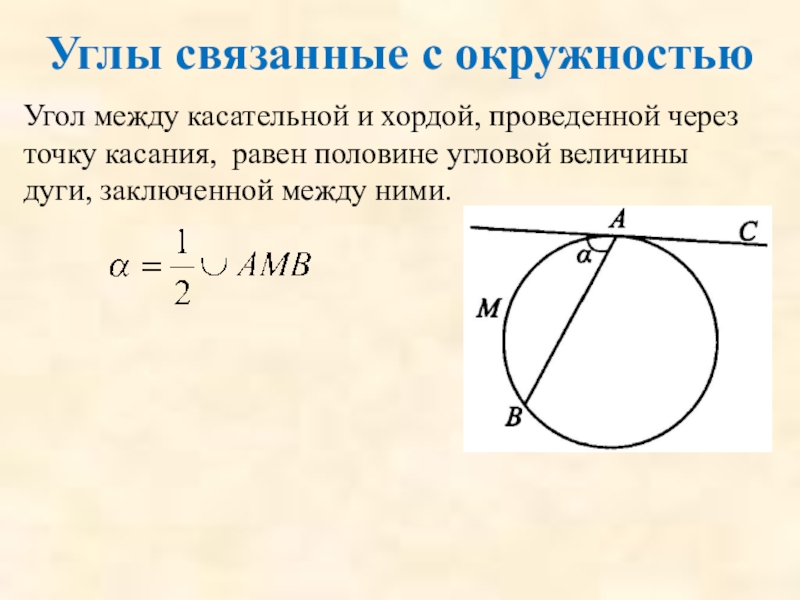
Слайд 76Углы связанные с окружностью
Угол между касательной и хордой, проведенной через точку
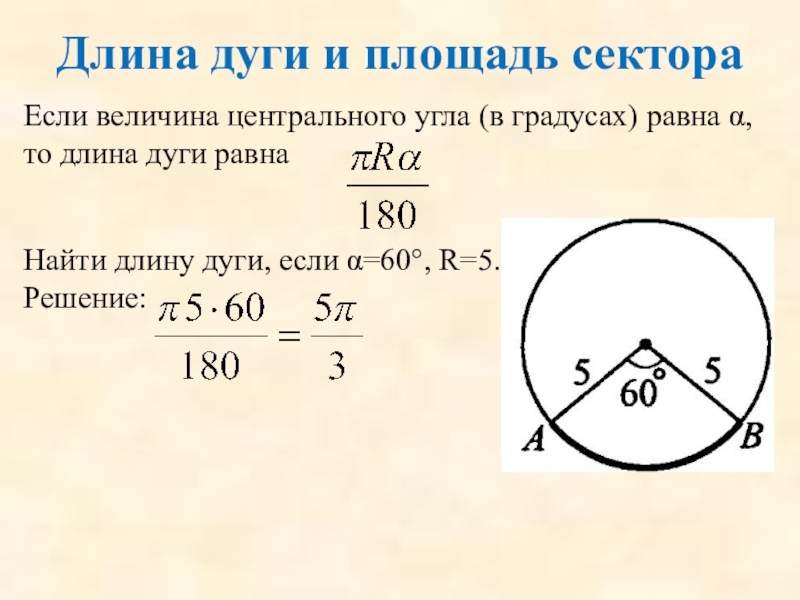
Слайд 77Длина дуги и площадь сектора
Если величина центрального угла (в градусах) равна
Найти длину дуги, если α=60°, R=5.
Решение:
Слайд 78Длина дуги и площадь сектора
Круговым сектором (или просто сектором) называется часть
Дуга, которая ограничивает сектор, называется дугой сектора.
Если величина дуги равна α (в градусах), то площадь сектора равна
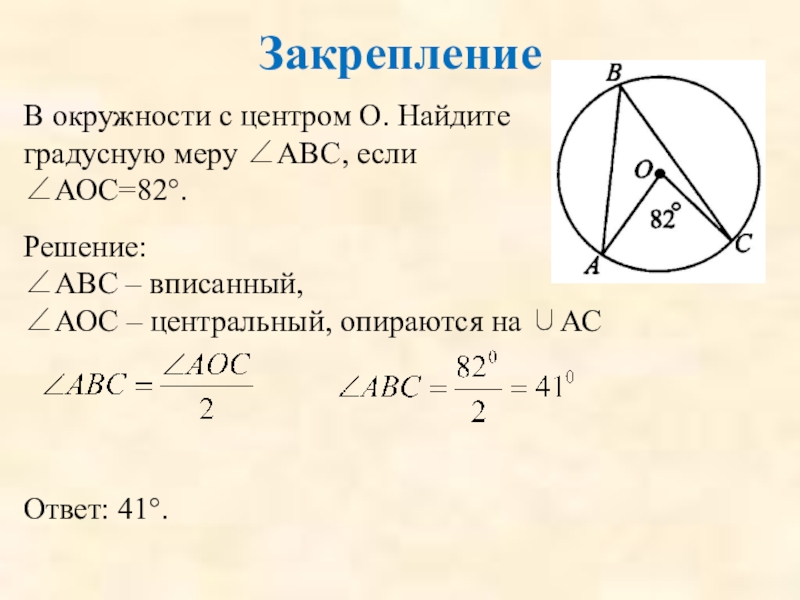
Слайд 79Закрепление
В окружности с центром О. Найдите градусную меру ∠АВС, если ∠АОС=82°.
Решение:
∠АВС – вписанный,
∠АОС – центральный, опираются на ∪АС
Ответ: 41°.
Слайд 80Треугольник и окружность
Вписанная окружность.
Биссектрисы треугольника пересекаются в одной точке, которая является
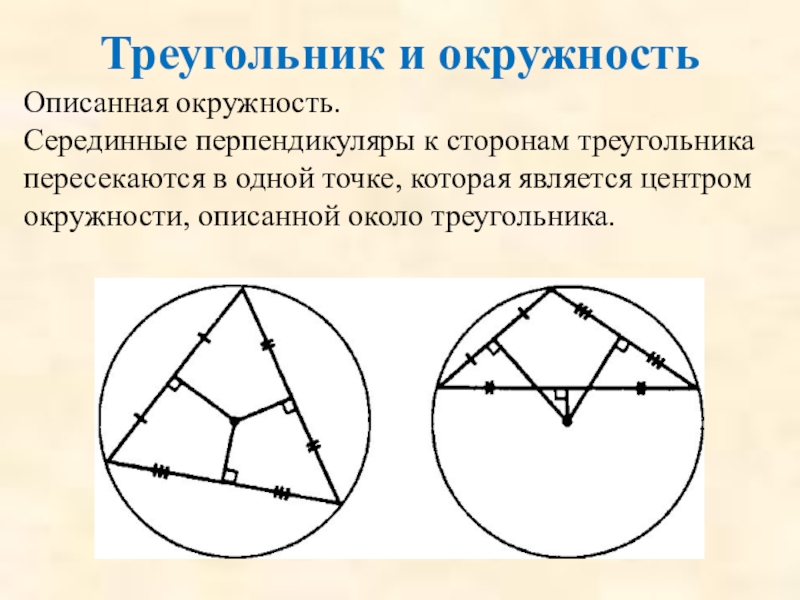
Слайд 81Треугольник и окружность
Описанная окружность.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной
Слайд 82Треугольник и окружность
Площадь треугольника равна произведению его полупериметра на радиус вписанной
Площадь треугольника равна произведению трех его сторон, деленному на учетверенный радиус описанной окружности.
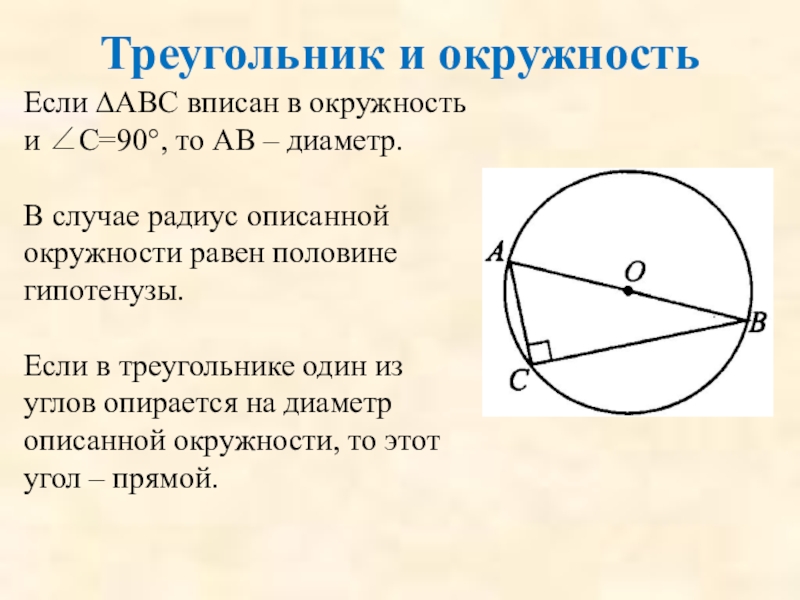
Слайд 83Треугольник и окружность
Если ∆АВС вписан в окружность и ∠С=90°, то АВ
В случае радиус описанной окружности равен половине гипотенузы.
Если в треугольнике один из углов опирается на диаметр описанной окружности, то этот угол – прямой.
Слайд 84Закрепление
На рисунке окружность с центром в точке О описана вокруг ∆АВС.
Решение:
∠АВС опирается на диаметр.
Значит, ∠АВС=90°, по теореме Пифагора
Ответ: 12,5.
Слайд 85Четырехугольник и окружность
В любом описанном четырехугольнике суммы противоположных сторон равны.
AD+BC=AB+CD
Если
Слайд 86Четырехугольник и окружность
В любом вписанном четырехугольнике сумма противоположных углов равна 180°.
∠BCD+∠BAD=∠CBA+∠CDA=180°
Если
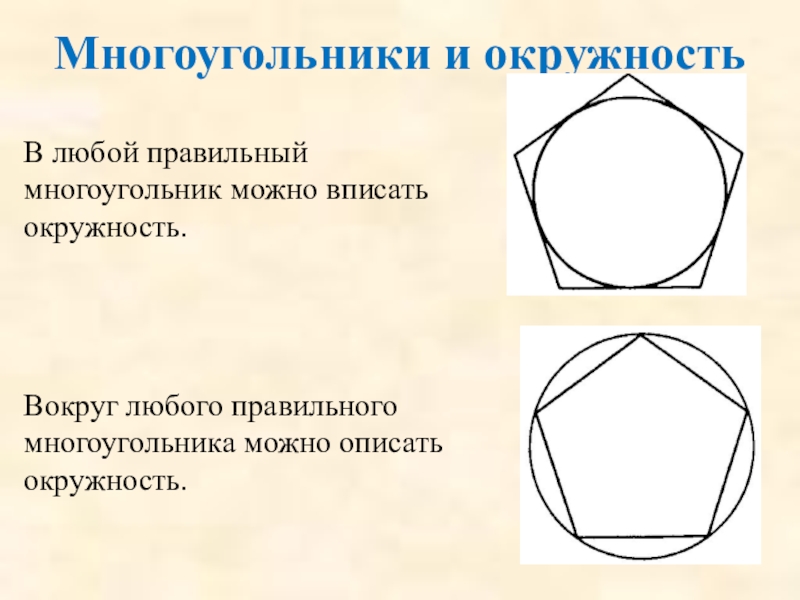
Слайд 87Многоугольники и окружность
В любой правильный многоугольник можно вписать окружность.
Вокруг любого правильного
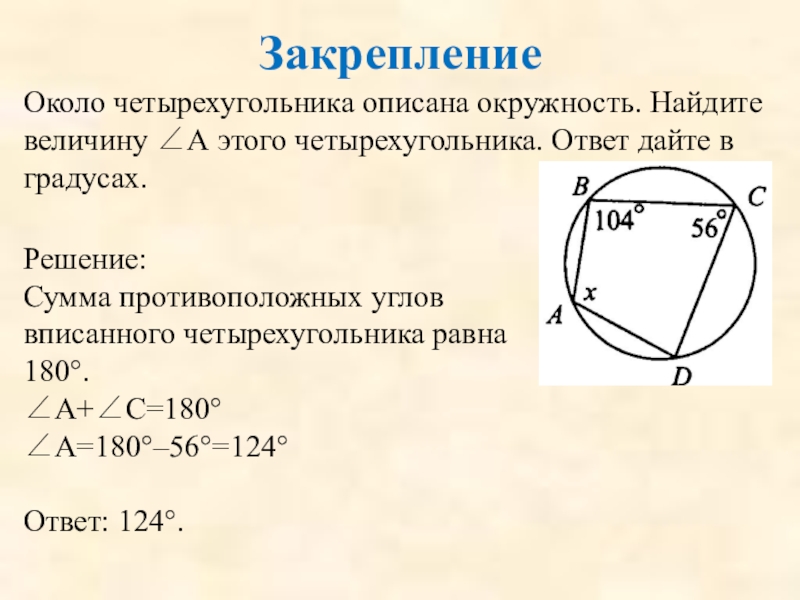
Слайд 88Закрепление
Около четырехугольника описана окружность. Найдите величину ∠А этого четырехугольника. Ответ дайте
Решение:
Сумма противоположных углов вписанного четырехугольника равна 180°.
∠А+∠С=180°
∠A=180°–56°=124°
Ответ: 124°.