- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для 10 класса на тему Призма
Содержание
- 1. Презентация для 10 класса на тему Призма
- 2. Призма (лат. Prisma - «нечто отпиленное») —
- 3. Призма, основанием которой является параллелограмм,
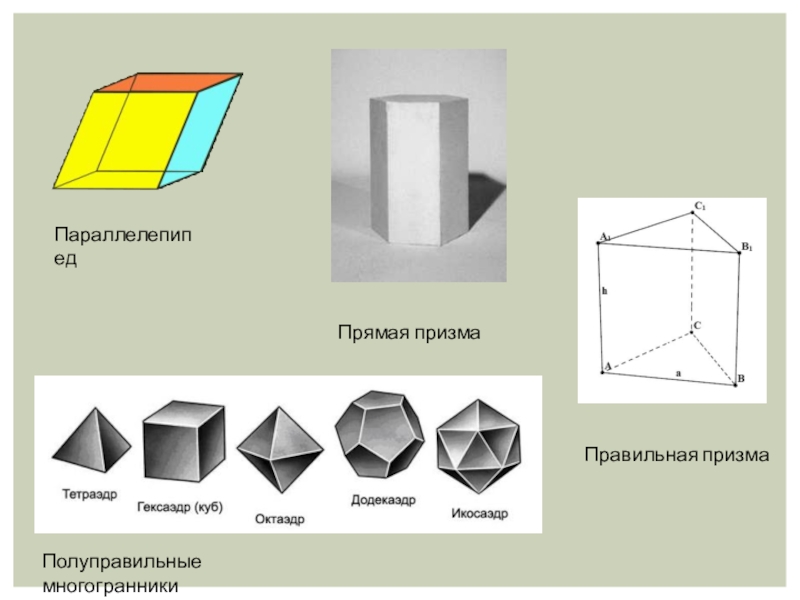
- 4. ПараллелепипедПрямая призма Правильная призма Полуправильные многогранники
- 5. Элементы призмыОснования - две грани, являющиеся конгруэнтными
- 6. Основания призмы - равные многоугольники. Боковые
- 7. ПризмаV – объем тела;Sб – площадь боковой
- 8. Основные формулыПризма, усечённая непараллельно основаниюl – длина
- 9. Прямоугольный параллелепипедa, b, c – рёбра;
- 10. Задачи из ЕГЭ.
- 11. Задания
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Спасибо за внимание.
Призма (лат. Prisma - «нечто отпиленное») — многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Или (равносильно) — это многогранник, в основаниях
Слайд 2Призма (лат. Prisma - «нечто отпиленное») — многогранник, две грани которого
являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Или (равносильно) — это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани — параллелограммы.
Призма – это…
Слайд 3 Призма, основанием которой является параллелограмм, называется параллелепипедом.
Прямая
призма - это призма, у которой боковые ребра перпендикулярны плоскости основания. Другие призмы называются наклонными.
Правильная призма - это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы - равные прямоугольники.
Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.
Правильная призма - это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы - равные прямоугольники.
Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.
Виды призм
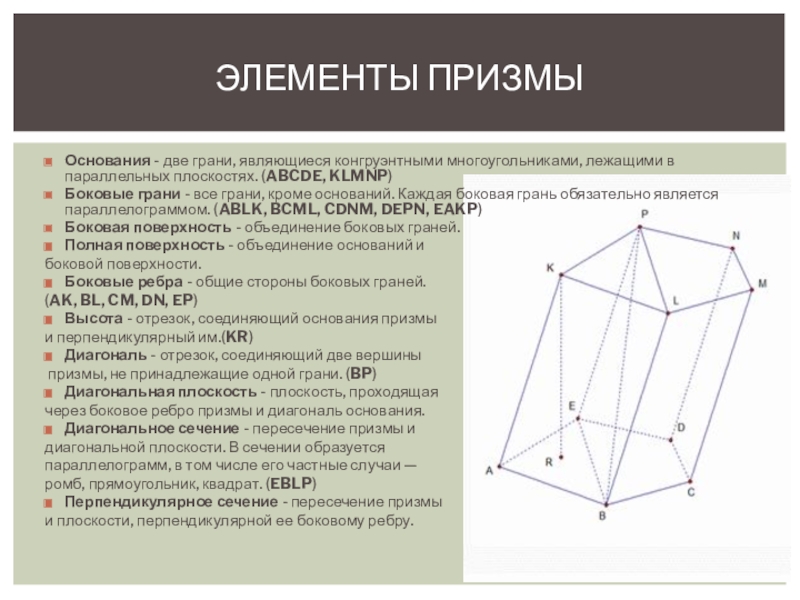
Слайд 5Элементы призмы
Основания - две грани, являющиеся конгруэнтными многоугольниками, лежащими в параллельных
плоскостях. (ABCDE, KLMNP)
Боковые грани - все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. (ABLK, BCML, CDNM, DEPN, EAKP)
Боковая поверхность - объединение боковых граней.
Полная поверхность - объединение оснований и
боковой поверхности.
Боковые ребра - общие стороны боковых граней.
(AK, BL, CM, DN, EP)
Высота - отрезок, соединяющий основания призмы
и перпендикулярный им.(KR)
Диагональ - отрезок, соединяющий две вершины
призмы, не принадлежащие одной грани. (BP)
Диагональная плоскость - плоскость, проходящая
через боковое ребро призмы и диагональ основания.
Диагональное сечение - пересечение призмы и
диагональной плоскости. В сечении образуется
параллелограмм, в том числе его частные случаи —
ромб, прямоугольник, квадрат. (EBLP)
Перпендикулярное сечение - пересечение призмы
и плоскости, перпендикулярной ее боковому ребру.
Боковые грани - все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. (ABLK, BCML, CDNM, DEPN, EAKP)
Боковая поверхность - объединение боковых граней.
Полная поверхность - объединение оснований и
боковой поверхности.
Боковые ребра - общие стороны боковых граней.
(AK, BL, CM, DN, EP)
Высота - отрезок, соединяющий основания призмы
и перпендикулярный им.(KR)
Диагональ - отрезок, соединяющий две вершины
призмы, не принадлежащие одной грани. (BP)
Диагональная плоскость - плоскость, проходящая
через боковое ребро призмы и диагональ основания.
Диагональное сечение - пересечение призмы и
диагональной плоскости. В сечении образуется
параллелограмм, в том числе его частные случаи —
ромб, прямоугольник, квадрат. (EBLP)
Перпендикулярное сечение - пересечение призмы
и плоскости, перпендикулярной ее боковому ребру.
Слайд 6 Основания призмы - равные многоугольники.
Боковые грани призмы - параллелограммы.
Боковые ребра призмы параллельны и равны.
Объём призмы равен произведению её высоты на площадь основания. (V = h*S)
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
(Sп.п = Sбок.+2Sосн.)
Площадь боковой поверхности произвольной призмы S = P*L, где P — периметр перпендикулярного сечения, L — длина бокового ребра.
Площадь боковой поверхности правильной призмы S = P* h, где P — периметр основания призмы, , h — высота призмы.
Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы.
Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах.
Перпендикулярное сечение перпендикулярно ко всем боковым граням.
Объём призмы равен произведению её высоты на площадь основания. (V = h*S)
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
(Sп.п = Sбок.+2Sосн.)
Площадь боковой поверхности произвольной призмы S = P*L, где P — периметр перпендикулярного сечения, L — длина бокового ребра.
Площадь боковой поверхности правильной призмы S = P* h, где P — периметр основания призмы, , h — высота призмы.
Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы.
Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах.
Перпендикулярное сечение перпендикулярно ко всем боковым граням.
Свойства призмы
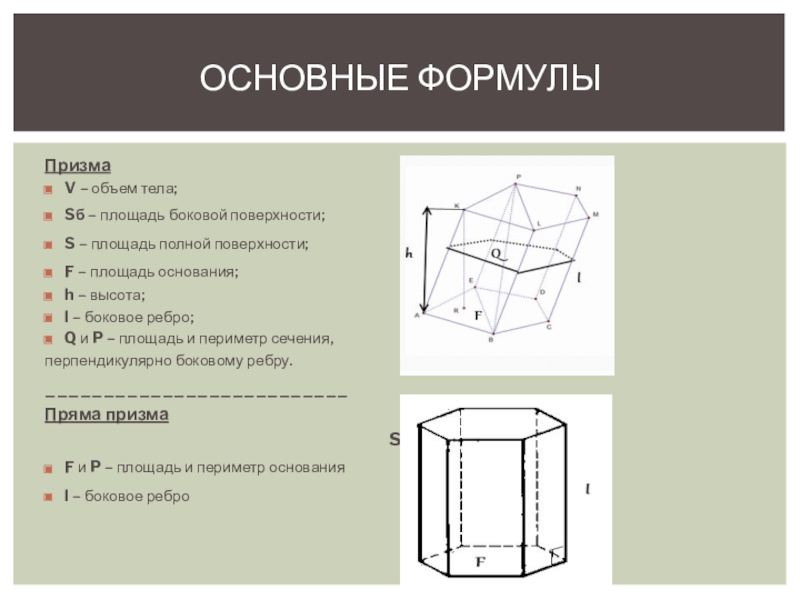
Слайд 7Призма
V – объем тела;
Sб – площадь боковой поверхности;
V =F*h=Q*l
S – площадь полной поверхности; Sб = P*l
F – площадь основания; S = P*l + 2F
h – высота;
l – боковое ребро;
Q и P – площадь и периметр сечения,
перпендикулярно боковому ребру.
__________________________ __________
Пряма призма
S = P*l + 2F
F и P – площадь и периметр основания V = F*l
l – боковое ребро Sб = P*l
S – площадь полной поверхности; Sб = P*l
F – площадь основания; S = P*l + 2F
h – высота;
l – боковое ребро;
Q и P – площадь и периметр сечения,
перпендикулярно боковому ребру.
__________________________ __________
Пряма призма
S = P*l + 2F
F и P – площадь и периметр основания V = F*l
l – боковое ребро Sб = P*l
Основные формулы
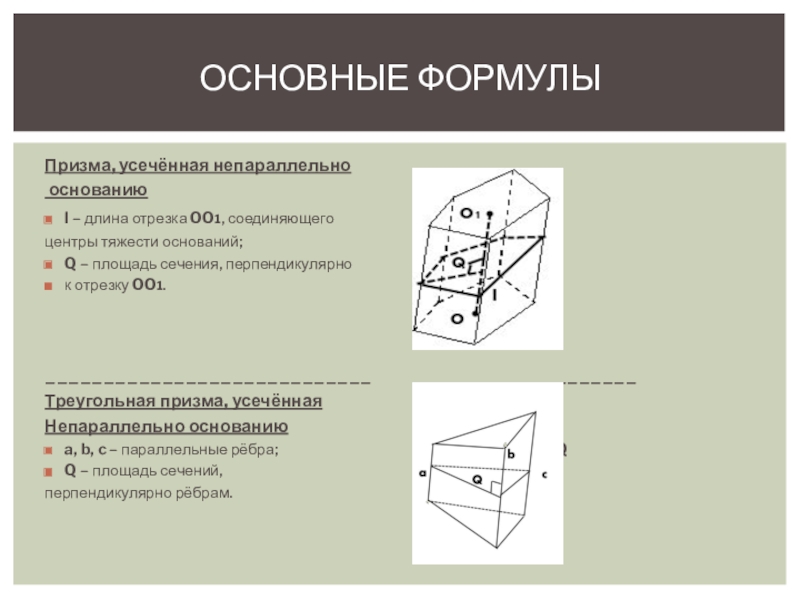
Слайд 8Основные формулы
Призма, усечённая непараллельно
основанию
l – длина отрезка OO1, соединяющего
V = Q*l
центры тяжести оснований;
Q – площадь сечения, перпендикулярно
к отрезку OO1.
____________________________ _____________
Треугольная призма, усечённая
Непараллельно основанию
a, b, c – параллельные рёбра; V = 1\3*(a+b+c)*Q
Q – площадь сечений,
перпендикулярно рёбрам.
центры тяжести оснований;
Q – площадь сечения, перпендикулярно
к отрезку OO1.
____________________________ _____________
Треугольная призма, усечённая
Непараллельно основанию
a, b, c – параллельные рёбра; V = 1\3*(a+b+c)*Q
Q – площадь сечений,
перпендикулярно рёбрам.
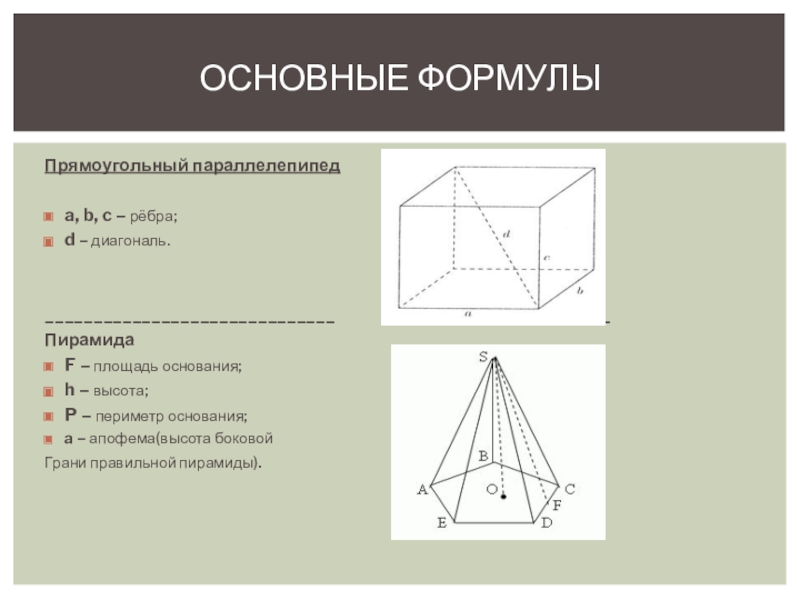
Слайд 9Прямоугольный параллелепипед
a, b, c – рёбра;
V = a*b*c
d – диагональ. S=2(ab+bc+ac)
d²=a²+b²+c²
______________________________ _____________
Пирамида
F – площадь основания; V = 1\3*F*h
h – высота; Sб = 1\2*p*a
P – периметр основания;
a – апофема(высота боковой
Грани правильной пирамиды).
d – диагональ. S=2(ab+bc+ac)
d²=a²+b²+c²
______________________________ _____________
Пирамида
F – площадь основания; V = 1\3*F*h
h – высота; Sб = 1\2*p*a
P – периметр основания;
a – апофема(высота боковой
Грани правильной пирамиды).
Основные формулы