- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Четырехугольники презентация содержит теоретический и практический материал
Содержание
- 1. Презентация Четырехугольники презентация содержит теоретический и практический материал
- 2. Слайд 2
- 3. Параллелограмм Опр. Четырехугольник, у которого две стороны попарно параллельны, называется параллелограммомСвойство 1Свойство 2
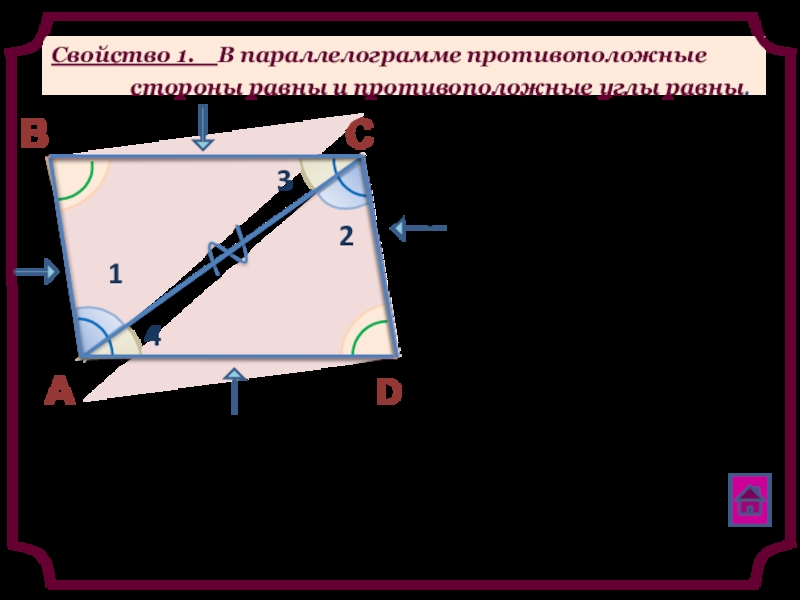
- 4. Свойство 1. В параллелограмме противоположные
- 5. АВ ⎢⎢ СD, ВD, AC – секущие
- 6. Прямоугольник Прямоугольник – это параллелограмм, у которого все углы прямые. Свойства прямоугольника
- 7. Свойства прямоугольника1. Противоположные стороны равны (AB=CD; BC=AD)2.
- 8. Ромб ОпределениеПараллелограмм, у которого все стороны равны. Свойства ромба
- 9. Свойства ромба СвойстваСвойство диагоналей параллелограмма:АС∩BD=O, AO=OC,
- 10. Квадрат ОпределениеПрямоугольник, у которого все стороны равны. Свойства квадрата
- 11. Квадрат СвойстваСвойство диагоналей параллелограмма:АС∩BD=O, AO=OC, BO=ODСвойство
Слайд 3Параллелограмм
Опр. Четырехугольник, у которого две стороны попарно параллельны, называется параллелограммом
Свойство
Свойство 2
Слайд 4Свойство 1. В параллелограмме противоположные
А
С
В
D
1
2
3
4
Дано: ABCD - параллелограмм
Доказать: 1) АВ = СD, BC = AD;
2) A = C, B = D
Доказательство: рассмотрим ∆ ABCи ∆ADC,
AC - общая,
1 = 2 и 3 = 4 (как накрест лежащие углы)
∆ АВС = ∆ ADC (по 2-му признаку равенства треугольников)
Следовательно: АВ = СD, BC = AD;
1 + 4= 2 + 3 , т.е. A = C, B = D.
Слайд 5АВ ⎢⎢ СD, ВD, AC – секущие
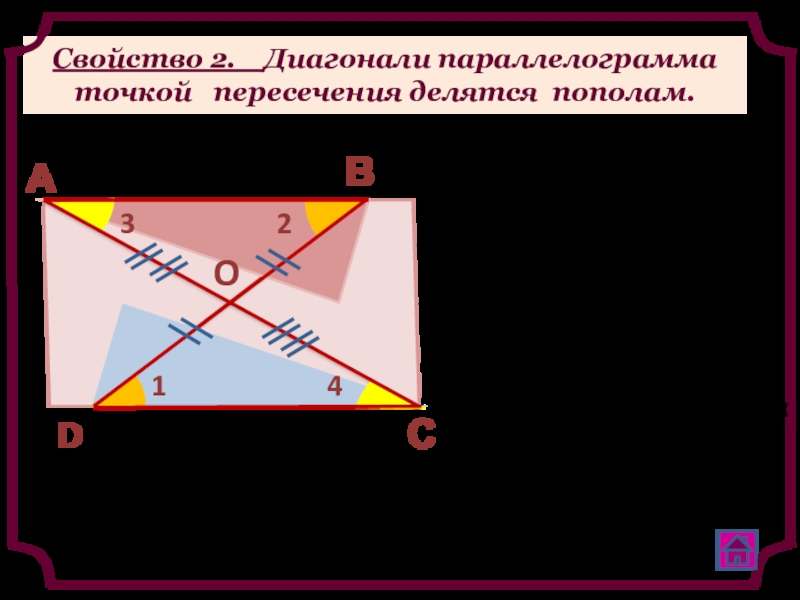
Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.
В
А
С
D
1
2
3
4
Дано: АВСD - параллелограмм
ВD AC = O
Доказать: ВО = ОD, АО = ОС
Доказательство:
рассмотрим ∆ АОВ и ∆СОD,
Следовательно: АО = ОС, ВО = ОD
∆ АОВ = ∆СОD (по 2-му признаку равенства треугольников)
O
АВ = СD (противоположные стороны параллелограмма,
Слайд 6
Прямоугольник
Прямоугольник – это
параллелограмм, у
которого все углы
прямые.
Свойства
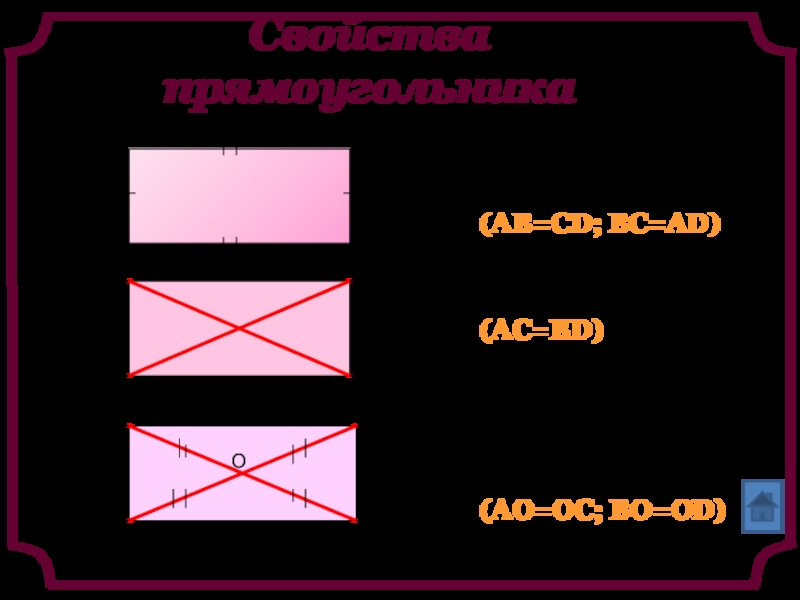
Слайд 7Свойства прямоугольника
1. Противоположные стороны равны (AB=CD; BC=AD)
2. Диагонали равны (AC=BD)
3. Диагонали
A
B
C
D
O
A
B
C
D
A
B
C
D
Слайд 9Свойства ромба
Свойства
Свойство диагоналей параллелограмма:
АС∩BD=O, AO=OC, BO=OD.
Свойство противолежащих сторон и
AB=CD, AD=BC.
Диагонали взаимно перпендикулярны и делят углы пополам.
Признаки
Если в четырехугольнике все стороны равны, то он ромб.
Если в параллелограмме диагонали делят его пополам, то он ромб.
Если в параллелограмме диагонали перпендикулярны, то он ромб.
Слайд 11Квадрат
Свойства
Свойство диагоналей параллелограмма:
АС∩BD=O, AO=OC, BO=OD
Свойство противолежащих сторон и углов:
AB=CD,
Диагонали взаимно перпендикулярны и делят углы пополам.
Признаки
Если диагонали четырехугольника пересекаются под прямым углом, то он квадрат.
Если в ромбе все углы равны, то он квадрат.
Если ромбе диагонали равны, то он квадрат.