- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Четыре замечательные точки треугольника
Содержание
- 1. Презентация Четыре замечательные точки треугольника
- 2. Слайд 2
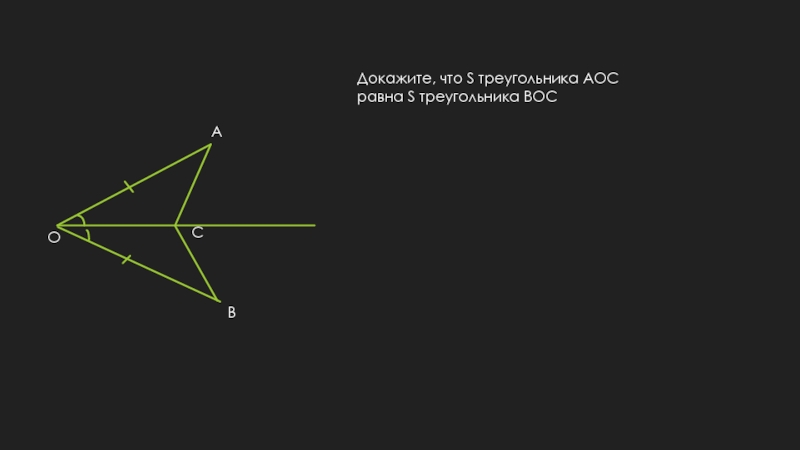
- 3. OACBДокажите, что S треугольника AOC равна S треугольника BOC
- 4. Свойства биссектрисы углаТеорема 1. Каждая точка биссектрисы
- 5. Теорема 3. Каждая точка серединного перпендикуляра к
- 6. Первая замечательная точка
- 7. Вторая замечательная точка треугольника — точка пересечения
- 8. Третья замечательная точка треугольника — точка пересечения
- 9. Четвёртая замечательная точка треугольника — точка пересечения
OACBДокажите, что S треугольника AOC равна S треугольника BOC
Слайд 1Четыре замечательные точки треугольника
Учитель математики ГБОУ СОШ№388
Кировского района Санкт-Петербурга
Садретдинова А. Л.
Слайд 4Свойства биссектрисы угла
Теорема 1. Каждая точка биссектрисы неразвёрнутого угла равноудалена от
его сторон.
Теорема 2. ( обратная).Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла.
Теорема 2. ( обратная).Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла.
Слайд 5Теорема 3. Каждая точка серединного перпендикуляра к отрезку равноудалена от его
концов.
Теорема 4. (обратная) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
Теорема 4. (обратная) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
Слайд 6
Первая замечательная точка треугольника — точка пересечения биссектрис
Теорема 5. Биссектрисы треугольника пересекаются
в одной точке.
Слайд 7Вторая замечательная точка треугольника — точка пересечения серединных перпендикуляров сторон треугольника
Теорема
6. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Слайд 8Третья замечательная точка треугольника — точка пересечения медиан
Теорема 7. Медианы треугольника
пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Точка пересечения медиан является центром тяжести треугольника.
Слайд 9Четвёртая замечательная точка треугольника — точка пересечения высот треугольника
Теорема 8. Высоты
треугольника или их продолжения пересекаются в одной точке.
Точку пересечения высот называется ортоцентром треугольника.