Клещеногова В.А.- учитель математики МБОУ «Мордовско- Полянская СОШ»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Правильные многоугольники (задачи на построение) (9 класс)
Содержание
- 1. Правильные многоугольники (задачи на построение) (9 класс)
- 2. Правильные многоугольники уже в глубокой древности считались
- 3. Практическая задача построения таких многоугольников с помощью
- 4. Долгое время математиков особенно занимал вопрос о
- 5. Рассмотрим задачи, в которых нужно найти способы
- 6. Вписанный n-угольникДокажите, что для построения правильного n-угольника,
- 7. Решение:Если все n сторон вписанного n-угольника стягивают
- 8. Сокращение числа сторон Дан правильный многоугольник, число
- 9. Решение:Пусть A1, A2, ..., Akm - последовательные вершины исходного
- 10. Удвоение числа сторон В окружность вписан правильный
- 11. Решение:Проведем к каждой стороне данного многоугольника свой
- 12. Заданный треугольник Постройте правильный треугольник со стороной, равной заданному отрезку.
- 13. Решение:Пусть АВ - заданный отрезок. Проведем две
- 14. Вписанный шестиугольник Впишите в данную окружность правильный шестиугольник.
- 15. Решение:Возьмем на данной окружности с центром О
- 16. Заданный шестиугольник Постройте правильный шестиугольник, со стороной, равной заданному отрезку.
- 17. Решение:Раствором циркуля, равным длине данного отрезка, проведем
- 18. Заданный квадрат Постройте квадрат со стороной, равной заданному отрезку.
- 19. Решение:Из концов данного отрезка АВ восставим перпендикуляры
- 20. Вписанный квадрат Впишите в данную окружность квадрат.
- 21. Решение:Через центр окружности проведем два взаимно перпендикулярных
- 22. Звезда Как построить пятиконечную звезду?
- 23. Решение:Нарисуем некоторую окружность, разделим ее на 5
- 24. Литература:«Примени математику»-И.Н.Сергеев, С.Н.Олехник, С.Б.Гашков, Москва «Наука», 1989г.Интернет- ресурсы.
Правильные многоугольники уже в глубокой древности считались символом красоты и совершенства. Это и понятно: ведь из всех многоугольников с заданным числом сторон наиболее приятен для глаза правильный многоугольник, у которого равны все стороны и равны все
Слайд 1Правильные многоугольники
(задачи на построение).
Слайд 2Правильные многоугольники уже в глубокой древности считались символом красоты и совершенства.
Это и понятно: ведь из всех многоугольников с заданным числом сторон наиболее приятен для глаза правильный многоугольник, у которого равны все стороны и равны все углы.
Слайд 3Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет
давнюю историю. Евклид в своем труде по геометрии приводит способы построения правильных треугольника, четырехугольника (квадрата), пятиугольника и пятнадцатиугольника, а также всех многоугольников, которые получаются из них удвоением числа сторон (не обязательно однократным). Следовательно, древние греки могли строить правильные многоугольники с числом сторон, равным
3, 4, 5, 6, 8, 10, 12, 15, 16, ...
3, 4, 5, 6, 8, 10, 12, 15, 16, ...
Слайд 4Долгое время математиков особенно занимал вопрос о построении правильного семиугольника. Лишь
в 1796 г. К. Ф. Гаусc доказал принципиальную невозможность этого построения с помощью только циркуля и линейки. Более того, им было доказано, что среди правильных многоугольников с нечетным числом сторон построить можно только такие, для которых число сторон является либо простым числом вида 22m + 1, m = 0, 1, 2, ... (которых в настоящее время известно всего пять: 3, 5, 17, 257 и 65 537), либо произведением нескольких таких различных чисел. Таким образом, начатый выше список нельзя дополнить числами 7, 9, 11, 13, 14, а можно лишь продолжить следующим образом:
17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, ...
17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, ...
Слайд 5Рассмотрим задачи, в которых нужно найти способы построения правильных многоугольников, вписанных
в данную окружность или имеющих заданную сторону. Не менее важное практическое значение имеют методы приближенного построения в тех случаях, когда точное построение циркулем и линейкой неосуществимо.
Слайд 6Вписанный n-угольник
Докажите, что для построения правильного n-угольника, вписанного в данную окружность,
достаточно разделить эту окружность на n равных частей и полученные точки деления последовательно соединить кордами. Как можно приближенно разделить окружность на заданное число равных дуг?
Слайд 7Решение:
Если все n сторон вписанного n-угольника стягивают равные дуги окружности, то
сами стороны равны между собой. Кроме того, в этом случае каждый из углов между соседними сторонами n-угольника является вписанным и опирается на дугу, составленную из n-2 упомянутых одинаковых дуг. Следовательно, все эти углы также равны между собой. Таким образом, задача построения вписанного правильного n-угольника сведена к делению окружности на n равных дуг.
Слайд 8Сокращение числа сторон
Дан правильный многоугольник, число сторон которого представляет собой
произведение натуральных чисел k и m, где m>2.Как построить правильный m-угольник?
Слайд 9Решение:
Пусть A1, A2, ..., Akm - последовательные вершины исходного многоугольника. Тогда многоугольник с
вершинами A1, A2, ..., Akm будет правильным, поскольку эти вершины лежат на одной окружности (описанной около исходного многоугольника) и делят ее на равные дуги.
Слайд 10Удвоение числа сторон
В окружность вписан правильный многоугольник. Постройте правильный многоугольник, у
которого число сторон вдвое больше, чем у исходного.
Слайд 11Решение:
Проведем к каждой стороне данного многоугольника свой серединный перпендикуляр до его
пересечения о дугой окружности, стягиваемой этой стороной. Так как полученные точки пересечения разделят каждую из дуг на две равные части, то эти точки вместе с вершинами исходного многоугольника образуют вершины требуемого многоугольника.
Слайд 12Заданный треугольник
Постройте правильный треугольник со стороной, равной заданному отрезку.
Слайд 13Решение:
Пусть АВ - заданный отрезок. Проведем две дуги окружностей с центрами
в точках A и B и радиусом AВ до пересечения их в точке С. Соединив точки A и B с точкой С, получим требуемый правильный треугольник ABC.
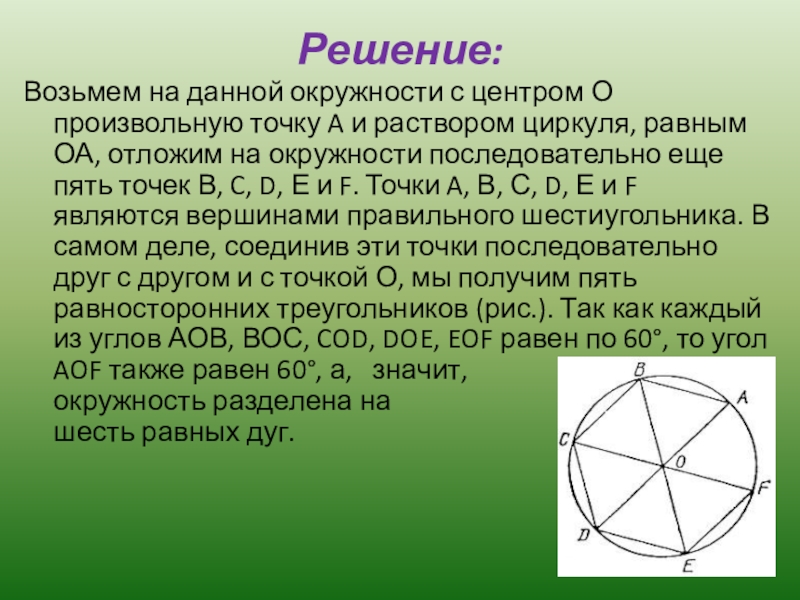
Слайд 15Решение:
Возьмем на данной окружности с центром О произвольную точку A и
раствором циркуля, равным ОА, отложим на окружности последовательно еще пять точек В, C, D, Е и F. Точки A, В, С, D, Е и F являются вершинами правильного шестиугольника. В самом деле, соединив эти точки последовательно друг с другом и с точкой О, мы получим пять равносторонних треугольников (рис.). Так как каждый из углов АОВ, ВОС, COD, DOE, EOF равен по 60°, то угол AOF также равен 60°, а, значит, окружность разделена на шесть равных дуг.
Слайд 16Заданный шестиугольник
Постройте правильный шестиугольник, со стороной, равной заданному отрезку.
Слайд 17Решение:
Раствором циркуля, равным длине данного отрезка, проведем окружность. Вписав в эту
окружность шестиугольник способом, предложенным в решении предыдущей задачи, мы получим правильный шестиугольник с заданной стороной.
Слайд 19Решение:
Из концов данного отрезка АВ восставим перпендикуляры AM и BN по
одну сторону от отрезка АВ (рис.) и отложим на них соответственно отрезки AD и ВС, равные отрезку АВ, Соединив точки С и D, получим квадрат ADCB. В самом деле, четырехугольник ADCB является параллелограммом (ибо его стороны AD и ВС равны и параллельны), ромбом (ибо АВ = ВС) и прямоугольником (ибо ∠ ABC = 90°), а значит, квадратом.
Слайд 21Решение:
Через центр окружности проведем два взаимно перпендикулярных диаметра АС и BD
и их концы последовательно соединим хордами. Получим вписанный квадрат ABCD. Действительно, дуги АВ, ВС, CD и AD равны между собой, поскольку на них опираются равные центральные углы в 90° каждый.
Слайд 23Решение:
Нарисуем некоторую окружность, разделим ее на 5 равных частей (угол=72град) и
соединим точки деления через одну хордами друг с другом, как указано на рис.