- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Правильные многогранники.Урок геометрии в 10 классе.
Содержание
- 1. Правильные многогранники.Урок геометрии в 10 классе.
- 2. Правильных многогранников вызывающе мало, но этот весьма
- 3. Осевая симметрияДве точки А и А1 называются
- 4. Центральная симметрияДве точки А и А1 называются
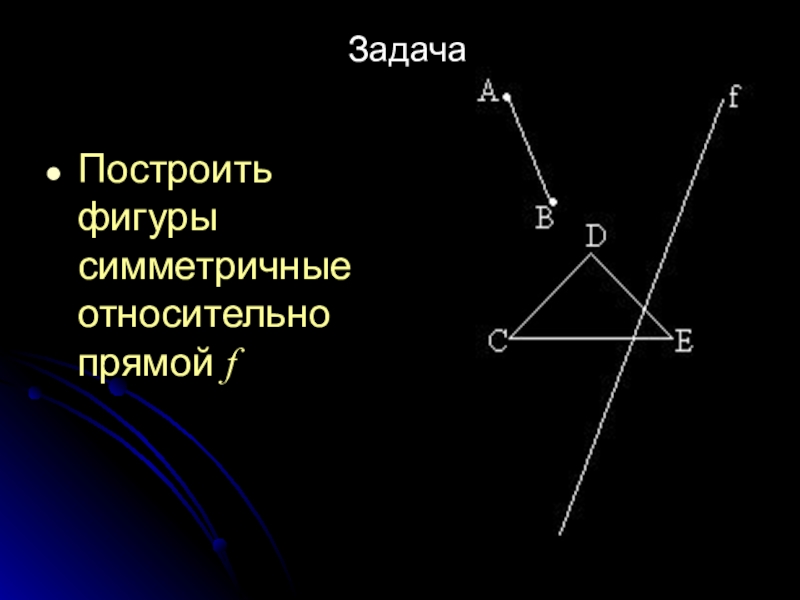
- 5. Задача Построить фигуры симметричные относительно прямой f
- 6. Симметрия относительно плоскостиТочки А и А1 называются
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Определение правильного многогранника Выпуклый многогранник называется правильным,
- 12. Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники.
- 13. Правильный ТЕТРАЭДРСоставлен из четырёх равносторонних треугольников. Каждая
- 14. Правильный ОКТАЭДРСоставлен из восьми равносторонних треугольников. Каждая
- 15. Правильный икосаэдрСоставлен из двадцати равносторонних треугольников. Каждая
- 16. Куб (гексаэдр) Составлен из шести квадратов. Каждая
- 17. Правильный додекаэдрСоставлен из двенадцати правильных пятиугольников. Каждая
- 18. Названия многогранников пришли из Древней Грециив
- 19. Правильные многогранники в философской картине мира ПЛАТОНА огоньвода
- 20. «Космический кубок» КеплераМодель Солнечной системы И. Кеплера
- 21. Икосаэдро-додекаэдровая структура Земли
- 22. Таблица № 1
- 23. Таблица № 1
- 24. Таблица № 2
- 25. Таблица № 2
- 26. Формула ЭйлераСумма числа граней и вершин любого
- 27. Правильные многогранники и природа
- 28. Задача: Определите количество граней, вершин и
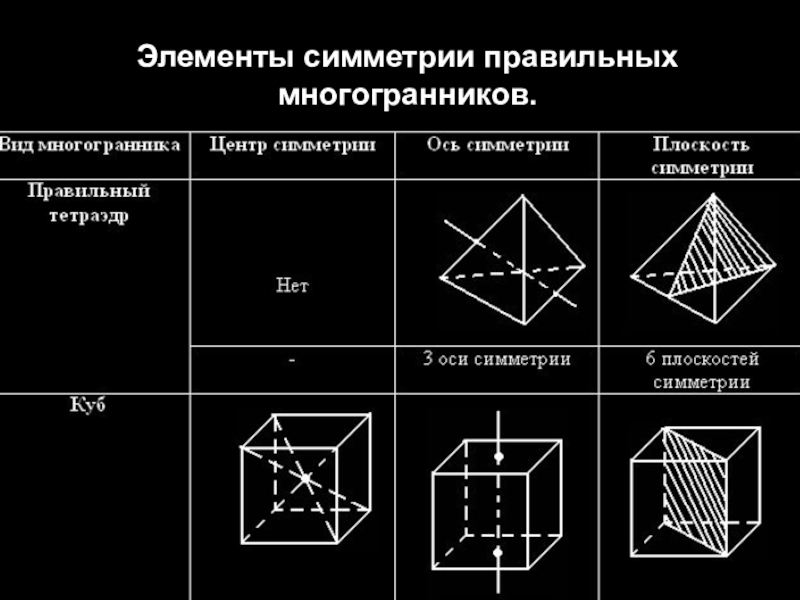
- 29. Элементы симметрии правильных многогранников.
- 30. Правильный октаэдр, правильный икосаэдр, правильный додекаэдр имеют центр симметрии и несколько осей и плоскостей симметрии.
Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л.Кэролл
Слайд 1
Симметрия в пространстве
Понятие правильного многогранника
Элементы симметрии правильных многогранников
Слайд 2 Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд
сумел пробраться в самые глубины различных наук.
Л.Кэролл
Л.Кэролл
Слайд 3Осевая симметрия
Две точки А и А1 называются симметричными относительно прямой а
(оси симметрии), если прямая а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку.
Слайд 4Центральная симметрия
Две точки А и А1 называются симметричными относительно точки О,
если О – середина отрезка АА1. Точка О считается симметричной самой себе.
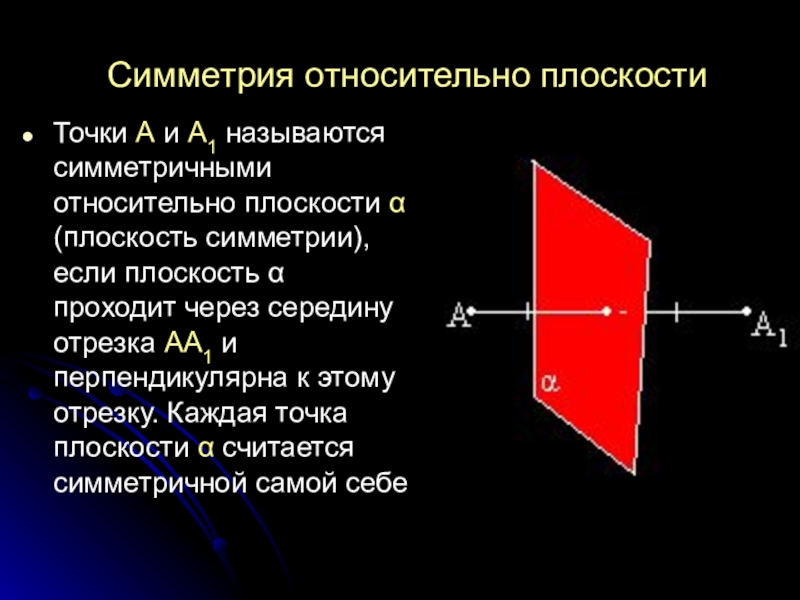
Слайд 6Симметрия относительно плоскости
Точки А и А1 называются симметричными относительно плоскости α(плоскость
симметрии), если плоскость α проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка плоскости α считается симметричной самой себе
Слайд 11Определение правильного многогранника
Выпуклый многогранник называется правильным, если его грани являются
правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.
Слайд 12
Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и
вообще n-угольники.
Слайд 13Правильный ТЕТРАЭДР
Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной
трёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180º
Слайд 14Правильный ОКТАЭДР
Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной
четырёх треугольников. Следовательно, сумма плоских углов при каждой вершине 240º
Слайд 15Правильный икосаэдр
Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной
пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300º
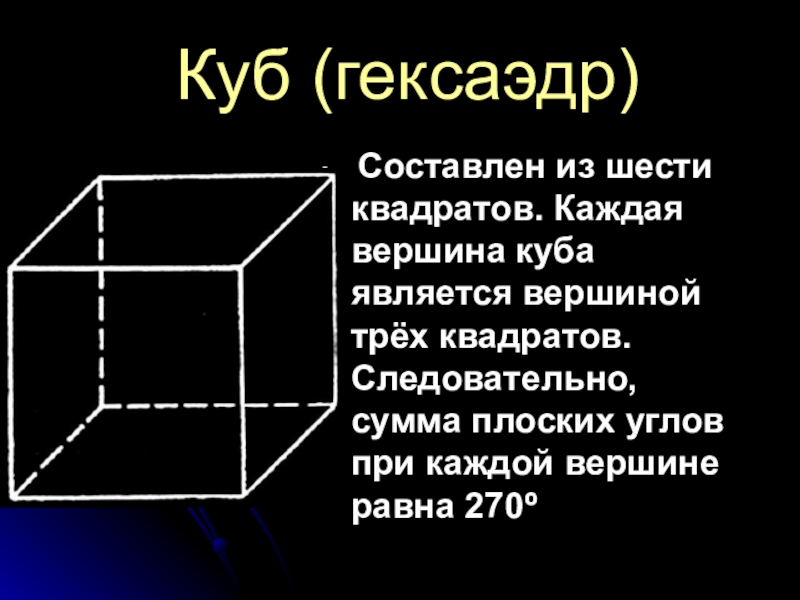
Слайд 16Куб (гексаэдр)
Составлен из шести квадратов. Каждая вершина куба является вершиной
трёх квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270º
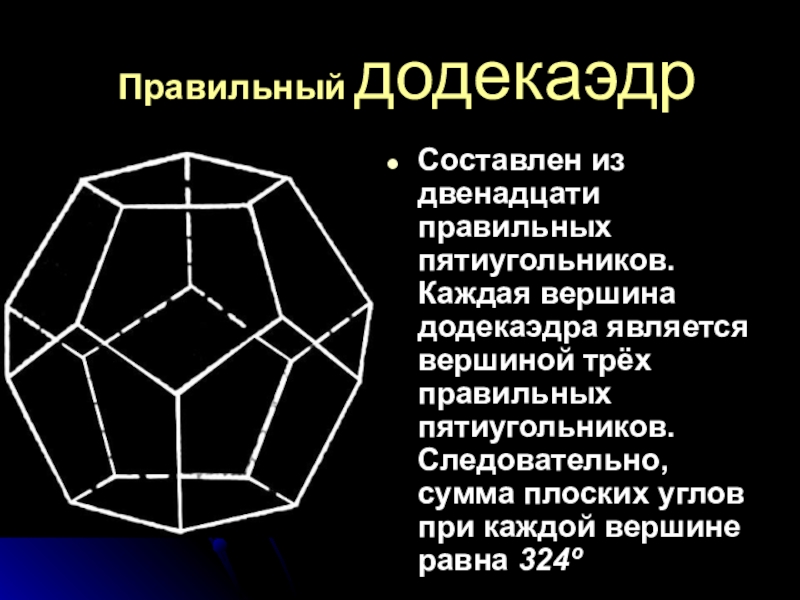
Слайд 17Правильный додекаэдр
Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной
трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324º
Слайд 18Названия многогранников
пришли из Древней Греции
в них указывается число граней:
эдра −
грань
тетра − 4
гекса − 6
окта − 8
икоса − 20
додека − 12
тетра − 4
гекса − 6
окта − 8
икоса − 20
додека − 12
Слайд 26Формула Эйлера
Сумма числа граней и вершин любого многогранника
равна числу рёбер,
увеличенному на 2.
Г + В = Р + 2
Г + В = Р + 2
Число граней плюс число вершин минус число рёбер
в любом многограннике равно 2.
Г + В − Р = 2
Слайд 28Задача: Определите количество граней, вершин и рёбер многогранника, изображённого на рисунке
. Проверьте выполнимость
формулы Эйлера для данного многогранника.
Слайд 30
Правильный октаэдр, правильный икосаэдр, правильный додекаэдр имеют центр симметрии и несколько
осей и плоскостей симметрии.