теоретического материала.
Решение задач на периметр и площадь.
Замечательные линии треугольника.
Подведение итогов.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Повторение. Периметр и площадь
Содержание
- 1. Повторение. Периметр и площадь
- 2. 1. Повторение.Прямоугольник Квадрат
- 3. 2. Решение задач.№1. Постройте в тетради параллелограмм
- 4. 2. Решение задач.№3. По чертежу найдите периметр
- 5. Высота и медиана треугольника.ha – высота, проведённая
- 6. Решение задач на вычисление медианы и высоты
- 7. Тема урока: Повторение. Периметр и площадь. Замечательные
1. Повторение.Прямоугольник Квадрат Параллелограмм Ромб Трапеция Периметр многоугольника – сумма длин всех сторон. Обозначается Р.Площадь находится как произведение двух величин: длины и ширины фигуры. Вопрос
Слайд 1Тема урока: Повторение. Периметр и площадь. Замечательные линии треугольника.
План работы:
Повторение
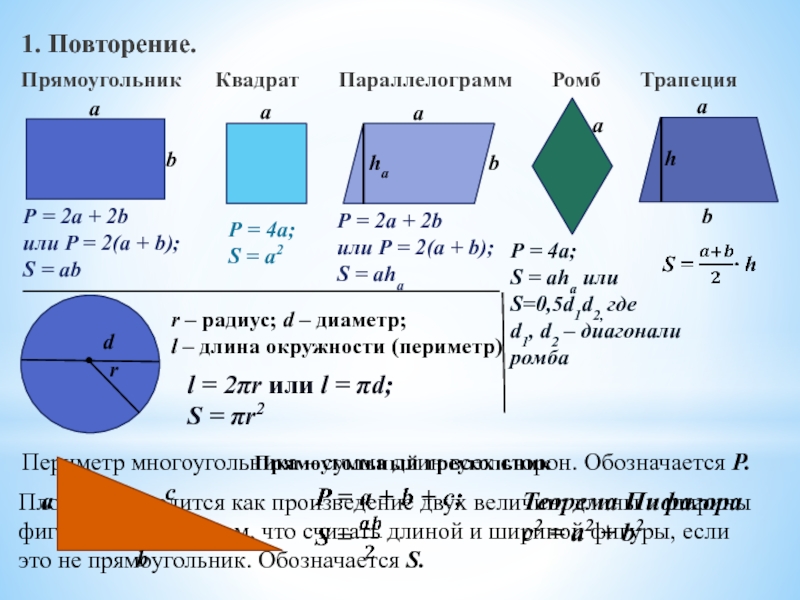
Слайд 21. Повторение.
Прямоугольник Квадрат Параллелограмм
Ромб Трапеция
Периметр многоугольника – сумма длин всех сторон. Обозначается Р.
Площадь находится как произведение двух величин: длины и ширины фигуры. Вопрос в том, что считать длиной и шириной фигуры, если это не прямоугольник. Обозначается S.
Р = 2a + 2b
или P = 2(a + b);
S = ab
Р = 4a;
S = a2
Р = 2a + 2b
или P = 2(a + b);
S = aha
Р = 4a;
S = aha или S=0,5d1d2, где
d1, d2 – диагонали ромба
r
d
r – радиус; d – диаметр;
l – длина окружности (периметр)
l = 2πr или l = πd;
S = πr2
Теорема Пифагора
с2 = a2 + b2
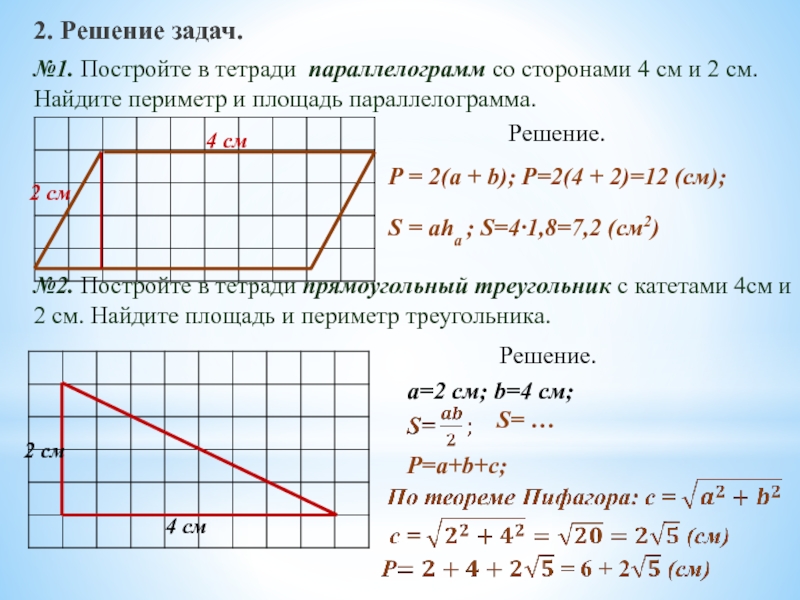
Слайд 32. Решение задач.
№1. Постройте в тетради параллелограмм со сторонами 4 см
и 2 см. Найдите периметр и площадь параллелограмма.
№2. Постройте в тетради прямоугольный треугольник с катетами 4см и 2 см. Найдите площадь и периметр треугольника.
№2. Постройте в тетради прямоугольный треугольник с катетами 4см и 2 см. Найдите площадь и периметр треугольника.
P = 2(a + b); P=2(4 + 2)=12 (см);
S = aha ; S=4∙1,8=7,2 (см2)
4 см
2 см
2 см
4 см
Решение.
Решение.
a=2 см; b=4 см;
S= …
P=a+b+c;
Слайд 42. Решение задач.
№3. По чертежу найдите периметр и площадь фигуры.
Р=4а; Р=4∙3=12
(дм);
S=a2; S=32=9 (дм2)
Р=2(а+b); Р=2∙(2+4,5)=13 (см);
S=аb; S=2∙4,5=9 (см2)
a=2 см; b=8 см; h=2,2 см;
a=6 м; b=5 м; h=4 м;
Р=2(а+b); Р=2∙(6+5)=22 (м);
S = aha ;
S = 6∙4=24 (м2)
Р=4а; Р=4∙5=20 (см);
S=0,5d1d2,
S=0,5∙8∙6=24 (см2)
l = πd; S = πr2
l = π∙6=6π (см);
r = d:2; r = 3 см
S =π∙32= 9π (см2)
Слайд 5Высота и медиана треугольника.
ha – высота, проведённая к стороне а;
hb
– высота, проведённая к стороне b;
hc – высота, проведённая к стороне c;
mc – медиана, проведённая к стороне c;
mb – медиана, проведённая к стороне b;
ma – медиана, проведённая к стороне a;
3. Замечательные линии треугольника
Слайд 6Решение задач на вычисление медианы и высоты треугольника.
Найдите указанные высоту и
медиану, если известны стороны треугольника:
a=5, b=6, c=7; ma; ha -? 2) a=6, b=8, c=10; mc; hc-?
3) a=6, b=10, c=12; mc; hb-? 4) a=5, b=12, c=13; mc; hc-?
5) a=7, b=9, c=10; mb; hb-?
a=5, b=6, c=7; ma; ha -? 2) a=6, b=8, c=10; mc; hc-?
3) a=6, b=10, c=12; mc; hb-? 4) a=5, b=12, c=13; mc; hc-?
5) a=7, b=9, c=10; mb; hb-?
р – a = 9-5 = 4;
p – b = 9-6 = 3;
p – c = 9-7 = 2;
=>
2. a=6, b=8,c=10;mc; hc-?Подсказка: определите сначала вид треугольника.
a2 +b2 =c2 ;
62 +82 =102 ; 36+64=100 – верно, значит Δ прямоугольный с катетами 6 и 8.
Тема урока: Повторение. Периметр и площадь.
Слайд 7Тема урока: Повторение. Периметр и площадь. Замечательные линии треугольника.
План работы:
Повторение
теоретического материала.
Решение задач на периметр и площадь.
Замечательные линии треугольника.
Подведение итогов.
Решение задач на периметр и площадь.
Замечательные линии треугольника.
Подведение итогов.
