- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Подготовка к ГИА 11 класс геометрия задание 13(базовый уровень)
Содержание
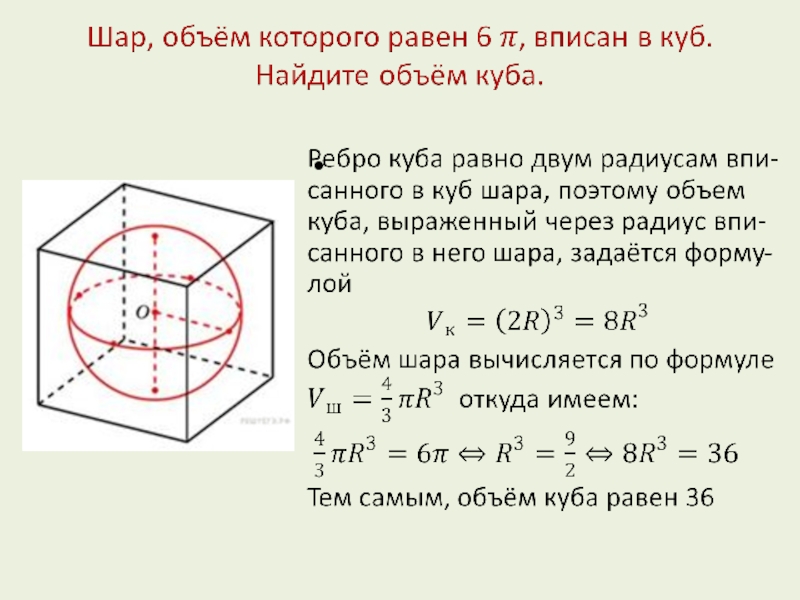
- 1. Подготовка к ГИА 11 класс геометрия задание 13(базовый уровень)
- 2. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
- 3.
- 4. Два ребра прямоугольного параллелепипеда, выходящие
- 5. Искомый объем равен разности объемов параллелепипеда со
- 6. В бак, имеющий форму правильной четырёхугольной призмы
- 7. Объем конуса равен 16. Через середину высоты
- 8. Во сколько раз увеличится площадь боковой поверхности
- 9. Меньший конус подобен большему с коэффициентом 0,5.
Слайд 1Подготовка к ГИА
Геометрия
Задание 13(базовый уровень)
Подготовила материал учитель математики – Кочерга Галина
МБОУ СОШ № 46, г. Хабаровск
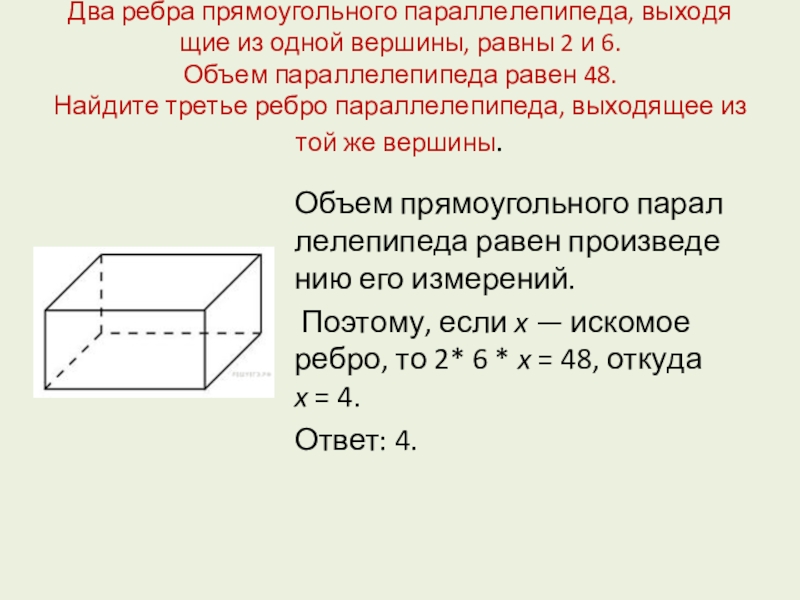
Слайд 4 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и
Объем прямоугольного параллелепипеда равен произведению его измерений.
Поэтому, если x — искомое ребро, то 2* 6 * x = 48, откуда x = 4.
Ответ: 4.
Слайд 5
Искомый объем равен разности объемов параллелепипеда со сторонами a, b и
Слайд 6В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной
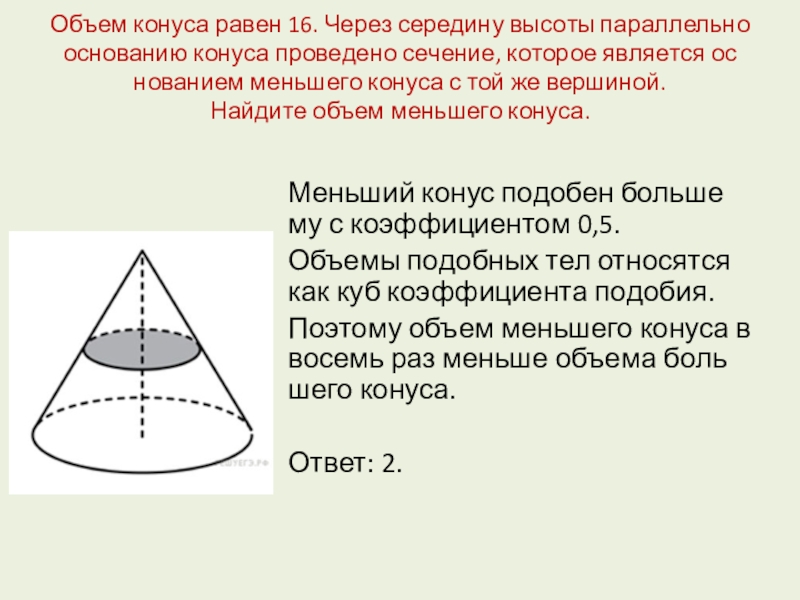
Слайд 7Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено
Меньший конус подобен большему с коэффициентом 0,5.
Объемы подобных тел относятся как куб коэффициента подобия.
Поэтому объем меньшего конуса в восемь раз меньше объема большего конуса.
Ответ: 2.
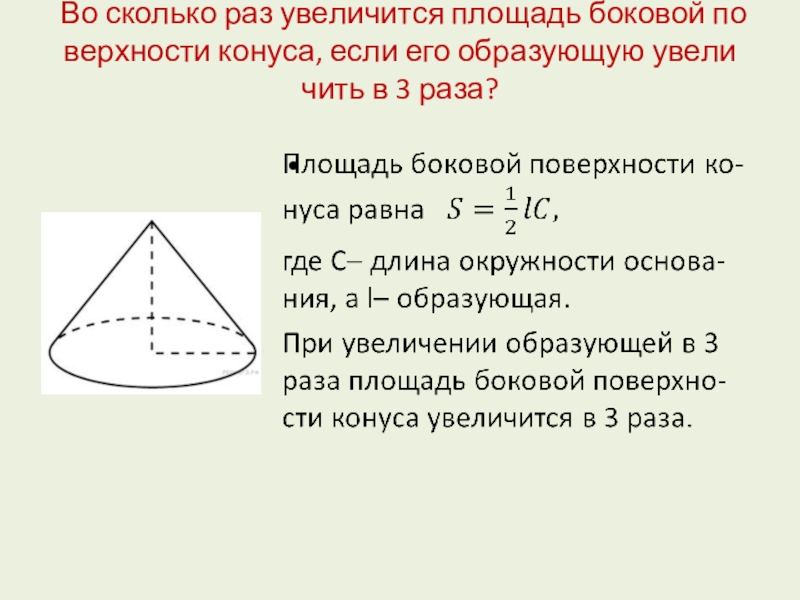
Слайд 8Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую
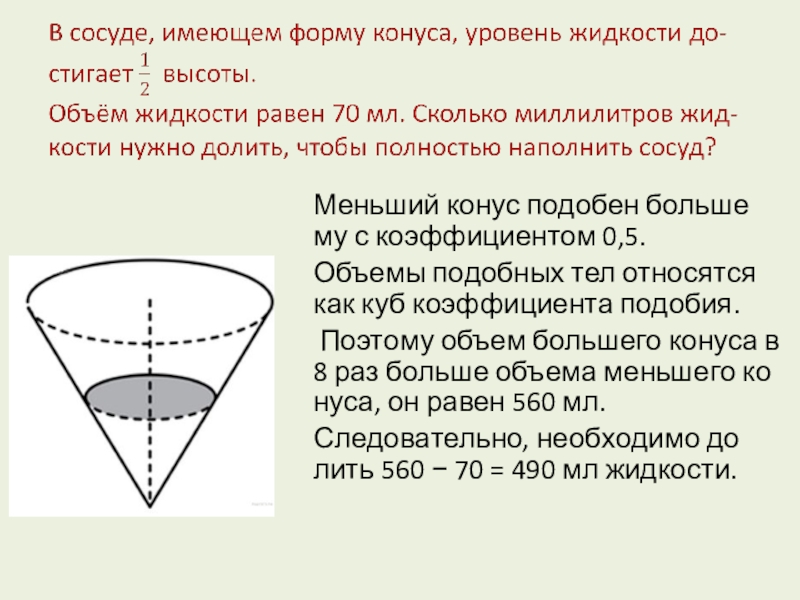
Слайд 9
Меньший конус подобен большему с коэффициентом 0,5.
Объемы подобных тел относятся
Поэтому объем большего конуса в 8 раз больше объема меньшего конуса, он равен 560 мл.
Следовательно, необходимо долить 560 − 70 = 490 мл жидкости.