- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему ПЛОЩАДЬ СЕГМЕНТА И ПЛОЩАДЬ СЛОЯ
Содержание
- 1. ПЛОЩАДЬ СЕГМЕНТА И ПЛОЩАДЬ СЛОЯ
- 2. Круговой сегмент-часть круга, ограниченная дугой окружности
- 3. Необходимо из площади сектора
- 4. Из площади круга вычитаем площадь полученного нами
- 5. где n – градусная мера центрального угла,
- 6. Круговой слой-это часть круга , заключенная
- 7. Из площади круга вычитаем две площади кругового сегмента: Формула площади кругового слоя
- 8. Формула площади кругового слоя
- 9. Условие : Прямая, проходящая
- 10. Решение
- 11. Условие: В круг радиуса 12
- 12. Решение:
- 13. Условие: Диаметр круга радиуса 12 см.
- 14. Решение:Сначала найдём длины трёх частей:2х+2х+4х=12х=1,5 ⇒ первая
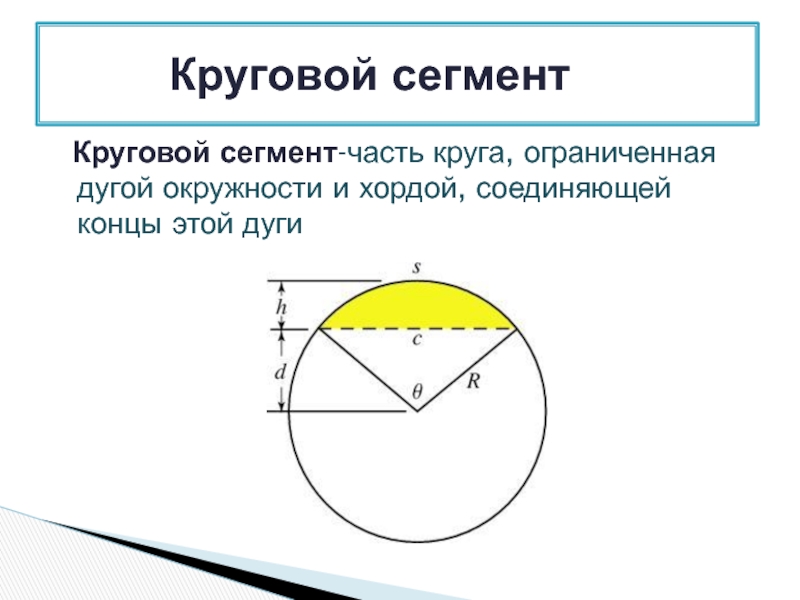
Слайд 2 Круговой сегмент-часть круга, ограниченная дугой окружности и хордой, соединяющей концы
Круговой сегмент
Слайд 3
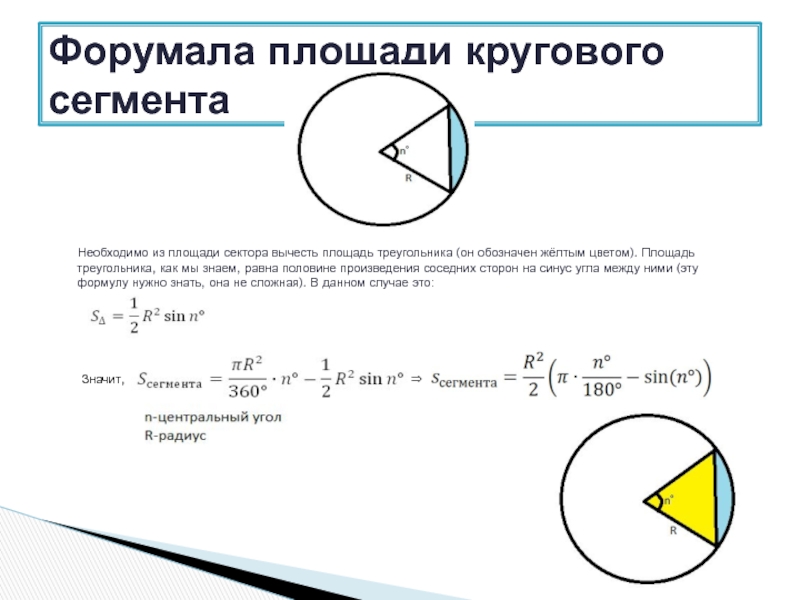
Необходимо из площади сектора вычесть площадь треугольника (он
Значит, ⇒
Форумала площади кругового сегмента
Слайд 4Из площади круга вычитаем площадь полученного нами сегмента:
360 – n градусов
Площадь сегмента, где центральный угол больше 180 градусов.
Слайд 5
где n – градусная мера центрального угла, который содержит дугу этого
Знак «минус» надо брать, когда n < 180˚, а знак «плюс» надо брать, когда n > 180˚.
Форумала площади кругового сегмента
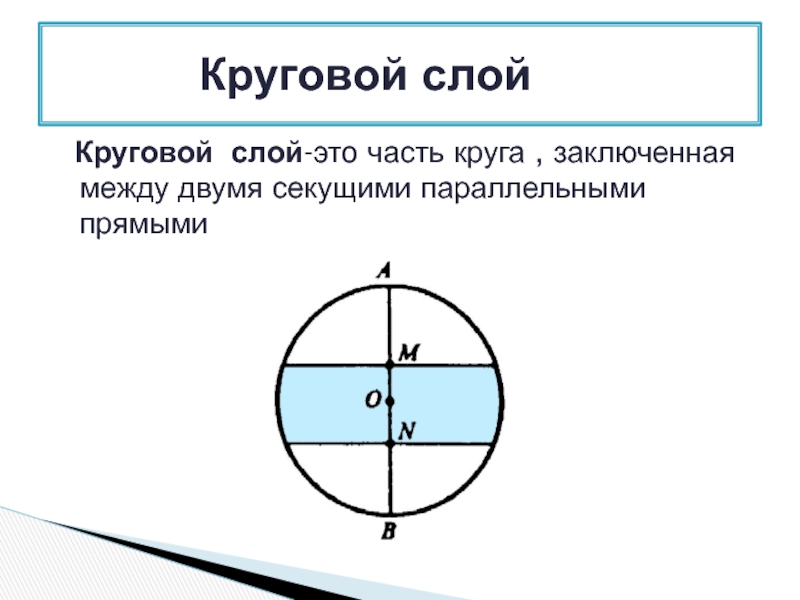
Слайд 6 Круговой слой-это часть круга , заключенная между двумя секущими параллельными
Круговой слой
Слайд 9 Условие :
Прямая, проходящая через точки A и B окружности, рассекает её
Задачи
Слайд 11 Условие:
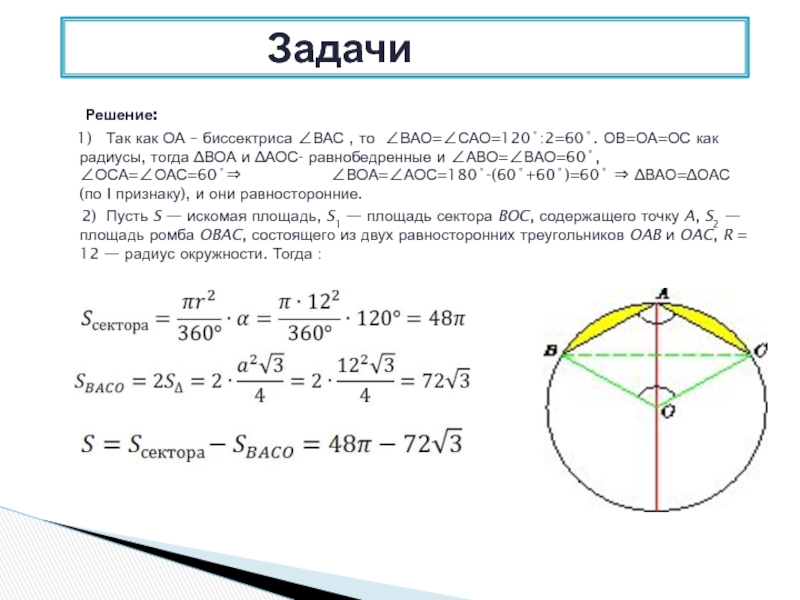
В круг радиуса 12 вписан угол величины 120o так, что
Задачи
Слайд 12
Решение:
1) Так как
2) Пусть S — искомая площадь, S1 — площадь сектора BOC, содержащего точку A, S2 —площадь ромба OBAC, состоящего из двух равносторонних треугольников OAB и OAC, R = 12 — радиус окружности. Тогда :
Задачи
Слайд 13 Условие:
Диаметр круга радиуса 12 см. разделен на 3 части,
Задачи
Слайд 14Решение:
Сначала найдём длины трёх частей:
2х+2х+4х=12
х=1,5 ⇒ первая и вторая часть круга
Теперь найдём угол γ:
γ=60˚⇒АВ=120˚
Теперь подставляем в формулу :
Задачи