- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Пезентация по геометрии на тему Четырехугольники в окружающем мире ( 8 класс )
Содержание
- 1. Пезентация по геометрии на тему Четырехугольники в окружающем мире ( 8 класс )
- 2. цели урокацели урока
- 3. Математическая сказкаМы закончили изучение темы: «Четырехугольники». Сегодня
- 4. … Собрались все четырёхугольники на лесной поляне
- 5. Вопросы: Кто стал королём? Кто был основным его соперником? Кто первым вышел из соревнования? квадратпрямоугольниктрапеция
- 6. Загадка Параллелограмма ABCD30160Найди ошибку!РешениеТ.К
- 7. Загадка Прямоугольника‹1 = 50Найти: ‹2, ‹3.ПодсказкаLN ?
- 8. Загадки РомбаBD = ABНайти углы ромбаПодсказкаAB ?
- 9. Загадка Квадрата Найти: ‹ 1,‹ 2.12АВСDРешениеТ.к. АВСD
- 10. По горизонтали: 5. Четырёхугольник, у которого противоположные
- 11. Слайд 11
- 12. КвадратПараллелограммПрямоугольникРомбАВСДОпределение: АВСД- четырёхугольник, АВ||CД,
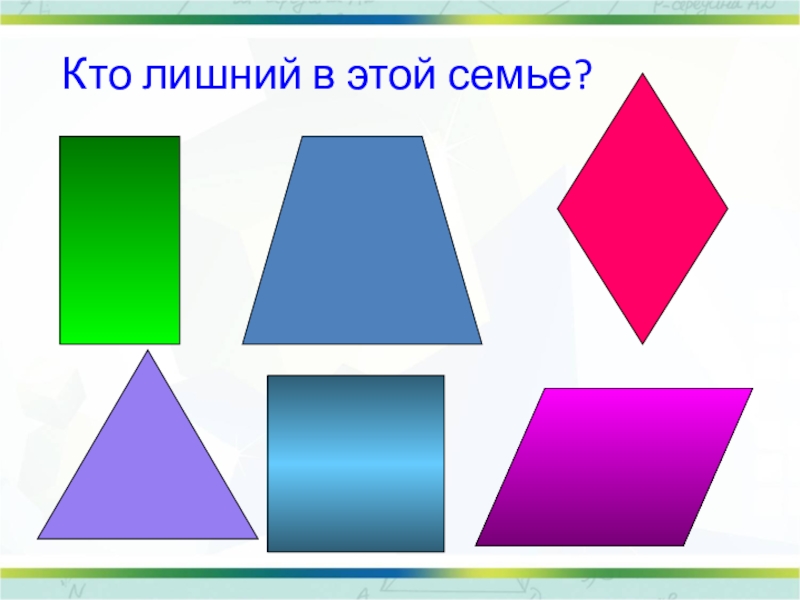
- 13. Кто лишний в этой семье?
- 14. «Тёмная лошадка»Знаете ли вы меня- , хочу
- 15. Термин «параллелограмм» греческого происхождения и согласно Проклу,
- 16. Слово «ромб» тоже греческого происхождения, оно означало
- 17. Термин «квадрат» происходит от латинского слова –
- 18. Прямоугольник в нашей жизни
- 19. Замечательное свойство прямоугольника Прямоугольник называется «золотым»,
- 20. Примеры «золотого» прямоугольникаБесконечное повторение одних
- 21. Русская сажень «Модулор» архитектора Корбюзье Примеры «золотого» прямоугольника
- 22. Давайте предположим, что жизнь человека в
- 23. В настоящее время уже есть опыт построения таких зданий
- 24. Выводы:Жизнь человека в настоящее время невозможна без
- 25. Тест по теории Вариант 1
- 26. иииилилли
- 27. Тест по теории Вариант 2
- 28. иилилииил
- 29. Математический диктант1.Верно ли, что каждый параллелограмм является
- 30. Игра «Догонялки»
- 31. Устная работа1.Чем отличаются свойства диагоналей прямоугольника от
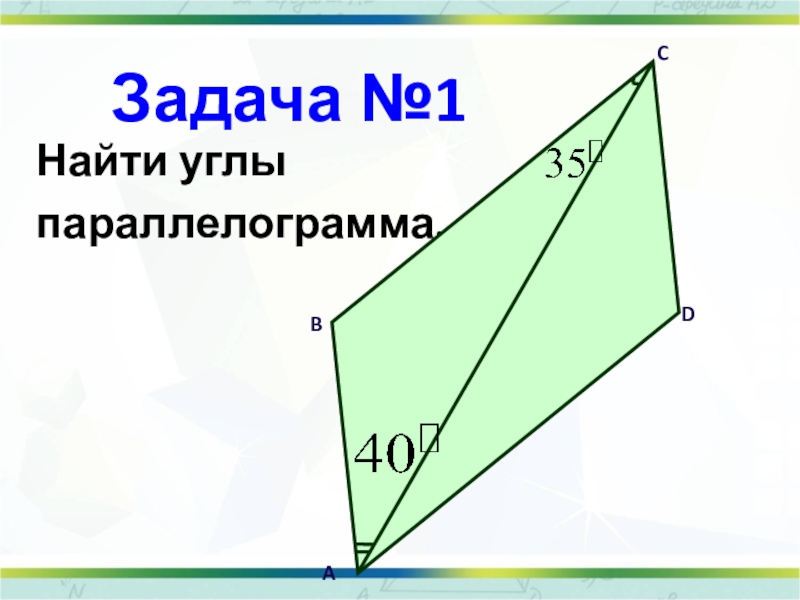
- 32. Задача №1Найти углы параллелограмма.ABCD
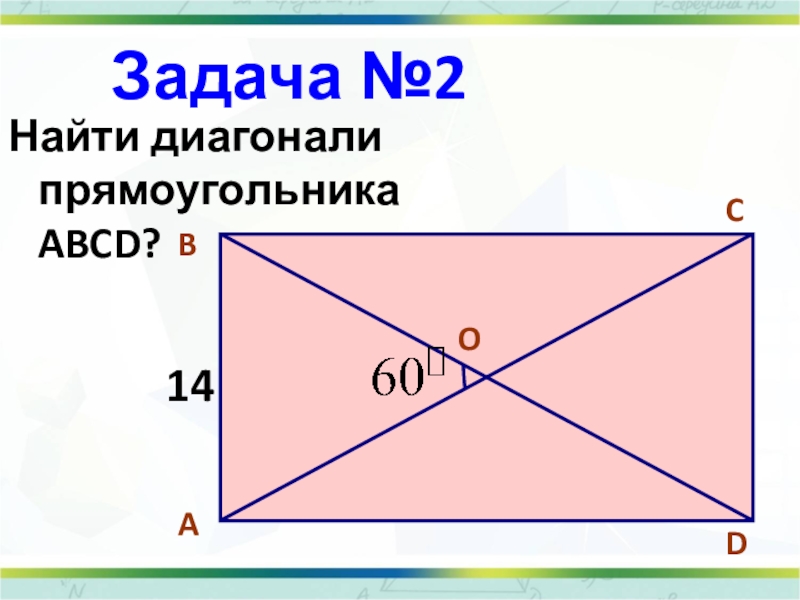
- 33. Задача №2Найти диагонали прямоугольника ABCD? OABCD14
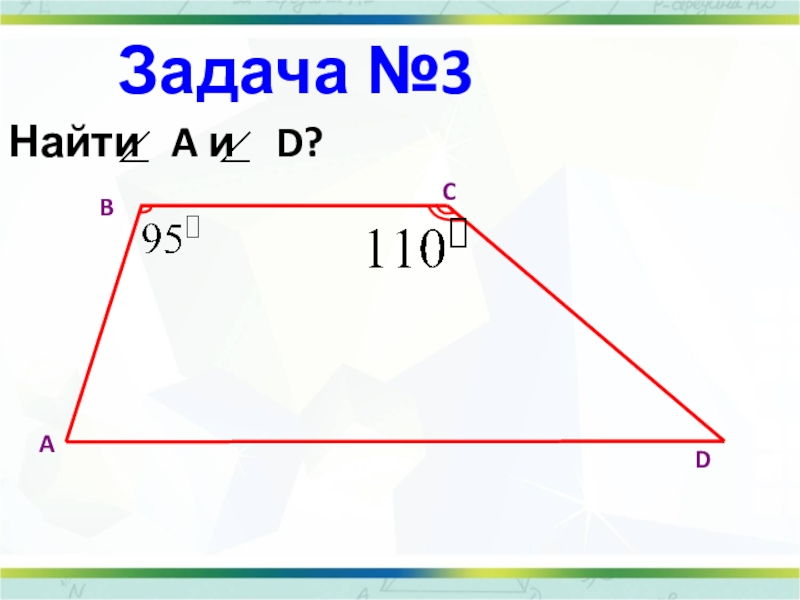
- 34. Задача №3Найти A и D? ABCD
- 35. Подведение итогов урока.Домашнее задание
Слайд 3Математическая сказка
Мы закончили изучение темы: «Четырехугольники». Сегодня еще раз вспомним определения
И расскажу я вам сказку, которая закончится вопросами. Сказки бывают волшебные, а наша еще и
полезная. Почему, потом поймете. Вы будете помогать мне. Как называется сказка, вы должны угадать.
Слайд 4… Собрались все четырёхугольники на лесной поляне и стали обсуждать вопрос
Слайд 5Вопросы:
Кто стал королём?
Кто был основным его соперником?
Кто первым
квадрат
прямоугольник
трапеция
Слайд 6
Загадка Параллелограмма
A
B
C
D
30
160
Найди ошибку!
Решение
Т.К АВСD- параллелограмм (по условию),
‹ А и ‹ В – внутренние односторонние углы при параллельных прямых ВС и АD, секущей АВ (по определению),
‹ А + ‹ В = 180 (по свойству)
150
Слайд 7Загадка Прямоугольника
‹1 = 50
Найти: ‹2, ‹3.
Подсказка
LN ? KM ? LO
∆ LOK ?
‹2 ? ‹3 ?
‹1 + ‹2 + ‹3 = ? ‹2 + ‹3 = ?
K
L
M
N
1
3
2
О
Решение
Т.к. LMNK – прямоугольник (по условию),
LN = KM, LN ∩ KM = О, KO = OM = LO = KO (по свойству),
∆ LOK–равнобедренный с основанием KL(по определению),
то ‹2 = ‹3 (по свойству)
‹1 + ‹2 + ‹3 = 180 (по свойству),
‹2 + ‹3 = 130 ,
‹2 = ‹3 = 65
65
65
Слайд 8Загадки Ромба
BD = AB
Найти углы ромба
Подсказка
AB ? AD ?
∆ ADВ
‹1 ?
Решение
∆ ADB-равносторонний(по опр.), ‹ 1+‹2+‹3= 180 (по свойству),значит,‹1=‹2=‹3=60
Т.к. АВСD – ромб (по условию), а диагонали ромба являются биссектрисами его углов(по свойству), то ‹ А = ‹ С = 60 и ‹ В = ‹ D = 120 (по свойству)
А
D
В
С
60
120
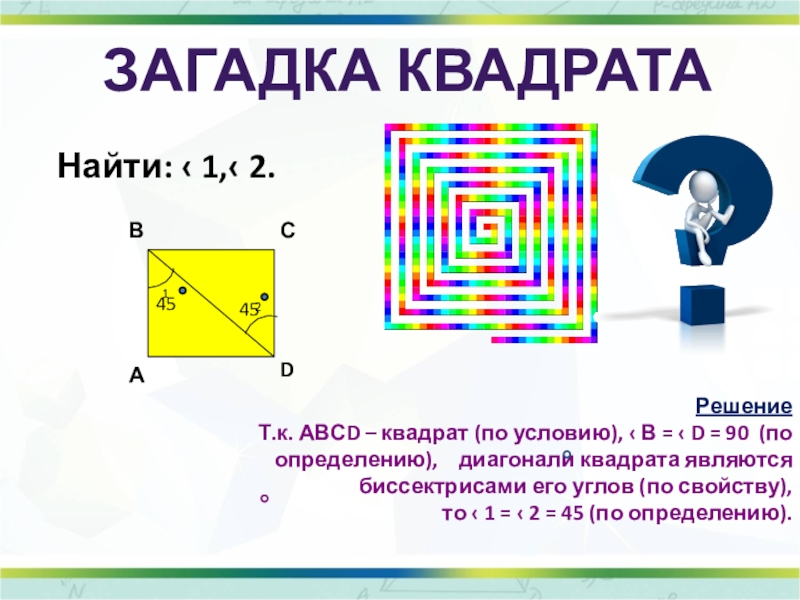
Слайд 9Загадка Квадрата
Найти: ‹ 1,‹ 2.
1
2
А
В
С
D
Решение
Т.к. АВСD – квадрат (по условию),
то ‹ 1 = ‹ 2 = 45 (по определению).
45
45
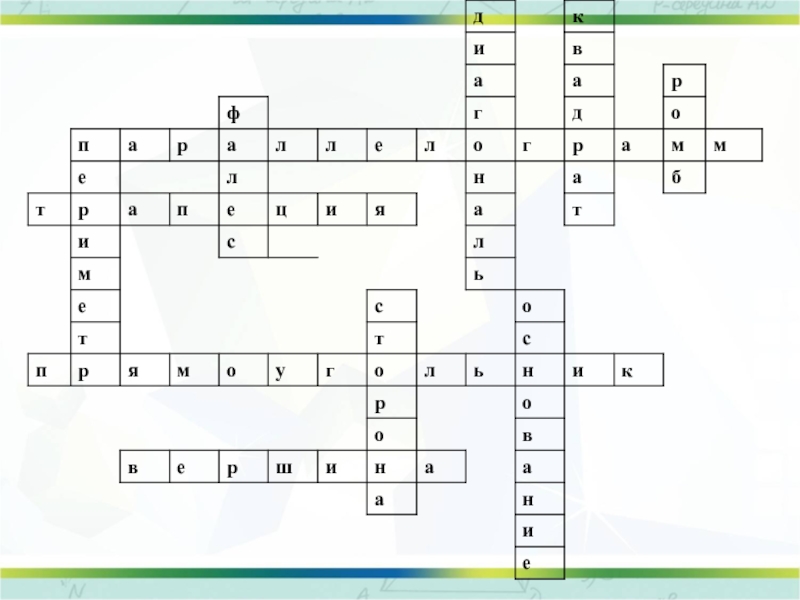
Слайд 10По горизонтали:
5. Четырёхугольник, у которого противоположные стороны параллельны.
6. Четырёхугольник, у
9. Параллелограмм, у которого все углы прямые.
10. Точки, из которых выходят стороны четырёхугольников.
По вертикали:
1. Отрезок, соединяющий противолежащие вершины четырёхугольника.
2. Прямоугольник, у которого все стороны равны.
3. Параллелограмм, у которого все стороны равны.
4. Древнегреческий ученый из Милета.
5.Сумма длин всех сторон многоугольника.
7. Отрезок, соединяющий соседние вершины четырёхугольника.
8. Одна из параллельных сторон трапеции.
Разгадай кроссворд
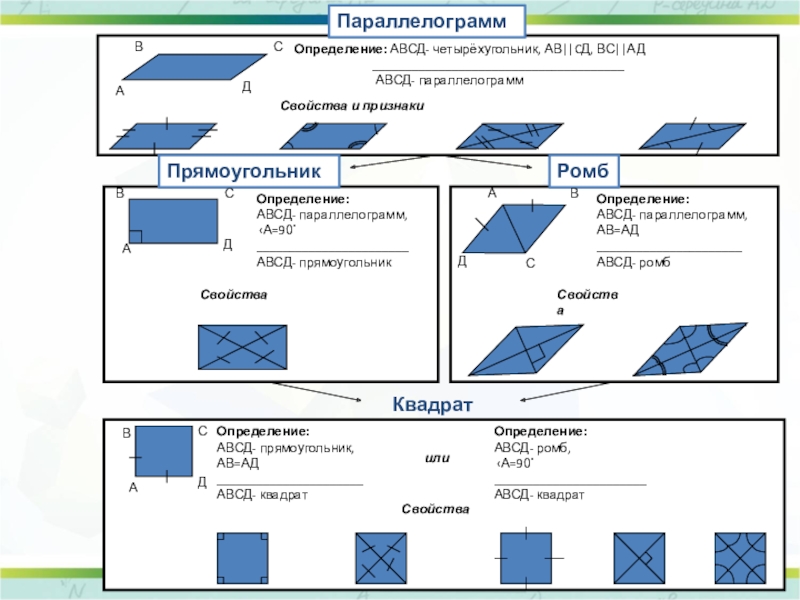
Слайд 12 Квадрат
Параллелограмм
Прямоугольник
Ромб
А
В
С
Д
Определение: АВСД- четырёхугольник, АВ||CД, ВС||АД
АВСД- параллелограмм
Определение:
АВСД- параллелограмм,
‹А=90ْ
_______________________
АВСД- прямоугольник
Свойства и признаки
А
В
С
Д
Свойства
Определение:
АВСД- параллелограмм,
АВ=АД
______________________
АВСД- ромб
А
В
С
Д
Свойства
Определение:
АВСД- прямоугольник,
АВ=АД
______________________
АВСД- квадрат
или
Определение:
АВСД- ромб,
‹А=90ْ
_______________________
АВСД- квадрат
Свойства
А
В
С
Д
Слайд 14«Тёмная лошадка»
Знаете ли вы меня- , хочу проверить.
Любую площадь я могу
Ведь у меня четыре стороны
И все они между собой равны.
И у меня равны все диагонали,
Углы мне они делят пополам и ими
На части равные разбит я сам.
Слайд 15
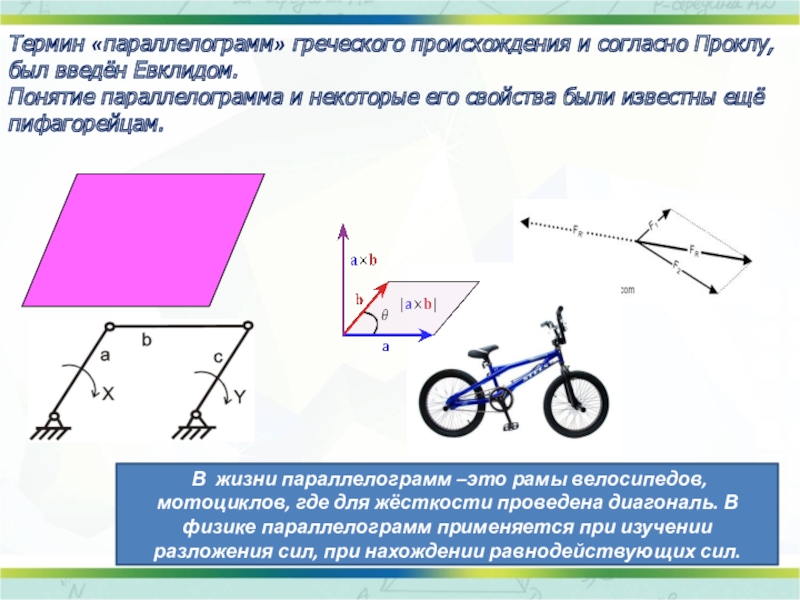
Термин «параллелограмм» греческого происхождения и согласно Проклу, был введён Евклидом.
Понятие параллелограмма
В жизни параллелограмм –это рамы велосипедов, мотоциклов, где для жёсткости проведена диагональ. В физике параллелограмм применяется при изучении разложения сил, при нахождении равнодействующих сил.
Слайд 16Слово «ромб» тоже греческого происхождения, оно означало в древности вращающееся тело,
Реечный домкрат для легковых автомобилей имеет форму ромба. Плиточники укладывают плитку в виде ромба
Слайд 17Термин «квадрат» происходит от латинского слова – сделать четырёхугольным.
«Первый четырёхугольник, с
Д. Мордухай-Болтовский.
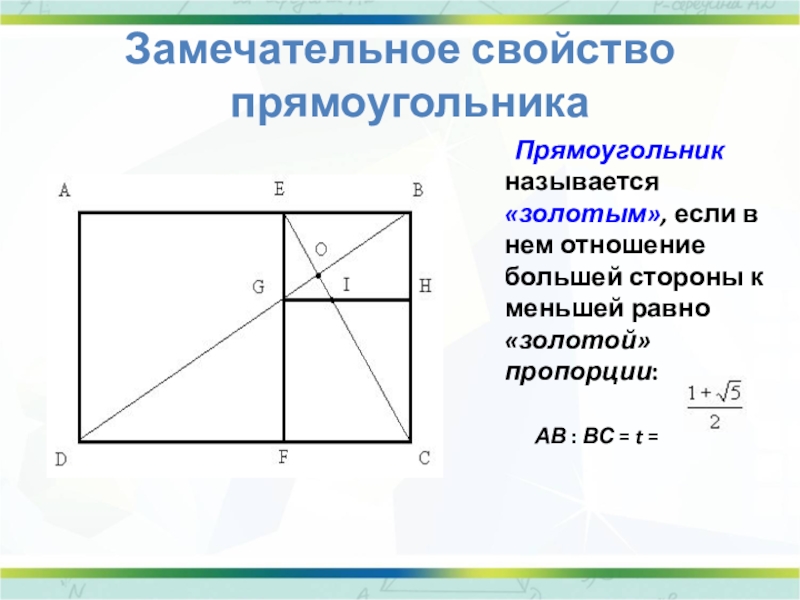
Слайд 19Замечательное свойство
прямоугольника
Прямоугольник называется «золотым», если в нем отношение большей
АВ : ВС = t =
Слайд 20Примеры «золотого»
прямоугольника
Бесконечное повторение одних и тех же геометрических фигур
Считается, что именно это является причиной того, что многие предметы прямоугольной формы, с которыми человек имеет дело часто имеют форму «золотого» прямоугольника. Свойство «золотого» прямоугольника используется в архитектуре и живописи.
«Золотое сечение»
в архитектуре
и живописи
Андрей Рублёв «Святая троица»
Детская головоломка
Слайд 22Давайте предположим, что
жизнь человека в будущем возможна без прямоугольников.
…Может быть,
Слайд 24Выводы:
Жизнь человека в настоящее время невозможна без прямоугольников.
Прямоугольники встречаются всюду:
Прямоугольная форма придаёт всем объектам устойчивость, равновесие, практичность, экономичность в использовании материалов, красоту.
Слайд 29Математический диктант
1.Верно ли, что каждый параллелограмм является ромбом?
2.Является ли прямоугольником параллелограмм,
3.Если две стороны четырёхугольника параллельны, а две другие нет, то он является трапецией?
4.Диагонали квадрата являются биссектрисами его углов?
5.У ромба и параллелограмма диагонали перпендикулярны?
6.Диагонали параллелограмма 5см и 5см. Является ли этот параллелограмм прямоугольником?
Ответ:
1.нет
2.да
3.да
4.да
5.нет
6.да
Слайд 31Устная работа
1.Чем отличаются свойства диагоналей прямоугольника от ромба?
Прямоугольник
1)… 1) -
2)- 2)…
3)- 3)…
2.Сумма двух углов параллелограмма 120 . Найти углы параллелограмма.
А
В
С
равны
перпендикулярны
‹ А = ‹ С = 60 (по свойству)
‹ А + ‹ С = 120 (по условию)
‹ В = ‹ D = 120 (по свойству)
D
Решение