- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Перпендикулярность прямых и плоскостей.Повторение
Содержание
- 1. Перпендикулярность прямых и плоскостей.Повторение
- 2. СтереометрияРаздел геометрии, в котором изучаются свойства фигур в пространстве.Основные фигуры в пространстве:АТочка.аПрямая.Плоскость.
- 3. Аксиомы стереометрии Через любые три точки,
- 4. Аксиомы стереометрии описывают:Способ задания плоскостиВзаимное расположение прямой и плоскостиВзаимное расположение плоскостей
- 5. Признак перпендикулярности прямой и плоскостиПрямая называется перпендикулярной
- 6. Теорема о прямой, перпендикулярной к плоскостиТЕОРЕМЫ,УСТАНАВЛИВАЮЩИЕ СВЯЗЬ
- 7. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯАН – перпендикуляр,проведенный из точки
- 8. Теорема о трёх перпендикулярах.Прямая ,проведённая в плоскости
- 9. ПланиметрияСтереометрияУглом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из одной точки.Двугранный угол
- 10. Двугранным углом называется фигура, образованная прямой a
- 11. Угол РDEK Двугранный угол АВNМ, где ВN
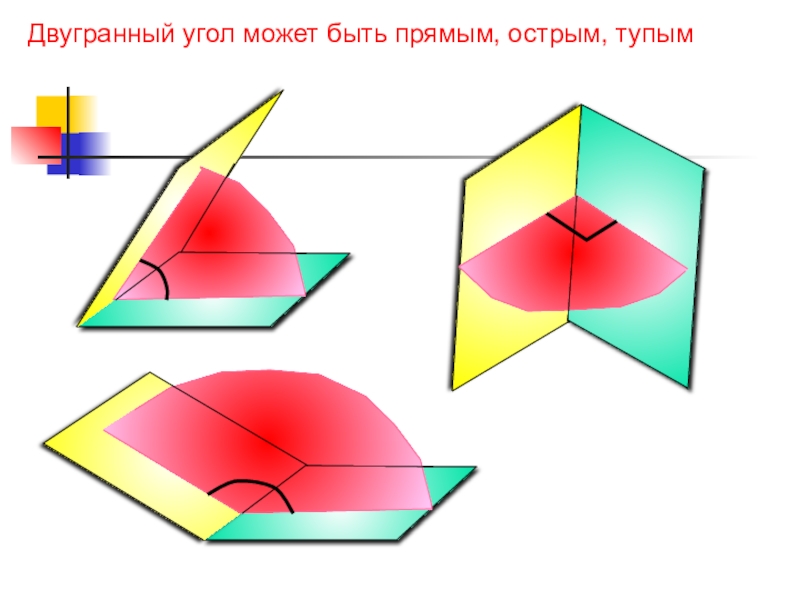
- 12. Двугранный угол может быть прямым, острым, тупым
- 13. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ :Если одна из
- 14. ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕДПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД – это параллелепипед, у
- 15. Прямоугольный параллелепипедABCDA1B1D1-ПАРАЛЛЕЛЕПИПЕДABCD u A1B1C1D1-основания(прямоугольника)АА1,ВВ1 ,СС1 ,DD1-боковые рёбра,АВВ1А1-боковая грань (прямоугольник)
- 16. Свойства прямоугольного параллелепипеда В прямоугольном параллелепипеде все шесть граней-прямоугольникиВсе двухгранные углы прямоугольного параллелепипеда-прямые
- 17. ТеоремаКвадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измеренийВДано:Доказать:ABCDA1B1D1Прямоугольный параллелепипед
- 18. Следствие:Диагонали прямоугольного параллелепипеда равны
- 19. Многогранный угол-это фигура,составленная из n плоских углов,не
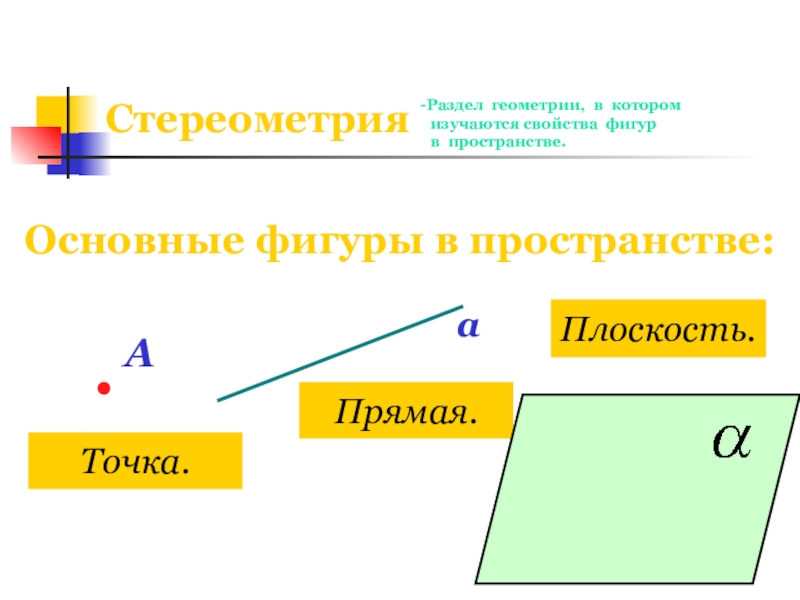
Слайд 2Стереометрия
Раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные
А
Точка.
а
Прямая.
Плоскость.
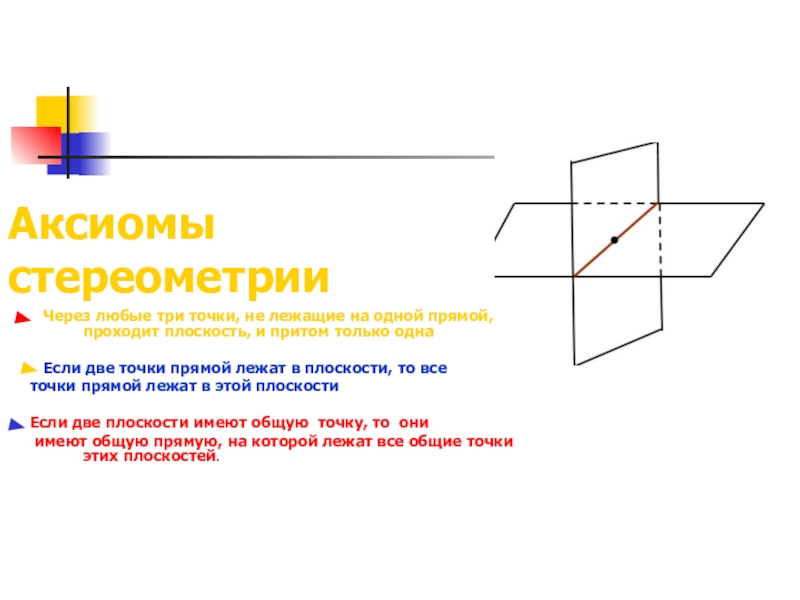
Слайд 3Аксиомы
стереометрии
Через любые три точки, не лежащие на одной прямой,
Если две точки прямой лежат в плоскости, то все
точки прямой лежат в этой плоскости
Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие точки этих плоскостей.
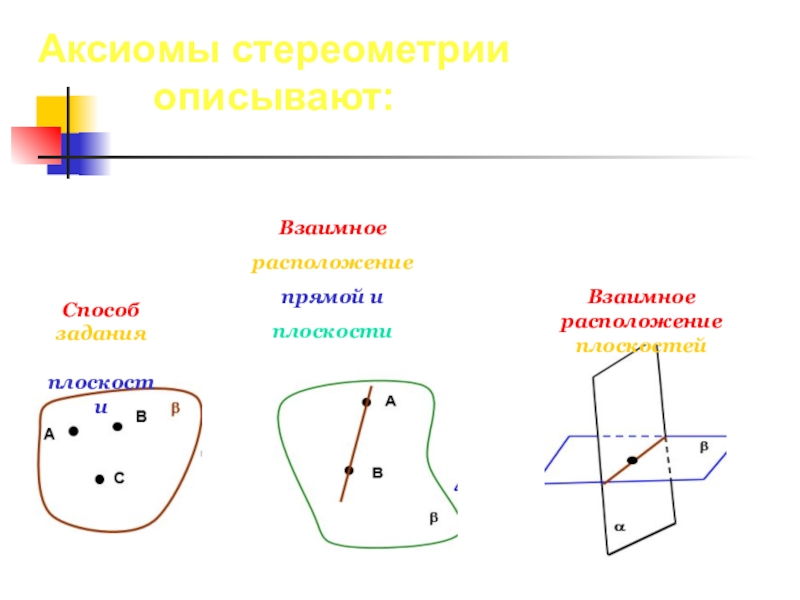
Слайд 4Аксиомы стереометрии описывают:
Способ
задания
плоскости
Взаимное
расположение
прямой и
плоскости
Взаимное расположение плоскостей
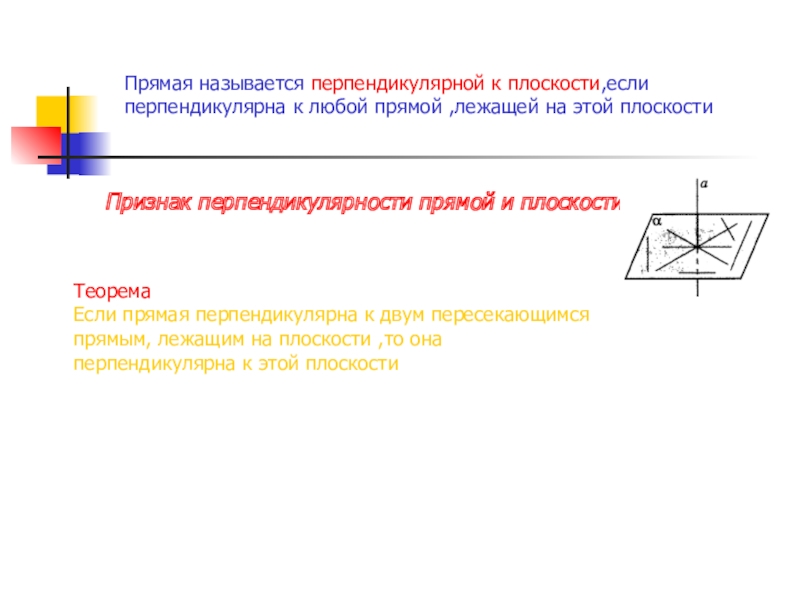
Слайд 5Признак перпендикулярности прямой и плоскости
Прямая называется перпендикулярной к плоскости,если перпендикулярна к
Теорема
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим на плоскости ,то она перпендикулярна к этой плоскости
Слайд 6Теорема о прямой, перпендикулярной к плоскости
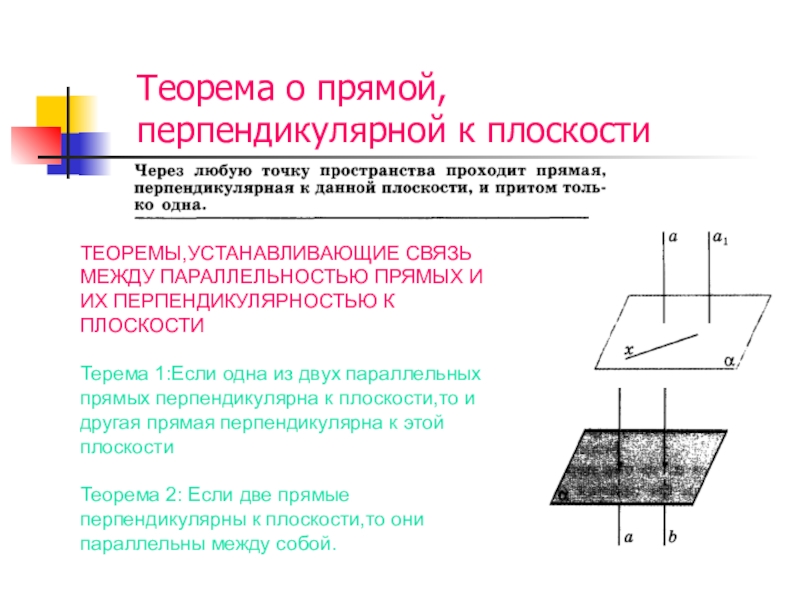
ТЕОРЕМЫ,УСТАНАВЛИВАЮЩИЕ СВЯЗЬ МЕЖДУ ПАРАЛЛЕЛЬНОСТЬЮ ПРЯМЫХ И
Терема 1:Если одна из двух параллельных прямых перпендикулярна к плоскости,то и другая прямая перпендикулярна к этой плоскости
Теорема 2: Если две прямые перпендикулярны к плоскости,то они параллельны между собой.
Слайд 7ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
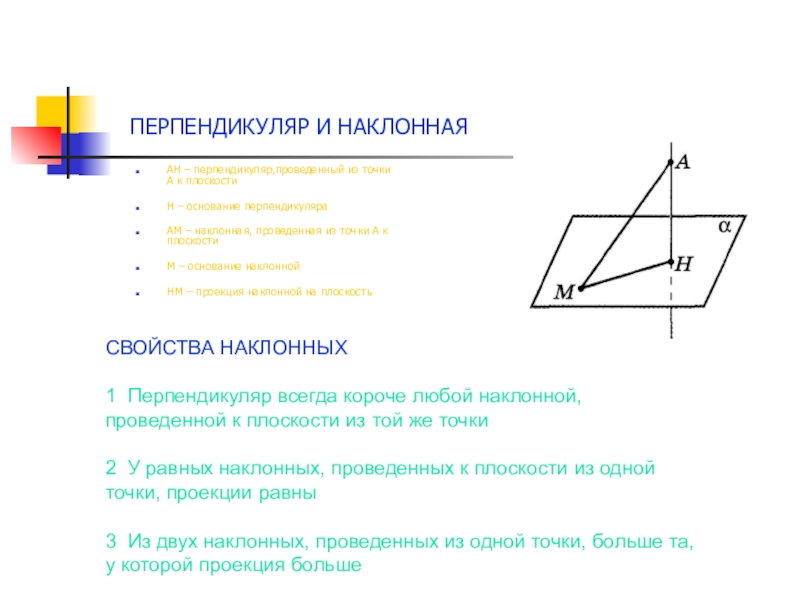
АН – перпендикуляр,проведенный из точки А к плоскости
Н
АМ – наклонная, проведенная из точки А к плоскости
М – основание наклонной
НМ – проекция наклонной на плоскость
СВОЙСТВА НАКЛОННЫХ
1 Перпендикуляр всегда короче любой наклонной, проведенной к плоскости из той же точки
2 У равных наклонных, проведенных к плоскости из одной точки, проекции равны
3 Из двух наклонных, проведенных из одной точки, больше та, у которой проекция больше
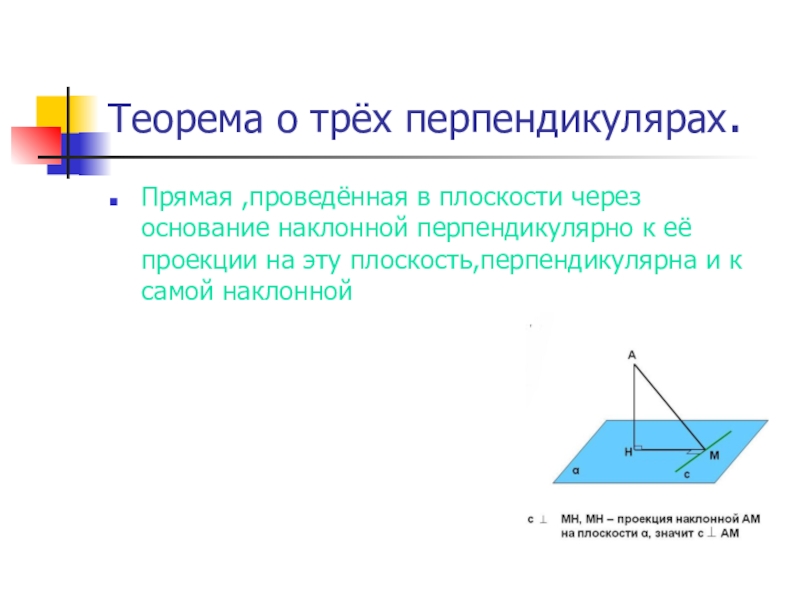
Слайд 8Теорема о трёх перпендикулярах.
Прямая ,проведённая в плоскости через основание наклонной перпендикулярно
Слайд 9
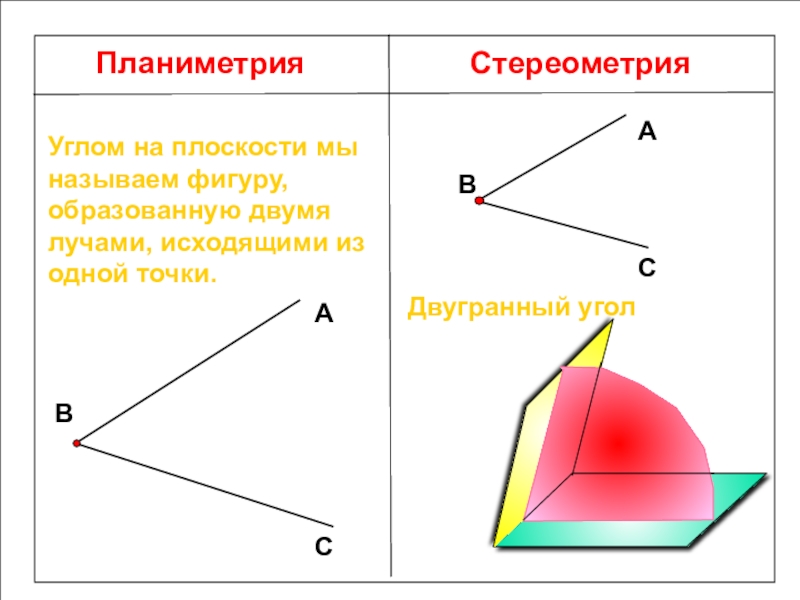
Планиметрия
Стереометрия
Углом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из
Двугранный угол
Слайд 10
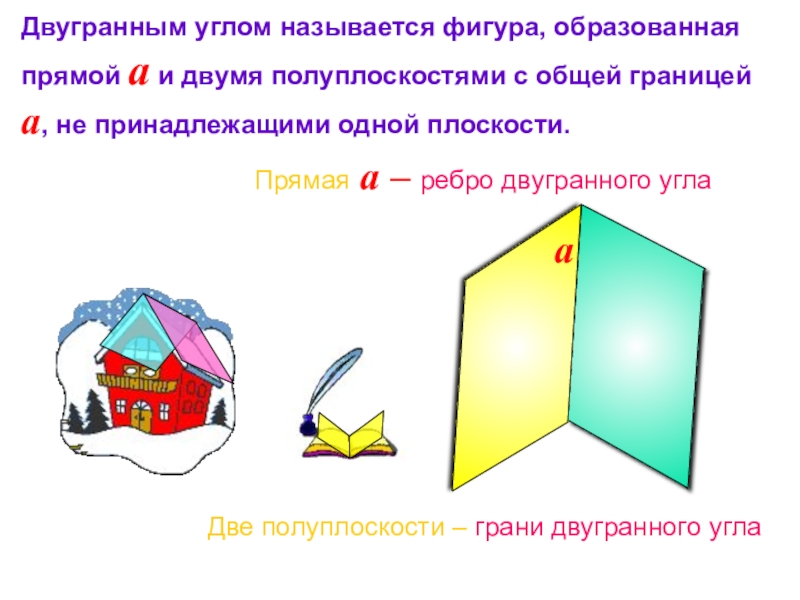
Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с
Две полуплоскости – грани двугранного угла
Прямая a – ребро двугранного угла
a
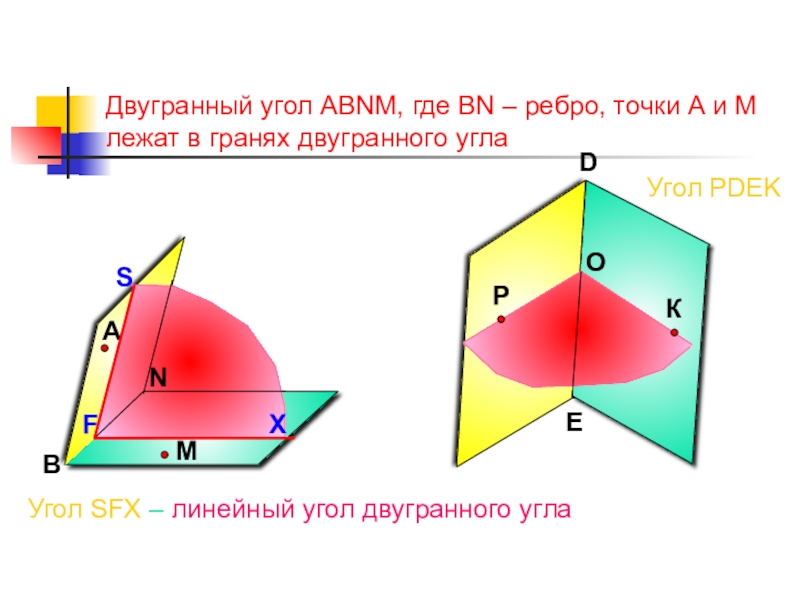
Слайд 11Угол РDEK
Двугранный угол АВNМ, где ВN – ребро, точки А
Угол SFX – линейный угол двугранного угла
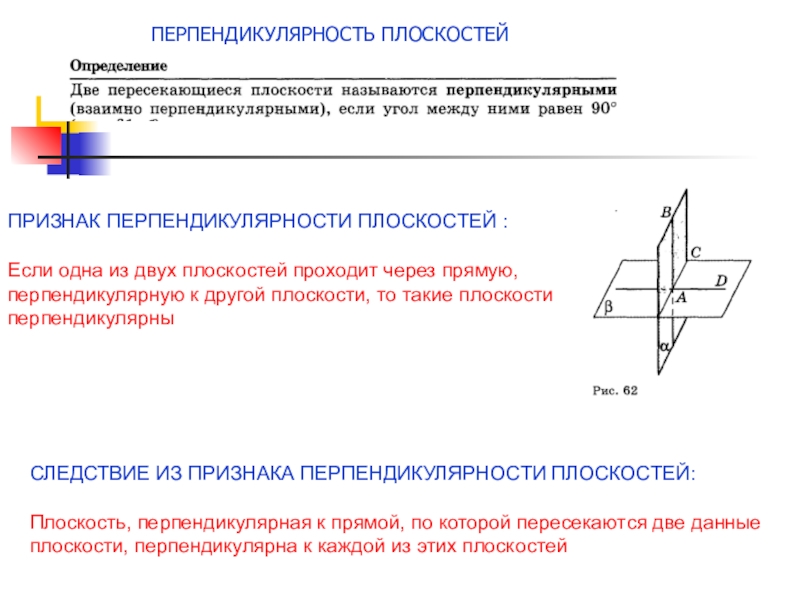
Слайд 13ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ :
Если одна из двух плоскостей проходит через
СЛЕДСТВИЕ ИЗ ПРИЗНАКА ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ:
Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей
Слайд 14ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД – это параллелепипед, у которого боковые рёбра перпендикулярны
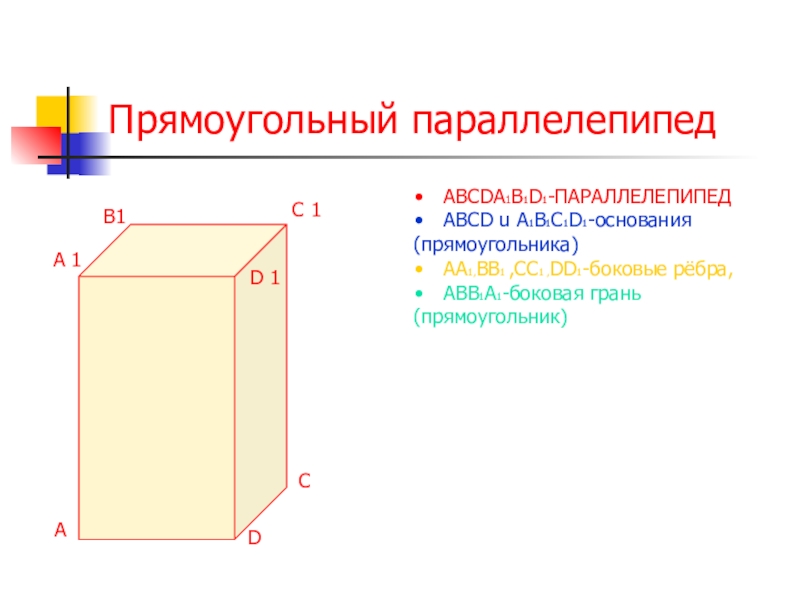
Слайд 15Прямоугольный параллелепипед
ABCDA1B1D1-ПАРАЛЛЕЛЕПИПЕД
ABCD u A1B1C1D1-основания
(прямоугольника)
АА1,ВВ1 ,СС1 ,DD1-боковые рёбра,
АВВ1А1-боковая грань
(прямоугольник)
Слайд 16Свойства прямоугольного параллелепипеда
В прямоугольном параллелепипеде все шесть граней-прямоугольники
Все двухгранные углы
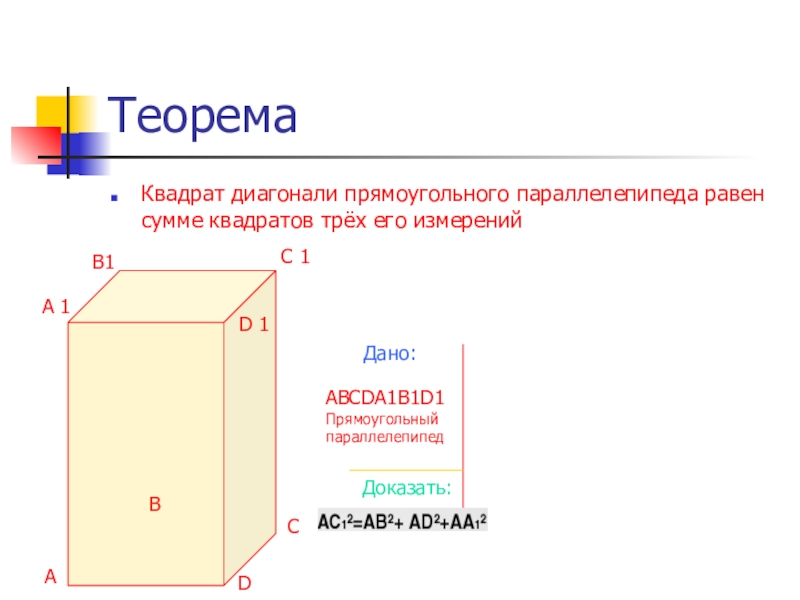
Слайд 17Теорема
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений
В
Дано:
Доказать:
ABCDA1B1D1
Прямоугольный
параллелепипед
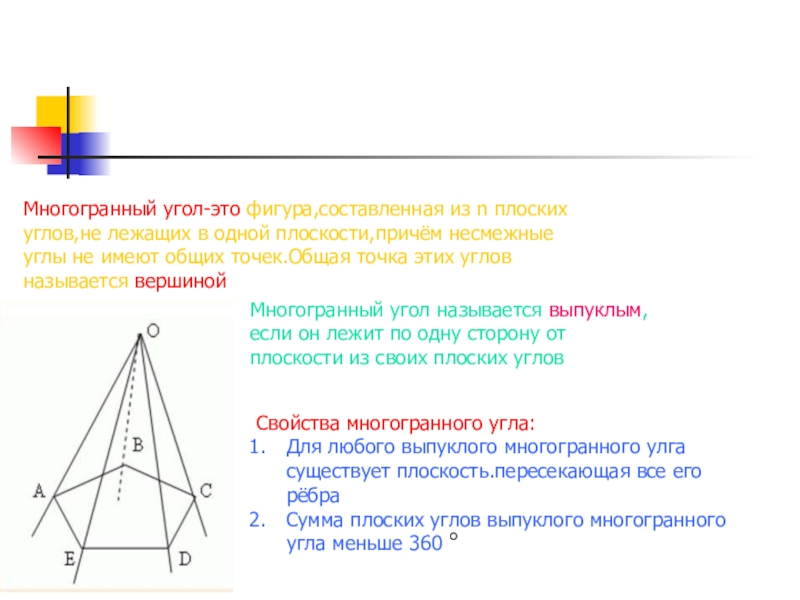
Слайд 19Многогранный угол-это фигура,составленная из n плоских углов,не лежащих в одной плоскости,причём
Многогранный угол называется выпуклым,если он лежит по одну сторону от плоскости из своих плоских углов
Свойства многогранного угла:
Для любого выпуклого многогранного улга существует плоскость.пересекающая все его рёбра
Сумма плоских углов выпуклого многогранного угла меньше 360