- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Параллелограмм. Его свойства и признаки.
Содержание
- 1. Параллелограмм. Его свойства и признаки.
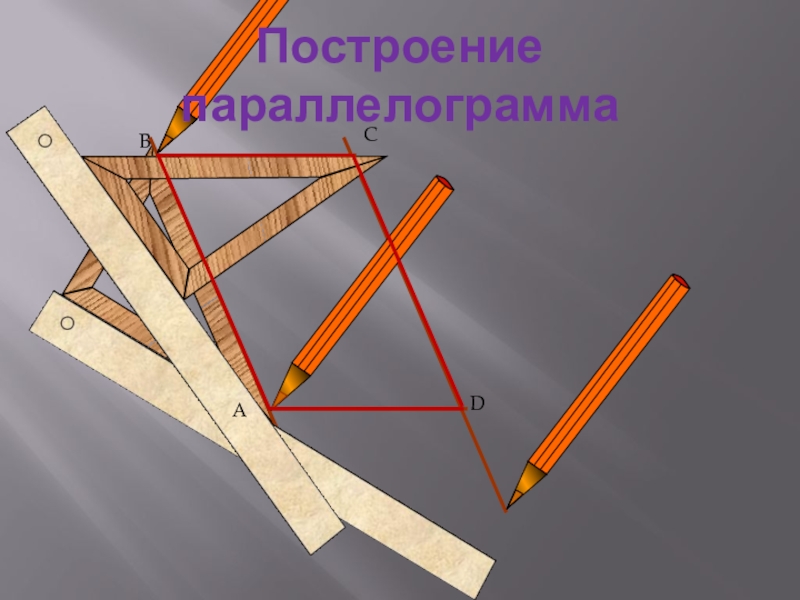
- 2. Построение параллелограммаАBCD
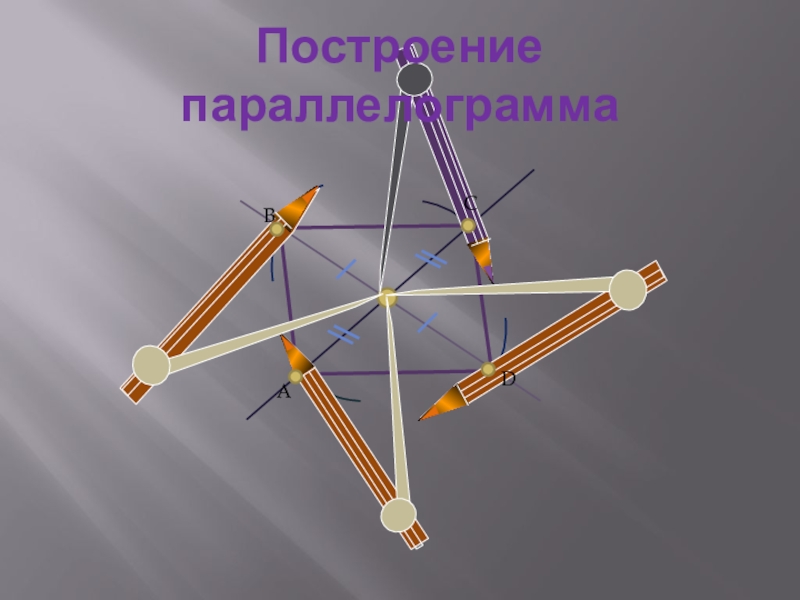
- 3. Построение параллелограммаАBCD
- 4. Параллелограмм — это четырёхугольник, у которого
- 5. CABDDABCТакже параллелограммом являются прямоугольник, квадрат и ромб.CABDПрямоугольник-это
- 6. Свойства 1.Противоположные стороны параллелограмма равны. |AB|=|CD|, |AD|=|BC|2.Противоположные углы параллелограмма равны.ABDCABDC
- 7. 3.Диагонали параллелограмма пересекаются и точкой пересечения делятся
- 8. 5.Точка пересечения диагоналей является центром симметрии параллелограмма.6.Сумма всех углов равна 360°23 14∠1+∠2+∠3+∠4=360º
- 9. Площадь параллелограмма.
- 10. У параллелограмма противолежащие стороны равны. Доказательство.
- 11. Свойство противолежащих углов параллелограмма. У параллелограмма противолежащие
- 12. дополнительные свойства параллелограмма
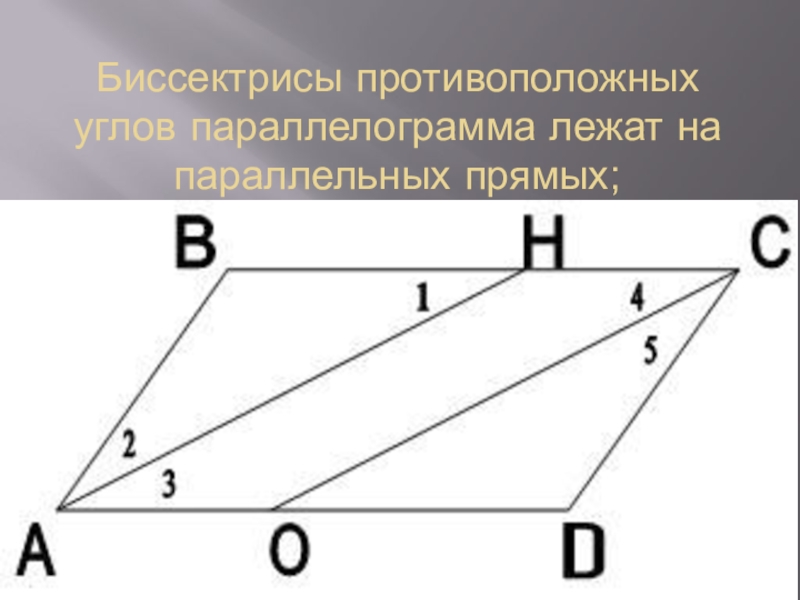
- 13. Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых;
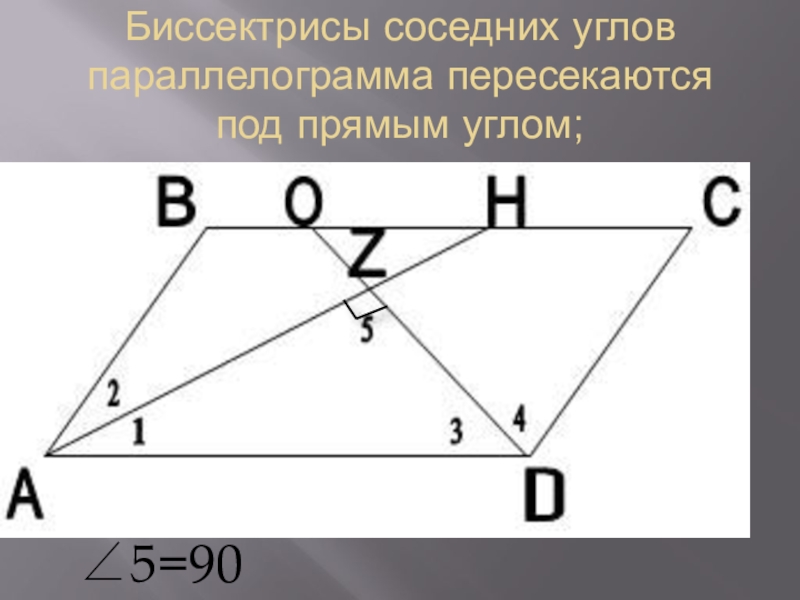
- 14. Биссектрисы соседних углов параллелограмма пересекаются под прямым углом;∠5=90о
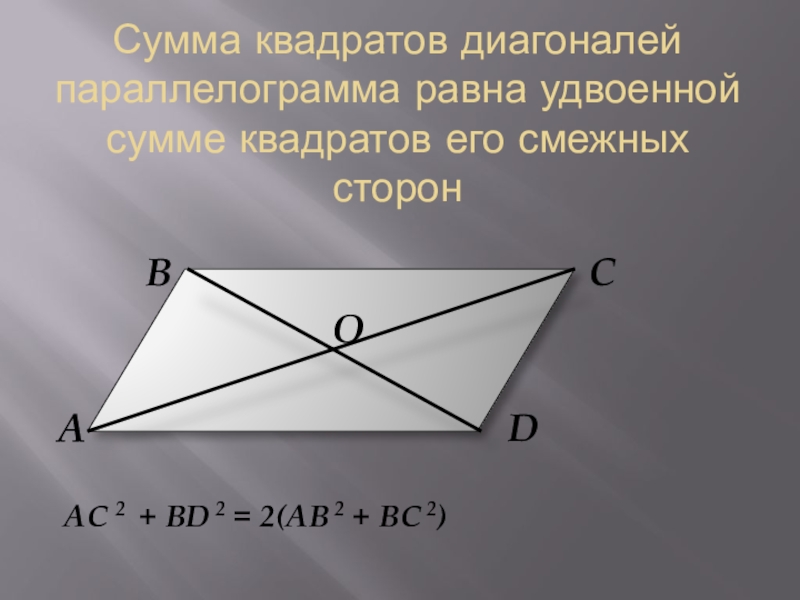
- 15. Сумма квадратов диагоналей параллелограмма равна удвоенной сумме
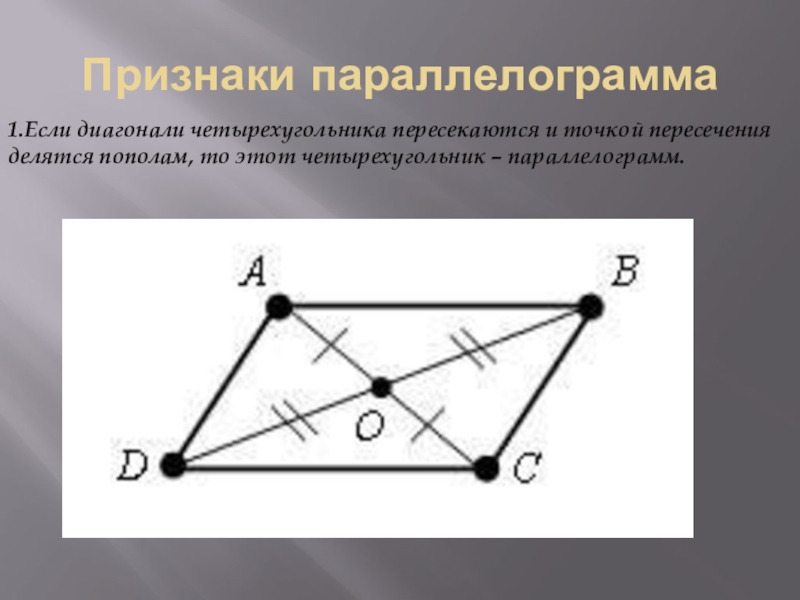
- 16. Признаки параллелограмма1.Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
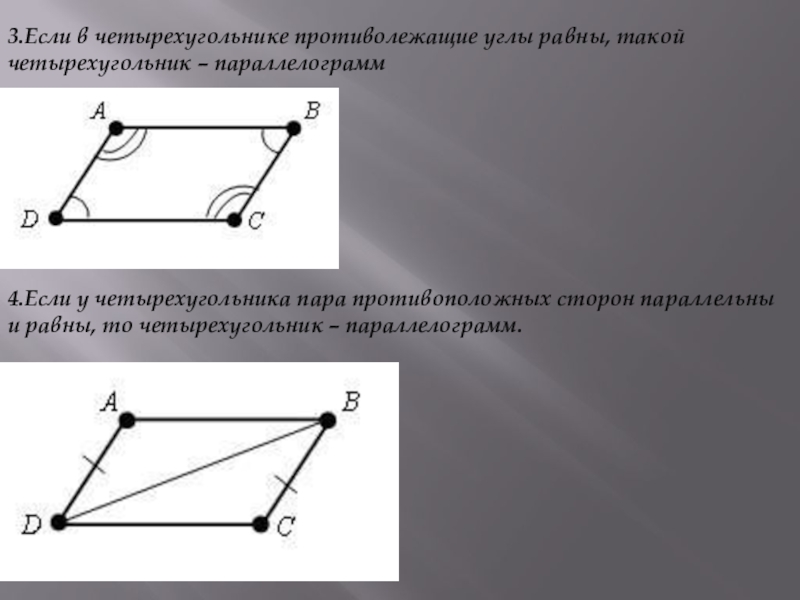
- 17. 3.Если в четырехугольнике противолежащие углы равны, такой
- 18. ПрименениеВ физике применяют параллелограмм при нахождении
- 19. Задача №1Найдите периметр параллелограмма, если биссектриса одного
- 20. Задача№1Найдите периметр параллелограмма, если биссектриса одного из
- 21. Задача№2С помощью циркуля и линейки разделите данный
- 22. Задача №3Периметр параллелограмма равен 16 см. Чему
- 23. Задача №4В параллелограмме ABCD диагональ BD =
Слайд 1Презентация
к уроку геометрии по теме «Параллелограмм. Его свойства и признаки».
Подготовила учитель
Слайд 4
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны,
A
B
D
C
Слайд 5C
A
B
D
D
A
B
C
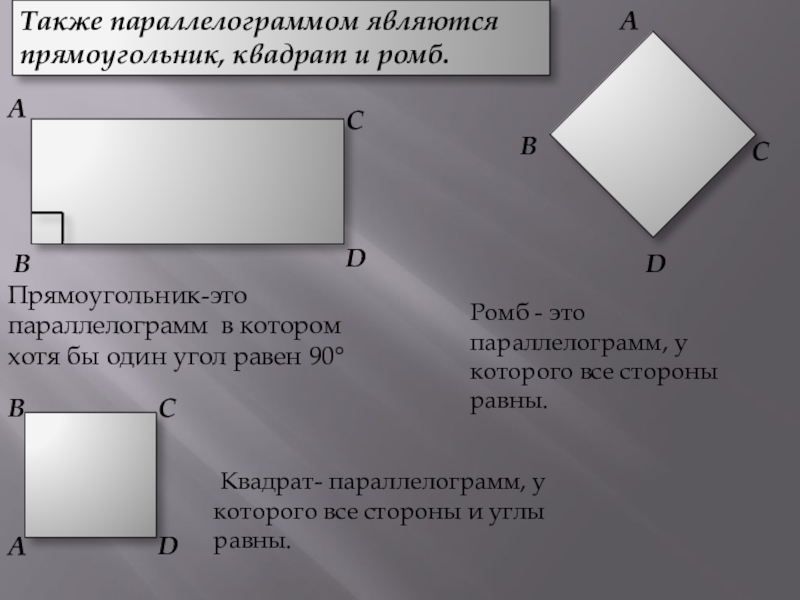
Также параллелограммом являются прямоугольник, квадрат и ромб.
C
A
B
D
Прямоугольник-это параллелограмм в котором хотя
Ромб - это параллелограмм, у которого все стороны равны.
Квадрат- параллелограмм, у которого все стороны и углы равны.
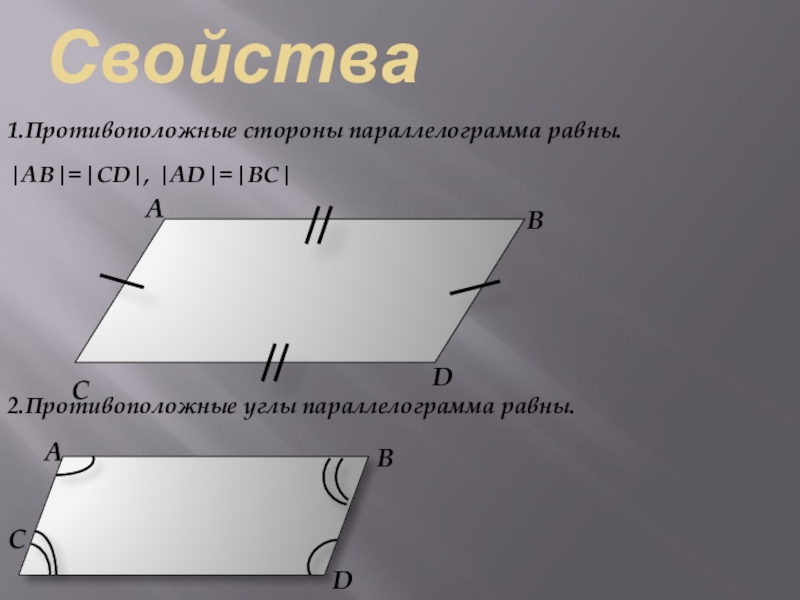
Слайд 6Свойства
1.Противоположные стороны параллелограмма равны.
|AB|=|CD|, |AD|=|BC|
2.Противоположные углы параллелограмма равны.
A
B
D
C
A
B
D
C
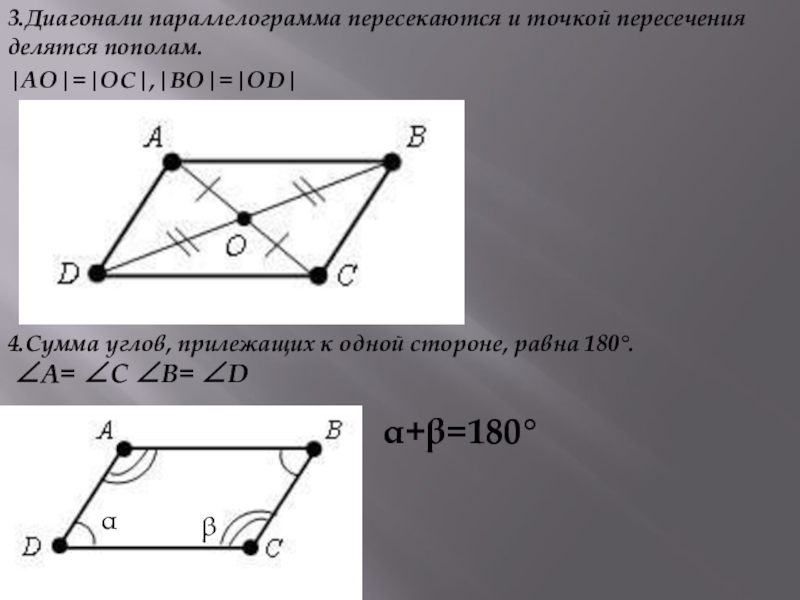
Слайд 73.Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
|AO|=|OC|,|BO|=|OD|
4.Сумма углов, прилежащих к
∠A= ∠C ∠B= ∠D
α
β
α+β=180°
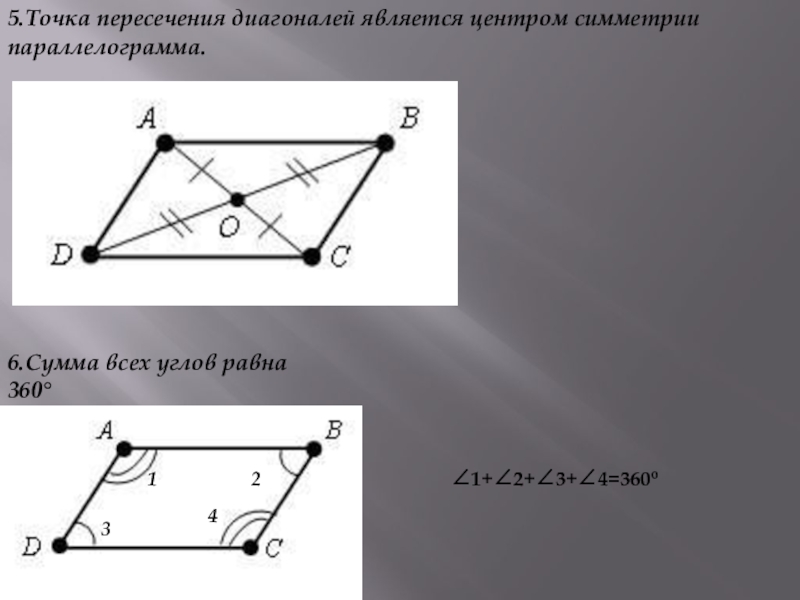
Слайд 85.Точка пересечения диагоналей является центром симметрии параллелограмма.
6.Сумма всех углов равна 360°
2
3
4
∠1+∠2+∠3+∠4=360º
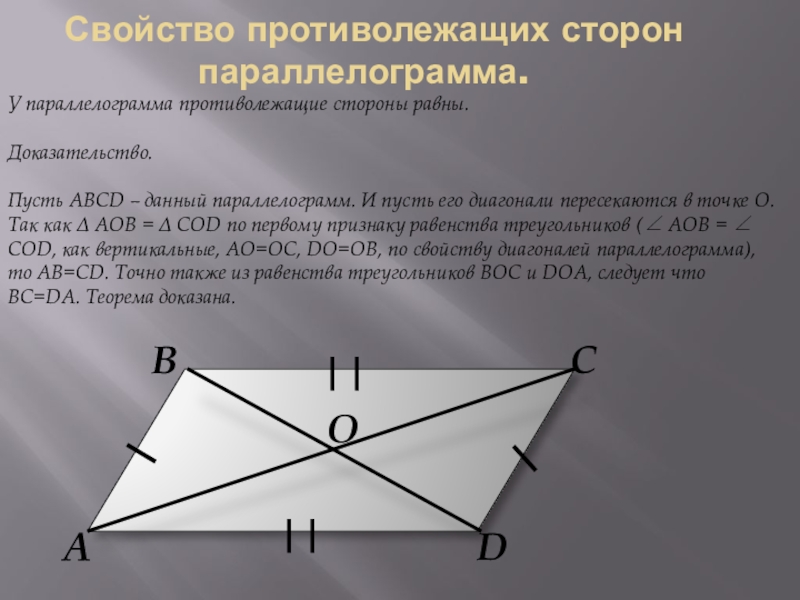
Слайд 10У параллелограмма противолежащие стороны равны.
Доказательство.
Пусть ABCD – данный параллелограмм. И пусть
A
B
C
D
O
||
||
|
|
Свойство противолежащих сторон параллелограмма.
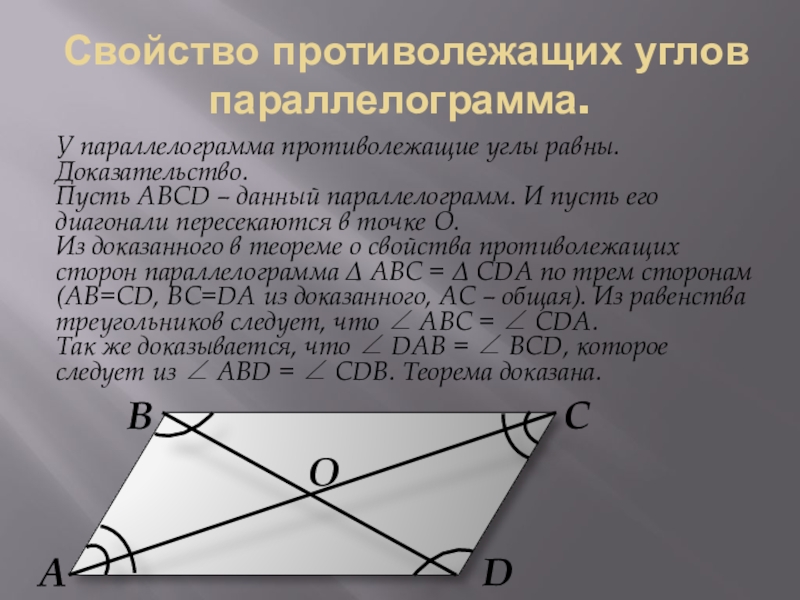
Слайд 11 Свойство противолежащих углов параллелограмма.
У параллелограмма противолежащие углы равны.
Доказательство.
Пусть ABCD – данный
O
A
B
C
D
Слайд 15Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон
A
B
C
D
O
AС
Слайд 16Признаки параллелограмма
1.Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то
Слайд 173.Если в четырехугольнике противолежащие углы равны, такой четырехугольник – параллелограмм
4.Если у
Слайд 18Применение
В физике применяют параллелограмм
при нахождении равнодействующей силы.
В жизни параллелограмм
Слайд 19Задача №1
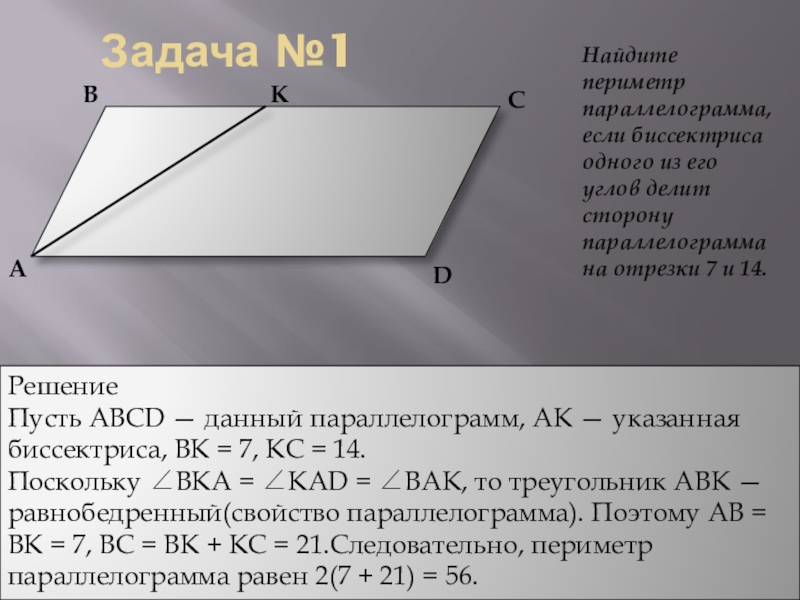
Найдите периметр параллелограмма, если биссектриса одного из его углов делит
Решение
Пусть ABCD — данный параллелограмм, AK — указанная биссектриса, BK = 7, KC = 14.
Поскольку ∠BKA = ∠KAD = ∠BAK, то треугольник ABK — равнобедренный(свойство параллелограмма). Поэтому AB = BK = 7, BC = BK + KC = 21.Следовательно, периметр параллелограмма равен 2(7 + 21) = 56.
A
B
C
D
K
Слайд 20Задача№1
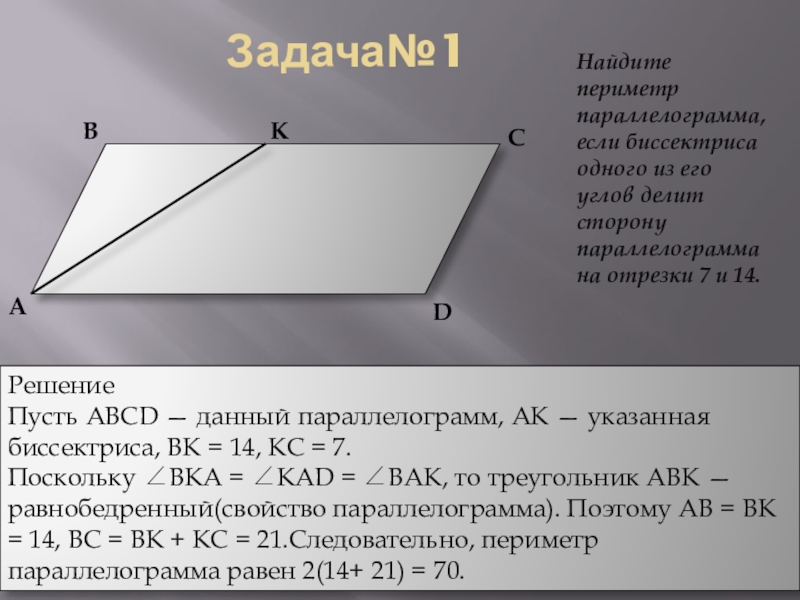
Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону
A
B
C
D
K
Решение
Пусть ABCD — данный параллелограмм, AK — указанная биссектриса, BK = 14, KC = 7.
Поскольку ∠BKA = ∠KAD = ∠BAK, то треугольник ABK — равнобедренный(свойство параллелограмма). Поэтому AB = BK = 14, BC = BK + KC = 21.Следовательно, периметр параллелограмма равен 2(14+ 21) = 70.
Слайд 21Задача№2
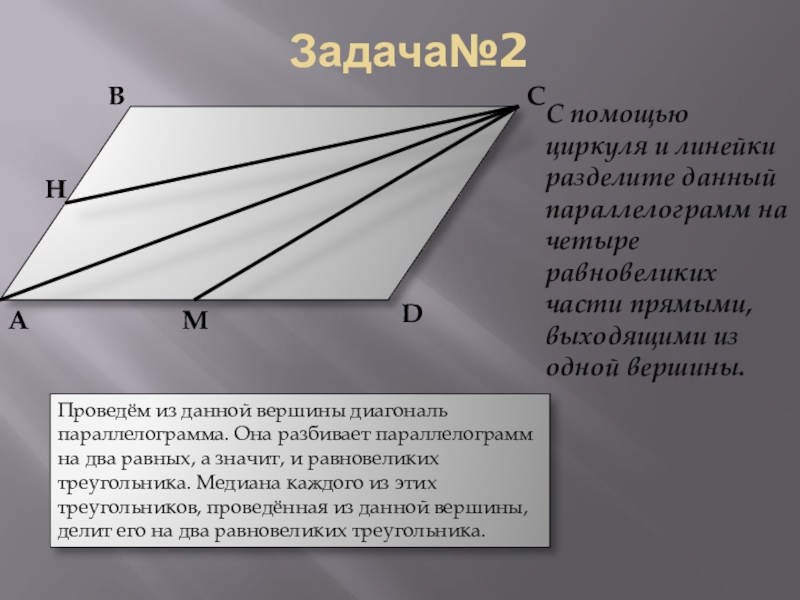
С помощью циркуля и линейки разделите данный параллелограмм на четыре равновеликих
Проведём из данной вершины диагональ параллелограмма. Она разбивает параллелограмм на два равных, а значит, и равновеликих треугольника. Медиана каждого из этих треугольников, проведённая из данной вершины, делит его на два равновеликих треугольника.
A
B
С
D
H
M
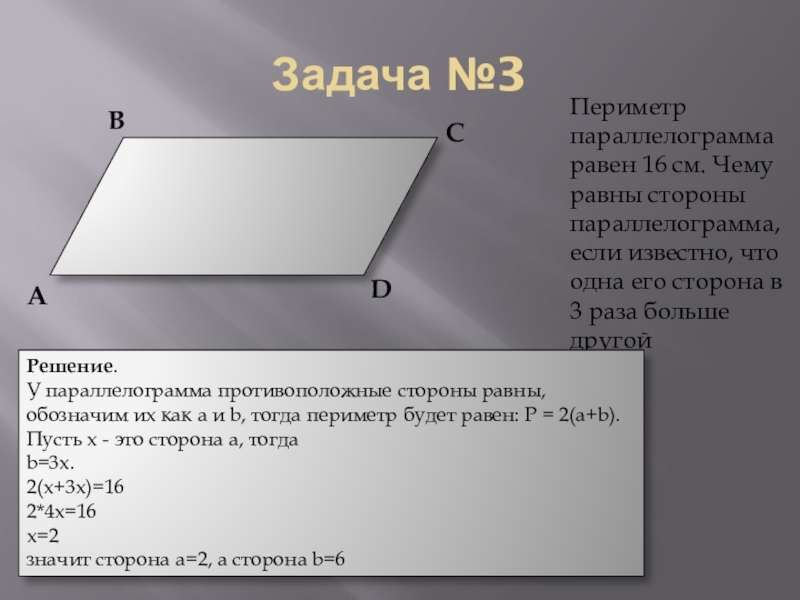
Слайд 22Задача №3
Периметр параллелограмма равен 16 см. Чему равны стороны параллелограмма, если
A
B
С
D
Решение.
У параллелограмма противоположные стороны равны, обозначим их как а и b, тогда периметр будет равен: Р = 2(а+b).
Пусть х - это сторона а, тогда
b=3х.
2(х+3х)=16
2*4х=16
х=2
значит сторона а=2, а сторона b=6
Слайд 23Задача №4
В параллелограмме ABCD диагональ BD = 6 см и образует
Решение.
Поскольку нам дана величина угла ADB (диагональ параллелограмма образует со сторонами AD и DC углы по 60 градусов), то величина угла DBC также равна 60 градусов, поскольку противоположные стороны параллелограмма параллельны, соответственно диагональ является секущей для двух параллельных прямых AD и BC, а для любой секущей внутренние накрест лежащие углы равны.
Таким образом, в треугольнике BCD нам известны два угла из трех, и они оба равны 60 градусов. Соответственно, поскольку сумма углов треугольника равна 180 градусов, то угол BCD также равен 60 градусам, из чего следует, что треугольник BCD - равносторонний.
Поскольку треугольник BCD - равносторонний, то BC = CD = BD = 6 см.
Таким образом, поскольку противолежащие стороны параллелограмма равны, периметр его равен 24 см. Параллелограмм является ромбом.
Дополнительно:
Поскольку точка М лежит на стороне CD, то AB и MD - параллельны, следовательно, ABMD - трапеция.
Угол DAB трапеции равен 60 градусов, исходя из решения, изложенного выше, как угол параллелограмма.
Угол ADM равен 120 градусов, так как по условию диагональ BD образует со сторонами AD и DC углы по 60 градусов, а ADM равен сумме данных углов.
Поскольку по условию точка M - середина DC, CM = MD. Значит BM - медиана треугольника DBC. Как указано выше, треугольник DBC - равносторонний, а в равностороннем треугольнике медиана является, одновременно, биссектрисой и высотой. Значит, угол DBM равен половине угла DBC и равен 60 / 2 = 30 градусов. Откуда угол ABM = 60 + 30 = 90 градусов. Поскольку BM - высота, то BMD равен также 90 градусов.
Исходя из сказанного, ABMD - прямоугольная трапеция.
Ответ: 24 см. 60º, 90º, 90º, 120º - прямоугольная трапеция.