- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Параллелограмм
Содержание
- 1. Параллелограмм
- 2. Задача №1 Найдите площадь параллелограмма, если две
- 3. Задача №2Периметр параллелограмма равен 46. Одна сторона
- 4. Задача №3Боковая сторона равнобедренного треугольника равна 10.
- 5. Задача №4Площадь параллелограмма равна 189. Точка Е— середина
- 6. Задача №5Площадь параллелограмма АВСD равна 153. Найдите площадь
- 7. Задача №6Площадь параллелограмма АВСD равна 176. Точка Е— середина
- 8. Задача №7В параллелограмме АВСD отмечена точка М— середина
- 9. Задача №8 Площадь параллелограмма равна
- 10. Задача №9Точка пересечения биссектрис двух углов параллелограмма,
- 11. Задача №10В параллелограмме АВСD высота, опущенная на сторону АВ, равна 4, АD=8. Найдите синус угла B.
- 12. Задача №11В параллелограмме АВСD высота, опущенная на сторону АВ, равна 4, sinA = 2/3. Найдите АD.
- 13. Задача №12В параллелограмме АВСD sinС = 3/7,
- 14. Задача №13В параллелограмме АВСD АВ=3, АD=21, sinА
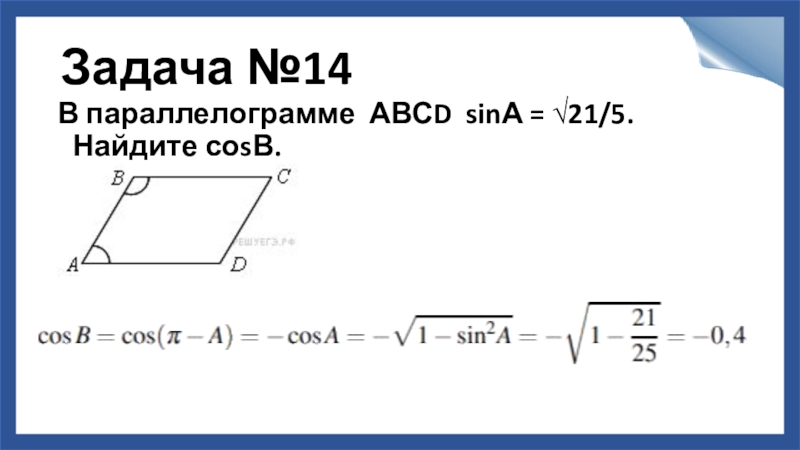
- 15. Задача №14В параллелограмме АВСD sinА = √21/5. Найдите соsВ.
- 16. Задача №15Параллелограмм и прямоугольник имеют одинаковые стороны.
- 17. Задача №16Найдите угол между биссектрисами углов параллелограмма,
- 18. Задача №17Биссектриса тупого угла параллелограмма делит противоположную
- 19. Задача №18 В параллелограмме АВСD диагональ AC
Слайд 2Задача №1
Найдите площадь параллелограмма, если две его стороны равны 8
Площадь параллелограмма равна произведению
его сторон на синус угла между ними.
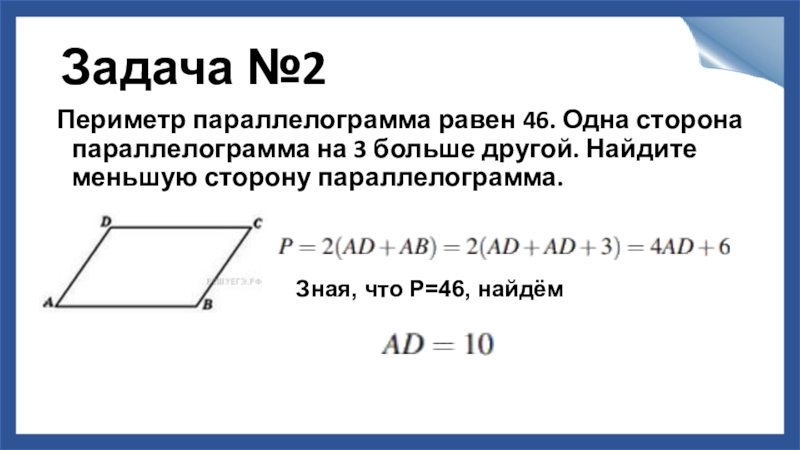
Слайд 3Задача №2
Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше
Зная, что Р=46, найдём
Слайд 4Задача №3
Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на
Т.к. прямые, проведенные из основания треугольника АВС параллельны его сторонам, то углы в треугольниках AFD и BDE равны углам треугольника ABC. Треугольники подобны, значит, они тоже равнобедренные. Противоположные стороны параллелограмма попарно равны, значит
Слайд 5Задача №4
Площадь параллелограмма равна 189. Точка Е— середина стороны АD. Найдите площадь
Площадь трапеции равна полусумме оснований, умноженной на высоту. Выразим площадь трапеции через площадь параллелограмма:
Слайд 6Задача №5
Площадь параллелограмма АВСD равна 153. Найдите площадь параллелограмма А´В´С´D´, вершинами которого
Четырехугольник, вершинами которого являются середины сторон произвольного четырехугольника, является параллелограммом, площадь которого равна половине площади исходного четырехугольника
Ответ:76,5.
Слайд 7Задача №6
Площадь параллелограмма АВСD равна 176. Точка Е— середина стороны СD. Найдите площадь
Выразим площадь треугольника АDЕ
через площадь параллелограмма АВСD
Слайд 8Задача №7
В параллелограмме АВСD отмечена точка М— середина стороны ВС. Отрезки АМ и ВD
Обозначим О точку пересечения диагоналей параллелограмма. Диагонали параллелограмма точкой пересечения делятся пополам, поэтому ВО — медиана треугольника АВС. Отрезок АМ также является медианой треугольника АВС, точкой пересечения К медианы делятся в отношении 2:1, считая от вершины.
Поэтому ВК=(ВD:2)·2/3= 4
О
Слайд 9Задача №8
Площадь параллелограмма равна 40, две его стороны равны
Т.к. площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание.
Пусть высоты равны соответственно a и b. Тогда S=5·a=10·b=40. Поэтому a = 8, b = 4. Большая высота равна 8.
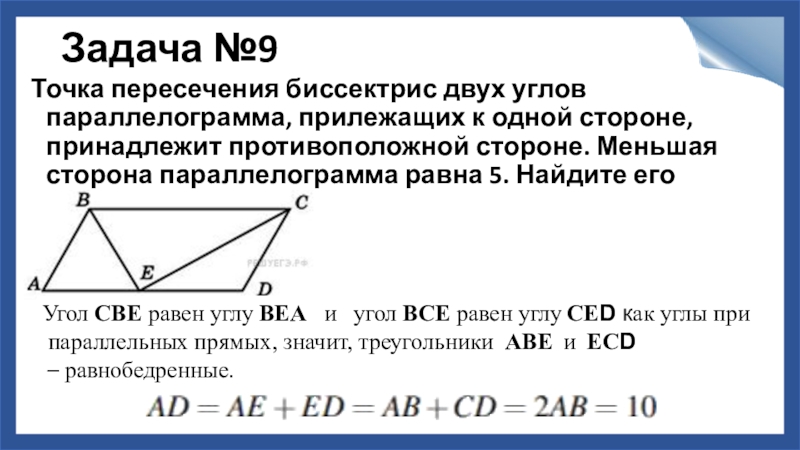
Слайд 10Задача №9
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне,
Угол СВЕ равен углу ВЕА и угол ВСЕ равен углу СЕD как углы при
параллельных прямых, значит, треугольники АВЕ и ЕСD
– равнобедренные.
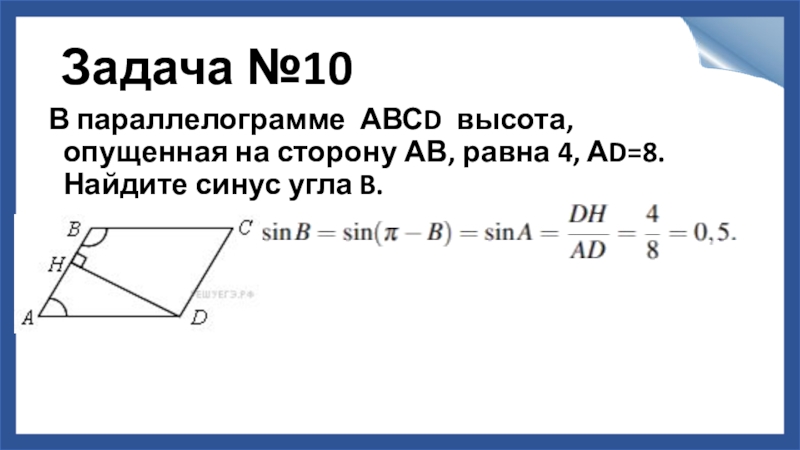
Слайд 11Задача №10
В параллелограмме АВСD высота, опущенная на сторону АВ, равна 4, АD=8.
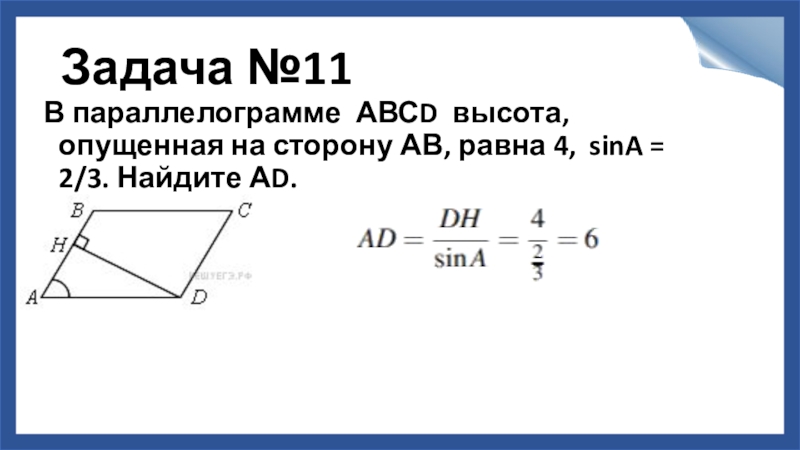
Слайд 12Задача №11
В параллелограмме АВСD высота, опущенная на сторону АВ, равна 4, sinA
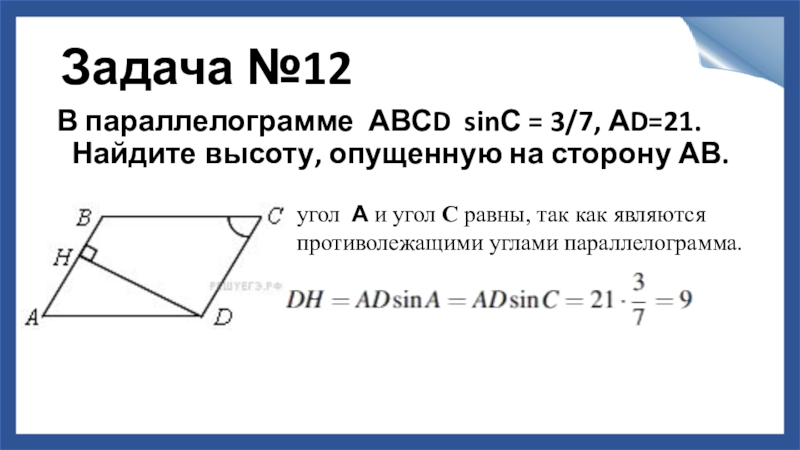
Слайд 13Задача №12
В параллелограмме АВСD sinС = 3/7, АD=21.Найдите высоту, опущенную на
угол А и угол С равны, так как являются
противолежащими углами параллелограмма.
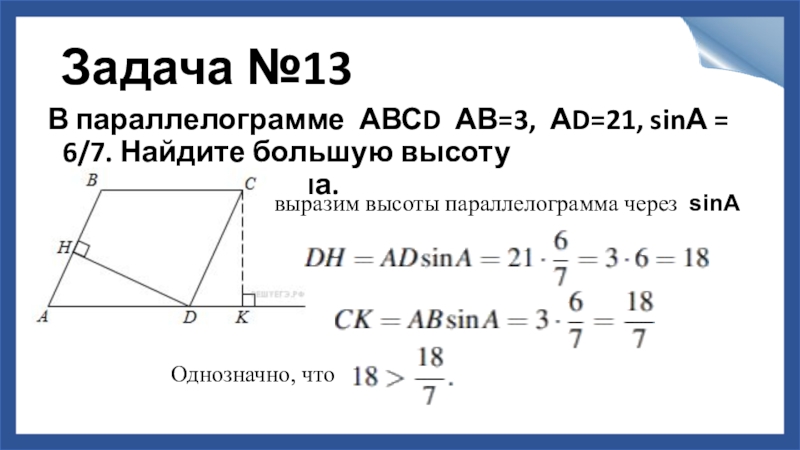
Слайд 14Задача №13
В параллелограмме АВСD АВ=3, АD=21, sinА = 6/7. Найдите большую
выразим высоты параллелограмма через sinА
Однозначно, что
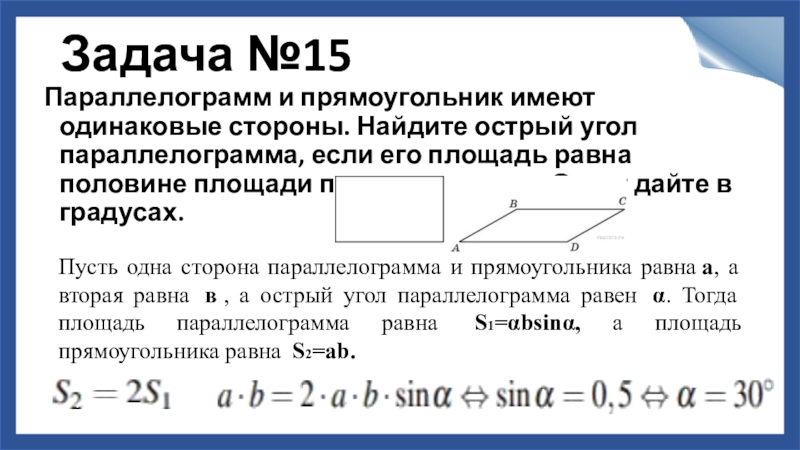
Слайд 16Задача №15
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма,
Пусть одна сторона параллелограмма и прямоугольника равна а, а вторая равна в , а острый угол параллелограмма равен α. Тогда площадь параллелограмма равна S1=αbsinα, а площадь прямоугольника равна S2=ab.
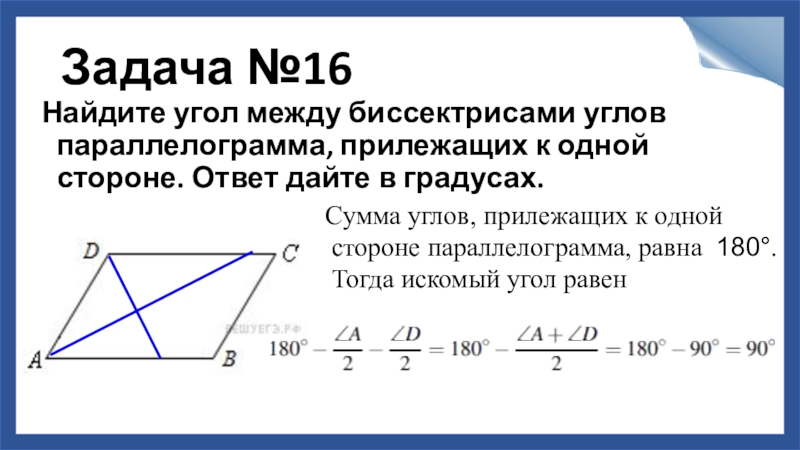
Слайд 17Задача №16
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне.
Cумма углов, прилежащих к одной
стороне параллелограмма, равна 180°.
Тогда искомый угол равен
Слайд 18Задача №17
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3,
Заметим, что угол СDL = ALD как накрест лежащие углы при пересечении параллельных прямых секущей. Значит, треугольник ADL – равнобедренный. Пусть AL=4x, тогда AD=4x, AB=7x. Противоположные стороны параллелограмма АВСD попарно равны, тогда
x=4
AB=7x=28
Слайд 19Задача №18
В параллелограмме АВСD диагональ AC в два раза больше стороны AB
o
Dдиагонали параллелограмма делятся точкой пересечения пополам, значит:
ΔCOD — равнобедренный, ∟COD=∟CDO. Сумма углов треугольника равна 180°: