Презентация, доклад на тему Параллельные прямые в пространстве

Содержание

1. Параллельные прямые в пространстве
2. Параллельные прямые в пространстве1Что такое стереометрия?Стереометрия – это раздел геометрии, в котором изучают тела в пространстве.
3. Параллельные прямые в пространстве2Сформулируйте три основные аксиомы
4. Параллельные прямые в пространстве3Сформулируйте теорему о существовании
5. Параллельные прямые в пространстве4Сформулируйте теорему о существовании
6. Параллельные прямые в пространстве6Каково может быть взаимное расположение двух прямых на плоскости?совпадают, пересекаются, параллельны.
7. Параллельные прямые в пространстве7Сформулируйте аксиому и следствия
8. Параллельные прямые в пространствеПараллельными прямыми в пространстве
9. αавПараллельные прямые в пространстве
10. Параллельные прямые в пространствеДан куб. Являются ли
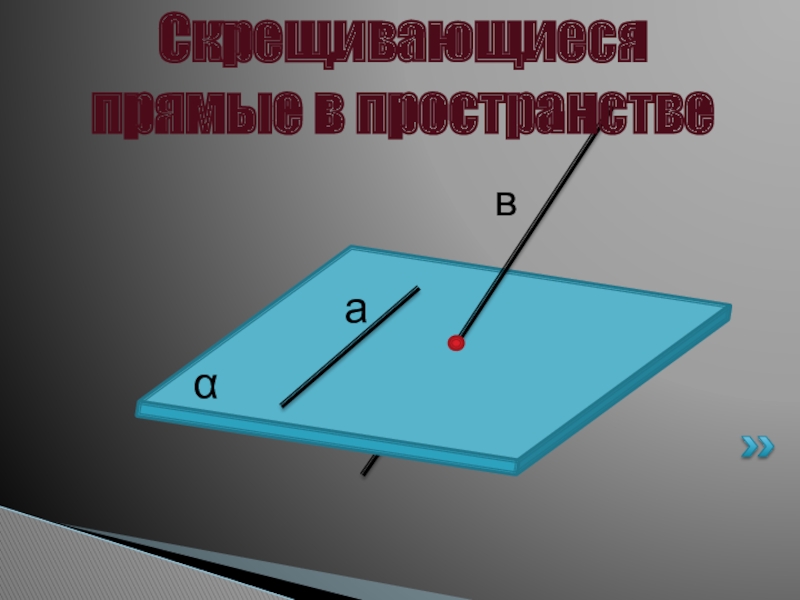
11. Параллельные прямые в пространствеДве прямые называются скрещивающимися, если они не лежат в одной плоскости.
12. αавСкрещивающиеся прямые в пространстве
13. Параллельные прямые в пространстве9По рисункам назовите:1) пары скрещивающихся ребер;2) пары параллельных ребер.ABKLNK1L1N1
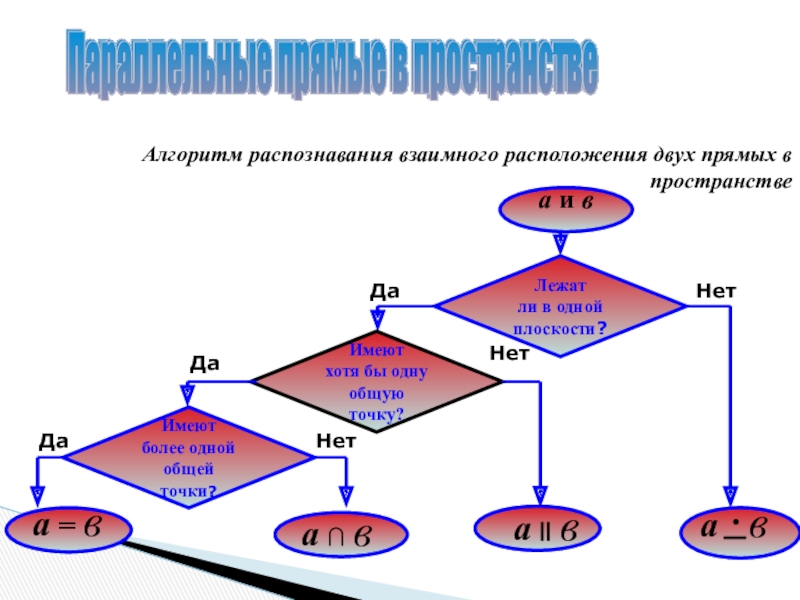
14. Параллельные прямые в пространствеАлгоритм распознавания взаимного расположения двух прямых в пространствеа и вДаДаДаНетНетНетПараллельные прямые в пространстве
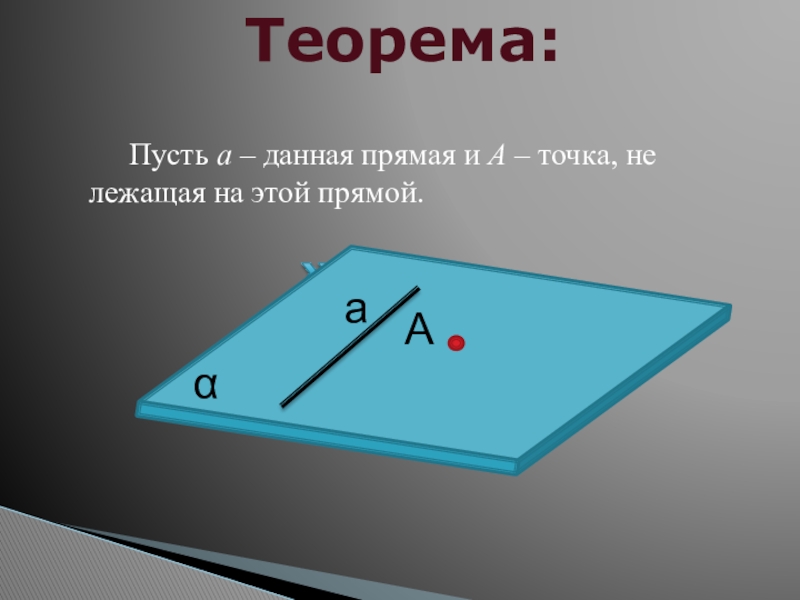
15. Параллельные прямые в пространствеТеорема: Через точку вне
16. αаТеорема:А Пусть а – данная прямая и А – точка, не лежащая на этой прямой.
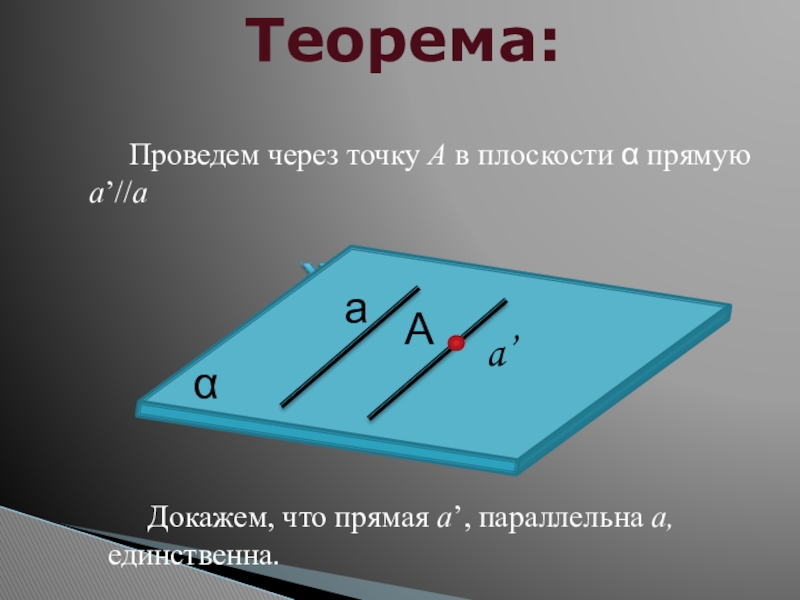
17. αаa’Теорема:А Проведем через точку А в плоскости α прямую а’//а Докажем, что прямая а’, параллельна а, единственна.
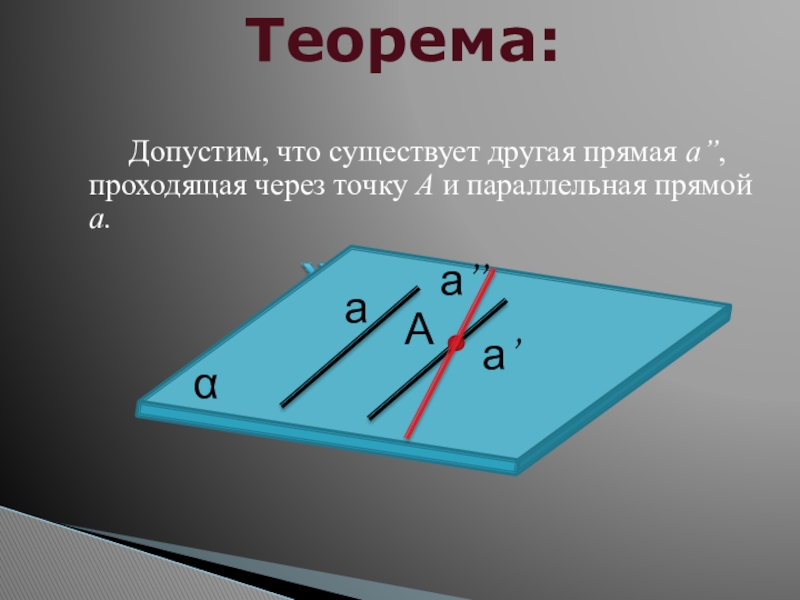
18. αаа’Теорема:А Допустим, что существует другая прямая а’’, проходящая через точку А и параллельная прямой а.а’’
19. αавТеорема:А Через прямые а и а’’ можно провести
20. Параллельные прямые в пространстве10Всегда ли две непересекающиеся
21. Параллельные прямые в пространствеДомашнее задание.§2, п. 7, № 2.
22. Параллельные прямые в пространствеСпасибо за урок! До свидания!

Параллельные прямые в пространстве1Что такое стереометрия?Стереометрия – это раздел геометрии, в котором изучают тела в пространстве.

Главная
Геометрия
Параллельные прямые в пространстве

Слайд 1Параллельные прямые
в пространстве

Слайд 2Параллельные прямые в пространстве
1
Что такое стереометрия?

Стереометрия – это раздел геометрии, в

котором изучают тела в пространстве.

Слайд 3Параллельные прямые в пространстве
2
Сформулируйте три основные аксиомы стереометрии.
I аксиома: Какова бы

ни была плоскость, существуют точки принадлежащие этой плоскости, и тоски, не принадлежащие ей.

II аксиома: Если две различные плоскости имеют общую точку, то они пересекаются по прямой, содержащую эту точку.

III аксиома: Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

Параллельные прямые в пространстве2Сформулируйте три основные аксиомы стереометрии.I аксиома: Какова бы ни была плоскость, существуют точки принадлежащие

Слайд 4Параллельные прямые в пространстве
3
Сформулируйте теорему о существовании плоскости, проходящей через данную

прямую и данную точку.

Теорема: Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

Слайд 5Параллельные прямые в пространстве
4
Сформулируйте теорему о существовании плоскости, проходящей через три

точки.

Теорема: Через три точки не лежащие на одной прямой, можно провести плоскость и притом только одну.

Слайд 6Параллельные прямые в пространстве
6
Каково может быть взаимное расположение двух прямых на

плоскости?

совпадают,
пересекаются,
параллельны.

Слайд 7Параллельные прямые в пространстве
7
Сформулируйте аксиому и следствия параллельных прямых.
1.Через точку, не

лежащую на данной прямой, Через точку, не лежащую на данной прямой,

2. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

3. Если две прямые параллельны третьей прямой, то они параллельны.

Параллельные прямые в пространстве7Сформулируйте аксиому и следствия параллельных прямых.1.Через точку, не лежащую на данной прямой, Через точку,

Слайд 8Параллельные прямые в пространстве
Параллельными прямыми в пространстве называются прямые, лежащие в

одной плоскости и не пересекающие друг друга.

Параллельные прямые в пространстве

Слайд 9α
а
в
Параллельные прямые в пространстве

Слайд 10Параллельные прямые в пространстве
Дан куб. Являются ли параллельными прямые:
D
C
A
B
D1
C1
A1
B1
1) АА1 и

DD1, АА1 и СС1? Ответ обоснуйте.

2) АА1 и DС? Они пересекаются?

В пространстве есть прямые, которые не пересекаются, но и не являются параллельными.

Параллельные прямые в пространствеДан куб. Являются ли параллельными прямые:DCABD1C1A1B11) АА1 и DD1, АА1 и СС1? Ответ обоснуйте.2)

Слайд 11Параллельные прямые в пространстве
Две прямые называются скрещивающимися, если они не лежат

в одной плоскости.

Слайд 12α
а
в
Скрещивающиеся прямые в пространстве

Слайд 13Параллельные прямые в пространстве
9
По рисункам назовите:
1) пары скрещивающихся ребер;
2) пары параллельных

ребер.

Слайд 14Параллельные прямые в пространстве
Алгоритм распознавания взаимного расположения двух прямых в пространстве
а

и в

Да

Нет

Параллельные прямые в пространстве

Слайд 15Параллельные прямые в пространстве
Теорема: Через точку вне данной прямой можно провести

прямую, параллельную этой прямой и притом только одну.

Параллельные прямые в пространствеТеорема: Через точку вне данной прямой можно провести прямую, параллельную этой прямой и притом

Слайд 16α
а
Теорема:
А
Пусть а – данная прямая и А – точка, не лежащая

на этой прямой.

Слайд 17α
а
a’
Теорема:
А
Проведем через точку А в плоскости α прямую а’//а
Докажем, что прямая

а’, параллельна а, единственна.

Слайд 18α
а
а’
Теорема:
А
Допустим, что существует другая прямая а’’, проходящая через точку А и

параллельная прямой а.

а’’

Слайд 19α
а
в
Теорема:
А
Через прямые а и а’’ можно провести плоскость α’. Плоскость α’

проходит через прямую а и точку А;

=>α=α’ (по теореме 1.1) => а’ =а’’(по аксиоме параллельных прямых). Что и требовалось доказать.

αавТеорема:А Через прямые а и а’’ можно провести плоскость α’. Плоскость α’ проходит через прямую а и точку

Слайд 20Параллельные прямые в пространстве
10
Всегда ли две непересекающиеся прямые в пространстве параллельны?
11
Какие

две прямые в пространстве называются параллельными?

Дано: а // в . Докажите, что все прямые, пересекающие данные лежат в одной плоскости.

Сколько можно провести в пространстве прямых, проходящих через данную точку, параллельных данной прямой?

Параллельные прямые в пространстве10Всегда ли две непересекающиеся прямые в пространстве параллельны?11Какие две прямые в пространстве называются параллельными?12Дано:

Слайд 21Параллельные прямые в пространстве
Домашнее задание.
§2, п. 7, № 2.

Слайд 22Параллельные прямые в пространстве
Спасибо за урок!
До свидания!

Скачать презентацию

Презентация, доклад на тему Параллельные прямые в пространстве

Содержание

Слайд 1Параллельные прямые
в пространстве

Слайд 2Параллельные прямые в пространстве
1
Что такое стереометрия?

Стереометрия – это раздел геометрии, в

Слайд 3Параллельные прямые в пространстве
2
Сформулируйте три основные аксиомы стереометрии.
I аксиома: Какова бы

Слайд 4Параллельные прямые в пространстве
3
Сформулируйте теорему о существовании плоскости, проходящей через данную

Слайд 5Параллельные прямые в пространстве
4
Сформулируйте теорему о существовании плоскости, проходящей через три

Слайд 6Параллельные прямые в пространстве
6
Каково может быть взаимное расположение двух прямых на

Слайд 7Параллельные прямые в пространстве
7
Сформулируйте аксиому и следствия параллельных прямых.
1.Через точку, не

Слайд 8Параллельные прямые в пространстве
Параллельными прямыми в пространстве называются прямые, лежащие в

Слайд 9α
а
в
Параллельные прямые в пространстве

Слайд 10Параллельные прямые в пространстве
Дан куб. Являются ли параллельными прямые:
D
C
A
B
D1
C1
A1
B1
1) АА1 и

Слайд 11Параллельные прямые в пространстве
Две прямые называются скрещивающимися, если они не лежат

Слайд 12α
а
в
Скрещивающиеся прямые в пространстве

Слайд 13Параллельные прямые в пространстве
9
По рисункам назовите:
1) пары скрещивающихся ребер;
2) пары параллельных

Слайд 14Параллельные прямые в пространстве
Алгоритм распознавания взаимного расположения двух прямых в пространстве
а

Слайд 15Параллельные прямые в пространстве
Теорема: Через точку вне данной прямой можно провести

Слайд 16α
а
Теорема:
А
Пусть а – данная прямая и А – точка, не лежащая

Слайд 17α
а
a’
Теорема:
А
Проведем через точку А в плоскости α прямую а’//а
Докажем, что прямая

Слайд 18α
а
а’
Теорема:
А
Допустим, что существует другая прямая а’’, проходящая через точку А и

Слайд 19α
а
в
Теорема:
А
Через прямые а и а’’ можно провести плоскость α’. Плоскость α’

Слайд 20Параллельные прямые в пространстве
10
Всегда ли две непересекающиеся прямые в пространстве параллельны?
11
Какие

Слайд 21Параллельные прямые в пространстве
Домашнее задание.
§2, п. 7, № 2.

Слайд 22Параллельные прямые в пространстве
Спасибо за урок!
До свидания!

Что такое shareslide.ru?

Обратная связь

Презентация, доклад на тему Параллельные прямые в пространстве

Содержание

Слайд 1Параллельные прямыев пространстве

Слайд 2Параллельные прямые в пространстве1Что такое стереометрия?Стереометрия – это раздел геометрии, в

Слайд 3Параллельные прямые в пространстве2Сформулируйте три основные аксиомы стереометрии.I аксиома: Какова бы

Слайд 4Параллельные прямые в пространстве3Сформулируйте теорему о существовании плоскости, проходящей через данную

Слайд 5Параллельные прямые в пространстве4Сформулируйте теорему о существовании плоскости, проходящей через три

Слайд 6Параллельные прямые в пространстве6Каково может быть взаимное расположение двух прямых на

Слайд 7Параллельные прямые в пространстве7Сформулируйте аксиому и следствия параллельных прямых.1.Через точку, не

Слайд 8Параллельные прямые в пространствеПараллельными прямыми в пространстве называются прямые, лежащие в

Слайд 9αавПараллельные прямые в пространстве

Слайд 10Параллельные прямые в пространствеДан куб. Являются ли параллельными прямые:DCABD1C1A1B11) АА1 и

Слайд 11Параллельные прямые в пространствеДве прямые называются скрещивающимися, если они не лежат

Слайд 12αавСкрещивающиеся прямые в пространстве

Слайд 13Параллельные прямые в пространстве9По рисункам назовите:1) пары скрещивающихся ребер;2) пары параллельных

Слайд 14Параллельные прямые в пространствеАлгоритм распознавания взаимного расположения двух прямых в пространствеа

Слайд 15Параллельные прямые в пространствеТеорема: Через точку вне данной прямой можно провести

Слайд 16αаТеорема:А Пусть а – данная прямая и А – точка, не лежащая

Слайд 17αаa’Теорема:А Проведем через точку А в плоскости α прямую а’//а Докажем, что прямая

Слайд 18αаа’Теорема:А Допустим, что существует другая прямая а’’, проходящая через точку А и

Слайд 19αавТеорема:А Через прямые а и а’’ можно провести плоскость α’. Плоскость α’

Слайд 20Параллельные прямые в пространстве10Всегда ли две непересекающиеся прямые в пространстве параллельны?11Какие

Слайд 21Параллельные прямые в пространствеДомашнее задание.§2, п. 7, № 2.

Слайд 22Параллельные прямые в пространствеСпасибо за урок! До свидания!

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 1Параллельные прямые
в пространстве

Слайд 2Параллельные прямые в пространстве
1
Что такое стереометрия?

Стереометрия – это раздел геометрии, в

Слайд 3Параллельные прямые в пространстве
2
Сформулируйте три основные аксиомы стереометрии.
I аксиома: Какова бы

Слайд 4Параллельные прямые в пространстве
3
Сформулируйте теорему о существовании плоскости, проходящей через данную

Слайд 5Параллельные прямые в пространстве
4
Сформулируйте теорему о существовании плоскости, проходящей через три

Слайд 6Параллельные прямые в пространстве
6
Каково может быть взаимное расположение двух прямых на

Слайд 7Параллельные прямые в пространстве
7
Сформулируйте аксиому и следствия параллельных прямых.
1.Через точку, не

Слайд 8Параллельные прямые в пространстве
Параллельными прямыми в пространстве называются прямые, лежащие в

Слайд 9α
а
в
Параллельные прямые в пространстве

Слайд 10Параллельные прямые в пространстве
Дан куб. Являются ли параллельными прямые:
D
C
A
B
D1
C1
A1
B1
1) АА1 и

Слайд 11Параллельные прямые в пространстве
Две прямые называются скрещивающимися, если они не лежат

Слайд 12α
а
в
Скрещивающиеся прямые в пространстве

Слайд 13Параллельные прямые в пространстве
9
По рисункам назовите:
1) пары скрещивающихся ребер;
2) пары параллельных

Слайд 14Параллельные прямые в пространстве
Алгоритм распознавания взаимного расположения двух прямых в пространстве
а

Слайд 15Параллельные прямые в пространстве
Теорема: Через точку вне данной прямой можно провести

Слайд 16α
а
Теорема:
А
Пусть а – данная прямая и А – точка, не лежащая

Слайд 17α
а
a’
Теорема:
А
Проведем через точку А в плоскости α прямую а’//а
Докажем, что прямая

Слайд 18α
а
а’
Теорема:
А
Допустим, что существует другая прямая а’’, проходящая через точку А и

Слайд 19α
а
в
Теорема:
А
Через прямые а и а’’ можно провести плоскость α’. Плоскость α’

Слайд 20Параллельные прямые в пространстве
10
Всегда ли две непересекающиеся прямые в пространстве параллельны?
11
Какие

Слайд 21Параллельные прямые в пространстве
Домашнее задание.
§2, п. 7, № 2.

Слайд 22Параллельные прямые в пространстве
Спасибо за урок!
До свидания!