- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Параллельность в пространстве, презентация
Содержание
- 1. Параллельность в пространстве, презентация
- 2. Th1 Через точку вне данной прямой можно провести прямую, параллельную данной, и притом только одну.
- 3. Th2 Если одна из двух прямых лежит
- 4. Лемма Если одна из двух параллельных прямых пересекает плоскость, то и другая пересекает эту плоскость.
- 5. Th3 Две прямые, параллельные третьей, параллельны между собой. Другими словами, если
- 6. Теоремы Параллельность прямой и плоскости
- 7. Th4 Если прямая вне плоскости параллельна какой-нибудь
- 8. Теорема о следе. Если плоскость β проходит
- 9. Теоремы Параллельность плоскостей
- 10. Th6 Если плоскость α параллельна каждой из
- 11. Th7 Если две параллельные плоскости пересечены третьей,
- 12. Th8 Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну. OO1
- 13. Th9 Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны. АBА1B1
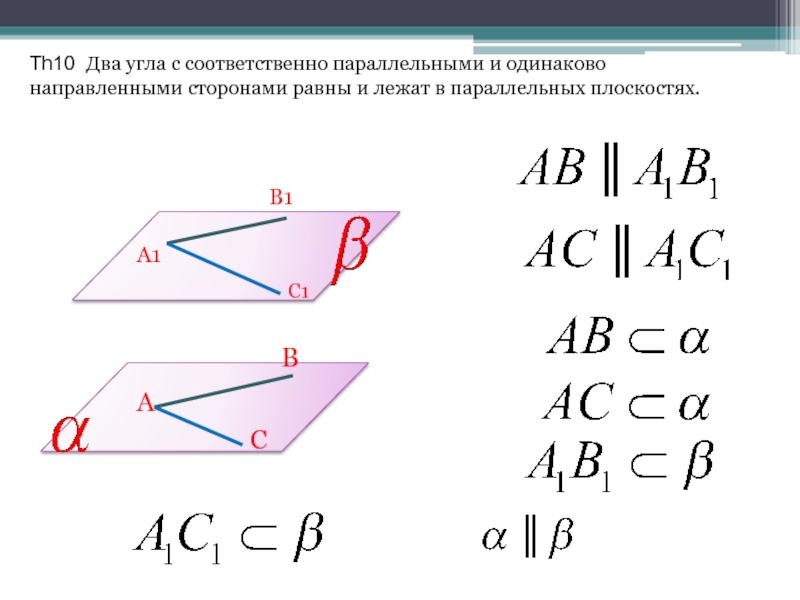
- 14. Th10 Два угла с соответственно параллельными и
- 15. Взаимное расположение прямых в пространстве
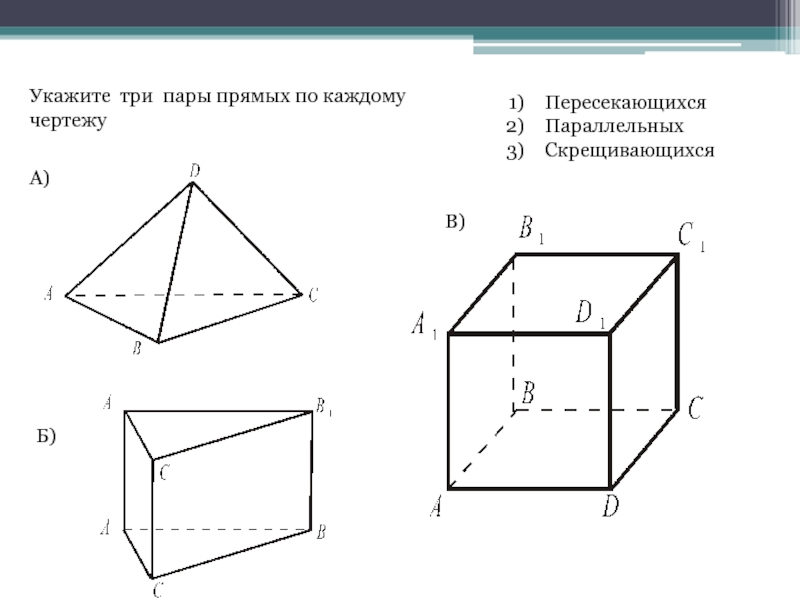
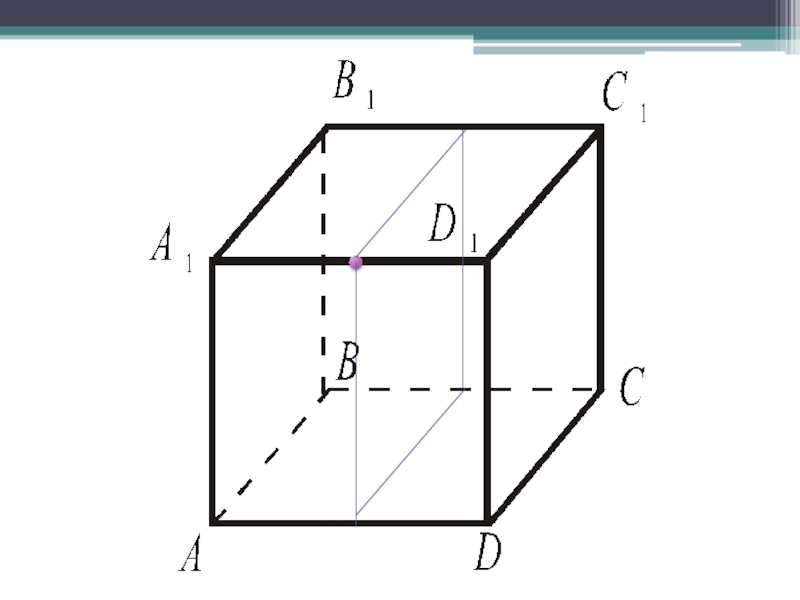
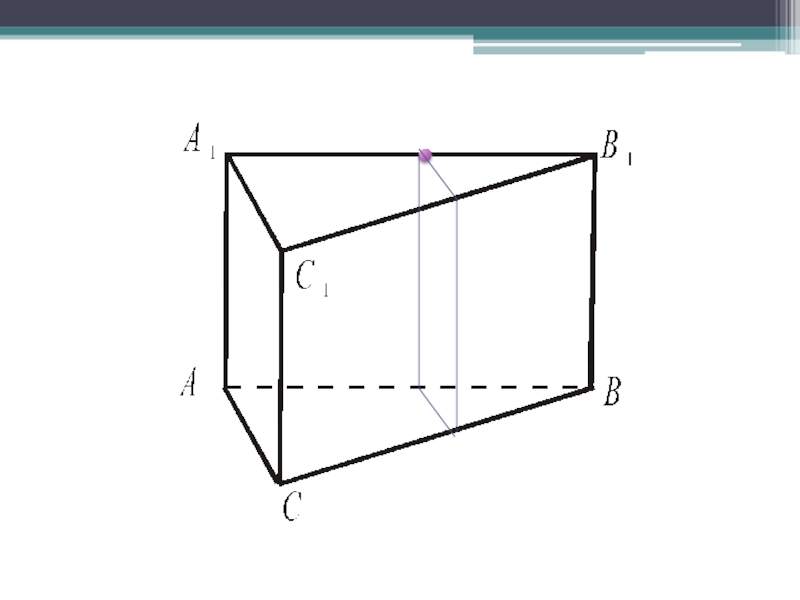
- 16. Укажите три пары прямых по каждому чертежу ПересекающихсяПараллельныхСкрещивающихсяА)Б)В)
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
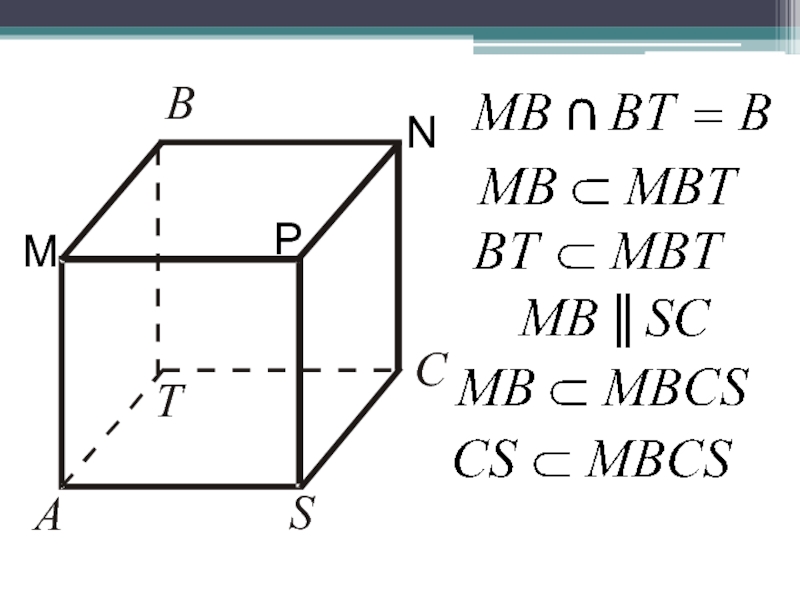
- 20. Укажите две пары прямых по каждому чертежу с использованием дополнительных точек. ПересекающихсяПараллельныхСкрещивающихсяА)Б)В)MMMPNNN
- 21. NPT
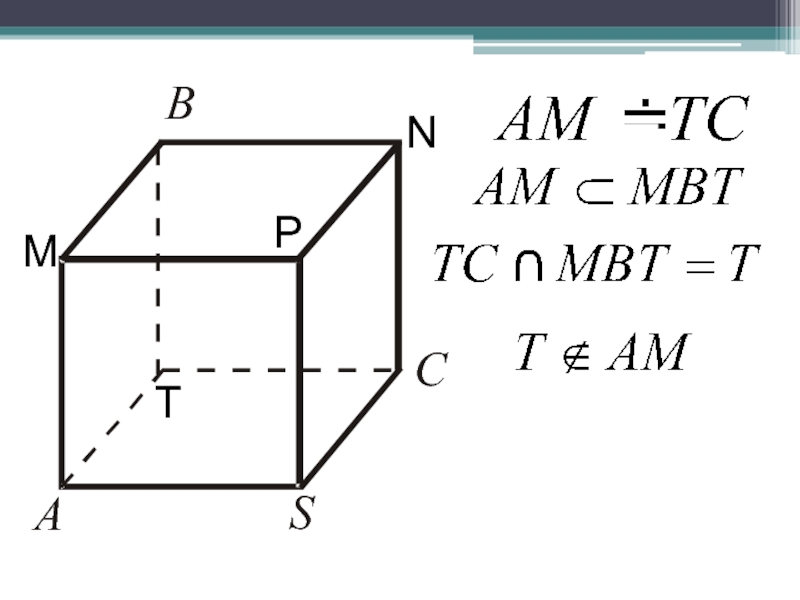
- 22. NPT
- 23. Теоремы Параллельность прямой и плоскости
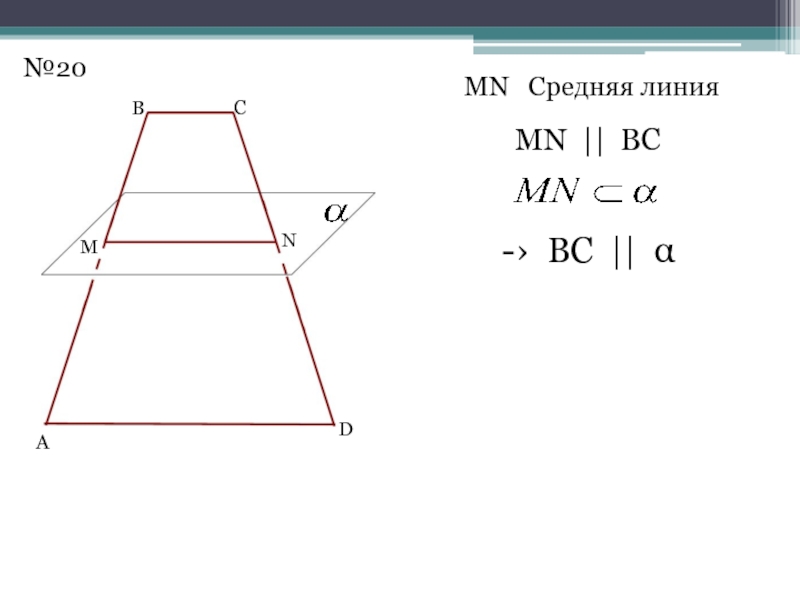
- 24. №20MN Средняя линияMN || ВС -› ВС || α ABCDMN
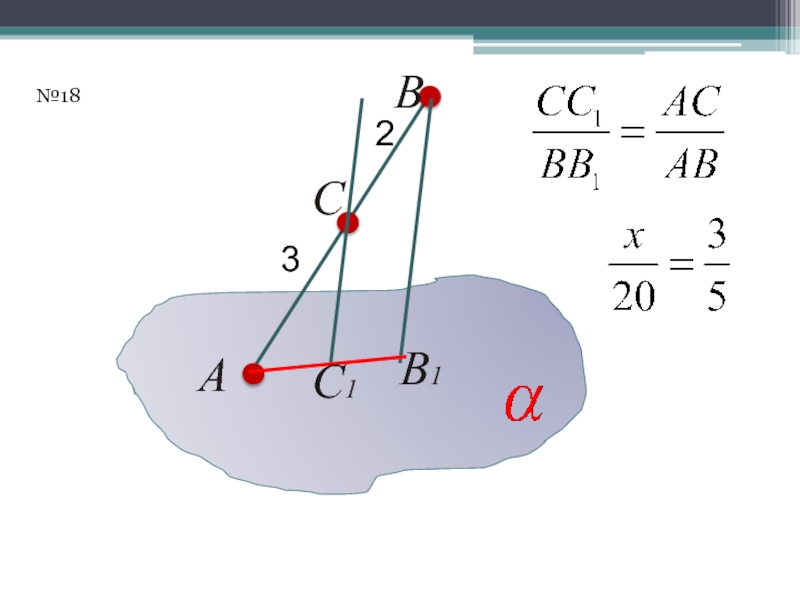
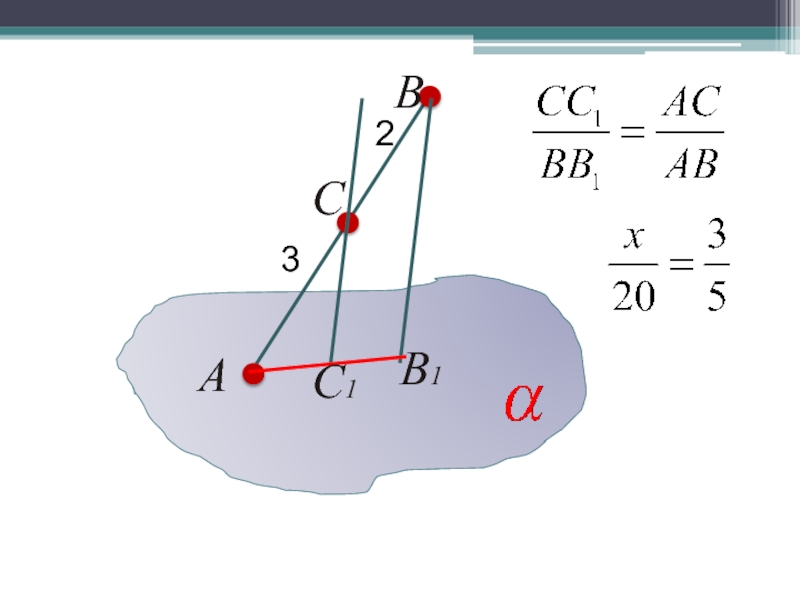
- 25. AВ1СС1В32№18
- 26. AВ1СС1В32
- 27. Слайд 27
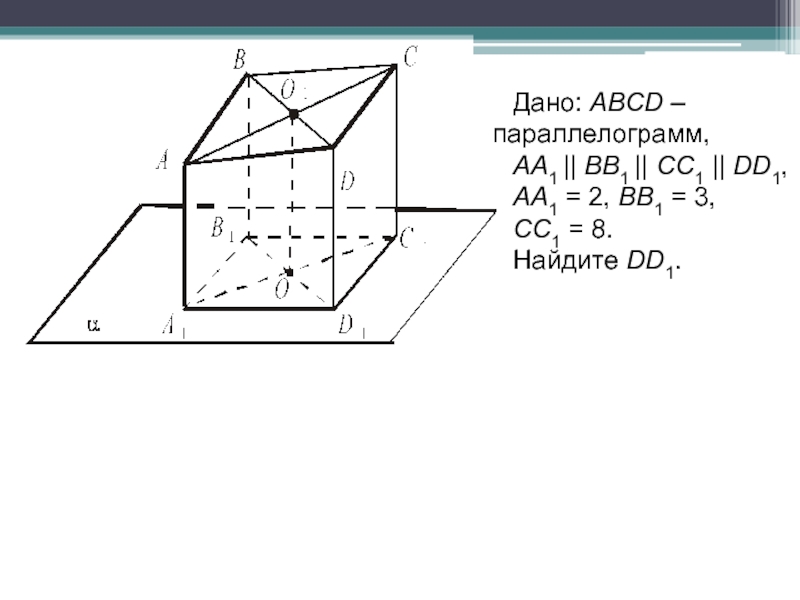
- 28. Дано: АВСD – параллелограмм,АА1 || ВВ1 ||
- 29. На рисунке точки Е и F лежат
- 30. № 54Дано: В (ADC), АМ =
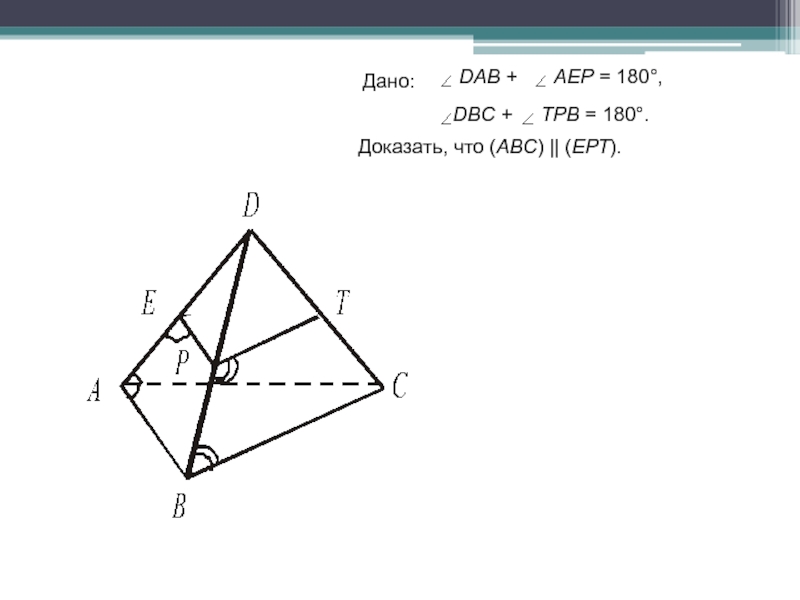
- 31. Дано: Доказать, что (АВС) || (ЕРТ). DAB +AEP = 180°,DBC +ТРВ = 180°.
- 32. Слайд 32
- 33. Слайд 33
Th1 Через точку вне данной прямой можно провести прямую, параллельную данной, и притом только одну.
Слайд 2Th1 Через точку вне данной прямой можно провести прямую, параллельную данной,
и притом только одну.
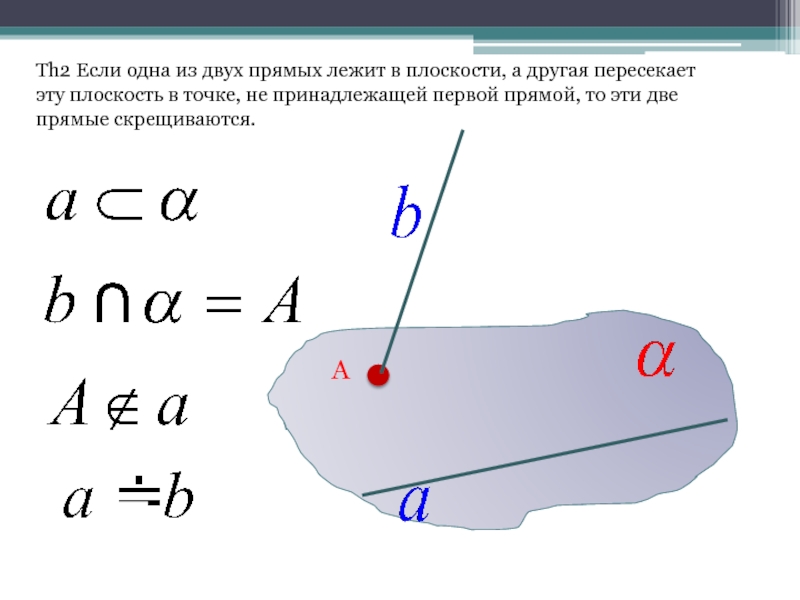
Слайд 3Th2 Если одна из двух прямых лежит в плоскости, а другая
пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти две прямые скрещиваются.
Слайд 4Лемма Если одна из двух параллельных прямых пересекает плоскость, то и
другая пересекает эту плоскость.
Слайд 7Th4 Если прямая вне плоскости параллельна какой-нибудь прямой на плоскости, то
эта прямая параллельна и самой плоскости.
Слайд 8Теорема о следе.
Если плоскость β проходит через прямую a, параллельную
плоскости α,
и пересекает эту плоскость по прямой b, то b || a.
и пересекает эту плоскость по прямой b, то b || a.
Слайд 10Th6 Если плоскость α параллельна каждой из двух пересекающихся прямых,
лежащих
в другой плоскости β, то эти плоскости параллельны.
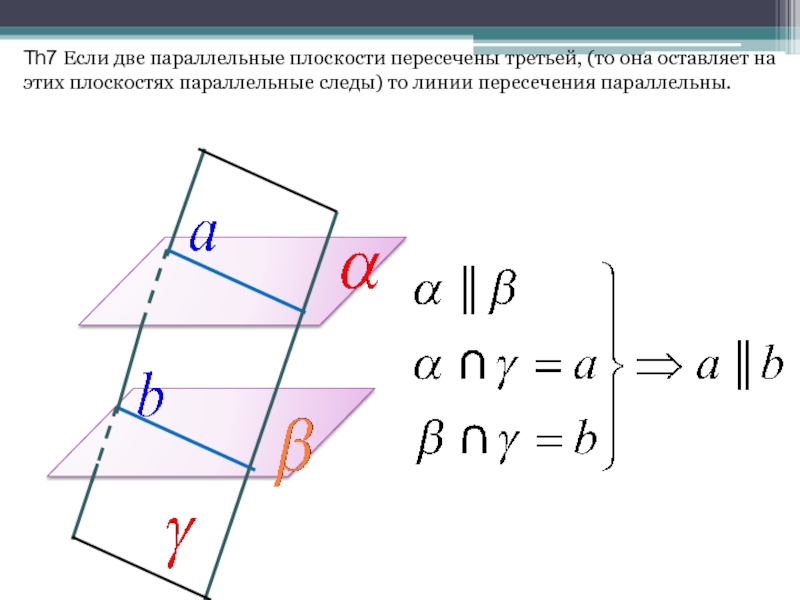
Слайд 11Th7 Если две параллельные плоскости пересечены третьей, (то она оставляет на
этих плоскостях параллельные следы) то линии пересечения параллельны.
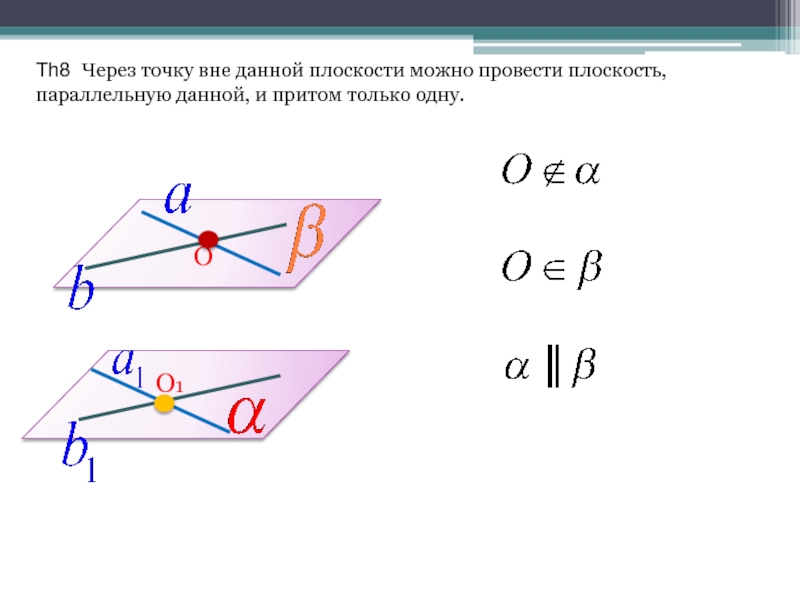
Слайд 12Th8 Через точку вне данной плоскости можно провести плоскость, параллельную данной,
и притом только одну.
O
O1
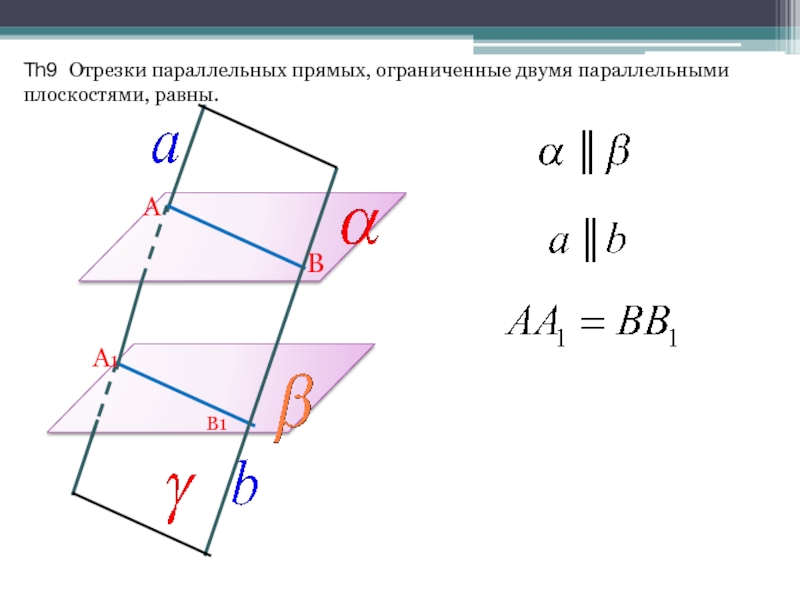
Слайд 13Th9 Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны.
А
B
А1
B1
Слайд 14Th10 Два угла с соответственно параллельными и одинаково направленными сторонами равны
и лежат в параллельных плоскостях.
B1
A
A1
C1
C
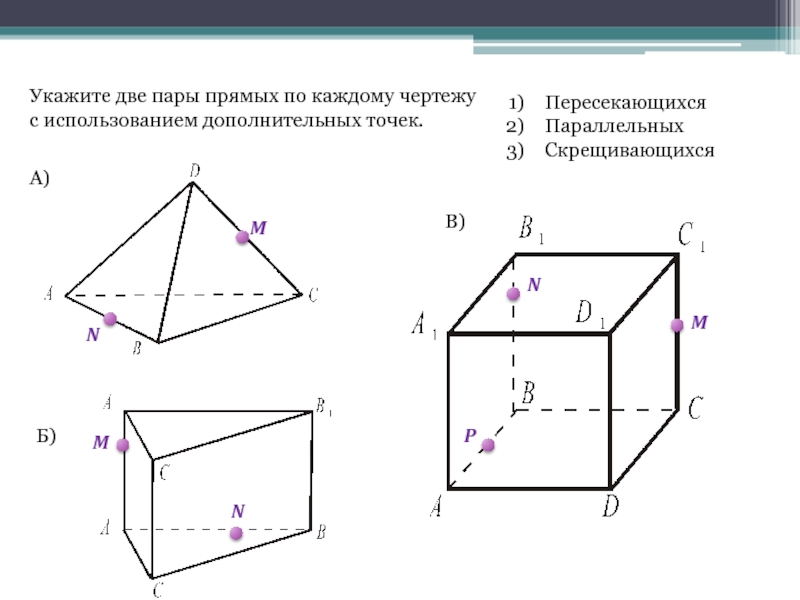
Слайд 20Укажите две пары прямых по каждому чертежу с использованием дополнительных точек.
Пересекающихся
Параллельных
Скрещивающихся
А)
Б)
В)
M
M
M
P
N
N
N
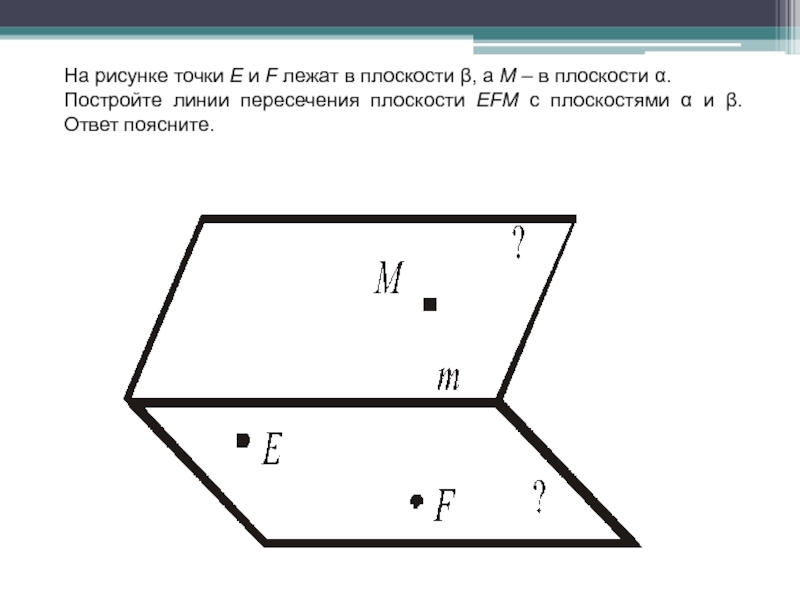
Слайд 29На рисунке точки Е и F лежат в плоскости β, а
М – в плоскости α.
Постройте линии пересечения плоскости EFM с плоскостями α и β.
Ответ поясните.
Постройте линии пересечения плоскости EFM с плоскостями α и β.
Ответ поясните.
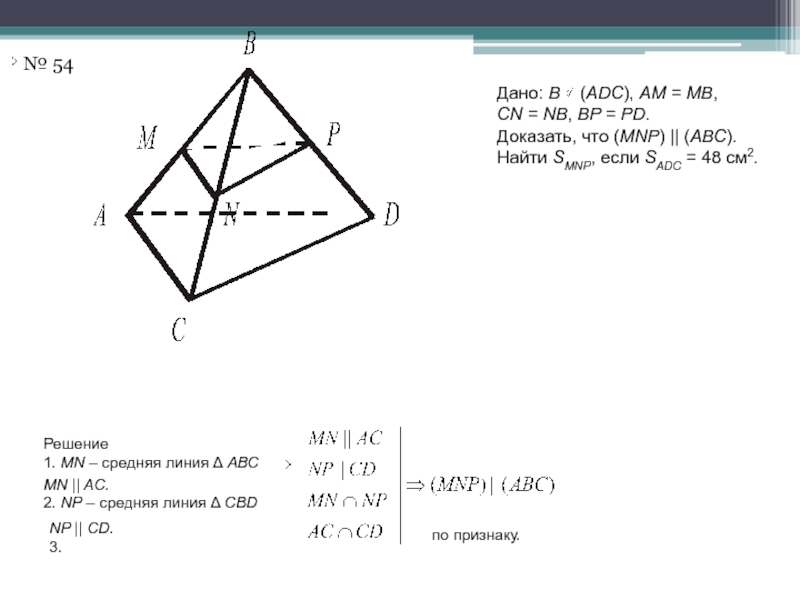
Слайд 30№ 54
Дано: В (ADC), АМ = МВ,
CN = NB, BP
= PD.
Доказать, что (MNP) || (АВС).
Найти SMNP, если SADC = 48 см2.
Доказать, что (MNP) || (АВС).
Найти SMNP, если SADC = 48 см2.