- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Основные способы решения задач планиметрии (9 класс)
Содержание
- 1. Основные способы решения задач планиметрии (9 класс)
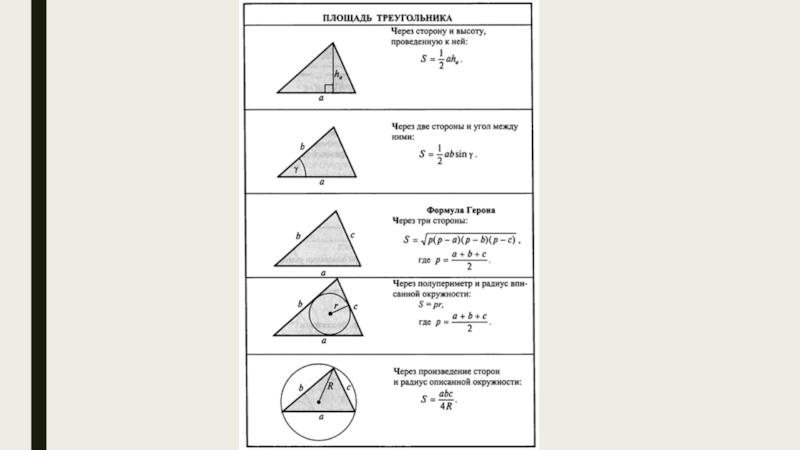
- 2. ПовторениеВспомним тему «Площадь треугольника». С помощью каких формул мы можем определить площадь треугольника?Ответ:
- 3. Слайд 3
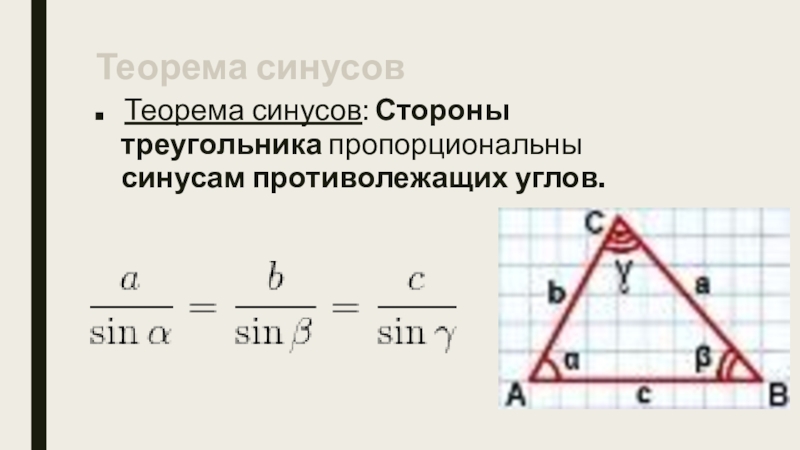
- 4. Теорема синусов Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.
- 5. Расширенная теорема синусов.Для произвольного треугольника имеет место соотношение:
- 6. Доказательство теоремы синусов.Доказательство:Пусть в треугольнике ABC AB=c,
- 7. Примеры решения задач. Пример 1.
- 8. Решение 1 примера.
- 9. Пример 2.
- 10. Решение примера 2.
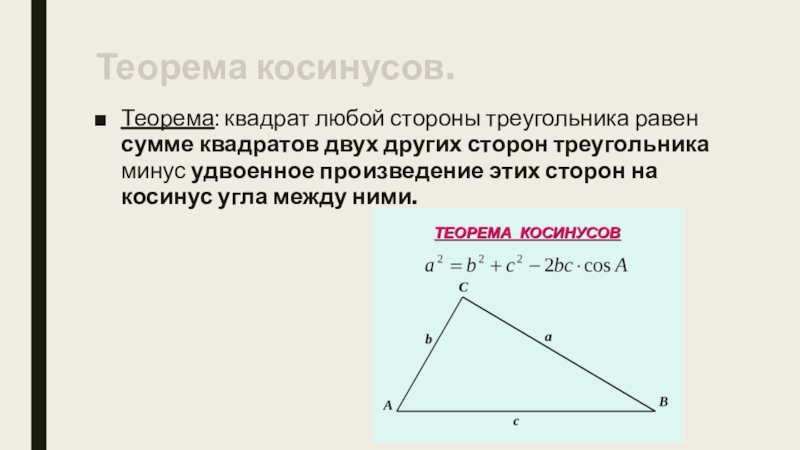
- 11. Теорема косинусов.Теорема: квадрат любой стороны треугольника равен
- 12. Доказательство теоремы косинусов. Доказательство:Пусть в треугольнике
- 13. Важно знать!!!Теорему косинусов называют иногда обобщенной теоремой
- 14. Примеры решения задач. Пример 1.
- 15. Решение примера 1.
- 16. Пример 2.
- 17. Решение примера 2.
- 18. Задачи для самостоятельного решения.Задача 1Гипотенуза АВ прямоугольного
- 19. Задача 3Четырехугольник АВСД вписан в окружность. Известно,
- 20. Спасибо за урок!!!
ПовторениеВспомним тему «Площадь треугольника». С помощью каких формул мы можем определить площадь треугольника?Ответ:
Слайд 1Основные способы решения задач планиметрии.
Теоремы косинусов и синусов.
Малыкина Елена Александровна
учитель математики
высшей квалификационной категории
«Лицея №78 им. А.С.Пушкина».
Слайд 2Повторение
Вспомним тему «Площадь треугольника». С помощью каких формул мы можем определить
площадь треугольника?
Ответ:
Ответ:
Слайд 4Теорема синусов
Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.
Слайд 6Доказательство теоремы синусов.
Доказательство:
Пусть в треугольнике ABC AB=c, BC=a, CA=b.
По теореме
о площади треугольника: S=1/2absinC, S=1/2bcsinA, S=1/2casinB
Из первых двух равенств получаем: 1/2absinC=1/2bcsinA,
откуда = .
Точно также из второго и третьего равенств следует: = .
Итак, .
Теорема доказана.
Из первых двух равенств получаем: 1/2absinC=1/2bcsinA,
откуда = .
Точно также из второго и третьего равенств следует: = .
Итак, .
Теорема доказана.
Слайд 11Теорема косинусов.
Теорема: квадрат любой стороны треугольника равен сумме квадратов двух других
сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
Слайд 12Доказательство теоремы косинусов.
Доказательство:
Пусть в треугольнике ABC AB=c, BC=a, CA=b.
Введем систему
координат с началом в точке A так, как показано на рисунке. Тогда точка B имеет координаты (c;0), а точка C имеет координаты (bcosA; bsinA). По формуле расстояния между двумя точками получаем:
BC2 = a2= (bcosA-c)2+ b2sin2A= b2cos2A+ b2sin2A-2bccosA+c2=b2+c2-2bccosA
Теорема доказана.
BC2 = a2= (bcosA-c)2+ b2sin2A= b2cos2A+ b2sin2A-2bccosA+c2=b2+c2-2bccosA
Теорема доказана.
Слайд 13Важно знать!!!
Теорему косинусов называют иногда обобщенной теоремой Пифагора. Такое название объясняется
тем, что в теореме косинусов содержится как частный случай теорема Пифагора. В самом деле, если в треугольнике ABC угол A прямой, то cosA=cos900 = 0 и по формуле
Получаем: a2 = b2+c2 , то есть квадрат гипотенузы равен сумме квадратов катетов.
Получаем: a2 = b2+c2 , то есть квадрат гипотенузы равен сумме квадратов катетов.
Слайд 18Задачи для самостоятельного решения.
Задача 1
Гипотенуза АВ прямоугольного треугольника АВС равна 18,
катет ВС=6. На гипотенузе взята точка М такая, что АМ:МВ=1:2. Найдите СМ.
Задача 2
Известны стороны треугольника АВС: АВ=c, BC=a, AC=b. Найти длину медианы треугольника, проведенную к стороне ВС.
Задача 2
Известны стороны треугольника АВС: АВ=c, BC=a, AC=b. Найти длину медианы треугольника, проведенную к стороне ВС.
Слайд 19Задача 3
Четырехугольник АВСД вписан в окружность. Известно, что АВ=3, ВС=4, СД=5
и АД=2. Найти диагональ АС.
Задача 4
Дан треугольник АВС, в котором АС=10 и
Задача 4
Дан треугольник АВС, в котором АС=10 и