- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Неевклидовы геометрии
Содержание
- 1. Неевклидовы геометрии
- 2. Введение.Геометрия — раздел математики, изучающий пространственные структуры
- 3. Коренные изменения связаны с работами Лобачевского в
- 4. Постулаты Евклида. Евклид —
- 5. Из истории неевклидовой геометрии.Первым неевклидовым геометром,
- 6. Ближе всех подошел к цели иезуит, логик
- 7. Вскоре он отверг гипотезу о тупом угле
- 8. ЧЕТЫРЕХУГОЛЬНИК САККЕРИ - четырехугольник BCED с BC
- 9. К. Гаусса (1777-1855) принято считать одним из
- 10. Но, опасаясь насмешек, он воздерживался от публикации
- 11. В своем доказательстве того, что внешний угол
- 12. Геометрия Лобачевского.Попытки доказать V постулат привели
- 13. Заменив этой аксиомой V постулат Евклида, Лобачевский
- 14. Внутри круга любого конечного радиуса существует множество
- 15. Из аксиомы Лобачевского вытекают следующие логические следствия:1. Если
- 16. 2. Через точку С, лежащую вне прямой
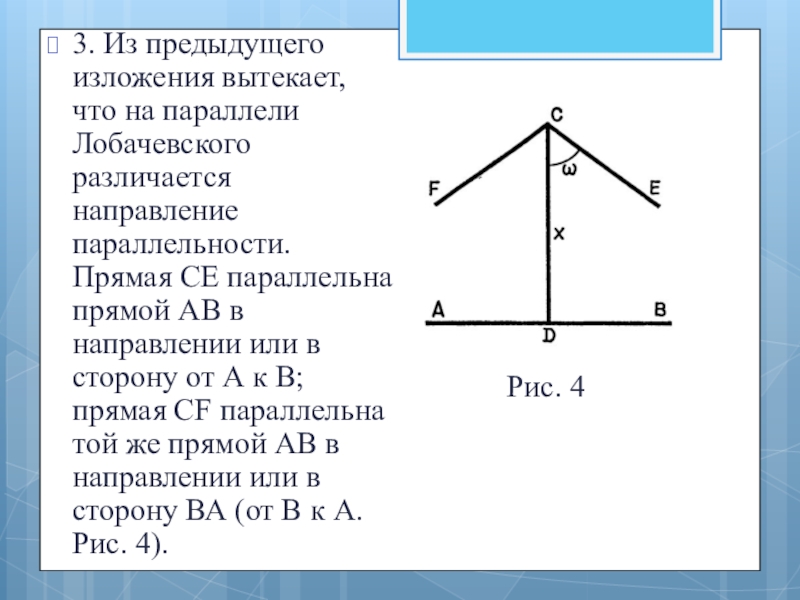
- 17. 3. Из предыдущего изложения вытекает, что на
- 18. Приведем некоторые другие понятия и факты геометрии
- 19. Однако идеи Лобачевского были настолько революционными и
- 20. Тогда же итальянский математик, профессор Римского университета
- 21. Псевдосфера – это поверхность в обыкновенном реальном
- 22. Одним из важнейших результатов открытия геометрии Лобачевского
- 23. Итак, плоскость Римана представлена евклидовой сферой. На
- 24. Одним словом, большие окружности сферы — это
- 25. Таковы некоторые из основных идей и фактов
- 26. Заключение.Возникшие из попыток доказательства V постулата, неевклидовы
- 27. Открытие неевклидовой геометрии, начало которому положил Лобачевский,
- 28. Спасибо за внимание
Слайд 1Неевклидовы геометрии
Выполнила ученица 11 класса
МКОУ Калачеевская СОШ№6
Чепуркова Анна Эдуардовна
Слайд 2Введение.
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также
более 2000 лет образцом строгого
дедуктивного изложения геометрии.
Слайд 3
Коренные изменения связаны с работами Лобачевского в 1829 году, который отказался
Слайд 4Постулаты Евклида.
Евклид — древнегреческий математик, автор первого
Постулаты Евклида представляют собой правила построения с помощью идеального циркуля и идеальной линейки (рис.1):
I. Всякие две точки можно соединить прямой линией;
II. Ограниченную прямую линию можно неограниченно продолжить;
III. Из всякого центра всяким радиусом можно описать окружность;
IV. Все прямые углы равны между собой;
V. Если прямая падает на две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то при неограниченном продолжении этих двух прямых они пересекутся с той стороны, где углы меньше двух прямых. Другая формулировка пятого постулата (аксиомы параллельности), гласит: Через точку вне прямой в их плоскости можно провести не более одной прямой, не пересекающей данную прямую.
Слайд 5Из истории
неевклидовой геометрии.
Первым неевклидовым геометром,
вероятно, можно считать самого
С первого века до н.э. до 1820 математики пытались вывести пятый постулат из остальных, но преуспели лишь в замене его различными эквивалентными допущениями, такими, как "две параллельные линии всюду равно удалены друг от друга" или "любые три точки, не расположенные на одной прямой, принадлежат окружности".
Слайд 6
Ближе всех подошел к цели иезуит, логик и математик Дж.Саккери (1667-1733),
что верхние углы прямые,
доказав, что любая другая гипотеза
приводит к противоречию.
Слайд 7
Вскоре он отверг гипотезу о тупом угле (и тем самым лишил
Слайд 8
ЧЕТЫРЕХУГОЛЬНИК САККЕРИ - четырехугольник BCED с BC = ED и прямыми
Слайд 9
К. Гаусса (1777-1855) принято считать одним из величайших математиков всех времен.
К. Гаусс
Слайд 10
Но, опасаясь насмешек, он воздерживался от публикации этих идей и тем
В 1854 Б. Риман (1826-1866) заметил, что из неограниченности пространства еще не следует его бесконечная протяженность. Смысл этого утверждения станет яснее, если представить, что в неограниченной, но конечной вселенной астроном в принципе мог бы увидеть в телескоп, обладающий достаточно высокой разрешающей способностью, свой собственный затылок (если отвлечься от небольшой детали, связанной с тем, что свет, отраженный от затылка, достиг бы глаза астронома через тысячи миллионов лет).
Янош Бояй
Слайд 11
В своем доказательстве того, что внешний угол при любой вершине треугольника
Бернхард Риман
Слайд 12Геометрия
Лобачевского.
Попытки доказать V постулат привели Лобачевского к мысли о том,
Но если V постулат не зависит от других аксиом, то , допуская все другие аксиомы (абсолютной геометрии), можно принять или не принять евклидов постулат. Если же вместо евклидовой аксиомы параллельности принять другую, ей не эквивалентную, получим новую, неевклидову геометрию. Лобачевский и сформулировал новую аксиому параллельных: «Через точку вне прямой можно провести не только одну прямую, не встречающую данной прямой, а по крайней мере две».
Николай Иванович Лобачевский (1792-1856) русский математик, один из создателей неевклидовой геометрии, деятель университетского образования и народного просвещения.
Слайд 13
Заменив этой аксиомой V постулат Евклида, Лобачевский разработал свою неевклидову геометрию,
Аксиома Лобачевского нам кажется на первый взгляд странной, так как противоречит нашим установившимся геометрическим представлениям. Однако при более глубоком анализе вопроса нужно признать, что в отличие от других аксиом, касающихся фигур ограниченных размеров, аксиома параллельности Евклида относится к неограниченной прямой и никогда не может быть проверена с помощью непосредственного эксперимента, который может быть проведен лишь в ограниченной части пространства. Если, например, взять угол NCL достаточно малым, то отрезки CL и АВ не пересекутся даже на расстоянии, выходящем за пределы нашей планеты. И вот как раз в пределах ограниченной части плоскости можно провести через данную точку множество прямых, не пересекающих данной прямой.
Рис. 1
Слайд 14
Внутри круга любого конечного радиуса существует множество «прямых» (т.е. хорд), проходящих
Рис. 2
Слайд 15
Из аксиомы Лобачевского вытекают следующие логические следствия:
1. Если прямые CN и CL
Слайд 16
2. Через точку С, лежащую вне прямой АВ, проходят в плоскости
Рис. 3
Слайд 17
3. Из предыдущего изложения вытекает, что на параллели Лобачевского различается направление
Рис. 4
Слайд 18
Приведем некоторые другие понятия и факты геометрии Лобачевского.
Функция Лобачевского.
2. Сумма углов
3. Сумма углов четырехугольника меньше360º
4. Внешний угол треугольника больше суммы внутренних, с ним не смежных углов.
5. Если три угла одного треугольника соответственно равны трем углам другого треугольника, то эти треугольники равны между собой. Это четвертый признак равенства треугольников в геометрии Лобачевского. Отсюда ясно, что в геометрии Лобачевского нет подобных фигур.
6. площадь треугольника прямо пропорциональна его угловому дефекту.
Слайд 19
Однако идеи Лобачевского были настолько революционными и до того опередили свой
Слайд 20
Тогда же итальянский математик, профессор Римского университета Эудженио Бельтрами нашел модель
Слайд 21
Псевдосфера – это поверхность в обыкновенном реальном пространстве, на которой выполняются
Слайд 22
Одним из важнейших результатов открытия геометрии Лобачевского (называемой также гиперболической геометрией)
Слайд 23
Итак, плоскость Римана представлена евклидовой сферой. На сфере нет прямых линий,
Рис. 5
Слайд 24
Одним словом, большие окружности сферы — это ее «прямые» (рис. 11).
В разработку эллиптической геометрии значительный вклад внес Гаусс своими исследованиями о поверхностях.
Рис. 6
Слайд 25
Таковы некоторые из основных идей и фактов геометрии Лобачевского.
После работы «О
Слайд 26Заключение.
Возникшие из попыток доказательства V постулата, неевклидовы геометрии, открытые Лобачевским, Бояй,