- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Многовариантные задачи в планиметрии
Содержание
- 1. Многовариантные задачи в планиметрии
- 2. Тип задания: планиметрическая задача на вычисление длин,
- 3. Задача «Лампочка».Вообразите, что у вас перегорела лампочка.
- 4. Тест на внимание
- 5. Нужно быть предельно внимательным, читая условие задачи,
- 6. Выявление многовариантных задач:точка или принадлежит отрезку АВ,
- 7. Для того, чтобы научиться решать
- 8. Сколько существует случаев взаимного расположения трех точек на прямой?
- 9. 1.Сколько существует окружностей с центром в точке (5;0), касающихся данной окружности.
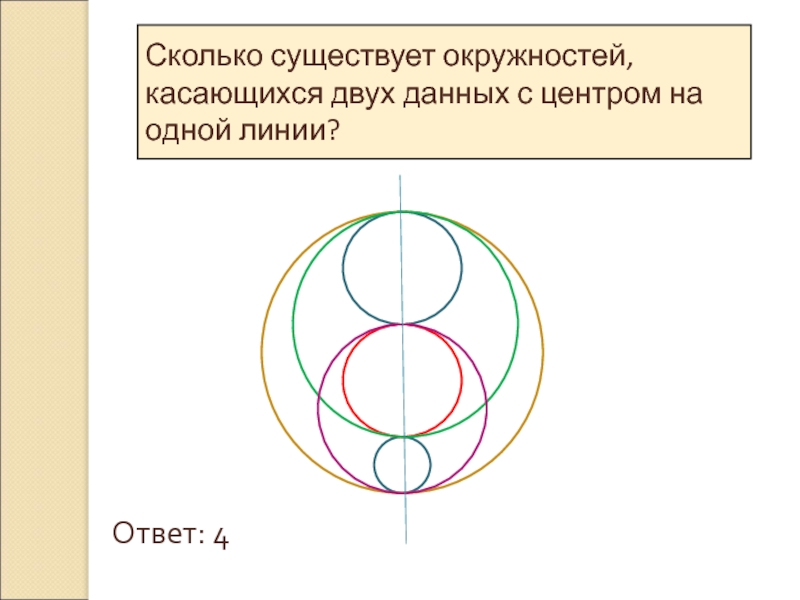
- 10. Сколько существует окружностей, касающихся двух данных с центром на одной линии?Ответ: 4
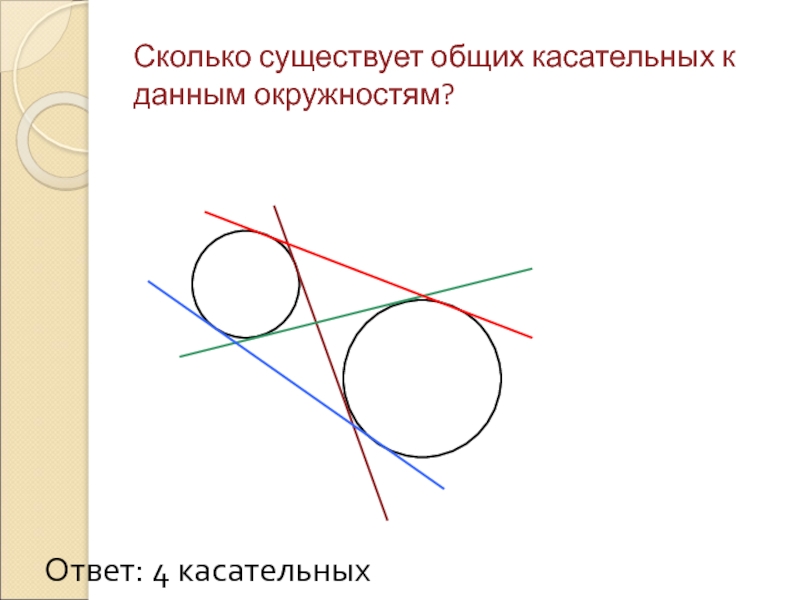
- 11. Сколько существует общих касательных к данным окружностям? Ответ: 4 касательных
- 12. Сколько окружностей можно вписать в параллелограмм, так,
- 13. Обратите вниманиеУсловие задачи не определяет взаимное расположения
- 14. «Геометрия полна приключений, потому что за каждой
- 15. Если вы хотите научиться плавать, то смело
Слайд 2Тип задания: планиметрическая задача на вычисление длин, площадей, углов.
Для успешного решения
Слайд 3Задача «Лампочка».
Вообразите, что у вас перегорела лампочка. Чем вы её замените,
Слайд 5
Нужно быть предельно внимательным, читая условие задачи, продумать: нет ли других
Кроме того существуют некоторые закономерности, учет которых позволит не пропустить решение.
Слайд 6Выявление многовариантных задач:
точка или принадлежит отрезку АВ, или ему не принадлежит,
Различные положения центра описанной окружности или ортоцентра треугольника в зависимости от вида треугольника(остроугольный, прямоугольный, тупоугольный)
В условии задачи фигурируют две касающиеся окружности, но не указан способ касания: внешний или внутренний.
В задаче даны две точки, делящие окружность на две дуги, кроме того известно, что некоторая прямая касается окружности, но не указано, на какой из двух дуг лежит точка касания.
В условии сказано, что треугольник ABC равнобедренный, но не сказано, какие пары сторон равны
Точка М делит отрезок АВ на отрезки длиной а, и b, однако не сказано, какой из них a а какой – b.
Известно, что угол между пересекающимися прямыми равен α, однако не сказано какой из углов
Слайд 7 Для того, чтобы научиться решать многовариантные задачи, конечно, нужна тренировка!
Слайд 12Сколько окружностей можно вписать в параллелограмм, так, чтобы они касались двух
Слайд 13
Обратите внимание
Условие задачи не определяет
взаимное расположения точек и фигуры
В условии
касающиеся окружности, но не указан
способ касания.
В задаче фигурируют объекты, которым
приписываются определенные свойства, но не
указан порядок соответствия между множеством
объектов и множеством их свойств
Неоднозначность
трактовки
Слайд 14«Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли.
Слайд 15Если вы хотите научиться плавать, то смело входите в воду, а
Как научиться видеть, что решение конкретной задачи требует рассмотрения нескольких случаев, а не «хвататься» лишь за разбор того, который лежит на поверхности? Как вы поняли, вопрос этот чрезвычайно сложный. Трудно предложить полный список конкретных рекомендаций, которые могут застраховать абитуриента от неполных решений. Обнаружить «замаскированность двойного дна» поможет опыт, интуиция, сообразительность.
Чтобы научиться читать, надо читать, чтобы научиться решать коварные задачи, надо именно их решать. Вот и вся премудрость.