- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Многогранники
Содержание
- 1. Многогранники
- 2. Содержание МногогранникВыпуклый многогранникСписок правильных многогранниковКомбинаторные свойстваГеометрические свойстваРадиусы,
- 3. МногогранникМногогранник — поверхность, составленная из многоугольников и ограничивающих некоторое геометрическое
- 4. Выпуклый многогранникМногогранник называется выпуклым, если он весь расположен
- 5. Список правильных многогранниковСуществует всего пять правильных многогранников.
- 6. Комбинаторные свойстваЭйлером была выведена формула, связывающая число вершин
- 7. Геометрические свойстваС каждым правильным многогранником связаны определённые углы,
- 8. Радиусы, площади и объёмыС каждым правильным многогранником
- 9. ИсторияПравильные многогранники известны с древнейших времён. Их
- 10. Звёздчатые многогранникиВо всех пространствах размерности n > 4 существует
- 11. Двойственные многогранникиМногогранник, двойственный (или дуальный) к заданному многограннику — многогранник,
- 12. Изгибаемые многогранникиМногогранник (точнее — многогранная поверхность) называется изгибаемым, если его
- 13. Сделай самСделать модель изгибаемого многогранника Штеффена совсем
- 14. Перестановочный многогранникВ математике перестановочный многогранник порядка n — это (n − 1)-мерный выпуклый многогранник, вложенный
- 15. Замощение пространстваПерестановочный многогранник порядка n полностью содержится в (n − 1)-мерной
- 16. Галерея
- 17. ТетраэдрТетра́эдр (греч. τετραεδρον — четырёхгранник) — многогранник с четырьмя треугольными гранями,
- 18. Объем тетраэдраОбъем тетраэдра (с учетом знака), равенТетраэдры
- 19. Гексаэдр (куб)Куб или правильный гексаэдр — правильный многогранник, каждая грань которого
- 20. ОктаэдрОкта́эдр (греч. οκτάεδρον, от греч. οκτώ, «восемь» и греч. έδρα — «основание») — один из
- 21. ДодекаэдрДодека́эдр (от греч. δώδεκα — двенадцать и εδρον — грань), двенадцатигранник —правильный многогранник, составленный
- 22. Основные формулыЕсли за длину ребра принять a, то
- 23. ПентагондодекаэдрВизуально очень похож на платоновское тело, но
- 24. ИкосаэдрИкоса́эдр (от греч. εικοσάς — двадцать; -εδρον — грань, лицо, основание) — правильный выпуклый
- 25. Усечённый икосаэдрУсечённый икосаэдр - многогранник, состоящий из 12
Слайд 1Мультимедийная разработка
на тему:
«Многогранники»
Выполнила: преподаватель математики Валишева Н.А.
Слайд 2Содержание
Многогранник
Выпуклый многогранник
Список правильных многогранников
Комбинаторные свойства
Геометрические свойства
Радиусы, площади и объёмы
История
Звёздчатые многогранники
Двойственные
Изгибаемые многогранники
Сделай сам
Перестановочный многогранник
Замощение пространства
Галерея
Тетраэдр
Объём тетраэдра
Гексаэдр (куб)
Октаэдр
Додекаэдр
Икосаэдр
Усечённый икосаэдр
Слайд 3Многогранник
Многогранник — поверхность, составленная из многоугольников и ограничивающих некоторое геометрическое тело.
Многогранник, точнее трёхмерный многогранник — совокупность
каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного), называемого смежным с первым (по этой стороне);
(связность) от любого из многоугольников, составляющих многогранник, можно дойти до любого из них, переходя к смежному с ним, а от этого, в свою очередь, к смежному с ним, и т. д.
Эти многоугольники называются гранями, их стороны — рёбрами, а их вершины —вершинами многогранника. Простейшими примерами многогранников являются выпуклые многогранники, т.е. граница ограниченного подмножества евклидова пространства являющееся пересечением конечного числа полупространств.
Приведенное определение многогранника получает различный смысл в зависимости от того, как определить многоугольник, возможны следующие два варианта:
Плоские замкнутые ломаные (хотя бы и самопересекающиеся);
Части плоскости, ограниченные ломаными.
В последнем случае многогранник есть поверхность, составленная из многоугольных кусков.
Если эта поверхность сама себя не пересекает, то она есть полная поверхность некоторого геометрического тела, которое также называется многогранником; отсюда возникает третье определение.
Слайд 4Выпуклый многогранник
Многогранник называется выпуклым, если он весь расположен по одну сторону от
Вариации и обобщения
Понятие многогранника индуктивно обобщается по размерности, и обычно называется n-мерный многогранник.
Бесконечный многогранник допускает в определении конечное число неограниченных граней и рёбер
Криволинейные многогранники допускают криволинейные рёбра и грани.
Правильный многогранник, или Платоново тело — это выпуклый многогранник с максимально возможной симметрией.
Многогранник называется правильным, если:
Он выпуклый;
Все его грани являются равными правильными многоугольниками;
В каждой его вершине сходится одинаковое число рёбер.
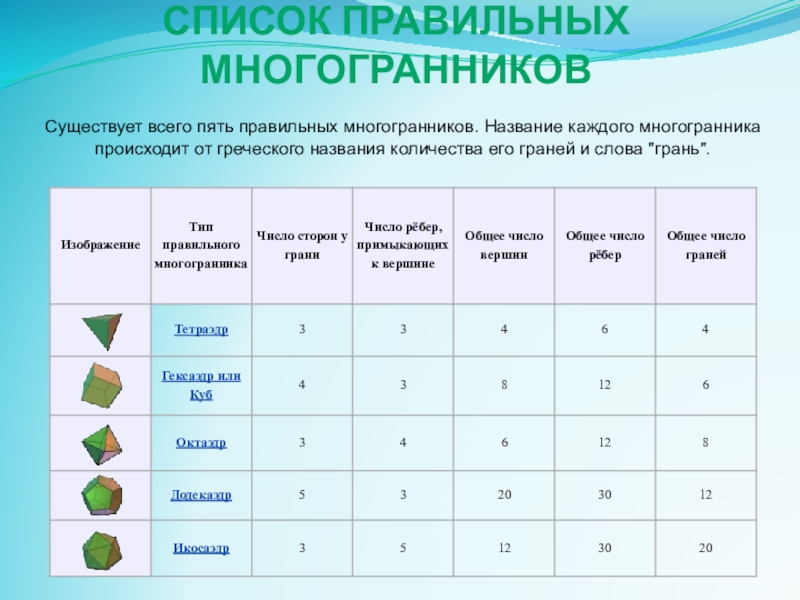
Слайд 5Список правильных многогранников
Существует всего пять правильных многогранников. Название каждого многогранника происходит
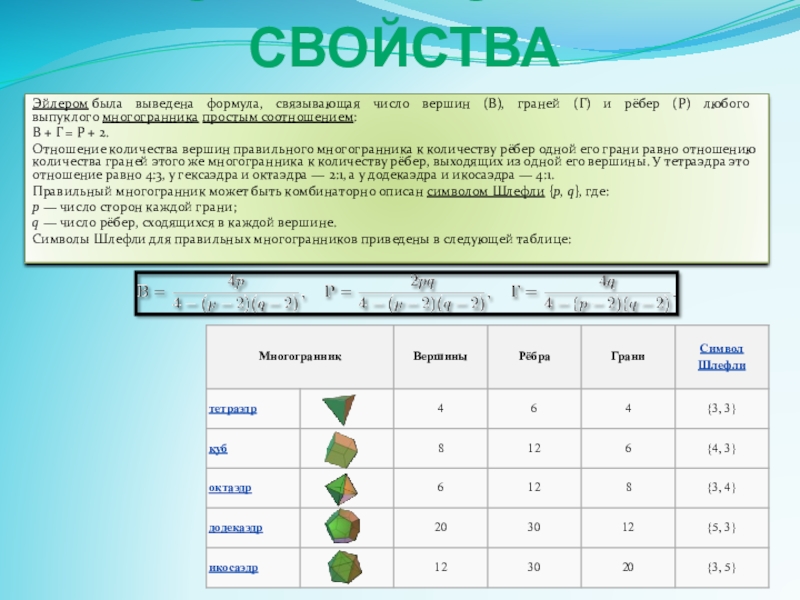
Слайд 6Комбинаторные свойства
Эйлером была выведена формула, связывающая число вершин (В), граней (Г) и
В + Г = Р + 2.
Отношение количества вершин правильного многогранника к количеству рёбер одной его грани равно отношению количества граней этого же многогранника к количеству рёбер, выходящих из одной его вершины. У тетраэдра это отношение равно 4:3, у гексаэдра и октаэдра — 2:1, а у додекаэдра и икосаэдра — 4:1.
Правильный многогранник может быть комбинаторно описан символом Шлефли {p, q}, где:
p — число сторон каждой грани;
q — число рёбер, сходящихся в каждой вершине.
Символы Шлефли для правильных многогранников приведены в следующей таблице:
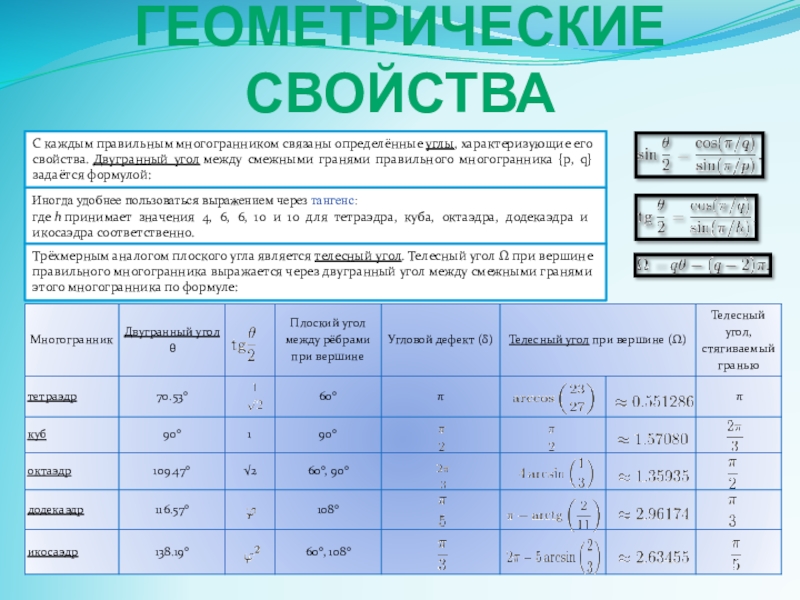
Слайд 7Геометрические свойства
С каждым правильным многогранником связаны определённые углы, характеризующие его свойства. Двугранный угол между
Иногда удобнее пользоваться выражением через тангенс:
где h принимает значения 4, 6, 6, 10 и 10 для тетраэдра, куба, октаэдра, додекаэдра и икосаэдра соответственно.
Трёхмерным аналогом плоского угла является телесный угол. Телесный угол Ω при вершине правильного многогранника выражается через двугранный угол между смежными гранями этого многогранника по формуле:
Слайд 8Радиусы, площади и объёмы
С каждым правильным многогранником связаны три концентрические сферы:
Описанная
Срединная сфера, касающаяся каждого его ребра в середине;
Вписанная сфера, касающаяся каждой его грани в её центре.
Радиусы описанной (R) и вписанной (r) сфер задаются формулами:
где θ - двугранный угол между смежными гранями многогранника. Радиус срединной сферы задаётся формулой:
где h - величина описанная выше, при определении двугранных углов (h = 4, 6, 6, 10 или 10). Отношения описанных радиусов к вписанным радиусам симметрично относительно p и q:
Площадь поверхности S правильного многогранника {p, q} вычисляется, как площадь правильного p-угольника, умноженная на число граней Г:
Объём правильного многогранника вычисляется, как умноженный на число граней объём правильной пирамиды, основанием которой служит правильный p-угольник, а высотой — радиус вписанной сферы r:
Константы φ и ξ задаются выражениями
Слайд 9История
Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти
В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.
Правильные многогранники характерны для философии Платона, в честь которого и получили название «платоновы тела». Платон писал о них в своём трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику. Земля сопоставлялась кубу, воздух — октаэдру, вода — икосаэдру, а огонь — тетраэдру. Для возникновения данных ассоциаций были следующие причины: жар огня ощущается чётко и остро (как маленькие тетраэдры); воздух состоит из октаэдров: его мельчайшие компоненты настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков (к которым ближе всего икосаэдры); в противоположность воде, совершенно непохожие на шар кубики составляют землю, что служит причиной тому, что земля рассыпается в руках, в противоположность плавному току воды. По поводу пятого элемента, додекаэдра, Платон сделал смутное замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца». Аристотель добавил пятый элемент — эфир и постулировал, что небеса сделаны из этого элемента, но он не сопоставлял его платоновскому пятому элементу.
Евклид дал полное математическое описание правильных многогранников в последней, XIII книге Начал. Предложения 13—17 этой книги описывают структуру тетраэдра, октаэдра, куба, икосаэдра и додекаэдра в данном порядке. Для каждого многогранника Евклид нашёл отношение диаметра описанной сферы к длине ребра. В 18-м предложении утверждается, что не существует других правильных многогранников. Андреас Шпейзер отстаивал точку зрения, что построение пяти правильных многогранников является главной целью дедуктивной системы геометрии в том виде, как та была создана греками и канонизирована в «Началах» Евклида[1]. Большое количество информации XIII книги «Начал», возможно, взято из трудов Теэтета.
В XVI веке немецкий астроном Иоганн Кеплер пытался найти связь между пятью известными на тот момент планетами Солнечной системы (исключая Землю) и правильными многогранниками. В «Тайне мира», опубликованной в 1596 году, Кеплер изложил свою модель Солнечной системы. В ней пять правильных многогранников помещались один в другой и разделялись серией вписанных и описанных сфер. Каждая из шести сфер соответствовала одной из планет (Меркурию, Венере, Земле, Марсу, Юпитеру и Сатурну). Многогранники были расположены в следующем порядке (от внутреннего к внешнему): октаэдр, за ним икосаэдр, додекаэдр, тетраэдр и, наконец, куб. Таким образом, структура Солнечной системы и отношения расстояний между планетами определялись правильными многогранниками. Позже от оригинальной идеи Кеплера пришлось отказаться, но результатом его поисков стало открытие двух законов орбитальной динамики — законов Кеплера, — изменивших курс физики и астрономии, а также правильных звёздчатых многогранников (тел Кеплера-Пуансо).
Слайд 10Звёздчатые многогранники
Во всех пространствах размерности n > 4 существует только 3 типа правильных
Звёздчатый многогранник (звёздчатое тело) — это многогранник, грани которого пересекаются между собой. Как и у незвёздчатых многогранников грани попарно соединяются в рёбрах. При этом внутренние линии пересечения не считаются рёбрами.
Звёздчатой формой многогранника называется многогранник, полученный путём продления граней данного многогранника через рёбра до их следущего пересечения с другими гранями по новым рёбрам.
Правильные звёздчатые многогранники - это звёздчатые многогранники, гранями которых являются одинаковые правильные или звёздчатые многоугольники. Коши установил, что существует всего 4 правильных звёздчатых тела, не являющиеся соединениями платоновых и звёздчатых тел, называемые телами Кепплера-Пуансо: все 3 звёздчатых формы додекаэдра и одна из звёздчатых форм икосаэдра. Остальные правильные звёздчатые многогранники являются или соединениями платоновых тел, или соединениями тел Кепплера-Пуансо.
Многие формы звёздчатых многогранников подсказывает сама природа. Например Снежинки — это плоские проекции звёздчатых многогранников. Некоторые молекулы имеют правильные структуры объёмных фигур.
Всего существует 6 правильных четырёхмерных многогранников:
Слайд 11Двойственные многогранники
Многогранник, двойственный (или дуальный) к заданному многограннику — многогранник, у которого каждой грани
Построение
Простейший способ построения двойственного многогранника таков:
Вершины: находятся в центре граней исходного многогранника.
Рёбра: между вершинами проводится ребро, если соответствующие грани имеют общее ребро.
Слайд 12Изгибаемые многогранники
Многогранник (точнее — многогранная поверхность) называется изгибаемым, если его пространственную форму можно изменить
Свойства и примеры
В теории изгибаемых многогранников известно немало красивых и нетривиальных утверждений. Ниже приведены наиболее важные из установленных на сегодня фактов, придерживаясь хронологического порядка:
Никакой выпуклый многогранник не может быть изгибаемым. Это немедленно вытекает из теоремы Коши об однозначной определённости выпуклого многогранника, доказанной в 1813 году.
Первые примеры изгибаемых многогранников были построены бельгийским инженером и математиком Раулем Брикаром в 1897 году. Сейчас их называют октаэдрами Брикара. Они не только невыпуклые, но и имеют самопересечения, что не позволяет построить их движущуюся картонную модель.
В 1976 году американский математик Роберт Коннелли впервые построил изгибаемый многогранник без самопересечений.
Из всех известных на сегодняшний день изгибаемых многогранников без самопересечений наименьшее число вершин (девять) имеет многогранник, построенный немецким математиком Клаусом Штеффеном (нем. Klaus Steffen).
Известны примеры изгибаемых многогранников, являющихся реализациями тора или бутылки Клейна или вообще двумерной поверхности любого топологического рода.
Теорема Сабитова: Любой изгибаемый многогранник в процессе изгибания сохраняет свой объём, то есть он будет изгибаться даже если его заполнить несжимаемой жидкостью.
Слайд 13Сделай сам
Сделать модель изгибаемого многогранника Штеффена совсем не трудно. Опишем это
Сохраните файл с развёрткой многогранника Штеффена из приведённой выше «галереи изображений».
Увеличьте развёртку в 2—3 раза и распечатайте его на принтере (при этом желательно использовать плотную бумагу или полукартон).
Вырежьте развёртку по контуру, состоящему из красных, синих и чёрных (сплошных и пунктирных) отрезков.
Несколько раз перегните бумагу по оставшимся на развёртке сплошным и пунктирным отрезкам. Выполняя последующие действия следует придавать поверхности такую форму, чтобы сплошные отрезки были «горными хребтами» (то есть выступали из многогранника наружу), а пунктирные отрезки были «долинами» (то есть вдавались бы внутрь многогранника).
Изогните поверхность в пространстве и склейте между собой каждые два чёрных отрезка, соединённых на развёртке зелёной дугой окружности.
Склейте между собой два синих отрезка.
Склейте между собой два красных отрезка.
Модель многогранника Штеффена готова.
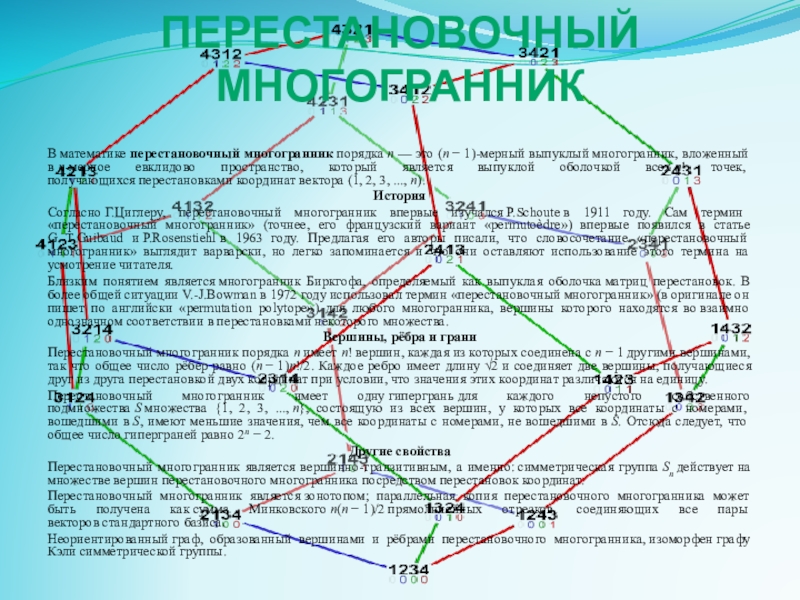
Слайд 14Перестановочный многогранник
В математике перестановочный многогранник порядка n — это (n − 1)-мерный выпуклый многогранник, вложенный в n-мерное евклидово пространство, который
История
Согласно Г.Циглеру, перестановочный многогранник впервые изучался P.Schoute в 1911 году. Сам термин «перестановочный многогранник» (точнее, его французский вариант «permutoèdre») впервые появился в статье G.-T.Guibaud и P.Rosenstiehl в 1963 году. Предлагая его авторы писали, что словосочетание «перестановочный многогранник» выглядит варварски, но легко запоминается и что они оставляют использование этого термина на усмотрение читателя.
Близким понятием является многогранник Биркгофа, определяемый как выпуклая оболочка матриц перестановок. В более общей ситуации V.-J.Bowman в 1972 году использовал термин «перестановочный многогранник» (в оригинале он пишет по английски «permutation polytope») для любого многогранника, вершины которого находятся во взаимно однозначном соответствии в перестановками некоторого множества.
Вершины, рёбра и грани
Перестановочный многогранник порядка n имеет n! вершин, каждая из которых соединена с n − 1 другими вершинами, так что общее число рёбер равно (n − 1)n!/2. Каждое ребро имеет длину √2 и соединяет две вершины, получающиеся друг из друга перестановкой двух координат при условии, что значения этих координат различаются на единицу.
Перестановочный многогранник имеет одну гипергрань для каждого непустого собственного подмножества S множества {1, 2, 3, ..., n}, состоящую из всех вершин, у которых все координаты с номерами, вошедшими в S, имеют меньшие значения, чем все координаты с номерами, не вошедшими в S. Отсюда следует, что общее число гиперграней равно 2n − 2.
Другие свойства
Перестановочный многогранник является вершинно-транзитивным, а именно: симметрическая группа Sn действует на множестве вершин перестановочного многогранника посредством перестановок координат.
Перестановочный многогранник является зонотопом; параллельная копия перестановочного многогранника может быть получена как сумма Минковского n(n − 1)/2 прямолинейных отрезков, соединяющих все пары векторов стандартного базиса.
Неориентированный граф, образованный вершинами и рёбрами перестановочного многогранника, изоморфен графу Кэли симметрической группы.
Слайд 15Замощение пространства
Перестановочный многогранник порядка n полностью содержится в (n − 1)-мерной гиперплоскости, состоящей из всех
1 + 2 + … + n = n(n + 1)/2.
Более того, эта гиперплоскость может быть замощена бесконечным количеством параллельных копий перестановочного многогранника. Каждая из этих копий отличается от исходного перестановочного многогранника на элемент некоторой (n − 1)-мерной решётки, образованной n-мерными векторами, все координаты которых целочисленные, их сумма равна нулю, причём все координаты принадлежат одному классу вычетов по модулю n:
x1 + x2 + … + xn = 0, x1 ≡ x2 ≡ … ≡ xn (mod n).
Например, перестановочный многогранник порядка 4, изображённый на рисунке, замощает 3-мерное пространство посредством параллельных переносов. Здесь 3-мерное пространство рассматривается как аффинное подпространство 4-мерноего пространства R4 с координатами x, y, z, w, которое образовано четвёрками вещественных чисел, сумма которых равна 10, т.е.
x + y + z + w = 10.
Легко проверить, что для каждого из следующих четырёх векторов
(1,1,1,−3), (1,1,−3,1), (1,−3,1,1) и (−3,1,1,1),
сумма координат равна нулю и все координаты сравнимы с 1 по модулю 4. Любые три из этих векторов порождают решётку параллельных переносов.
Замощения, построенные таким способом из перестановочных многогранников порядка 3 и 4, являются замощением правильными шестиугольниками и замощением усечёнными октаэдрами соответственно.
Слайд 17Тетраэдр
Тетра́эдр (греч. τετραεδρον — четырёхгранник) — многогранник с четырьмя треугольными гранями, в каждой из вершин
Свойства тетраэдра
Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдрапараллелепипед.
Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины.
Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.
Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
Теорема. Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, считая от вершины. Эта точка делит бимедианы пополам.
Выделяют:
равногранный тетраэдр, у которого все грани - равные между собой треугольники;
ортоцентрический тетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке;
прямоугольный тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой;
правильный тетраэдр, у которого все грани - равносторонние треугольники;
каркасный тетраэдр — тетраэдр, отвечающий любому из условий
Существует сфера, касающаяся всех ребер.
Суммы длин скрещивающихся ребер равны.
Суммы двугранных углов при противоположных ребрах равны.
Окружности, вписанные в грани, попарно касаются.
Все четырехугольники, получающиеся на развертке тетраэдра, — описанные.
Перпендикуляры, восставленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.
соразмерный тетраэдр, все бивысоты которого равны;
инцентрический тетраэдр, у которого отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Слайд 18Объем тетраэдра
Объем тетраэдра (с учетом знака), равен
Тетраэдры в микромире
Вода, Лёд, Н2О
Молекула метана СН4
Молекула аммиака NH3
Алмаз C -
Флюорит CaF2, тетраэдр с ребром равным 3, 8626 ангстрем
Сфалерит, ZnS, тетраэдр с ребром равным 3,823 ангстрем
Комплексные ионы [BF4] -, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+.
Тетраэдры в технике
Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм мостов и т.д. Стержни испытывают только продольные нагрузки.
Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Граф четверичного триггера представляет собой тетраэдр
Слайд 19Гексаэдр (куб)
Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай
В различных дисциплинах используются значения термина, имеющие отношения к тем или иным свойствам геометрического прототипа. В частности, в аналитике (OLAP-анализ) применяются так называемые аналитические многомерные кубы, позволяющие в наглядном виде сопоставить данные из различных таблиц.
Свойства куба
Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его главным диагоналям.
В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным.
В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.
Диагональю куба называют отрезок, соединяющий две вершины, симметричные относительно центра куба. Диагональ куба находится по формуле , где d — диагональ, а — ребро куба.
Тела кубической формы
В форме куба кристаллизуется поваренная соль, флюорит и другие вещества.
Слайд 20Октаэдр
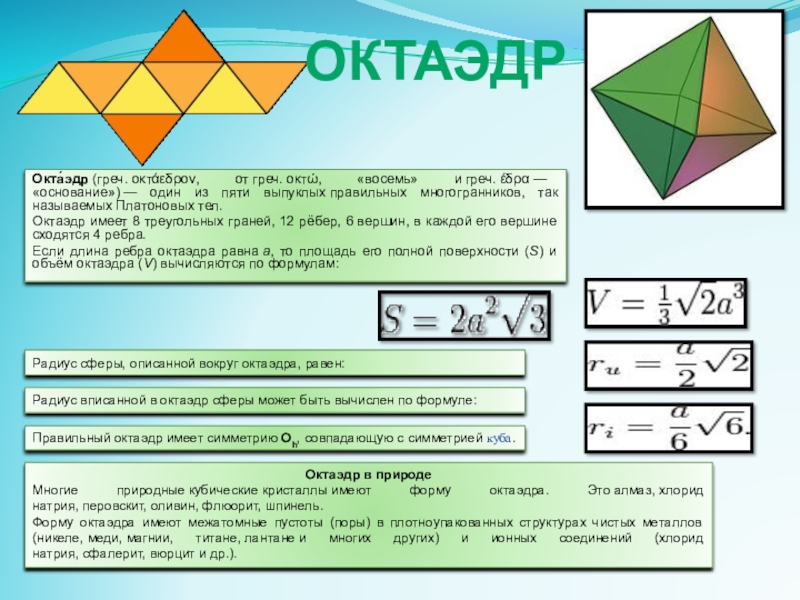
Окта́эдр (греч. οκτάεδρον, от греч. οκτώ, «восемь» и греч. έδρα — «основание») — один из пяти выпуклых правильных многогранников, так
Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
Если длина ребра октаэдра равна а, то площадь его полной поверхности (S) и объём октаэдра (V) вычисляются по формулам:
Радиус сферы, описанной вокруг октаэдра, равен:
Радиус вписанной в октаэдр сферы может быть вычислен по формуле:
Правильный октаэдр имеет симметрию Oh, совпадающую с симметрией куба.
Октаэдр в природе
Многие природные кубические кристаллы имеют форму октаэдра. Это алмаз, хлорид натрия, перовскит, оливин, флюорит, шпинель.
Форму октаэдра имеют межатомные пустоты (поры) в плотноупакованных структурах чистых металлов (никеле, меди, магнии, титане, лантане и многих других) и ионных соединений (хлорид натрия, сфалерит, вюрцит и др.).
Слайд 21Додекаэдр
Додека́эдр (от греч. δώδεκα — двенадцать и εδρον — грань), двенадцатигранник —правильный многогранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра
Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра). Сумма плоских углов при каждой из 20 вершин равна 324°.
Додекаэдр имеет 3 звёздчатые формы.
С древнейших времён известна фигура, у которой 12 граней — правильные пятиугольники. Такой додекаэдр — одно из пяти платоновых тел и обладает симметрией вращения пятого порядка. Однако, у этого во многих отношениях идеального многогранника есть недостаток. Дело в том, что правильными пятиугольниками нельзя без зазоров покрыть плоскость. Также додекаэдрами невозможно плотно заполнить пространство. Из этого следует невозможность существования кристаллов с осями симметрии пятого порядка и невозможность существования кристаллов в форме платоновского додекаэдра. Однако, известны вирусы и белки́ в форме такого додекаэдра, с осями симметрии пятого порядка. Предполагают, что они приобрели такую форму во избежание кристаллизации.
Слайд 22Основные формулы
Если за длину ребра принять a, то площадь поверхности додекаэдра:
Объем додекаэдра:
Радиус
Радиус вписанной сферы:
Элементы симметрии додекаэдра
Додекаэдр имеет центр симметрии и 15 осей симметрии.
Каждая из осей проходит через середины противолежащих параллельных ребер.
Додекаэдр имеет 15 плоскостей симметрии. Любая из плоскостей симметрии проходит в каждой грани через вершину и середину противоположного ребра.
Тела в форме додекаэдра
Додекаэдр применяется как генератор случайных чисел (вместе с другими костями) в настольных ролевых играх, и обозначается при этом d12(dice — кости).
В игре Пентакор мир представлен в виде этой геометрической фигуры.
Слайд 23Пентагондодекаэдр
Визуально очень похож на платоновское тело, но имеет совсем другую симметрию — центральный
Ромбододекаэдр
Фигура, огранённая ромбами.
Между пентагондодекадэром и ромбододекаэдром существует непосредственная связь. Петагондодекаэдр получается из ромбододекаэдра, если отклонить грань ромбододекаэдра в сторону вершины. В этом смысле, пентагондодекаэдр является переходной формой между кубом и ромбододекаэдром.
Слайд 24Икосаэдр
Икоса́эдр (от греч. εικοσάς — двадцать; -εδρον — грань, лицо, основание) — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел.
Площадь S, объём V икосаэдра с длиной ребра a, а также радиусы вписанной и описанной сфер вычисляются по формулам:
Свойства
Икосаэдр можно вписать в куб, при этом, шесть взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба
В икосаэдр может быть вписан тетраэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Икосаэдр можно вписать в додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра.
В икосаэдр можно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра.
Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12×5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12×5=90.
Слайд 25Усечённый икосаэдр
Усечённый икосаэдр - многогранник, состоящий из 12 правильных пятиугольников и 20
В мире
Икосаэдр лучше всего из всех правильных многогранников подходит для триангуляции сферы методом рекурсивного разбиения. Поскольку он содержит наибольшее среди них количество граней, искажение получающихся треугольников по отношению к правильным минимально.
Икосаэдр применяется как игральная кость в настольных ролевых играх, и обозначается при этом d20 (dice — кости).
Тела
Капсиды многих вирусов (например, бактериофаги, мимивирус).