- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Методическая разработка урока по геометрии
Содержание
- 1. Методическая разработка урока по геометрии
- 2. Тела вращения
- 3. оглавление1.Виды тел вращения 2.Определения тел вращения: а)цилиндр б)конус в)шар
- 4. ВИДЫ ТЕЛ ВРАЩЕНИЯЦилиндр-тело, которое описывает прямоугольник при
- 5. ОПРЕДЕЛЕНИЕ ЦИЛИНДРАЦилиндром называется тело, которое состоит из
- 6. ОПРЕДЕЛЕНИЕ КОНУСАКонусом называется тело,которое состоит из круга-основания
- 7. ОПРЕДЕЛЕНИЕ ШАРАШаром называется тело, которое состоит из
- 8. ОПРЕДЕЛЕНИЕ УСЕЧЕННОГО КОНУСАУсеченным
- 9. Объемы и площади тел вращения
- 10. Геометрическое тело: конус Дано: R=1м, Н=2м,
- 11. Геометрическое тело: ЦилиндрДано: Н=3м, R=2м.
- 12. Геометрическое тело: шар Дано: R=5м Найти:
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
Слайд 3оглавление
1.Виды тел вращения
2.Определения тел вращения:
а)цилиндр
б)конус
в)шар
г)
3.Объёмы и площади тел
вращения
4.Задачи
Завершить работу
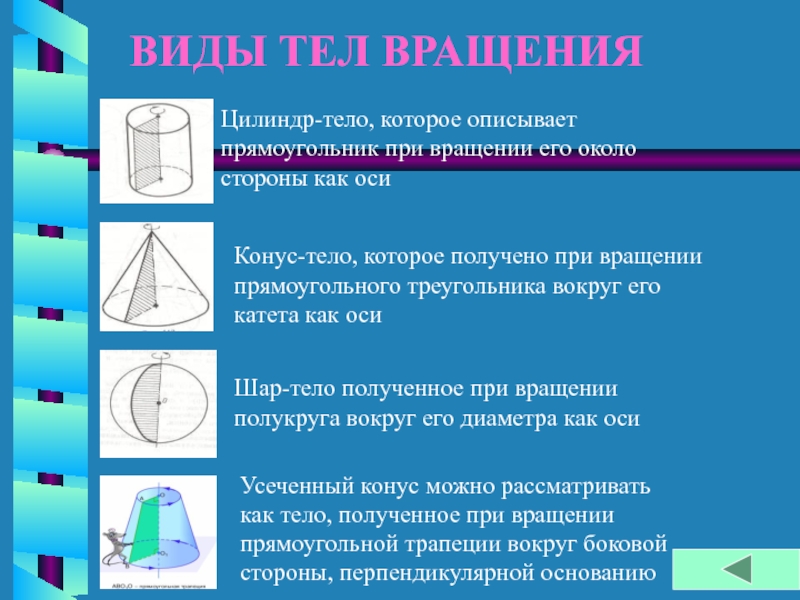
Слайд 4ВИДЫ ТЕЛ ВРАЩЕНИЯ
Цилиндр-тело, которое описывает прямоугольник при вращении его около стороны
Конус-тело, которое получено при вращении прямоугольного треугольника вокруг его катета как оси
Шар-тело полученное при вращении полукруга вокруг его диаметра как оси
Усеченный конус можно рассматривать как тело, полученное при вращении прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию
Слайд 5ОПРЕДЕЛЕНИЕ ЦИЛИНДРА
Цилиндром называется тело, которое состоит из двух кругов, не лежащих
Круги называются основаниями цилиндра, а отрезки,соединяющие соответствующие точки окружностей кругов,образующими цилиндра.
Слайд 6ОПРЕДЕЛЕНИЕ КОНУСА
Конусом называется тело,которое состоит из круга-основания конуса,точки, не лежащей в
Слайд 7ОПРЕДЕЛЕНИЕ ШАРА
Шаром называется тело, которое состоит из всех точек пространства, находящихся
Слайд 8
ОПРЕДЕЛЕНИЕ УСЕЧЕННОГО КОНУСА
Усеченным конусом называется часть полного конуса, заключенная между основанием
Слайд 10Геометрическое тело:
конус
Дано: R=1м, Н=2м,
L=3м
Найти: К
Решение:
1) Найдем
S=Sб+Sосн
S=πRL +πR2= 12,56м2
2) Найдем объем:
V=1/3πR2H=2,09м3
3) К =(36πV2)/S3=0,25<1
Слайд 11Геометрическое тело:
Цилиндр
Дано: Н=3м, R=2м.
Найти :К
Решение:
1) Найдем полную
2)Найдем объем:
V= Sосн.* Н=πR2*Н V=3.14*4*3=37,68м3
3) К =36πV2/S3= 160492,2/247673,15= 0,65<1
Слайд 12Геометрическое тело:
шар
Дано: R=5м
Найти: К
Решение
1)Найдем площадь поверхности шара:
S=4
2)Найдем объем шара:
V = 4/3 π R3= =4/3*3. 14*125=523.3м3
3)K=36π V2 /S 3 = 36*3,14*273529/30959 144=0,9989 ≈1