- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Методическая разработка раздела общеобразовательной программы по геометрии 8 класс
Содержание
- 1. Методическая разработка раздела общеобразовательной программы по геометрии 8 класс
- 2. Урок 1. Площадь многоугольникаЦели урока: Дать представление
- 3. Решить задачи№1. Через точку во внутренней области
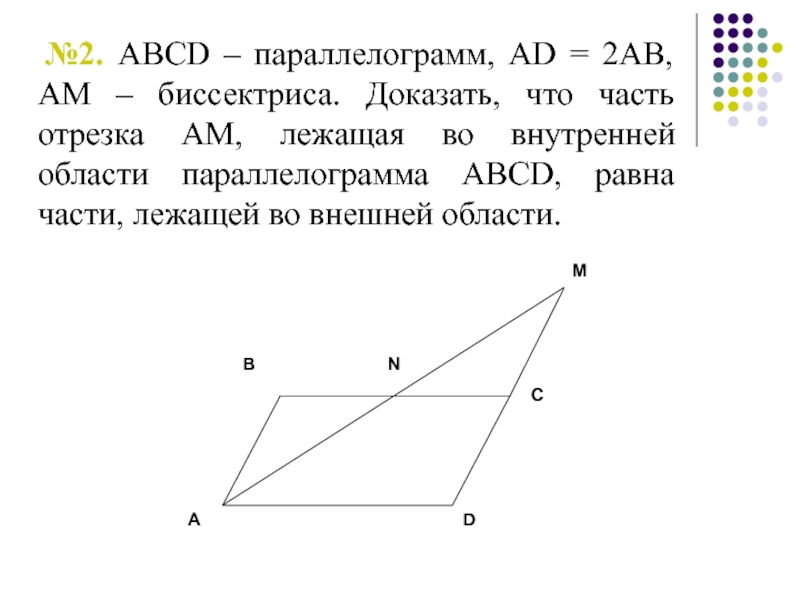
- 4. №2. ABCD – параллелограмм, AD
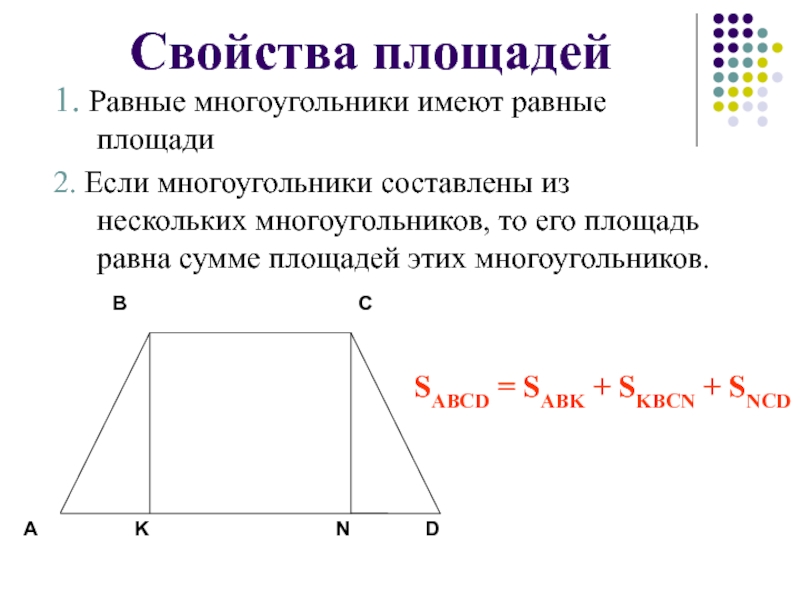
- 5. Свойства площадей1. Равные многоугольники имеют равные площади2.
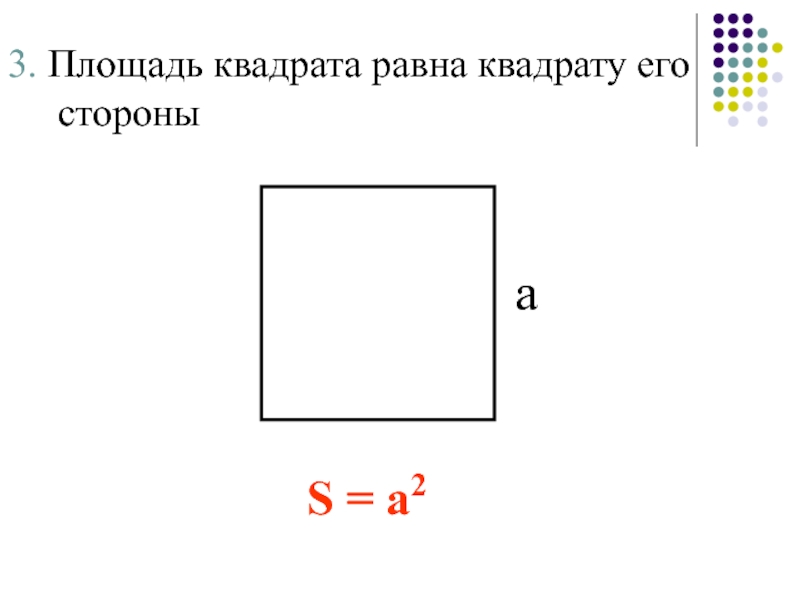
- 6. 3. Площадь квадрата равна квадрату его стороны S = а2а
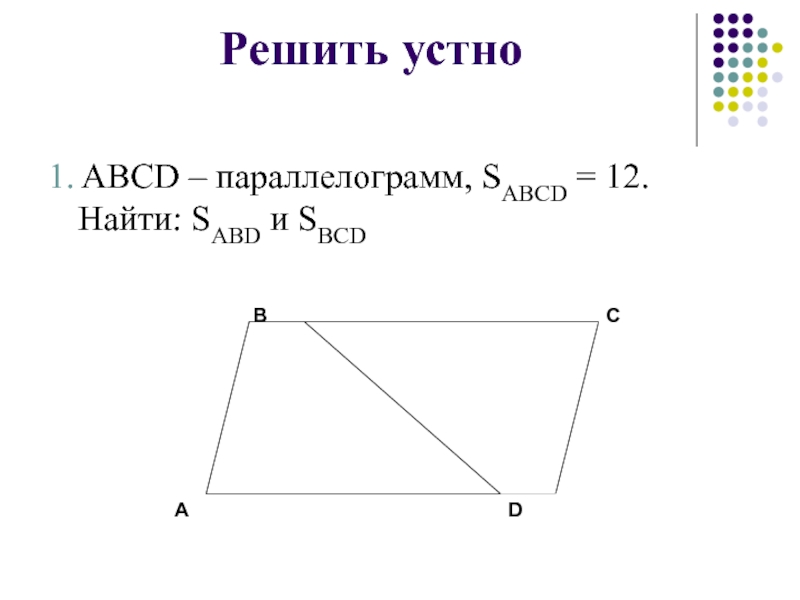
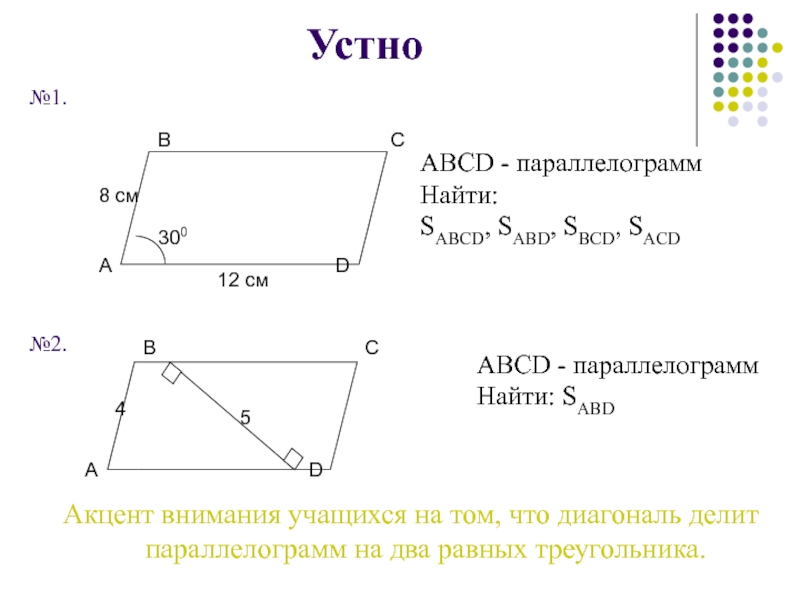
- 7. Решить устно1. ABCD – параллелограмм, SABCD = 12. Найти: SABD и SBCD
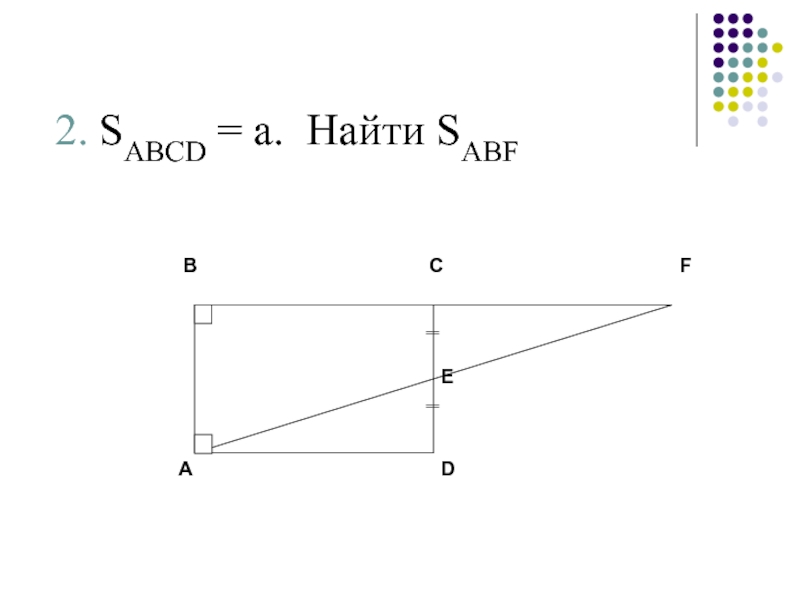
- 8. 2. SABCD = а. Найти SABF
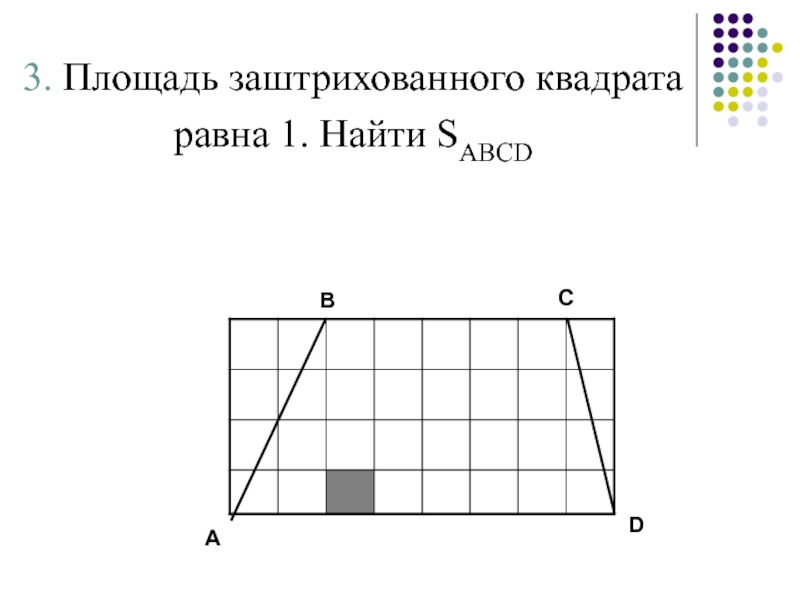
- 9. 3. Площадь заштрихованного квадрата равна 1. Найти SABCD АВ СD
- 10. 4. Площадь заштрихованного квадрата равна 1. Найти SABFАBF
- 11. Домашнее задание П.48, п.49; вопросы 1,2; № 448, №449 (б), № 450 (б), № 446.
- 12. Урок 2. Площадь прямоугольникаЦели урока: Вывести формулу
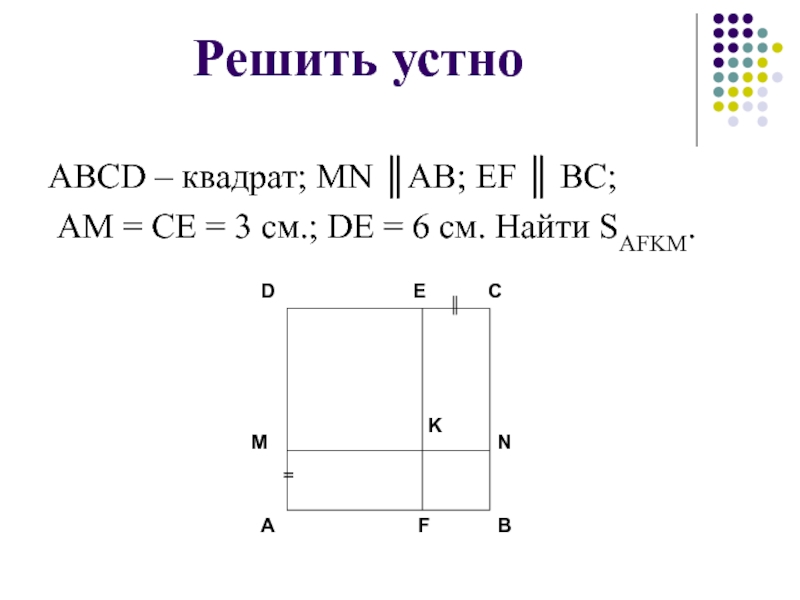
- 13. Решить устноABCD – квадрат; MN ║AB; EF
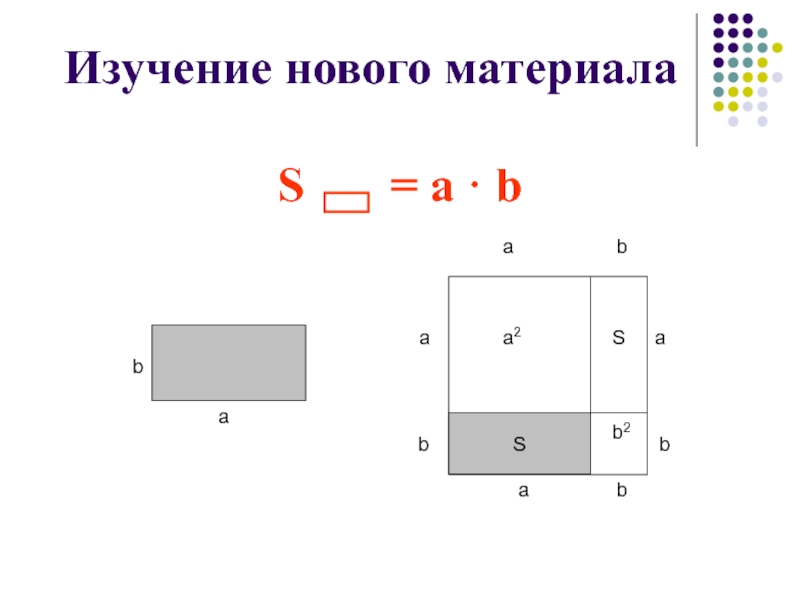
- 14. Изучение нового материалаS = а · b
- 15. Самостоятельная работа I уровень№1. Найти площадь прямоугольника,
- 16. II уровень№1. Площадь квадрата равна 64 см.2
- 17. №1. Периметр прямоугольника равен 26 см., а
- 18. СамопроверкаI уровень№1. Р = 2х + 3х
- 19. №2. Р = 96 см.1). АВ =
- 20. II уровень№1.SABCD = 64 см2 АВ =
- 21. №2. SABCD = SMDKP = 64 см2SACКМ
- 22. III уровень№1. Р = 26 см(х +
- 23. №2.SABCD = 16 · 10 =160 (
- 24. Домашнее задание П.50; № 454, №455, № 456, в рабочих тетрадях № 32.
- 25. Урок 3. Площадь параллелограмма Цели урока:1. Вывести
- 26. Устно№1. Дано: ABCD – параллелограмм, BM =
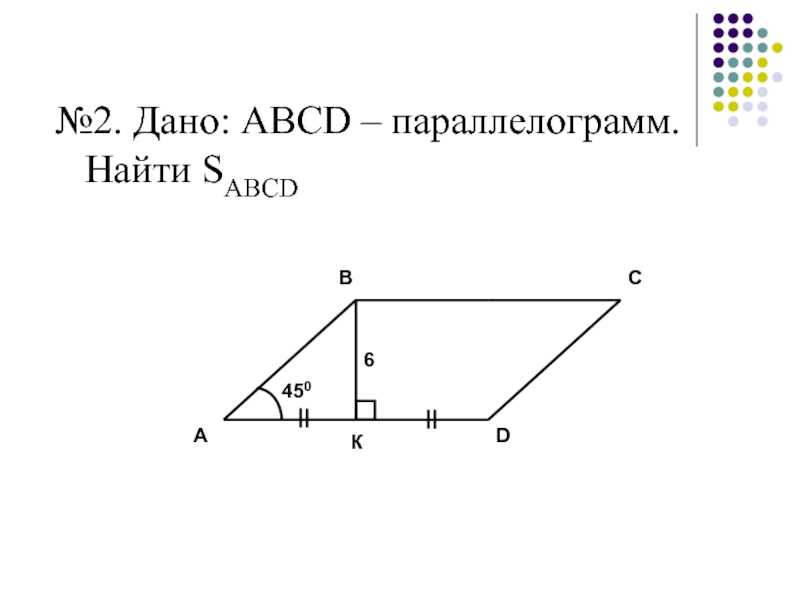
- 27. №2. Дано: ABCD – параллелограмм. Найти SABCD
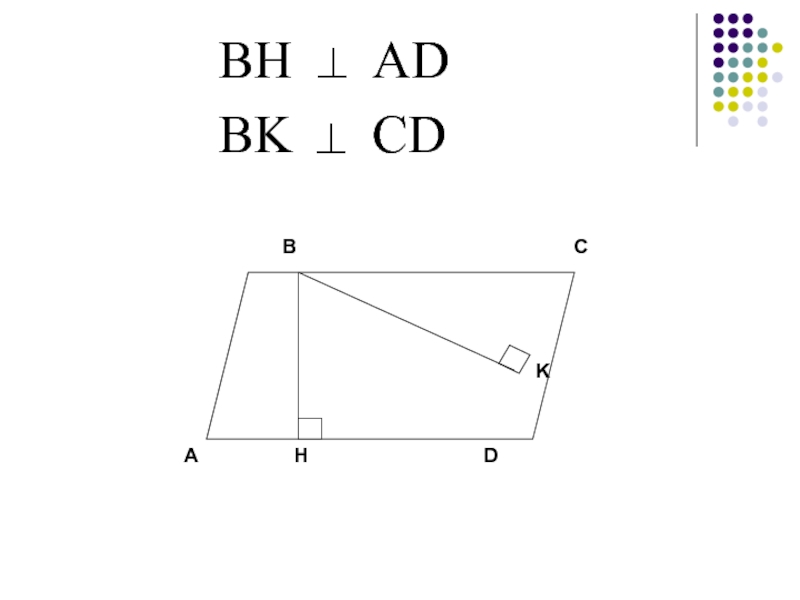
- 28. ВН ADBK CD
- 29. ЗадачаДано ABCD – параллелограмм, AD = а,
- 30. № 464 (в)Площадь параллелограмма равна 54 см2,
- 31. Дополнительные задачиSABCD = ?Ответ: 24 см2MNPК –
- 32. Домашнее заданиеп.51, в.4; № 459 (в, г), № 460, № 462.
- 33. Урок 4. Площадь треугольникаЦели урока: Вывести формулу
- 34. Устно№1.№2.№3.SABCD = ?SMNPТ = ?SABCD = ?
- 35. Устно№1.№2.Акцент внимания учащихся на том, что диагональ
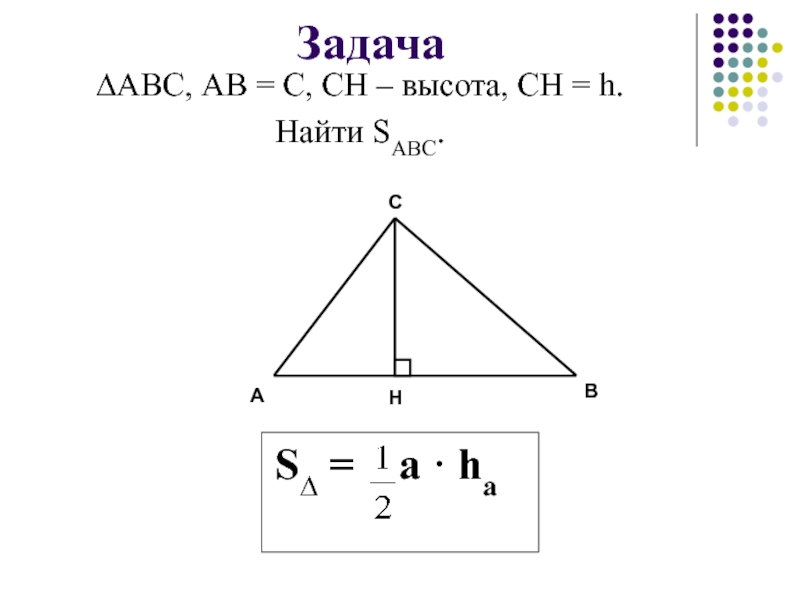
- 36. Задача ∆АВС, АВ = С, СН –
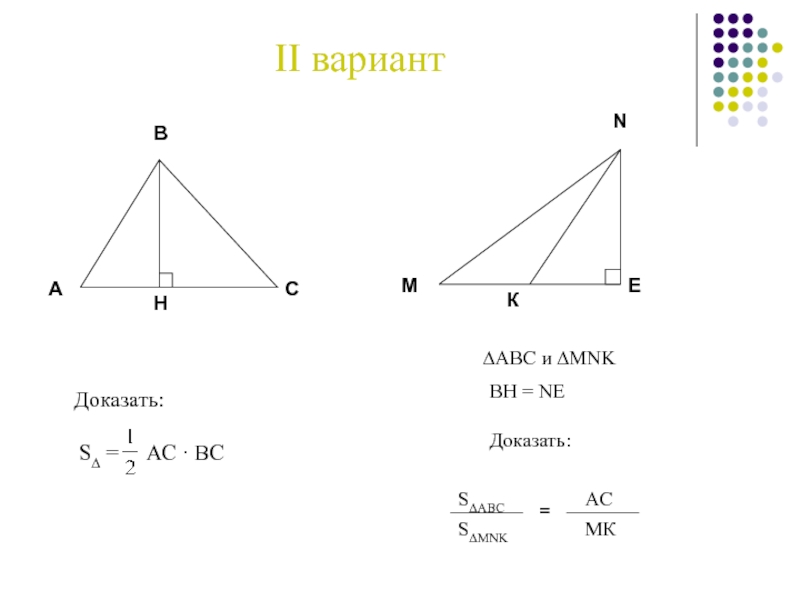
- 37. Самостоятельная работаI вариантДоказать: S∆ = АС · ВС
- 38. II вариант∆АВС и ∆MNKВН = NЕДоказать:
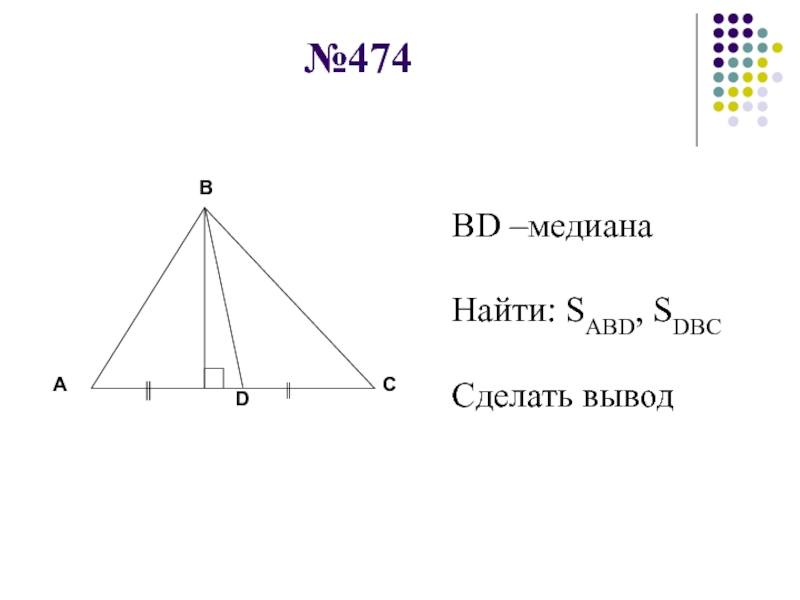
- 39. №474BD –медианаНайти: SABD, SDВССделать вывод
- 40. Домашнее заданиеп.52; № 468 (в, г), № 473, № 469.
- 41. Урок 5. Площадь треугольникаЦели урока: Рассмотреть теорему
- 42. Тест (с последующей проверкой)1.Найти: SABСОтветы: 1). 72
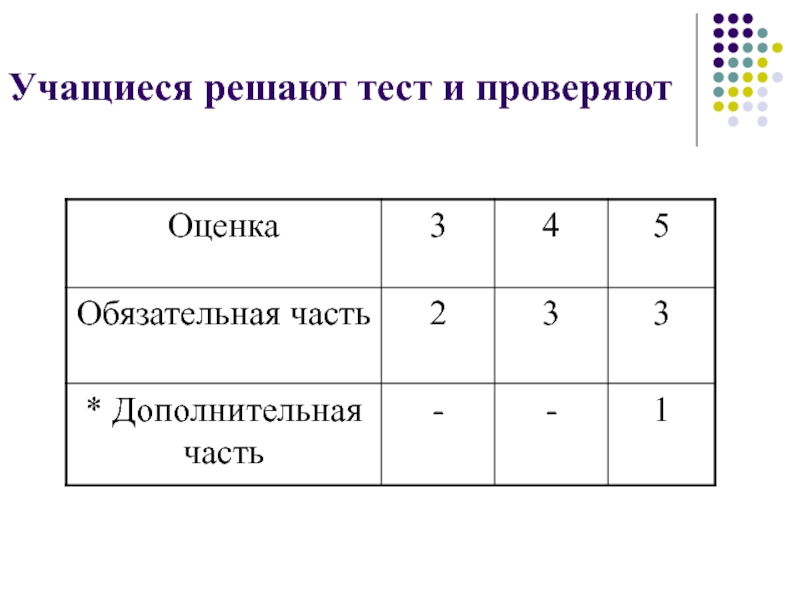
- 43. Учащиеся решают тест и проверяют
- 44. Дано:
- 45. Слайд 45
- 46. · 4,5
- 47. Домашнее заданиеп.52, в.6; № 479 (а), № 477, № 476 (а).
- 48. Урок 6. Площадь трапецииЦели урока: Рассмотреть теорему
- 49. Решение задачи с целью подготовки учащегося к
- 50. Sтрапеции = (а + b) · hа, b – основания трапеции,h - высота
- 51. Основания равнобедренной трапеции 12 см и
- 52. Домашнее задание№ 480 (б), № 481, №
- 53. Урок 7. Решение задач на вычисление площадей
- 54. Слайд 54
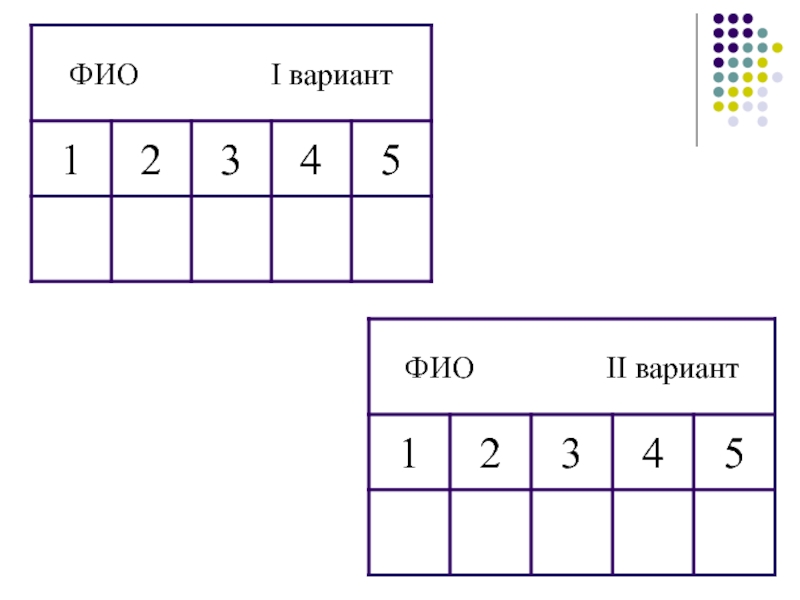
- 55. I вариант:1. Выбери верное утверждение:
- 56. II вариант.1. Выбери верное утверждение:
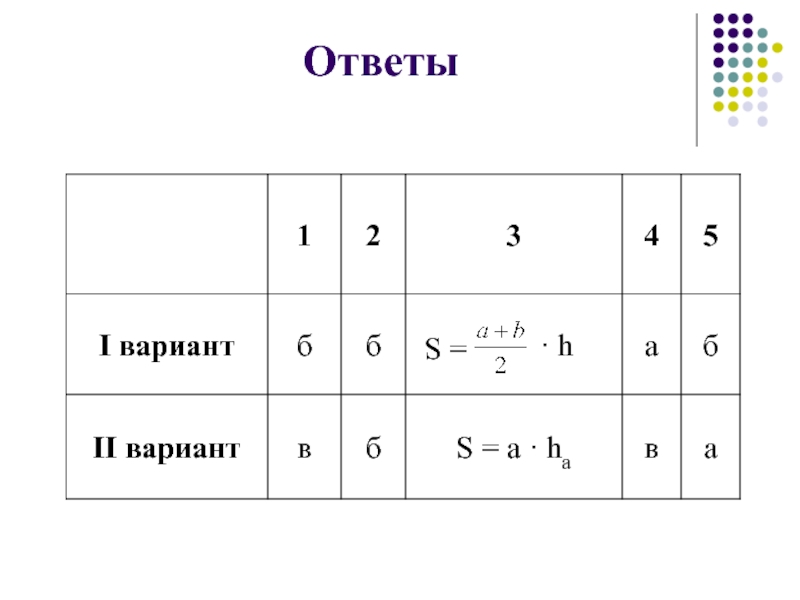
- 57. ОтветыS =
- 58. Домашнее задание№466, № 467, № 476 (б).
- 59. Урок 8. Решение задач на вычисление площадей
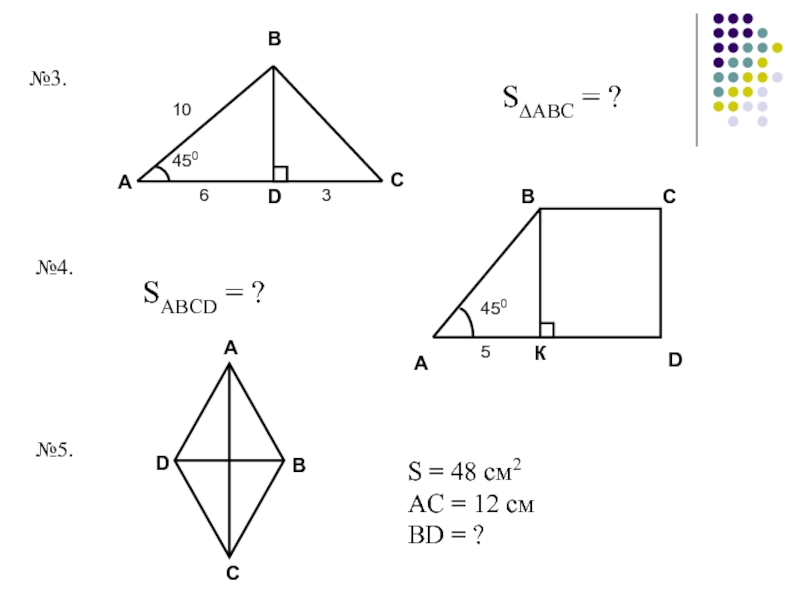
- 60. Решение задач по готовым чертежам ВК = ?№1.№2.S∆ABC = ?
- 61. №3.№4.№5.S∆ABC = ?SABCD = ?S = 48 см2АC = 12 смBD = ?
- 62. Самостоятельная работаК задачам №1 и №2 начертите
- 63. II вариант.№1. Сторона параллелограмма равна 17 см,
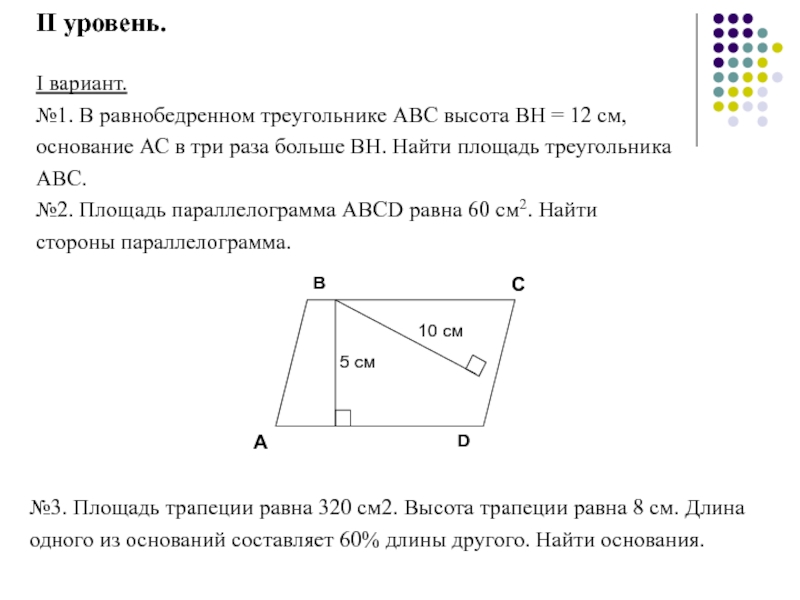
- 64. II уровень.I вариант.№1. В равнобедренном треугольнике АВС
- 65. II вариант.№1. В равнобедренном треугольнике АВС высота
- 66. CамопроверкаI уровеньI вариант№1. S = 21
- 67. S =
- 68. АС = 36 см.S∆ =
- 69. №3. ВН = 6 смКМ = 6
- 70. Урок 9. Теорема ПифагораЦель урока: Рассмотреть теорему Пифагора и показать её применение в ходе решения задач.
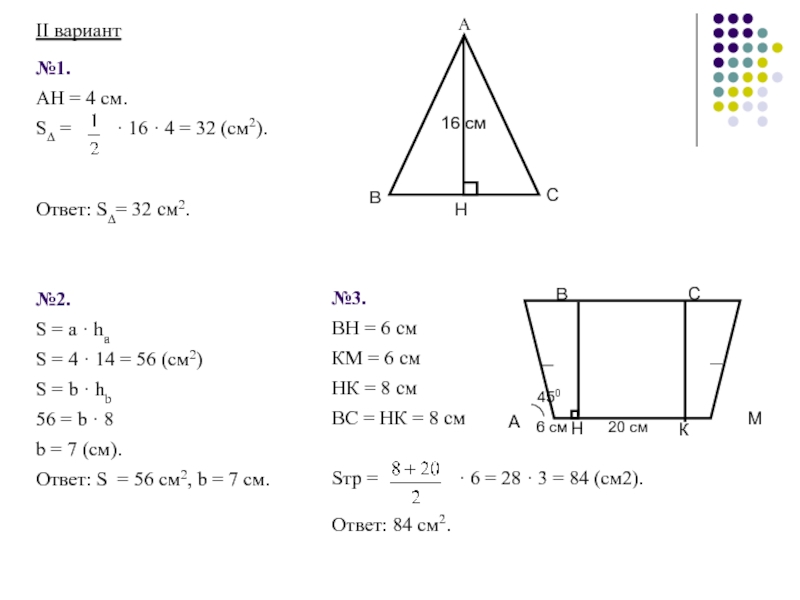
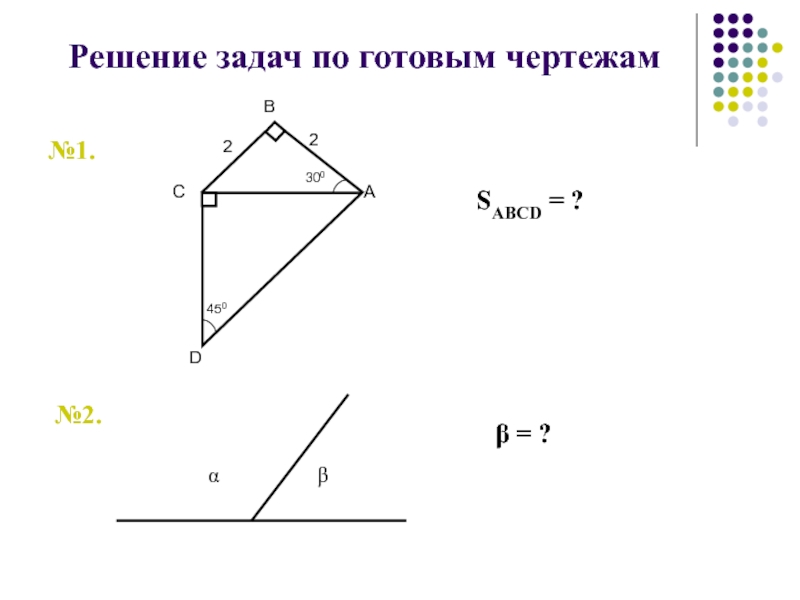
- 71. Решение задач по готовым чертежамSABCD = ?№1.№2.β = ?
- 72. №3.№4.β = ?Доказать, что MNPK - квадрат
- 73. Историческая справкаVI век до н.э. – математик
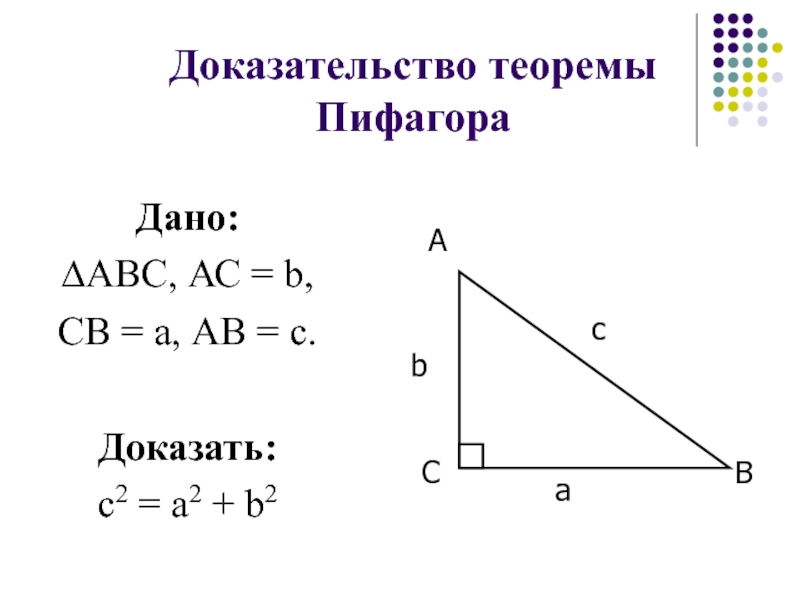
- 74. Доказательство теоремы ПифагораДано: ∆АВС, АС = b,
- 75. Доказательство:а). Достроим квадрат CKPDSCKPD = (а +
- 76. Домашнее заданиеп.54, в.8; № 483 (в, г), № 484 (в, г), № 486 (в).
- 77. Урок 10. Теорема, обратная теореме ПифагораЦели урока:
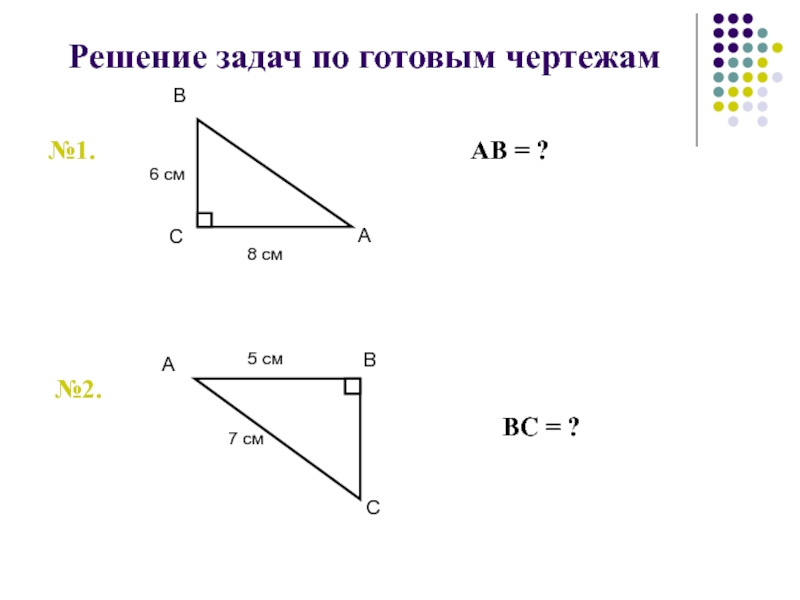
- 78. Решение задач по готовым чертежам№1.№2.АВ = ?ВС = ?
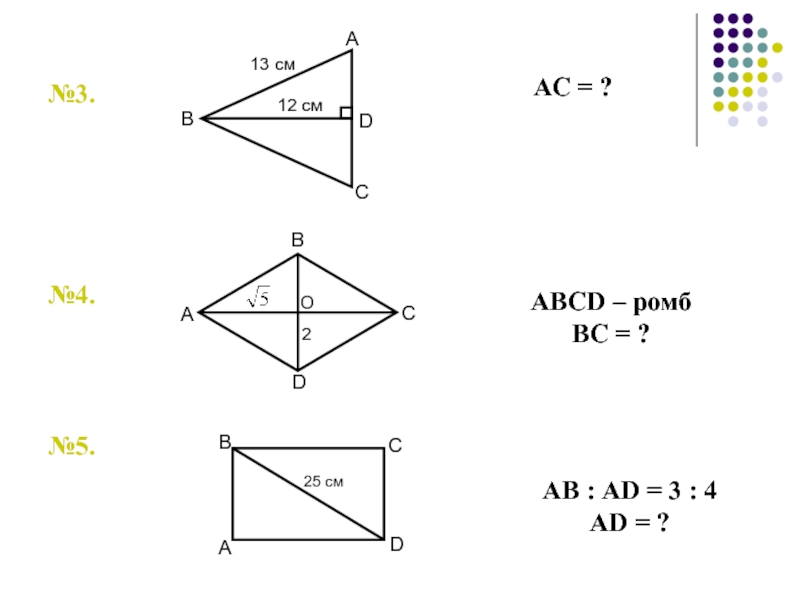
- 79. АС = ?№3.№4.№5.АВСD – ромбВС = ?АВ : АD = 3 : 4АD = ?
- 80. Домашнее заданиеп.55, № 498 (г, д, е), № 499(б), № 488, задачу №49 из рабочей тетради.
- 81. Урок 11. Решение задач по теме «теорема
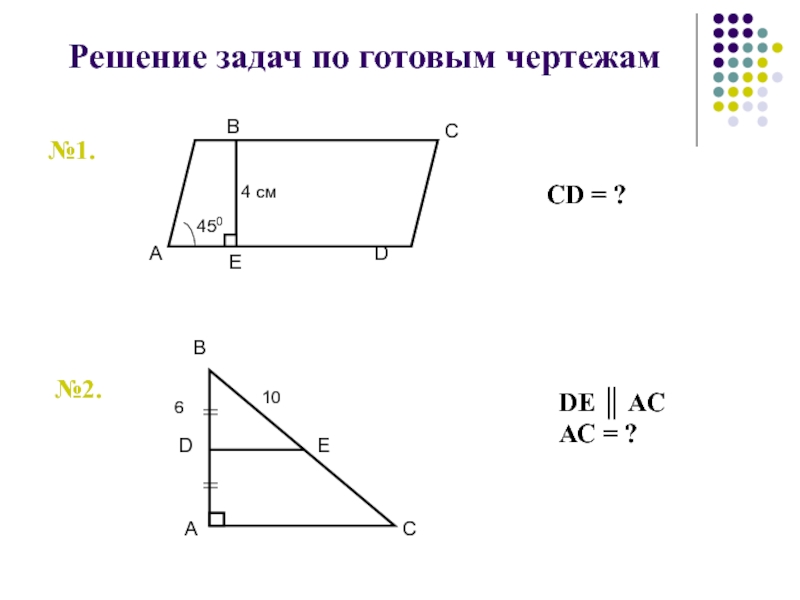
- 82. Решение задач по готовым чертежам№1.№2.СD = ?DE ║ АСАС = ?
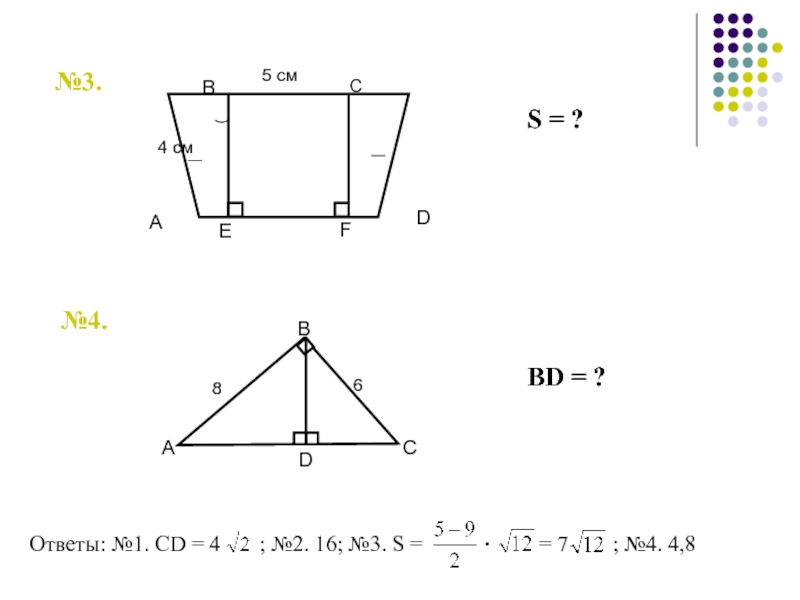
- 83. №3.№4.S = ?ВD = ? · Ответы:
- 84. На «3»I вариант1. Стороны прямоугольника равны 8
- 85. На «4»II вариант1. В прямоугольной трапеции меньшие
- 86. На «5»III вариант1. В ∆АВС АВ =
- 87. Домашнее задание№ 489 (а, в), № 493.
- 88. Урок 12. Решение задачЦели урока:Закрепить знания, умения, навыки учащихся по теме «Площадь».Совершенствовать навыки решения задач.
- 89. Ответы и указания к задачам самостоятельной работыI
- 90. Ответ: 24 см2.II вариант.№1. 1).
- 91. III вариант.№1. АВ2 = ВМ2 + АМ2
- 92. Домашнее задание№ 495 (в), № 490. На
- 93. Урок 13. Решение задачЦели урока:Совершенствовать навыки решения
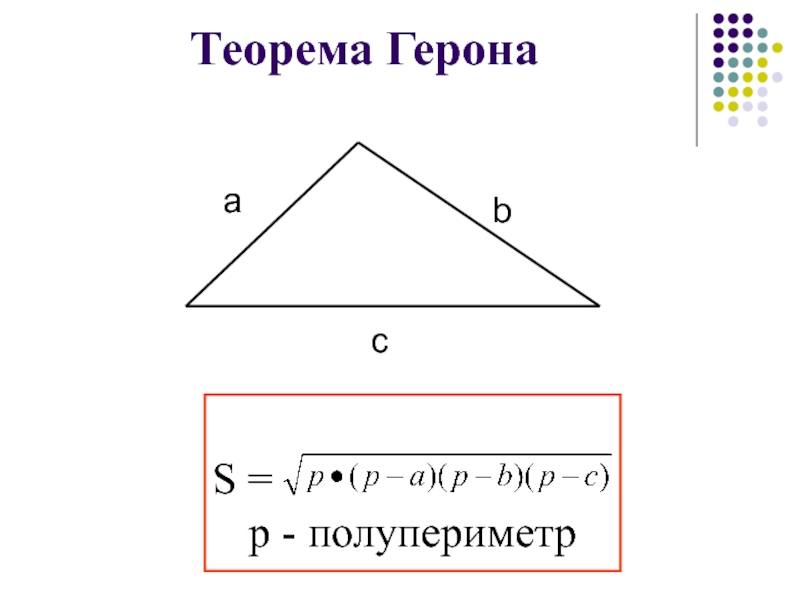
- 94. Теорема ГеронаS = р - полупериметр
- 95. Решение задач по готовым чертежам№1.№2.S = ?S = ?
- 96. Домашнее задание№ 490 (в), № 497, № 503, № 518.
- 97. Контрольная работаI уровеньI вариант№1. Сторона треугольника равна
- 98. II уровеньII вариант№1. Смежные стороны параллелограмма равны
- 99. III уровеньIII вариант№1. На стороне AD параллелограмма
- 100. Дано: ALKC - квадрат, ABCD - квадрат.Доказать:
- 101. I способ. (рис. *) Δ ACD –
- 102. Зачёт №1 по теме «Теорема Пифагора» Билеты
- 103. Контрольная работаS∆АВС = ?В1ВСD – квадрат,SВ1ВСD = 4, ВВ1 = 4, ВВ1 = АВ1Найти: АВ2№1.№2.
- 104. №3.№4.№5.S∆АВС = ?SАВDЕ = 100 см2АС =
- 105. Зачёт №2 по теме «Теорема Пифагора» Тест
- 106. Дополнительная часть7). (4) Радиус окружности, описанной около
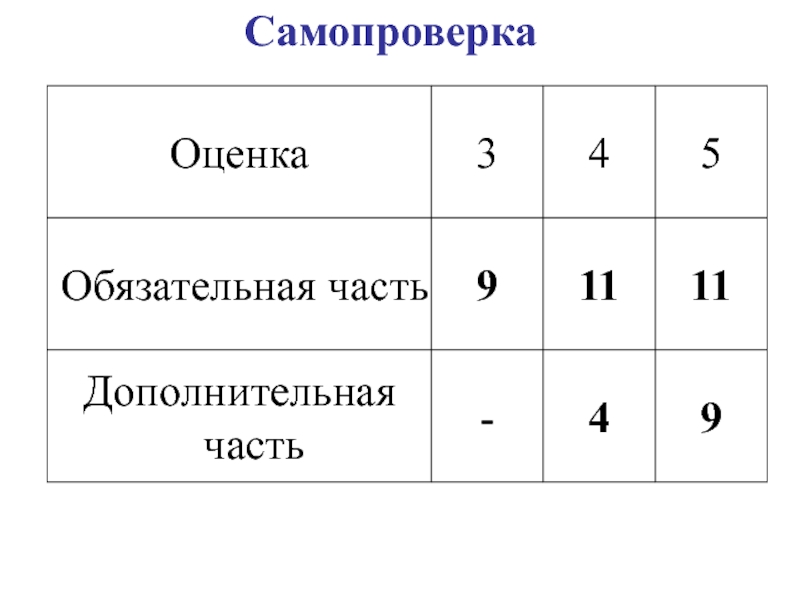
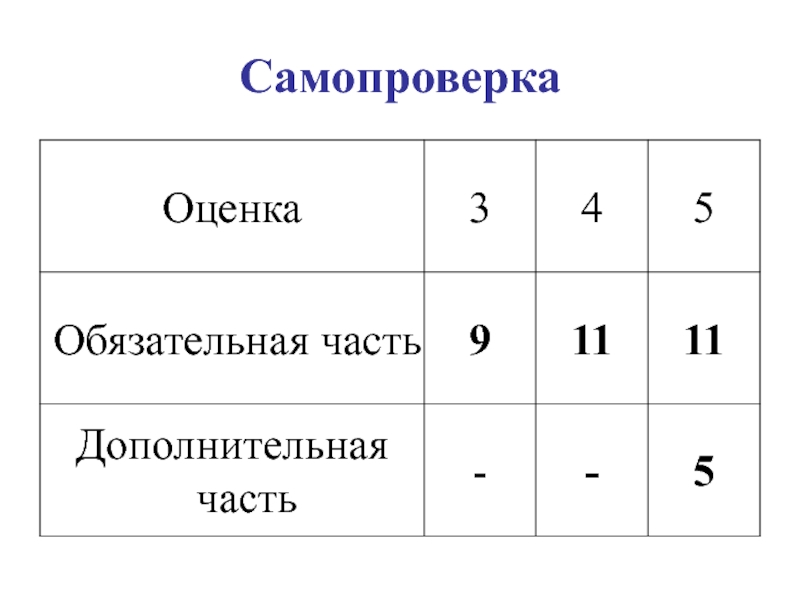
- 107. Самопроверка
- 108. Тест 2. Обязательная часть1). (1) Вставьте пропущенные
- 109. Дополнительная часть6). (3) Найти АD.
- 110. Самопроверка
- 111. Заключение
- 112. Список литературы1. Изучение геометрии в 7 –
Слайд 1Методическая разработка раздела общеобразовательной программы по геометрии
8 класс
Площадь
Автор разработки:
учитель
Слайд 2Урок 1. Площадь многоугольника
Цели урока:
Дать представление об измерении площадей многоугольников.
Рассмотреть
Вывести формулу для вычисления площади квадрата.
Показать учащимся примеры использования изученного теоретического материала в ходе решения задач.
Слайд 3Решить задачи
№1. Через точку во внутренней области равностороннего треугольника проведены две
Слайд 4 №2. ABCD – параллелограмм, AD = 2AB, АМ –
Слайд 5Свойства площадей
1. Равные многоугольники имеют равные площади
2. Если многоугольники составлены из
SABCD = SABK + SKBCN + SNCD
Слайд 12Урок 2. Площадь прямоугольника
Цели урока:
Вывести формулу площади прямоугольника и показать
Совершенствовать навыки решения задач.
Слайд 15Самостоятельная работа
I уровень
№1. Найти площадь прямоугольника, если его периметр 160 см.,
№2. Периметр квадрата ABCD равен 96 см. Найти площадь пятиугольника ABCOD.
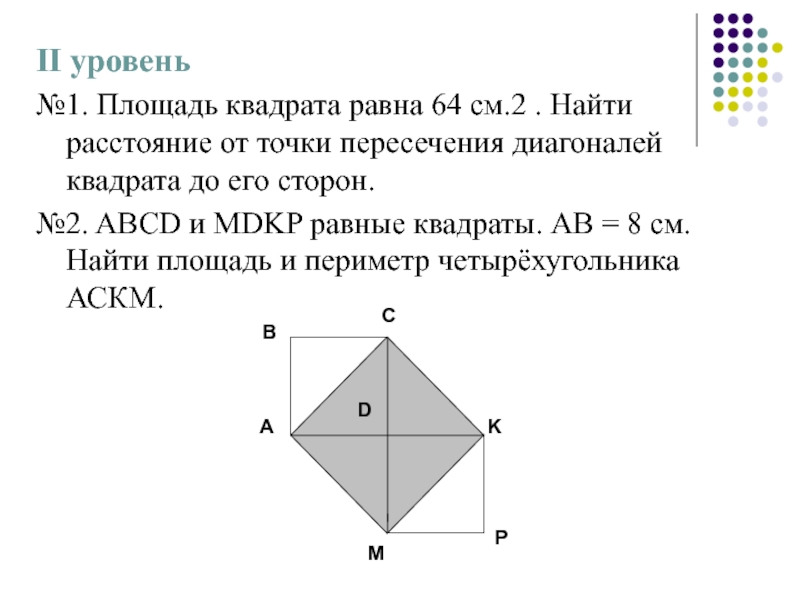
Слайд 16II уровень
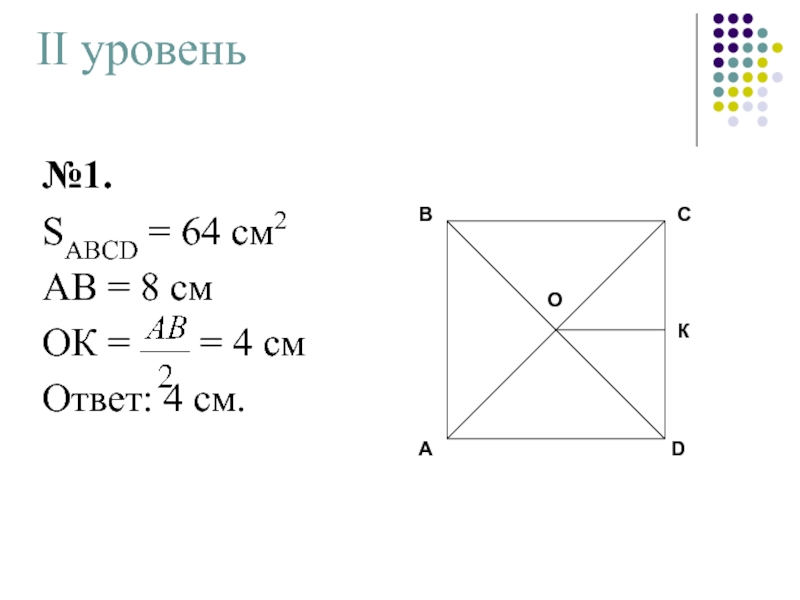
№1. Площадь квадрата равна 64 см.2 . Найти расстояние от
№2. ABCD и MDKP равные квадраты. АВ = 8 см. Найти площадь и периметр четырёхугольника АСКМ.
Слайд 17№1. Периметр прямоугольника равен 26 см., а одна из его сторон
№2. ABCD – прямоугольник. М, К, Р, Т – середины его сторон, АВ =10 см., AD = 16 см. Найти площадь шестиугольника АМКСРТ.
III уровень
Слайд 18Самопроверка
I уровень
№1.
Р = 2х + 3х + 2х + 3х
Р
10х + 160
х = 16
АВ = 32 см., АD = 48 см.
SABCD = 32 · 48 = 1536 (см2)
Ответ: 1536 см2.
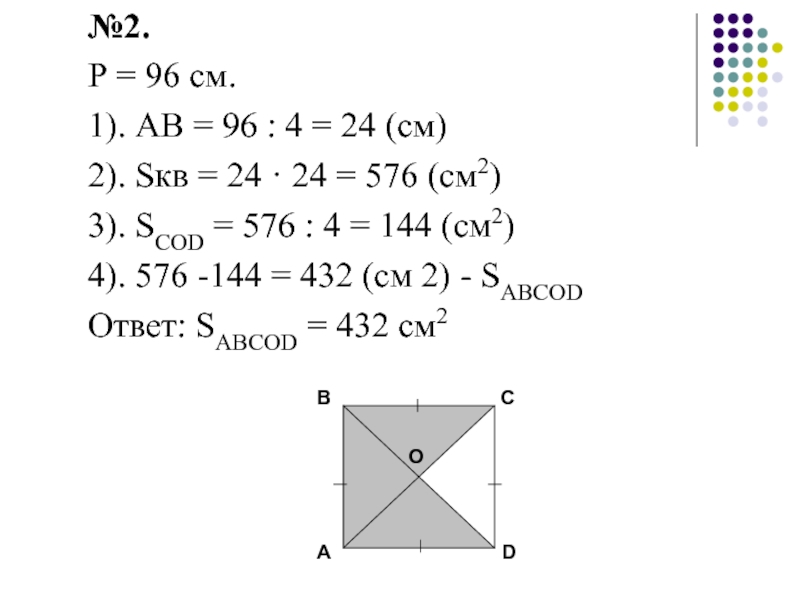
Слайд 19№2.
Р = 96 см.
1). АВ = 96 : 4 =
2). Sкв = 24 · 24 = 576 (см2)
3). SCOD = 576 : 4 = 144 (см2)
4). 576 -144 = 432 (см 2) - SABCOD
Ответ: SABCOD = 432 см2
Слайд 21№2. SABCD = SMDKP = 64 см2
SACКМ = 2 · 64
АС = = 8 (см)
РАСКМ = 8 · 4 = 32 (см)
Ответ: SACКМ = 128 ( см2),
РАСКМ = 32 (см).
Слайд 22III уровень
№1. Р = 26 см
(х + 9)·2 = 26
х +9
х =4
АВ = 4 см, ВС = 9 см.
SABCD = 4 · 9 =36 ( см2)
Sпрямоугольника = Sквадрата
Значит, сторона квадрата 6 см.
Ответ: 6 см.
Слайд 23
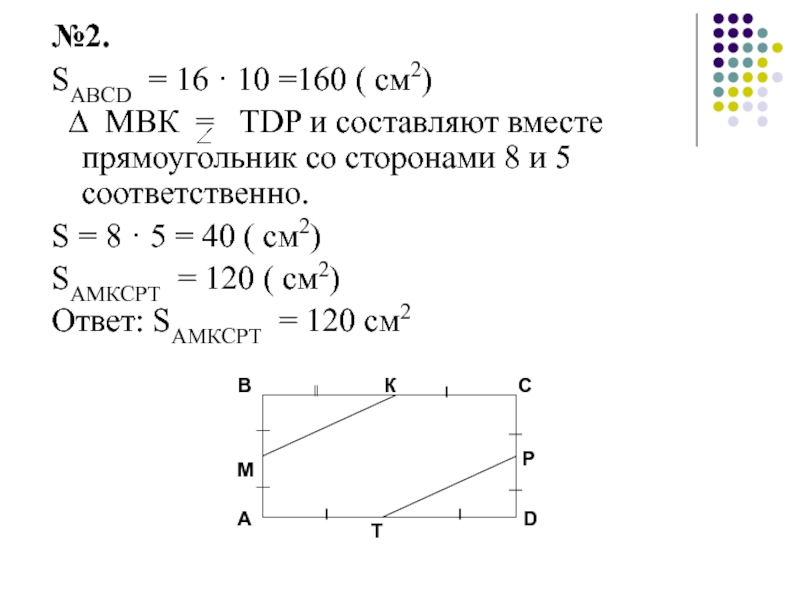
№2.
SABCD = 16 · 10 =160 ( см2)
∆ МВК =
S = 8 · 5 = 40 ( см2)
SАМКСРТ = 120 ( см2)
Ответ: SAМКСРТ = 120 см2
Слайд 25Урок 3. Площадь параллелограмма
Цели урока:
1. Вывести формулу для вычисления площади параллелограмма
2. Совершенствовать навыки решения задач.
Слайд 26Устно
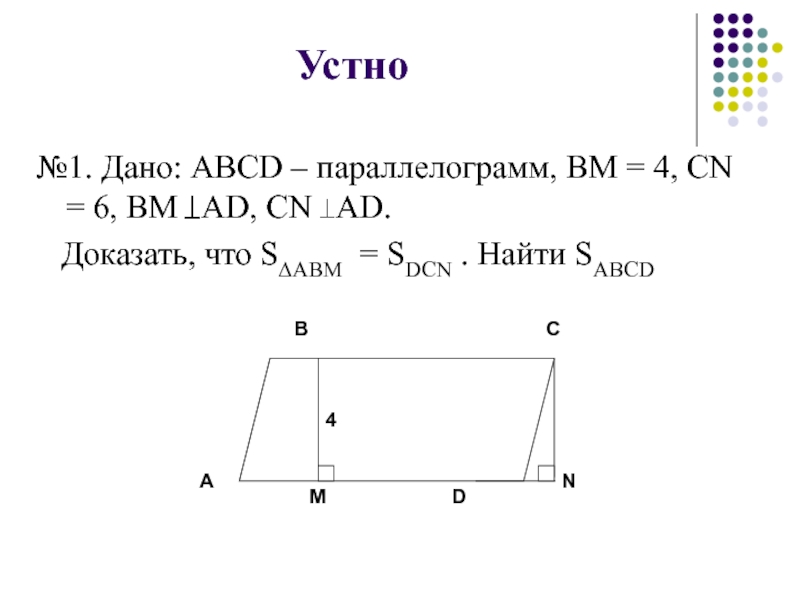
№1. Дано: ABCD – параллелограмм, BM = 4, CN = 6,
Доказать, что S∆АВМ = SDCN . Найти SABCD
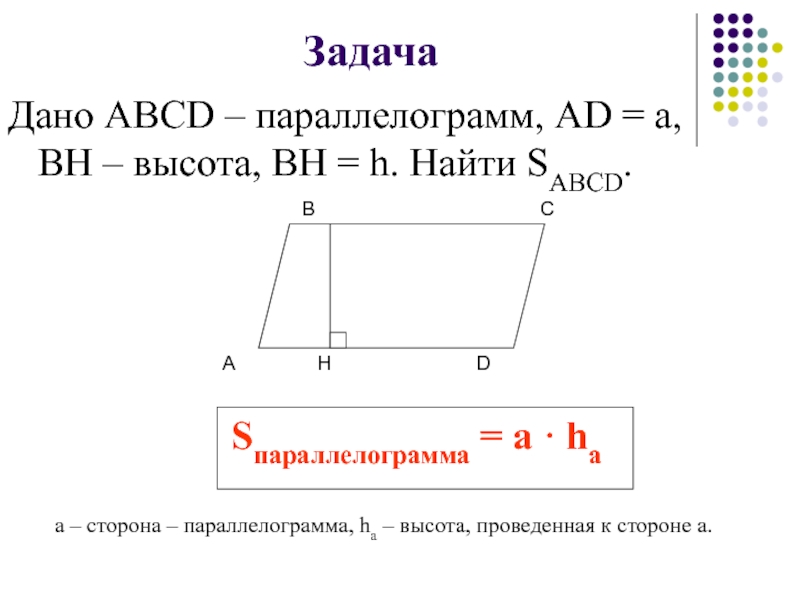
Слайд 29Задача
Дано ABCD – параллелограмм, AD = а, ВН – высота, ВН
Sпараллелограмма = а · hа
а – сторона – параллелограмма, hа – высота, проведенная к стороне а.
Слайд 30№ 464 (в)
Площадь параллелограмма равна 54 см2, а = 4,5 см.,
Sпараллелограмма = а · hа = b · hb
h1 = hа , h2 = hb
h1 = 54 : 6 = 9 (см)
h2 = 54 : 4,5 = 12 (см).
Ответ: h1 = 9 см., h2 = 12 см.
Слайд 31Дополнительные задачи
SABCD = ?
Ответ: 24 см2
MNPК – ромб
МР = 6 см
NК
SMNPК = ?
Ответ: 24 см2
№1.
№2.
Слайд 33Урок 4. Площадь треугольника
Цели урока:
Вывести формулу для вычисления площади треугольника
Совершенствовать навыки решения задач.
Слайд 35Устно
№1.
№2.
Акцент внимания учащихся на том, что диагональ делит параллелограмм на два
ABCD - параллелограмм
Найти:
SABCD, SABD, SBCD, SACD
ABCD - параллелограмм
Найти: SABD
Слайд 41Урок 5. Площадь треугольника
Цели урока:
Рассмотреть теорему об отношении площадей треугольников,
Совершенствовать навыки решения задач.
Слайд 42Тест (с последующей проверкой)
1.
Найти: SABС
Ответы: 1). 72 см2 , 2). 36
2.
Запиши формулу площади параллелограмма по рисунку:
ABCD – квадрат, АВ = 5 см, КD = 4 см. = 4 см. Найти SABСК
Записать ответ _______
3.
Найти: SABС
Ответы: 1). 105 см2 , 2). 60 см2, 3). 30 см2, 4). 120 см2
4*
Слайд 44Дано: =
Решить устно задачи:
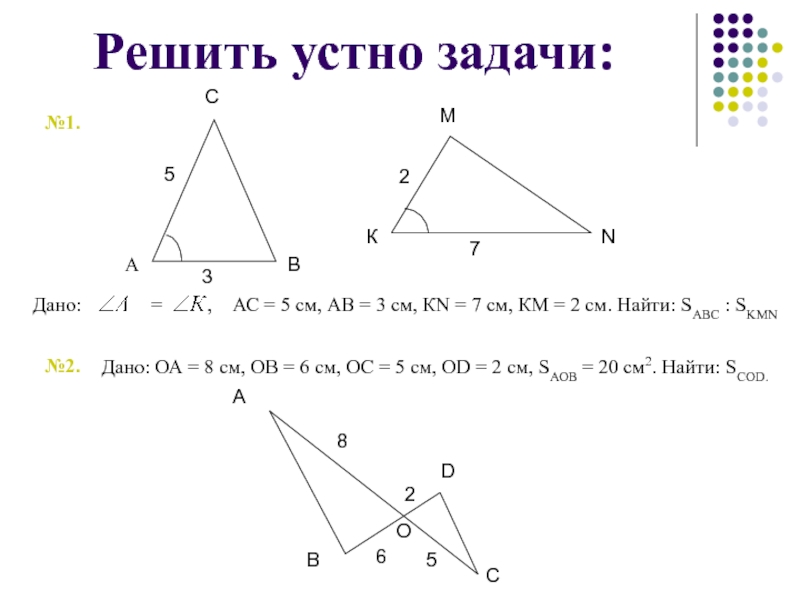
№1.
АС = 5 см, АВ = 3 см, КN = 7 см, КМ = 2 см. Найти: SАВС : SKMN
№2.
Дано: ОА = 8 см, ОВ = 6 см, ОС = 5 см, ОD = 2 см, SАОВ = 20 см2. Найти: SСОD.
Слайд 45
III уровень.
В ∆АВС
= 750,
I уровень.
Две стороны треугольника 12 см и 9 см, а угол между ними 300. Найти площадь треугольника.
II уровень.
В ∆АВС
Самостоятельная работа обучающего характера с последующей самопроверкой
= 300, АВ = 10 см. Найти S∆АВС.
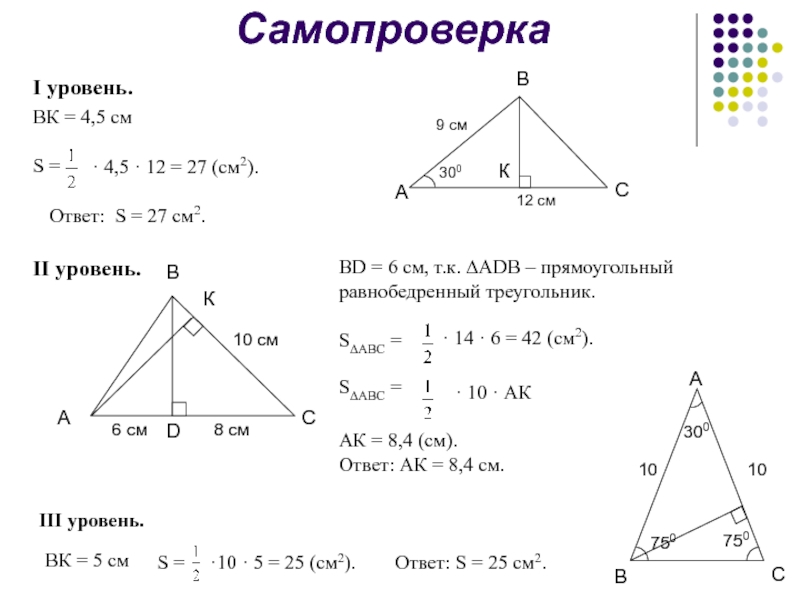
Слайд 46 · 4,5 · 12 = 27
Ответ: S = 27 см2.
Самопроверка
I уровень.
ВК = 4,5 см
S =
II уровень.
ВD = 6 см, т.к. ∆ADB – прямоугольный равнобедренный треугольник.
S∆АВС =
· 14 · 6 = 42 (см2).
S∆АВС =
· 10 · АК
АК = 8,4 (см).
Ответ: АК = 8,4 см.
III уровень.
ВК = 5 см
S = ·10 · 5 = 25 (см2).
Ответ: S = 25 см2.
Слайд 48Урок 6. Площадь трапеции
Цели урока:
Рассмотреть теорему о площади трапеции и
Совершенствовать навыки решения задач.
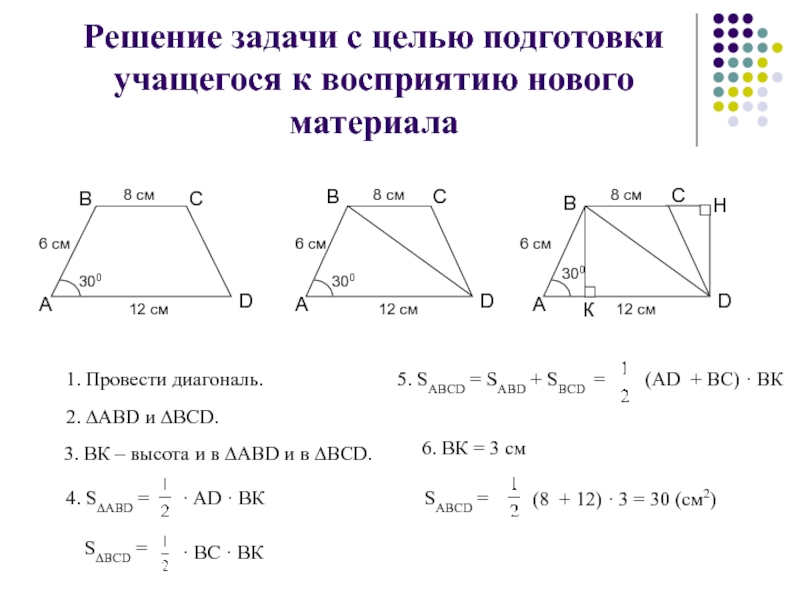
Слайд 49Решение задачи с целью подготовки учащегося к восприятию нового материала
1. Провести
2. ∆ABD и ∆BCD.
3. ВК – высота и в ∆ABD и в ∆BCD.
4. S∆АВD =
· AD · BК
S∆BCD =
· BC · BК
5. SАВСD = SАВD + SВСD =
(AD + ВС) · ВК
6. ВК = 3 см
SАВСD =
(8 + 12) · 3 = 30 (см2)
Слайд 51 Основания равнобедренной трапеции 12 см и 16 см, её диагонали
(ответ: 169 см2).
Решить самостоятельно задачу:
Слайд 52Домашнее задание
№ 480 (б), № 481, № 478.
Повторить формулы для вычисления
Слайд 53Урок 7. Решение задач на вычисление площадей фигур
Цели урока:
Закрепить
Совершенствовать навыки решения задач на вычисление площадей фигур.
Слайд 55I вариант:
1. Выбери верное утверждение:
а). Площадь прямоугольника равна
б). Площадь квадрата равна квадрату его сторон.
в). Площадь прямоугольника равна удвоенному произведению его смежных сторон.
2. S = а · hа - это формула
а). площади прямоугольника,
б). площади параллелограмма,
в). площади ромба.
3. Запиши формулу площади трапеции.
4. ∆АВС и ∆MNК, = Найти отношения площадей ∆АВС и ∆MNК.
а). б). в).
5. В треугольниках MNK и DOS высоты NЕ и ОТ равны.
Тогда SMNК : SPOS = …
а). MN : РО
б). МК : РS
в). NК : ОS
Теоретический тест
Слайд 56II вариант.
1. Выбери верное утверждение:
а). Площадь прямоугольника равна
смежных сторон.
б). Площадь квадрата равна произведению её сторон.
в). Площадь прямоугольника равна произведению двух его сторон.
2. S = d1 · d2 - это формула
а). площади параллелограмма,
б). площади ромба,
в). площади треугольника.
3. Запиши формулу площади параллелограмма.
4. ∆АВС и ∆DEF, = . Найти отношения площадей ∆АВС и ∆DEF.
а). б). в).
5. В треугольниках DEF и TRQ высоты DA и TB равны.
Тогда SDEF : STRQ = …
а). EF : RQ
б). DE : TR
в). EF : RT
Слайд 59Урок 8. Решение задач на вычисление площадей фигур
Цели урока:
Закрепить
Совершенствовать навыки решения задач.
Слайд 62Самостоятельная работа
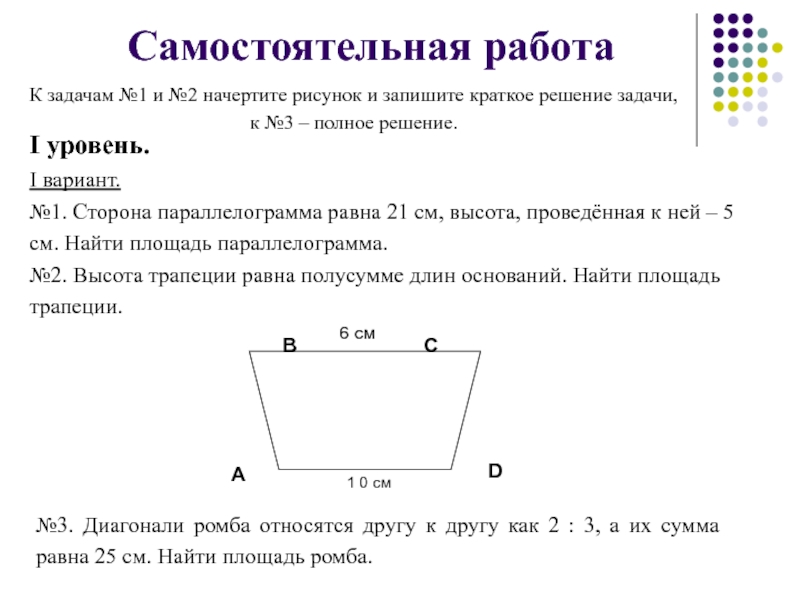
К задачам №1 и №2 начертите рисунок и запишите краткое
к №3 – полное решение.
I уровень.
I вариант.
№1. Сторона параллелограмма равна 21 см, высота, проведённая к ней – 5 см. Найти площадь параллелограмма.
№2. Высота трапеции равна полусумме длин оснований. Найти площадь трапеции.
№3. Диагонали ромба относятся другу к другу как 2 : 3, а их сумма равна 25 см. Найти площадь ромба.
Слайд 63II вариант.
№1. Сторона параллелограмма равна 17 см, его площадь – 187
Найти высоту, проведённую к данной стороне.
№2. Высота трапеции равна полусумме длин оснований. Найти площадь трапеции.
№3. Диагонали ромба относятся другу к другу как 3 : 5, а их сумма равна 8 см. Найти площадь ромба.
Слайд 64II уровень.
I вариант.
№1. В равнобедренном треугольнике АВС высота ВН = 12
№2. Площадь параллелограмма АВСD равна 60 см2. Найти стороны параллелограмма.
№3. Площадь трапеции равна 320 см2. Высота трапеции равна 8 см. Длина одного из оснований составляет 60% длины другого. Найти основания.
Слайд 65II вариант.
№1. В равнобедренном треугольнике АВС высота АН в 4 раза
меньше основания АВ, равного 16 см. Найти площадь треугольника АВС.
№2. Найти площадь параллелограмма и вторую высоту.
№3. В равнобедренной трапеции АВСМ большее основание равно 20 см, высота ВН отсекает от АМ отрезок АН, равный 6 см. Угол ВАМ равен 450. Найти площадь трапеции.
Слайд 66Cамопроверка
I уровень
I вариант
№1.
S = 21 · 15 = 315 (см2).
Ответ:
№2.
h = = 8 см.
S = · h = · 8 = 64 (см2).
Ответ: 64 см2.
№3.
d1 = 2х
d2 = 3
2х + 3х = 25
5х = 25
х = 5
d1 = 10, d2 = 15
Sр = · 10 · 15 = 75 (см2). Ответ: Sр = 75 (см2).
Слайд 67S =
Ответ: 64 см2.
S = · h
№1.
а = = 11 (см).
II вариант
Ответ: 11 см.
№2.
h =
h = = 8 (см)
· 3 · 5 = 7,5 (см2).
Ответ: Sр = 7,5 (см2).
№3.
d1 = 3х
d2 = 5х
3х + 5х = 8
х = 1
d1 = 1, d2 = 5
Sр =
Слайд 68
АС = 36 см.
S∆ = · 36 · 12
В
II уровень
I вариант
№1.
Ответ: S∆= 216 см2.
№2.
S = a · ha
60 = a · 5
а = 12 (см).
S = b · hb
60 = b · 10
b = 6 (см).
Ответ: а = 12 см, b = 6 см.
№3.
1,6х = 80
х = 50
АD = 50 см
ВС = 30 см.
Ответ: 30 см, 50 см.
· 8 = 320
Слайд 69
№3.
ВН = 6 см
КМ = 6 см
НК = 8 см
ВС
Sтр = · 6 = 28 · 3 = 84 (см2).
II вариант
№1.
АН = 4 см.
S∆ = · 16 · 4 = 32 (см2).
Ответ: S∆= 32 см2.
№2.
S = a · ha
S = 4 · 14 = 56 (cм2)
S = b · hb
56 = b · 8
b = 7 (см).
Ответ: S = 56 cм2, b = 7 см.
Ответ: 84 см2.
Слайд 70Урок 9. Теорема Пифагора
Цель урока:
Рассмотреть теорему Пифагора и показать её
Слайд 73Историческая справка
VI век до н.э. – математик и философ
Слайд 75Доказательство:
а). Достроим квадрат CKPD
SCKPD = (а + b)2 = а2 +
б). ∆ВСА = ∆АКЕ = ∆ЕРМ = ∆МDВ по двум катетам.
SВСА = SАКЕ = SЕРМ = SМDВ = ab/2
в). ВАЕМ – квадрат
SВАЕМ = с2
г). SСКРD = SВАЕМ + SВСА + SАКЕ + SЕРМ + SМDВ =
= с2 + 4 · аb/2 = с2 + 2аb = а2 + 2аb + b2
Откуда, с2 = а2 + b2
Слайд 77Урок 10. Теорема, обратная теореме Пифагора
Цели урока:
Рассмотреть теорему, обратную теореме
Закрепить теорему Пифагора и совершенствовать навыки решения задач на её применение.
Слайд 81Урок 11. Решение задач по теме «теорема Пифагора»
Цели урока:
Закрепить теорему
Совершенствовать навыки решения задач на применение теоремы Пифагора и теоремы, обратной теореме Пифагора.
Слайд 84На «3»
I вариант
1. Стороны прямоугольника равны 8 см и 12 см.
2. ∆АВС,
Самостоятельная работа
= 900,
= 300, АВ = 6 см.
Найти стороны треугольника.
Слайд 85На «4»
II вариант
1. В прямоугольной трапеции меньшие стороны равны 6 см,
2. В треугольнике две стороны равны 12 см и 8 см, угол между ними – 600. Найти площадь треугольника.
Слайд 86На «5»
III вариант
1. В ∆АВС АВ = АС. Высота ВМ =
2. АВСD - квадрат, АВ = а. Найти АО.
Слайд 88Урок 12. Решение задач
Цели урока:
Закрепить знания, умения, навыки учащихся по теме
Совершенствовать навыки решения задач.
Слайд 89Ответы и указания к задачам самостоятельной работы
I вариант.
№1.
1). АС =
2). ∆ВАD,
ВD2 = АВ2 + АD2, по теореме Пифагора.
ВD =
=
= 4
Ответ: АС = ВD = 4 см.
(см.)
№2.
АС = х см
CD = 2х см
СВ2 = АВ2 + АС2
62 + х2 = (2х)2
36 = 3х2
х2 = 12
х = 2
Ответ: 2
, 4
= 900, АВ = 8 см, АD = 12 см.
I вариант.
Слайд 90Ответ: 24 см2.
II вариант.
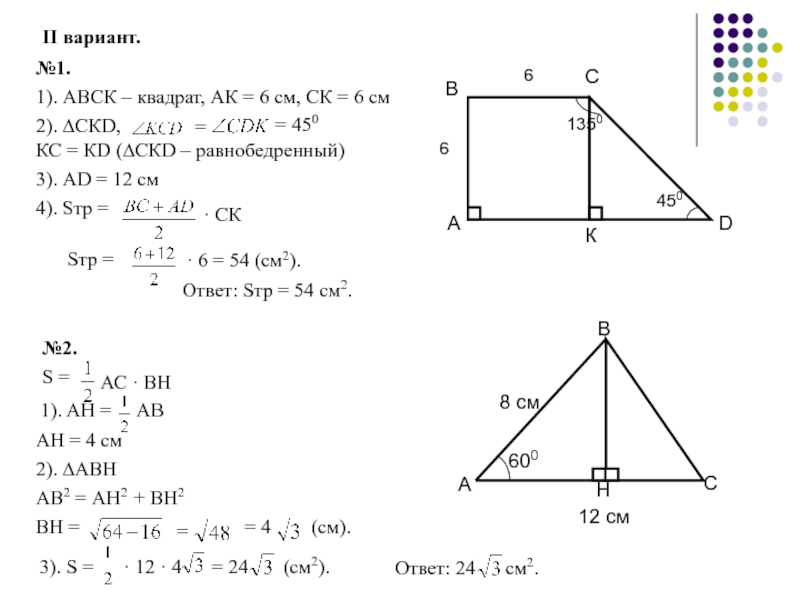
№1.
1). АВСК – квадрат, АК
2). ∆СКD,
=
КС = КD (∆СКD – равнобедренный)
3). АD = 12 см
4). Sтр =
· СК
· 6 = 54 (см2).
Ответ: Sтр = 54 см2.
№2.
S =
АС · ВН
1). АН = АВ
АН = 4 см
2). ∆АВН
АВ2 = АН2 + ВН2
ВН = = 4 (см).
=
3). S = · 12 · 4 = 24 (см2).
· 12 · 4
= 24
(см2)
Ответ: S = 24
см2
= 450
Sтр =
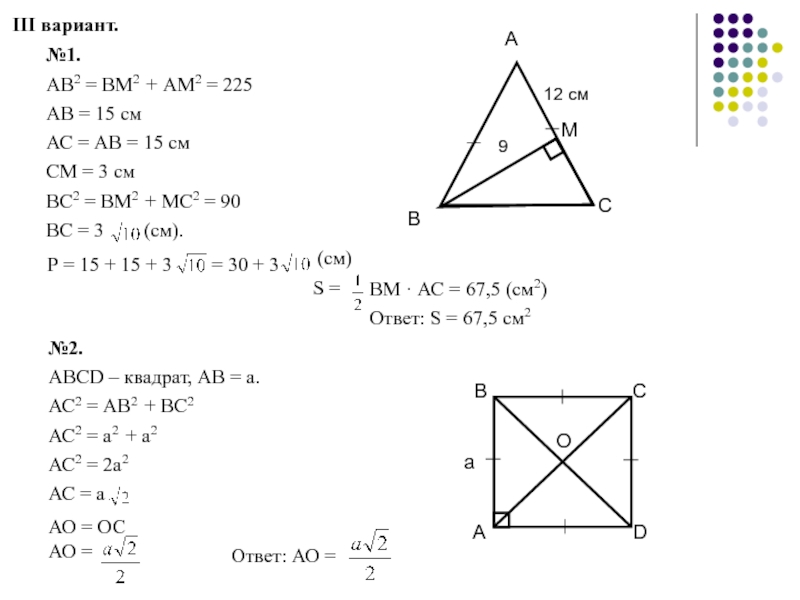
Слайд 91III вариант.
№1.
АВ2 = ВМ2 + АМ2 = 225
АВ = 15
АС = АВ = 15 см
СМ = 3 см
ВС2 = ВМ2 + МС2 = 90
ВС = 3 (см).
Р = 15 + 15 + 3
= 30 + 3
(см)
S =
ВМ · АС = 67,5 (см2)
Ответ: S = 67,5 см2
№2.
АВСD – квадрат, АВ = а.
АС2 = АВ2 + ВС2
АС2 = а2 + а2
АС2 = 2а2
АС = а
АО = ОС
АО =
Ответ: АО =
Слайд 92Домашнее задание
№ 495 (в), № 490. На «4», «5» - №
Слайд 93Урок 13. Решение задач
Цели урока:
Совершенствовать навыки решения задач по теме «Площадь».
Ознакомить
Подготовить учащихся к контрольной работе.
Слайд 97Контрольная работа
I уровень
I вариант
№1. Сторона треугольника равна 6 см, а высота
№2. Катеты прямоугольного треугольника равны 6 см. и 8 см. Найти гипотенузу и площадь треугольника.
№3. Найти площадь и периметр ромба, если его диагонали равны 8 см. и 10 см.
Слайд 98II уровень
II вариант
№1. Смежные стороны параллелограмма равны
52 см. и 30
№2. Вычислить площадь трапеции ABCD с основаниями AD и BC, если AD = 24 см, BC = 16 см, = 450, = 900.
№3. Дано ∆МКР на стороне МК отмечена точка Т так, что МТ = 5 см, КТ = 10 см, МР = 12 см, КР = 9 см. Найти площадь ∆МРТ и ∆КРТ.
Слайд 99III уровень
III вариант
№1. На стороне AD параллелограмма ABCD взята
точка Е
№2. В остроугольном треугольнике АВС проведены высоты АК и СЕ, СЕ = 12см, ВЕ = 9см, АК = 10см. Найти АС.
№3. Найти площадь ∆MKD, если М середина стороны BD.
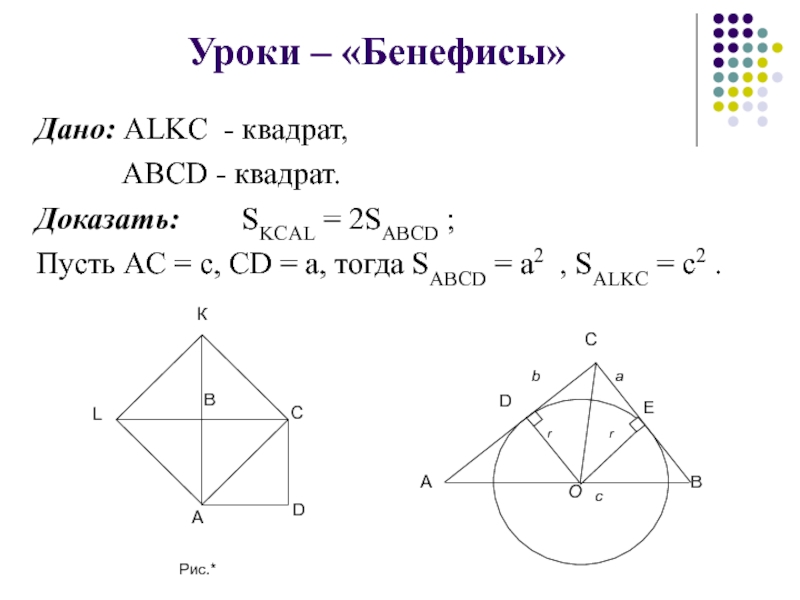
Слайд 100Дано: ALKC - квадрат,
ABCD - квадрат.
Доказать: SKCAL
Пусть AC = c, СD = a, тогда SABCD = а2 , SALKC = c2 .
Уроки – «Бенефисы»
Слайд 101I способ. (рис. *) Δ ACD – прямоугольный и, значит,
по
с2 = а2 + а2 = 2 а2, значит SALKC = 2 SABCD .
II способ. В квадрате ACKL содержится четыре треугольника АВС, а квадрате ABCD их два. Отсюда – требуемый вывод.
III способ. SΔ AKC – половина площади квадрата ACKL, но SAKC = SABCD , так как каждый состоит из двух треугольников, равных треугольнику ABC.
IV способ. Рассмотрим прямоугольный треугольник ACD. На его гипотенузе АС построен квадрат ACKL, на катете CD – квадрат ABCD, на катете AD – квадрат ABCD. Остается только применить теорему Пифагора, и требуемое равенство будет доказано.
Слайд 102Зачёт №1 по теме «Теорема Пифагора»
Билеты для устного опроса
1. 1). Теорема
2). Площадь прямоугольного треугольника равна 6, катет его равен 2. Найти другой катет и гипотенузу.
2. 1). Признак равенства прямоугольных треугольников по гипотенузе и катету.
2). Вычислить площадь равнобедренного треугольника с боковой стороной 3 и основанием 2.
3. 1). Катеты прямоугольного треугольника равны 0,3 и 0,4. Найти его гипотенузу и площадь.
2). Площадь прямоугольного треугольника , а гипотенуза равна 1. Найти длины его катетов.
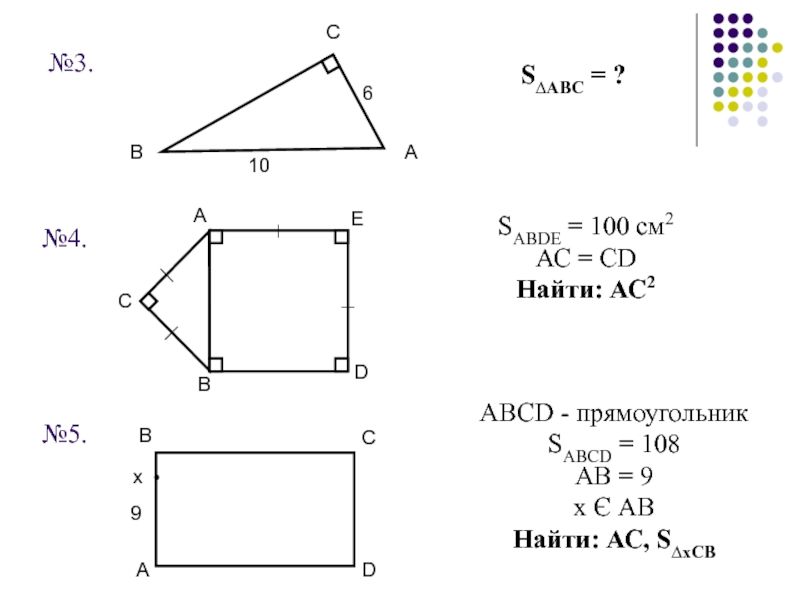
Слайд 104№3.
№4.
№5.
S∆АВС = ?
SАВDЕ = 100 см2
АС = CD
Найти: АС2
АВСD - прямоугольник
SАВСD
АВ = 9
х Є АВ
Найти: АС, S∆хСВ
Слайд 105Зачёт №2 по теме «Теорема Пифагора»
Тест 1.
Обязательная часть
1). (1) Вставьте пропущенные
В……………………………………...…треугольнике квадрат гипотенузы равен…………………………………………………………………………………
2). (1) Если в прямоугольном треугольнике АВС ( = 900), АВ2 = АС2 + СВ2, то АС2 = ……………………………………………………………………….
3). (2) Среди следующих утверждений укажите истинные и ложные:
А). В прямоугольном треугольнике любой из катетов меньше гипотенузы._____________________
Б). Из двух наклонных та больше, у которой проекция меньше._______
4). (2) Какой длины должна быть лестница?
а). 10; б). 14; в). не знаю.
5). (3) Определите неизвестный элемент.
а). 14; б). 2 ; в). 4.
6). (3) Найти АD.
а). 14; б). 28; в). не знаю.
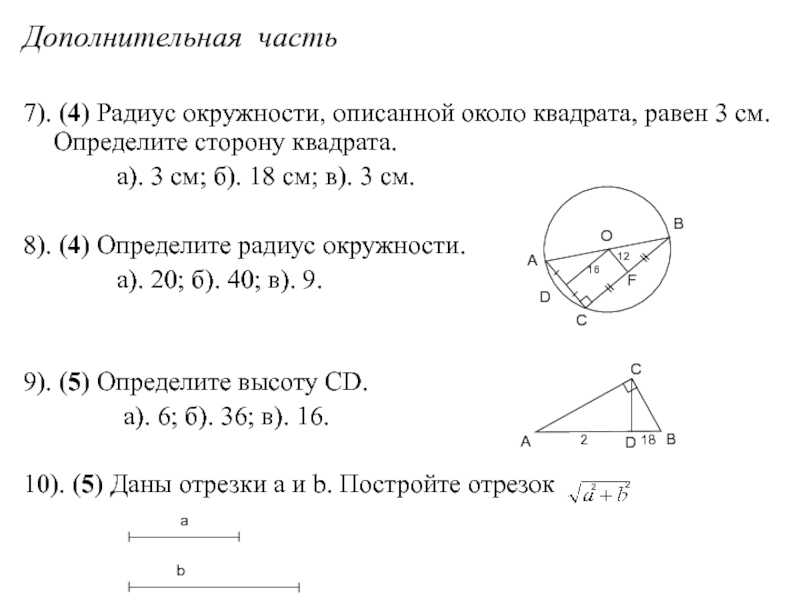
Слайд 106Дополнительная часть
7). (4) Радиус окружности, описанной около квадрата, равен 3 см.
а). 3 см; б). 18 см; в). 3 см.
8). (4) Определите радиус окружности.
а). 20; б). 40; в). 9.
9). (5) Определите высоту СD.
а). 6; б). 36; в). 16.
10). (5) Даны отрезки а и b. Постройте отрезок
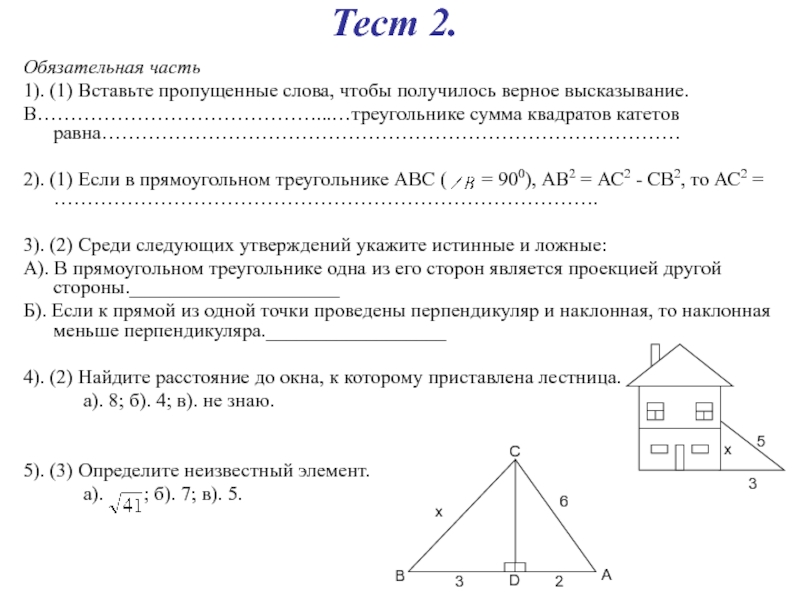
Слайд 108Тест 2.
Обязательная часть
1). (1) Вставьте пропущенные слова, чтобы получилось верное высказывание.
В……………………………………...…треугольнике
2). (1) Если в прямоугольном треугольнике АВС ( = 900), АВ2 = АС2 - СВ2, то АС2 = ……………………………………………………………………….
3). (2) Среди следующих утверждений укажите истинные и ложные:
А). В прямоугольном треугольнике одна из его сторон является проекцией другой стороны._____________________
Б). Если к прямой из одной точки проведены перпендикуляр и наклонная, то наклонная меньше перпендикуляра.__________________
4). (2) Найдите расстояние до окна, к которому приставлена лестница.
а). 8; б). 4; в). не знаю.
5). (3) Определите неизвестный элемент.
а). ; б). 7; в). 5.
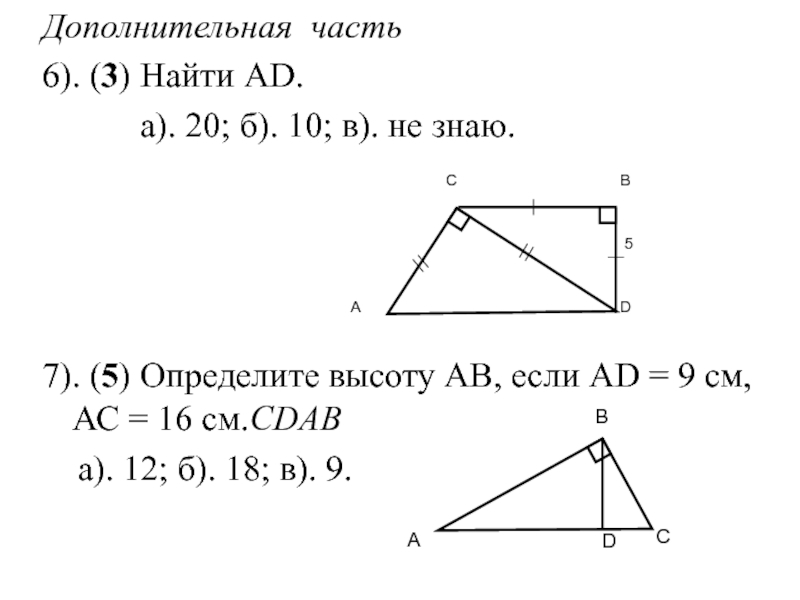
Слайд 109Дополнительная часть
6). (3) Найти АD.
а).
7). (5) Определите высоту АВ, если АD = 9 см, АС = 16 см.CDАB
а). 12; б). 18; в). 9.
Слайд 112Список литературы
1. Изучение геометрии в 7 – 9 классах: Методические рекомендации
2. Геометрия : Учебник для 7 – 9 кл. ср. шк. / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М. Просвещение, 2009.
3. Поурочные разработки по геометрии 8 класс. Дифференцированный подход. / Гаврилова Н.Ф. 2009.