- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Методическая разработка раздела образовательной и учебной программы по теме Треугольники
Содержание
- 1. Методическая разработка раздела образовательной и учебной программы по теме Треугольники
- 2. Соснина Марина СтаниславовнаУчитель математики первой квалификационной категорииПедагогический стаж 24 года В данной школе работаю 18 лет
- 3. Пояснительная записка Программа курса по геометрии
- 4. Актуальность темы «Треугольники» заключается в
- 5. Цели и задачи раздела1 Образовательные:Ввести понятие
- 6. Ожидаемые результаты при изучении главы: «Треугольники»По окончании
- 7. ПедагогическиетехнологииИКТЛекция дискуссия,консультацияПары и группысменного составаТихий опрос у доскиКонсультанты на урокеТест с закрытым ответом ИграВзаимоконтроль
- 8. Способы организации обученияФронтальнаяработаИндивидуальнаяработаГрупповаяработас единым заданием;с дифференцируемымзаданием;фронтально-вариантнаяпрограммированноеобучение;индивидуализациядля отдельных учениковс единым заданием;с дифференцируемымзаданием;
- 9. Высокий Средний
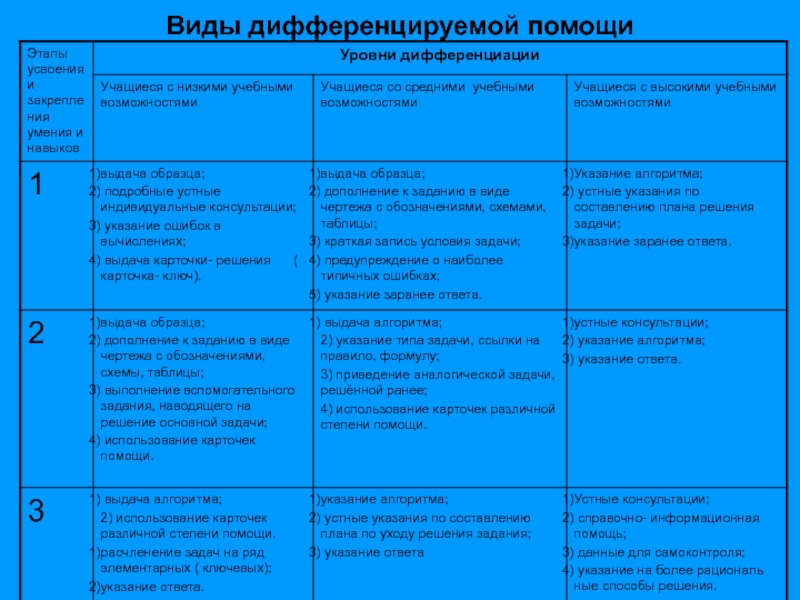
- 10. Виды дифференцируемой помощи
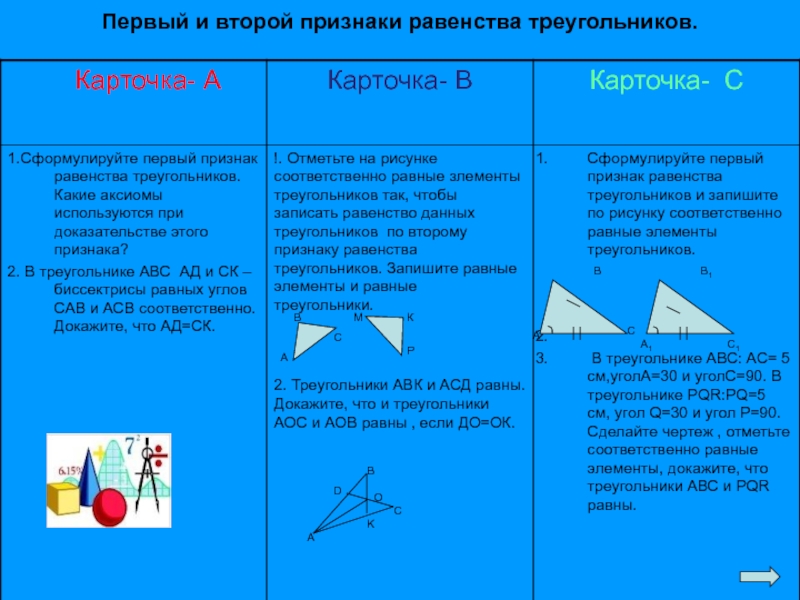
- 11. Первый и второй признаки равенства треугольников.АВСА1В1С1АВСМКРKDАBOС
- 12. Равнобедренный треугольникACBD
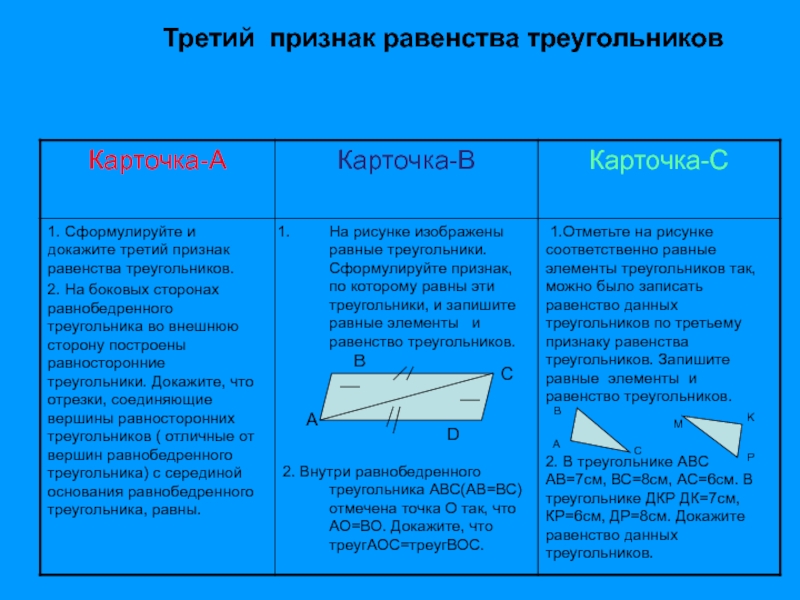
- 13. Третий признак равенства треугольниковADCBABCMKP
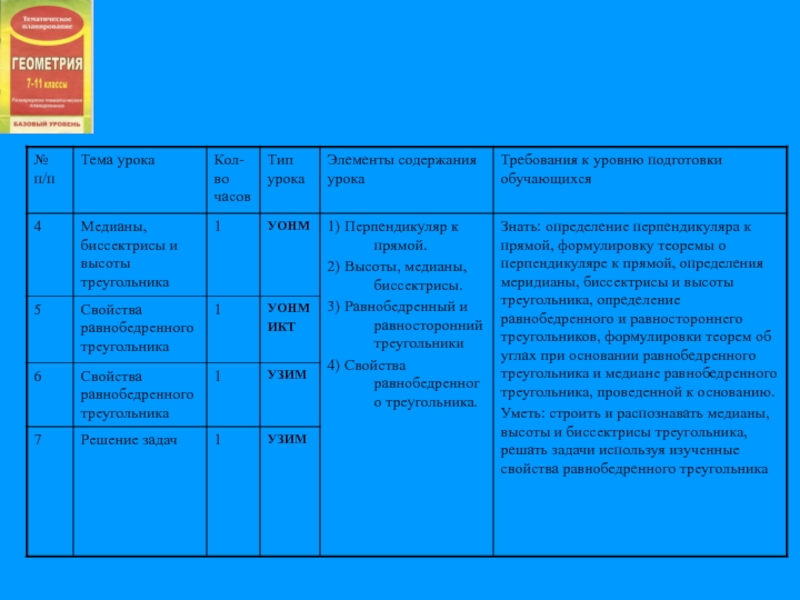
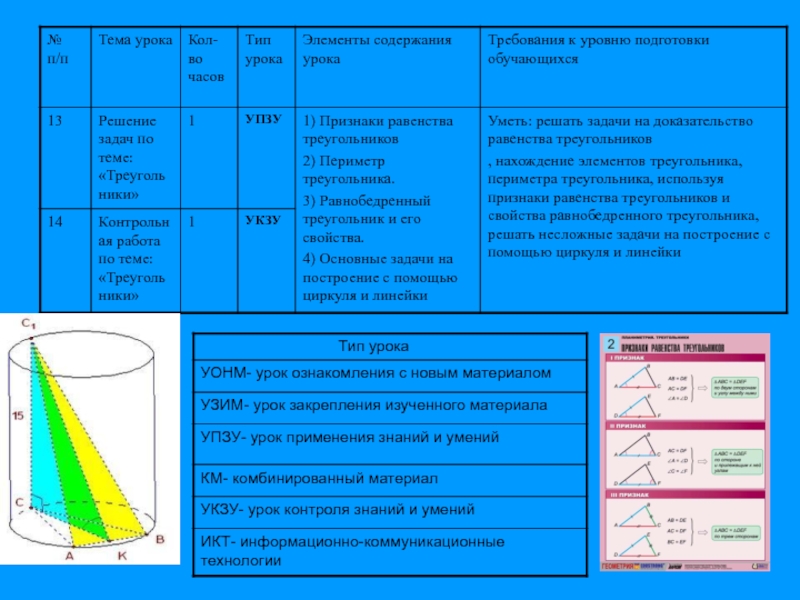
- 14. Примерное поурочное планирование. Глава 2 «Треугольники» (14 часов)
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Треугольник и его элементы.Геометрическая фигура, которая состоит
- 19. Треугольником также называется часть плоскости ограниченная отрезками
- 20. Слайд 20
- 21. Медианы, биссектрисы и высоты треугольникаaAИз точки, не
- 22. Медианы, биссектрисы и высоты треугольникаAMОтрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольникаACM2BM1M3
- 23. Медианы, биссектрисы и высоты треугольникаAA1BCОтрезок биссектрисы угла
- 24. Свойства равнобедренного треугольника.
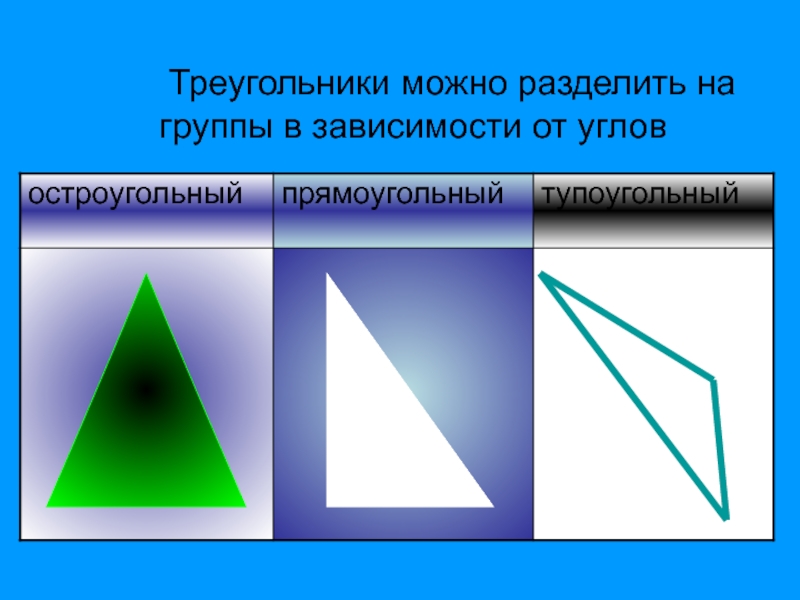
- 25. Треугольники можно разделить на группы в зависимости от углов
- 26. Первый признак равенства треугольникаЕсли две стороны и
- 27. Второй признак равенства треугольниковЕсли сторона и два
- 28. Третий признак равенства треугольниковЕсли три стороны одного
- 29. Использование компьютерных технологий
- 30. ВЕРНО. Треугольник равнобедренный. ВО – биссектриса, проведенная
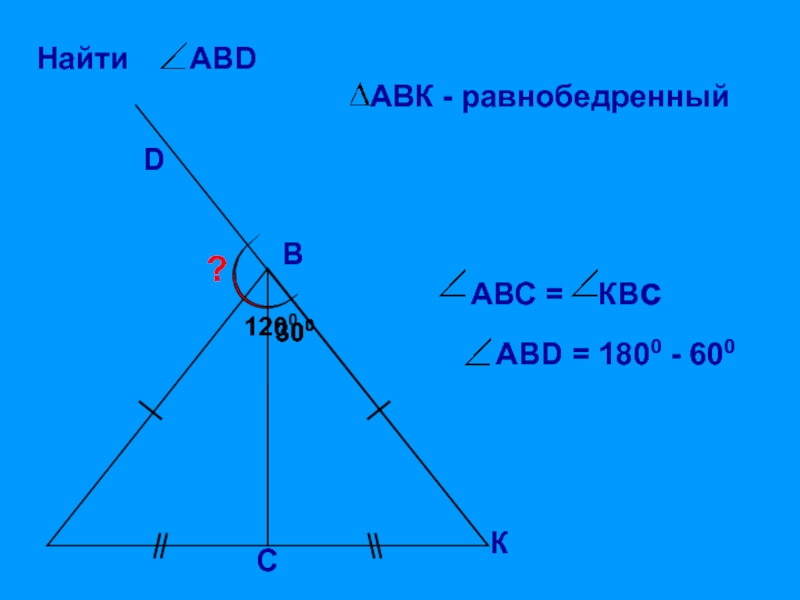
- 31. ВD?300300КС1200
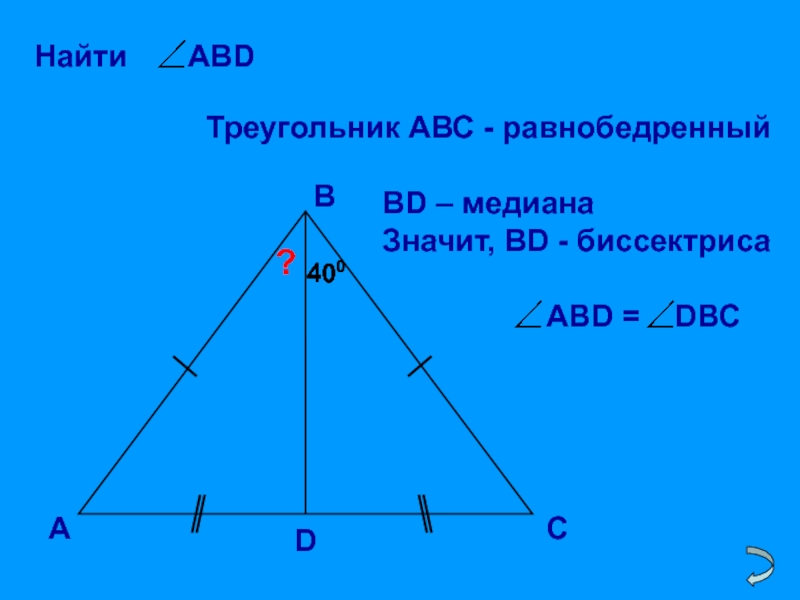
- 32. АВСD?400400Треугольник АВС - равнобедренныйВD – медианаЗначит, ВD - биссектриса
- 33. «Первый и второй признаки равенства треугольников».ОБОРУДОВАНИЕ.Учебный класс.Компьютер.
- 34. ОРГАНИЗАЦИЯ НАЧАЛА УРОКА.Орг. момент.Сообщение темы урока и
- 35. Тест на заполнение пропусков в истинном утверждении
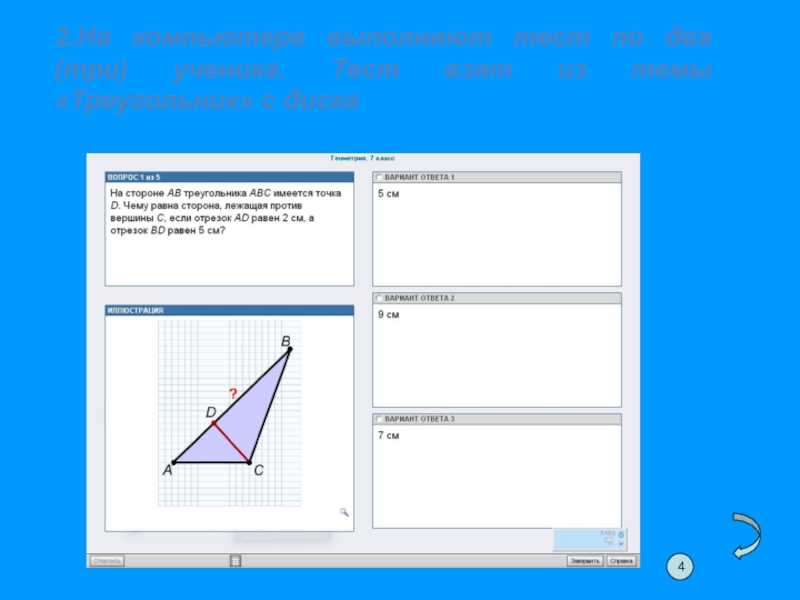
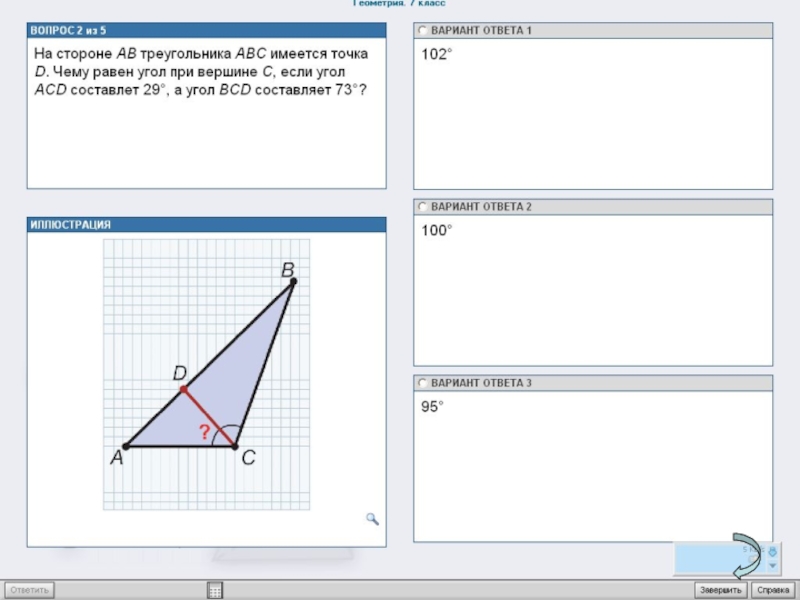
- 36. 2.На компьютере выполняют тест по два (три) ученика. Тест взят из темы «Треугольник» с диска4
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. 5
- 42. ФРОНТАЛЬНАЯ РАБОТА С КЛАССОМ НА АКТУАЛИЗАЦИЮ ОПОРНЫХ
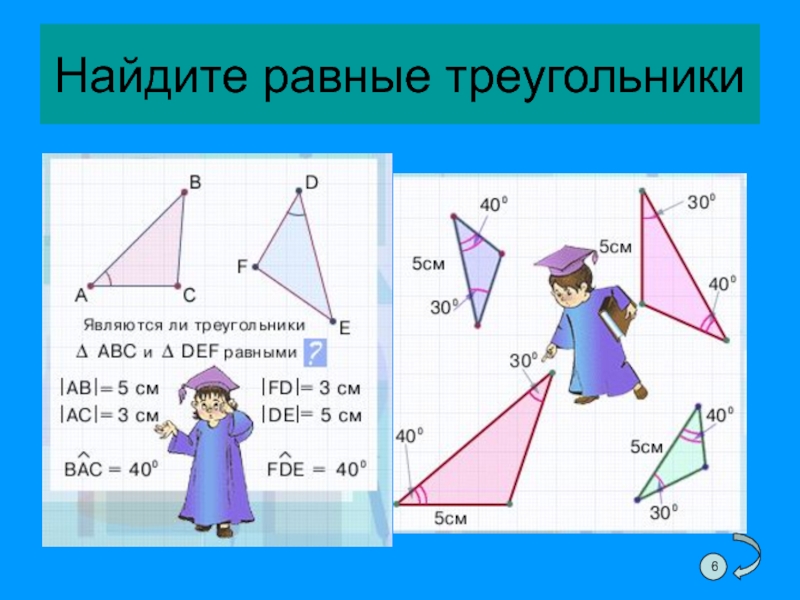
- 43. Найдите равные треугольники6
- 44. ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА В ГРУППАХ. Класс объединяется в
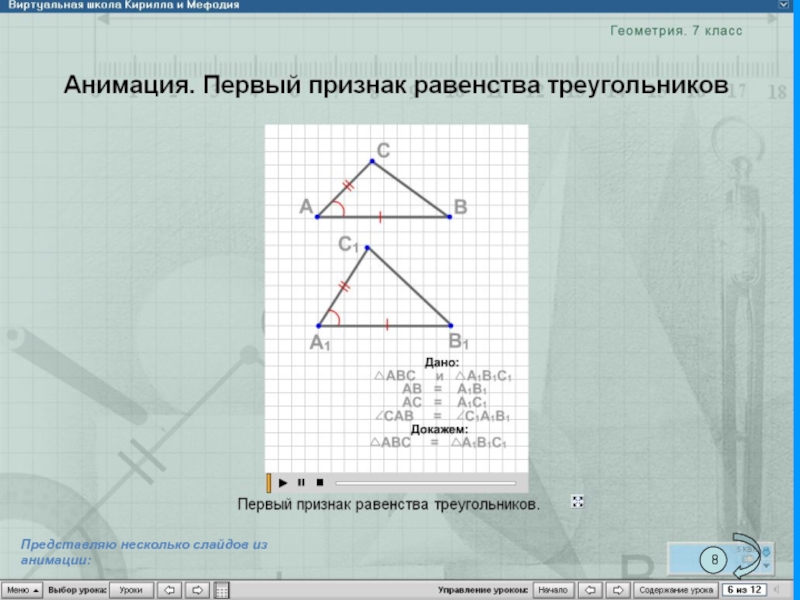
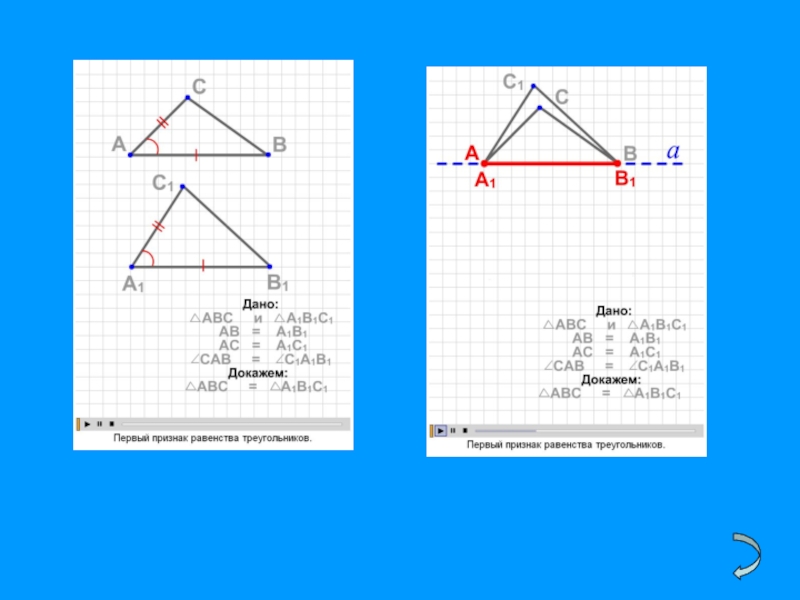
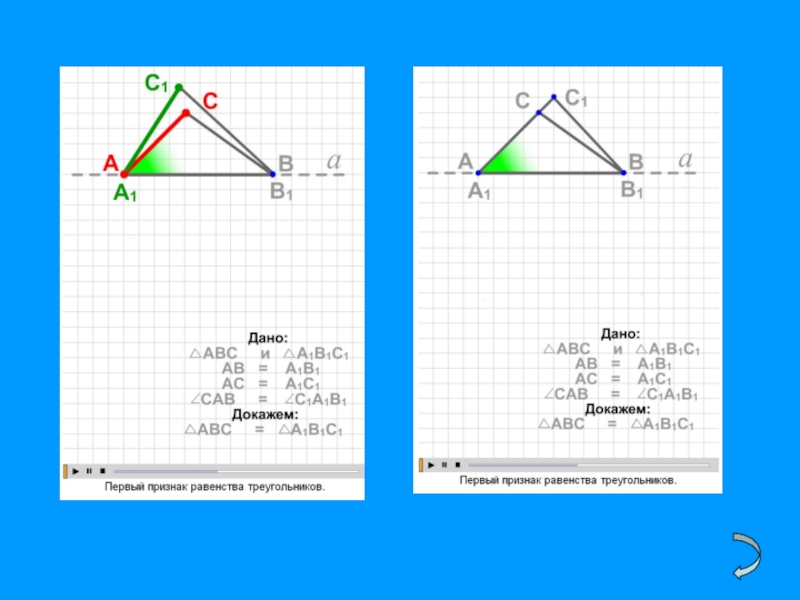
- 45. Представляю несколько слайдов из анимации:8
- 46. Слайд 46
- 47. Слайд 47
- 48. Физминутка Гимнастика для глаз Голова неподвижна. Движутся
- 49. 2. Второй признак равенства треугольников.Учащиеся записывают в
- 50. ПЕРВИЧНАЯ ПРОВЕРКА ПОНИМАНИЯ УЧАЩИМИСЯ НОВОГО МАТЕРИАЛА. Для
- 51. Терминологический диктант 1 вариант 1 Тр…угольник
- 52. ПОДВЕДЕНИЕ ИТОГОВ, ДОМАШНЕЕ ЗАДАНИЕ. Обязательный уровень:
- 53. Литература 1. Бурмистрова, Т.А. Программы общеобразовательных учреждений. Геометрия,
- 54. Геометрия удачУ каждого из нас своя ПРЯМАЯ,Им
Слайд 2Соснина Марина Станиславовна
Учитель математики первой квалификационной категории
Педагогический стаж 24 года
В
Слайд 3Пояснительная записка
Программа курса по геометрии для 7 класса разработана
Реализация данной программы рассчитана на 50 часов ( 2 часа в неделю во 2, 3 и 4 четвертях).На изучение темы « Треугольники» отводится 14 часов, контрольная работа-1час.
Осуществление представленной рабочей программы предполагает использование следующего УМК:
1. Атанасян, Л.С. Геометрия: учебник для 7-9 кл. общеобразовательных учреждений ( Текст) / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадемцев и др.- М.: Просвещение,2008.
2. Атанасян, Л.С. Геометрия: рабочая тетрадь для 7 кл. общеобразовательных учреждений ( Текст) / Л.С.Атанасян, В.Ф.Бутузов, Ю.А.Глазков,И.И.Юдина.- М.: Просвещение,2005.
3. Атанасян, Л.С. Изучение геометрии в 7-9 классах: методические рекомендации для учителя ( Текст) / Л.С.Атанасян, В.Ф.Бутузов, Ю.А.Глазков,И.И.Юдина.- М.: Просвещение,2005.
4. Зив,Б.Г. Дидактические материалы по геометрии для 7 кл (Текст)/ Б.Г.Зив, В.М.Мейлер.-М.: Просвещение,2005.
5. Саврасова,С.М. Упражнения по планиметрии на готовых чертежах ( Текст)/ С.М.Саврасова, Г.А.Ястребинецкий. – М.: Просвещение, 2004.
Методическая разработка раздела образовательной и учебной программы по теме:
«Треугольники»
Слайд 4
Актуальность темы «Треугольники» заключается в следующем:
- изучение материала существенно
Природа говорит языком математики: буквы этого языка – круги, треугольники и иные математические фигуры.
Галилей
Слайд 5Цели и задачи раздела
1 Образовательные:
Ввести понятие теоремы;
Выработать умение доказывать
Ввести новый класс задач – на построение с помощью циркуля и линейки;
Научить решать задачи на применение признаков равенства треугольников;
Научить учащихся самостоятельно выполнять рисунки по условию задачи;
Позволяет накапливать опыт доказательных рассуждений.
2. Воспитательные:
Воспитывать умение работать с имеющиеся информацией, математической культуры и речи;
Умение слушать товарищей;
Воспитывать отношение к геометрии , как к части общечеловеческой культуры через знакомство с историей развития геометрии, эволюцией математических идей.
3. Развивающие:
Получить представление о треугольниках, как математическом аппарате решения разнообразных задач из математики, смежных областей знаний;
Овладеть математическими знаниями и умениями, необходимыми в повседневной жизни для изучения школьных естественно- научных дисциплинах на базовом уровне;
Проводить доказательные рассуждения в ходе решения задач;
Развить логическое мышление, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе по соответствующей специальности.
Слайд 6Ожидаемые результаты при изучении главы: «Треугольники»
По окончании изучения темы
ученик знает:
что такое
формулировку теоремы о перпендикуляре к прямой, знать и уметь доказывать теоремы о свойствах равнобедренного треугольника;
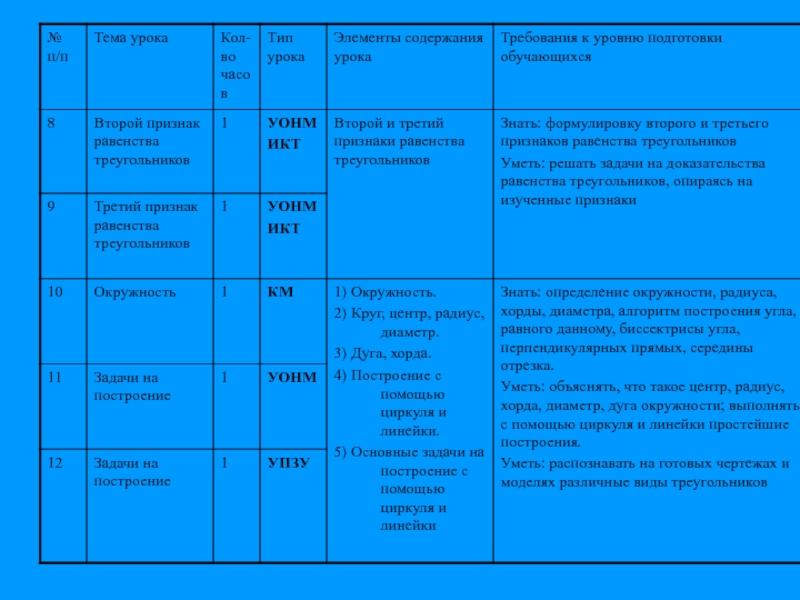
формулировки и доказательства второго и третьего признаков равенства треугольников;
определение окружности;
навыки решения задач на построение с помощью циркуля и линейки.
ученик умеет:
- объяснить, какая фигура называется треугольником, и назвать его элементы;
объяснить, какой отрезок называется перпендикуляром, проведенным из данной точки к данной прямой, какие отрезки называются медианой, биссектрисой, высотой треугольника, какой треугольник называется равнобедренным, равносторонним;
объяснить, что такое центр, радиус, хорда, диаметр, дуга окружности ,выполнять с помощью циркуля и линейки простейшие построения: отрезка, равного данному; угла, равного данному; биссектрисы данного угла; прямой, походящей через данную точку и перпендикулярной к данной прямой; середины данного отрезка; применять простейшие построения при решение задач;
решать задачи на построение с помощью циркуля и линейки.
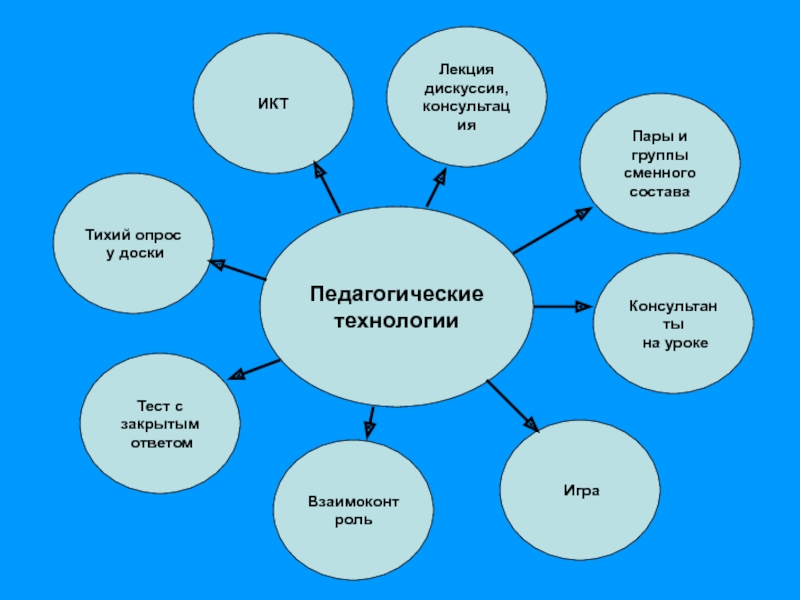
Слайд 7Педагогические
технологии
ИКТ
Лекция дискуссия,
консультация
Пары и группы
сменного состава
Тихий опрос
у доски
Консультанты
на уроке
Тест с
ответом
Игра
Взаимоконтроль
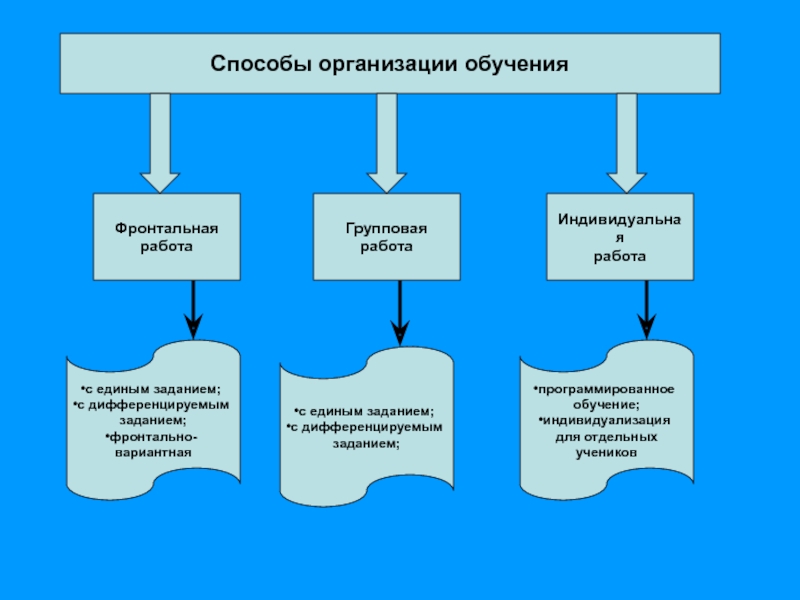
Слайд 8Способы организации обучения
Фронтальная
работа
Индивидуальная
работа
Групповая
работа
с единым заданием;
с дифференцируемым
заданием;
фронтально-вариантная
программированное
обучение;
индивидуализация
для отдельных учеников
с единым заданием;
с дифференцируемым
заданием;
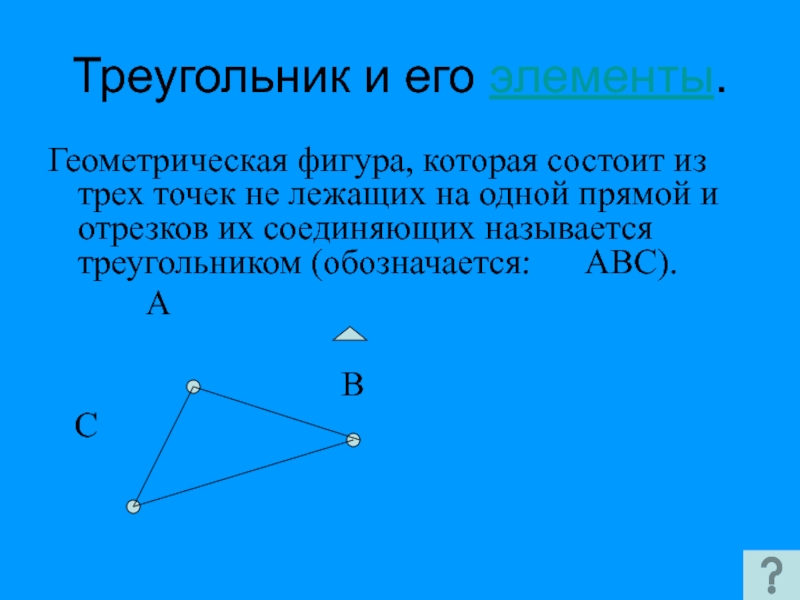
Слайд 18Треугольник и его элементы.
Геометрическая фигура, которая состоит из трех точек не
А
В
С
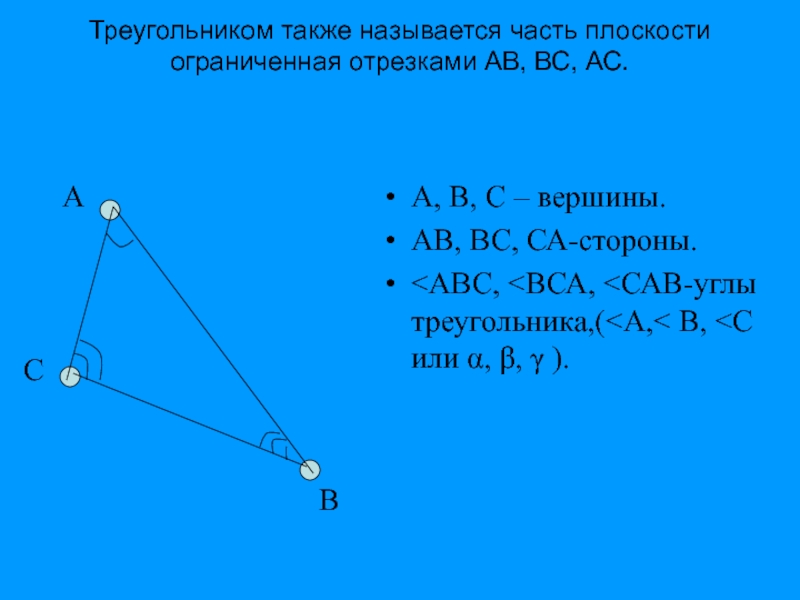
Слайд 19Треугольником также называется часть плоскости ограниченная отрезками АВ, ВС, АС.
С
В
А, В, С – вершины.
АВ, ВС, СА-стороны.
<АВС, <ВСА, <САВ-углы треугольника,(<А,< В, <С или α, β, γ ).
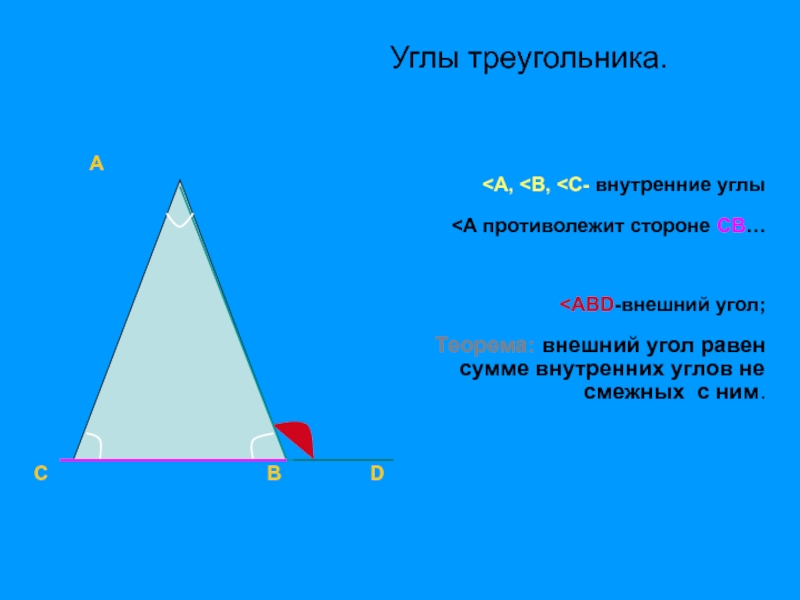
Слайд 20
А
<А, <В, <С- внутренние углы
<А противолежит стороне СВ…
<АВD-внешний угол;
Теорема: внешний угол равен
сумме внутренних углов не
смежных с ним.
С В D
Слайд 21Медианы, биссектрисы и высоты треугольника
a
A
Из точки, не лежащей на прямой, можно
a
H
A
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник
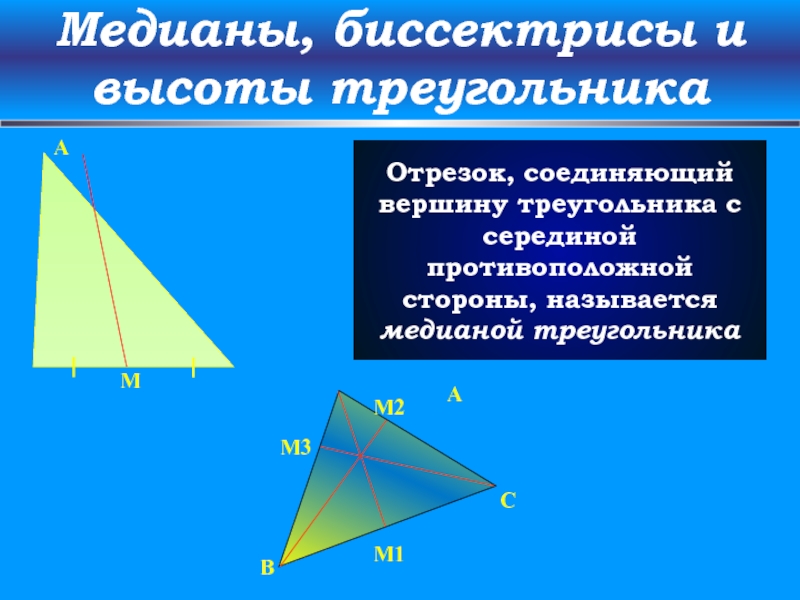
Слайд 22Медианы, биссектрисы и высоты треугольника
A
M
Отрезок, соединяющий вершину треугольника с серединой противоположной
A
C
M2
B
M1
M3
Слайд 23Медианы, биссектрисы и высоты треугольника
A
A1
B
C
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника
A
B
H
C
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника
Слайд 24Свойства равнобедренного треугольника.
А
ВС- основание.
Теорема. В равнобедренном
треугольнике углы
при основании равны.
В С
Теорема. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
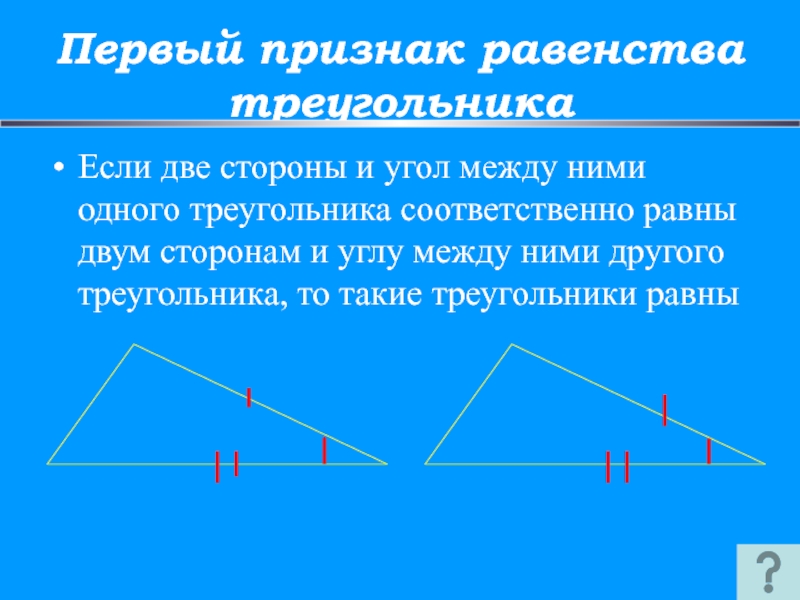
Слайд 26Первый признак равенства треугольника
Если две стороны и угол между ними одного
Слайд 27Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла
Слайд 28Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трем
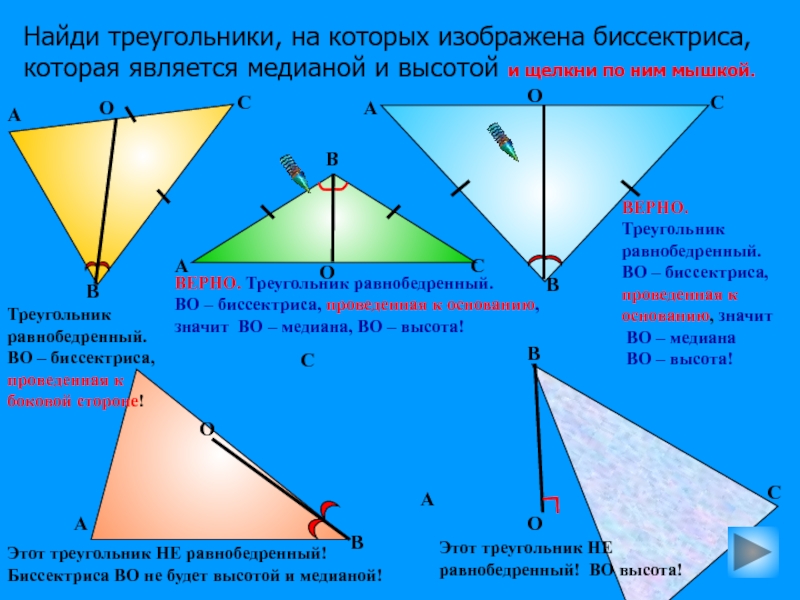
Слайд 30ВЕРНО. Треугольник равнобедренный.
ВО – биссектриса, проведенная к основанию, значит ВО
Найди треугольники, на которых изображена биссектриса,
которая является медианой и высотой и щелкни по ним мышкой.
Этот треугольник НЕ равнобедренный!
Биссектриса ВО не будет высотой и медианой!
В
А
С
О
В
В
В
В
С
С
С
С
А
А
А
А
Этот треугольник НЕ
равнобедренный! ВО высота!
О
О
О
О
ВЕРНО.
Треугольник
равнобедренный.
ВО – биссектриса, проведенная к основанию, значит
ВО – медиана
ВО – высота!
Треугольник
равнобедренный.
ВО – биссектриса, проведенная к боковой стороне!
Слайд 33«Первый и второй признаки равенства треугольников».
ОБОРУДОВАНИЕ.
Учебный класс.
Компьютер.
Мультимедийный проектор.
Диск «Уроки
Транспортиры, масштабные линейки, набор кальки, магнитофон.
ЦЕЛЬ УРОКА.
Исследовать треугольники на предмет равенства с выводом результата.
Доказать первый и второй признаки равенства треугольников.
Развитие компетенций: уметь наблюдать, анализировать, обрабатывать полученную информацию, делать выводы;
уметь сотрудничать и работать в группе.
СТРУКТУРА УРОКА.
Организация начала урока.
Проверка выполнения домашнего задания.
Актуализация опорных знаний, проверка успешности усвоения материала с помощью единичных тестирований и последующими комментариями к ним.
Исследовательская работа в группах.
Усвоение новых знаний.
Первичная проверка понимания учащимися нового материала.
Подведение итогов урока, домашнее задание.
1
Слайд 34ОРГАНИЗАЦИЯ НАЧАЛА УРОКА.
Орг. момент.
Сообщение темы урока и плана работы на уроке.
Вызов
Проведение математического теста
Вызов поочерёдно двух (трех) учеников па выполнение теста на компьютере.
ПРОВЕРКА ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ.
1.У доски выполняют решение домашних номеров:
№ 89-а (из рубрики практическое задание); № 1 (был предложен под запись).
2
Слайд 35Тест на заполнение пропусков в истинном утверждении и в формулировках определений
1. Сумму трех сторон треугольника называют его … . (1 бал)
2. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется … треугольника. (1 бал)
3. Медиана равнобедренного треугольника, проведенная к основанию, является … и высотой. (2 бала)
4. Если равнобедренный треугольник перегнуть по медиане, проведённой к основанию, то в этом случае медиана является … … этого треугольника. (2 бала)
5. Ось симметрии равнобедренного треугольника пересекает основание под углом в … градусов. (2 бала)
6. Если в равнобедренном треугольнике АСВ с основанием АВ проведена биссектриса СД и угол АСД= 86 ,то угол АСВ = …. (3 бала)
7. Если в равнобедренном треугольнике МКР с основанием МР проведена медиана КД и если МД=9,9см, то МР= … . (3 бала)
8. Если две высоты треугольника совпадают с его сторонами, то треугольник … ( вид треугольника). (4 бала)
Вариант 2
по биссектриссе, проведённой,к основанию, то биссектрисса является … … этого треугол1. Отрезки, соединяющие попарно три точки, не лежащие на одной прямой, называют … треугольника. (1 бал)
2. Отрезок перпендикуляра, проведенного из вершины треугольника к прямой, содержащей противоположную сторону, называется … треугольника. (1 бал)
3. Биссектриса равнобедренного треугольника, проведённая к основанию, является высотой и … . (2 бала)
4. Если равнобедренный треугольник перегнуть ьника. (2 бала)
5.Ось симметрии равностороннего треугольника пересекает основание под углом … градусов (2 бала)
6. Если в равнобедренном треугольнике АВС с основанием АС проведена высота Вм и угол АВС= 68 ,то угол СВМ= …. (3 бала)
7. Если в равнобедренном треугольнике АВС основанием АВ проведена биссектриса СД и АВ=17,6см, то ВД= … . (3 бала)
8. Если все три высоты треугольника пересекаются в одной из его вершин, то треугольник … ( вид треугольника). (3 бала)
3
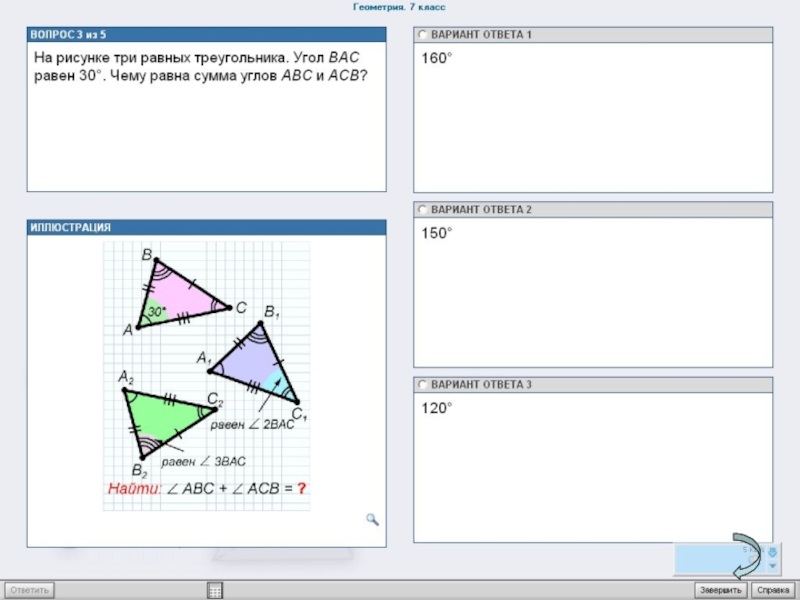
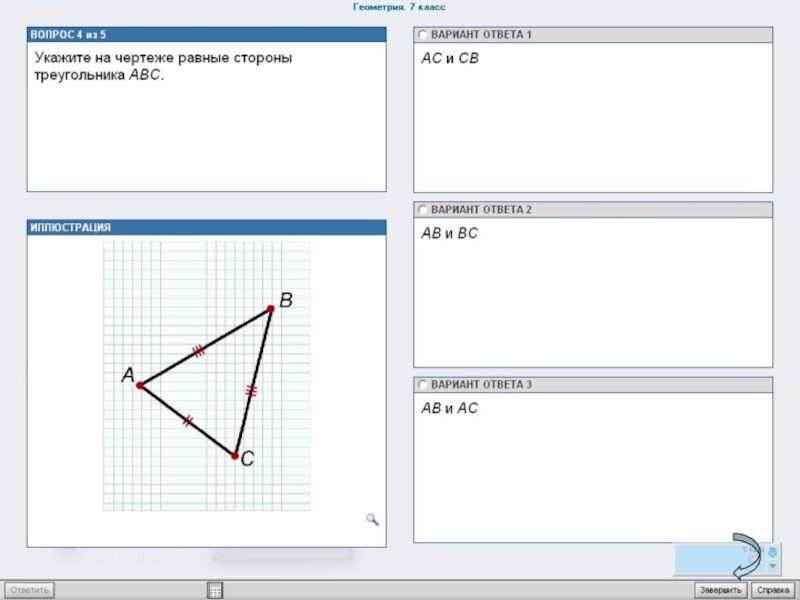
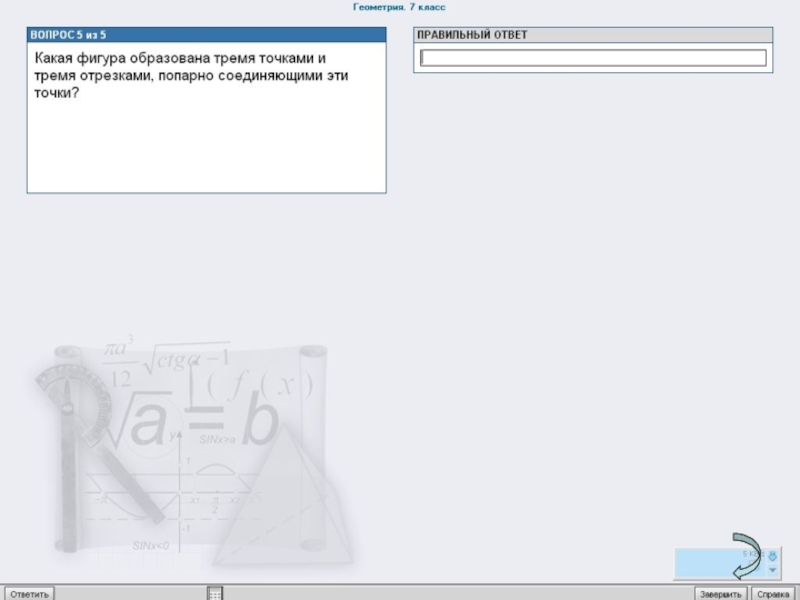
Слайд 362.На компьютере выполняют тест по два (три) ученика. Тест взят из
4
Слайд 42
ФРОНТАЛЬНАЯ РАБОТА С КЛАССОМ НА АКТУАЛИЗАЦИЮ ОПОРНЫХ ЗНАНИЙ.
После коллективной работы с классом, учащиеся открывают тетради с домашней работой и проверяют её выполнение. К этому времени вызванные к доске ученики готовы к ответу. По обстоятельствам задаются вопросы, идут комментарии.
А В
Слайд 44ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА В ГРУППАХ.
Класс объединяется в группы от 2-х до
Постройте на кальке ∆ МРО, у которого угол Р равен 90 , РО= 4 см, РМ = 3 см.
Сравните этот треугольник с треугольником АВС из № 89-в, с помощью наложения. Сделайте вывод.
Сколько равных элементов у этих треугольников? Какие это элементы?
Постройте в тетради ∆АВС, у которого АВ= 3 см, угол А = 60°, угол В = 40°, и ∆КРО на кальке, у которого КО = 3 см, угол К = 60°, угол О = 40°.
Сравните эти треугольники с помощью наложения. Сделайте вывод.
Сколько равных элементов у этих треугольников? Какие это элементы?
Как вы думаете, когда ещё можно утверждать, что треугольники, при равенстве каких либо трёх элементов, окажутся равными?
Всегда ли будут равны треугольники, если у них равны два элемента?
7
Слайд 48Физминутка Гимнастика для глаз
Голова неподвижна. Движутся только глаза. В вытянутой
Круговые движения глазами в одном, а затем в другом направлении - (6 - 7 раза)
Нарисуйте глазами треугольники: маленький, средний, большой.
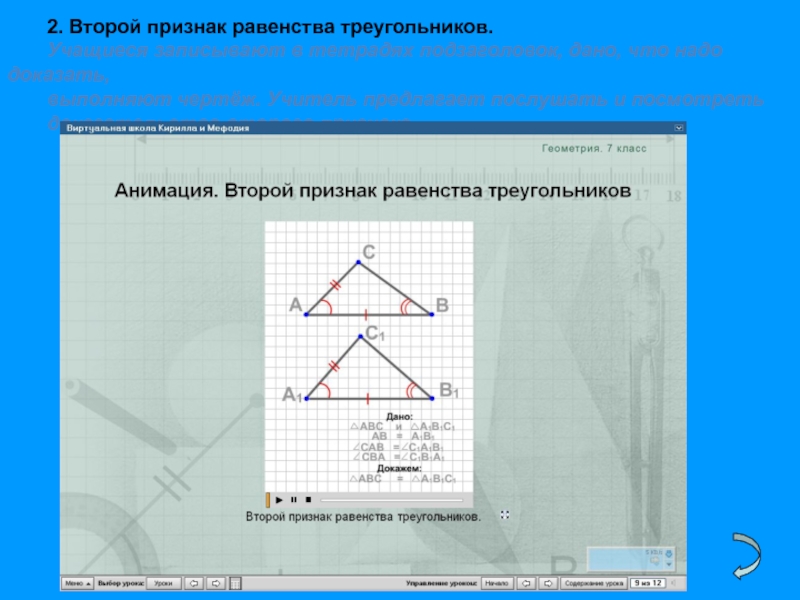
Слайд 492. Второй признак равенства треугольников.
Учащиеся записывают в тетрадях подзаголовок, дано, что
выполняют чертёж. Учитель предлагает послушать и посмотреть
доказательство второго признака.
Слайд 50ПЕРВИЧНАЯ ПРОВЕРКА ПОНИМАНИЯ УЧАЩИМИСЯ НОВОГО МАТЕРИАЛА.
Для доказательства равенства треугольников будем
Работаем по готовым чертежам, которые проецируются на экран с помощью проектора (одно из заданий оформляется в тетради) и по тренажёру с диска.
Слайд 51Терминологический диктант
1 вариант
1 Тр…угольник
3 Пр…моугольный
тр…угольник
4 Перес…чение
5 Б…ссектриса 6 Г…потенуза
7 Осн…вание 8 Док…зательство
2 вариант
1 В…ршина
2 Пр…мая
3 Ст…рона
4 Равност…ронний тр…угольник
5 Т…орема
6 М…диана
7 Выс…та
8 Ц…ркуль
Слайд 52
ПОДВЕДЕНИЕ ИТОГОВ, ДОМАШНЕЕ ЗАДАНИЕ.
Обязательный уровень: п.15, №121,формулировка теоремы.
Повышенный
Творческий уровень: Подготовить презентацию по данной теме.
Слайд 53Литература
1. Бурмистрова, Т.А. Программы общеобразовательных учреждений. Геометрия, 7-9 классы. – М.:
2. Ганеев, Х.Ж. Теоретические основы развивающего обучения математике. – Екатеринбург, 1997.
3. Гусев, В.А. Психолого-педагогические основы обучения математике. М; 2003.
4. Григорьева, Т.П., Иванова, Т.А., Кузнецова, Л.И., Перевощикова, Е.Н. Основы технологии развивающего обучения математике: Учеб. пособие/ Под ред. Т.А.Ивановой. – Н.Новгород,1997.
5. Дусавицкий, А.К. Развитие личности в учебной деятельности. – М., 1996
6. ЕГЭ. Математика, 9 класс Экспериментальная экзаменационная работа. Типовые тестовые задания / Л.Д. Лаппо, М.А. Попов. - М.: Издательство «Экзамен», 2007. - 48 с. (Серия «ЕГЭ. 9 кл. Типовые тестовые задания») - ISBN 5-472-1-0164807
7. Епишева, О.Б. Технология обучения математики на основе деятельностного подхода .- М: Просвещение. 2003
8. Иванова ,Т.А., Григорьева Т.П. Теоретические основы обучения математике в средней школе: Учеб. пособие. - Н.Новгород, 2003.
9. Колеченко, А.К. Энциклопедия педагогических технологий: Пособие для преподавателей. – СПб.: КАРО, 2004.
10. Манвелов,С.Г. Конструирование современного урока математики. .- М: Просвещение. 2008.
11. Саранцев, Г.И. Методика обучения математики в средней школе .- М: Просвещение. 2007
12. Фридман, Л.М. Психолого-педагогические основы обучения математике в школе. - М.: Просвещение, 1993.
Слайд 54Геометрия удач
У каждого из нас своя ПРЯМАЯ,
Им пересечься только раз дано.
И
Свою беду, судьбу, удачу, но…
У каждого из нас своя ОКРУЖНОСТЬ,
Непроходящий круг проблем, забот,
Потерянность, утраченность, ненужность
И первый к потепленью поворот.
У каждого из нас свой ТРЕУГОЛЬНИК.
И, убегая от страстей своих,
Мы мечемся, настигнутые болью
И счастьем, поделенным на троих.