- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Материалы для учителя: презентация большая (основные свойства простейших геометрических фигур)
Содержание
- 1. Материалы для учителя: презентация большая (основные свойства простейших геометрических фигур)
- 2. Геометрические фигурыГеометрия – это наука о свойствах
- 3. Всякую геометрическую фигуру мы представляем себе составленной из точек
- 4. В школе изучается геометрия, называемая евклидовой, по
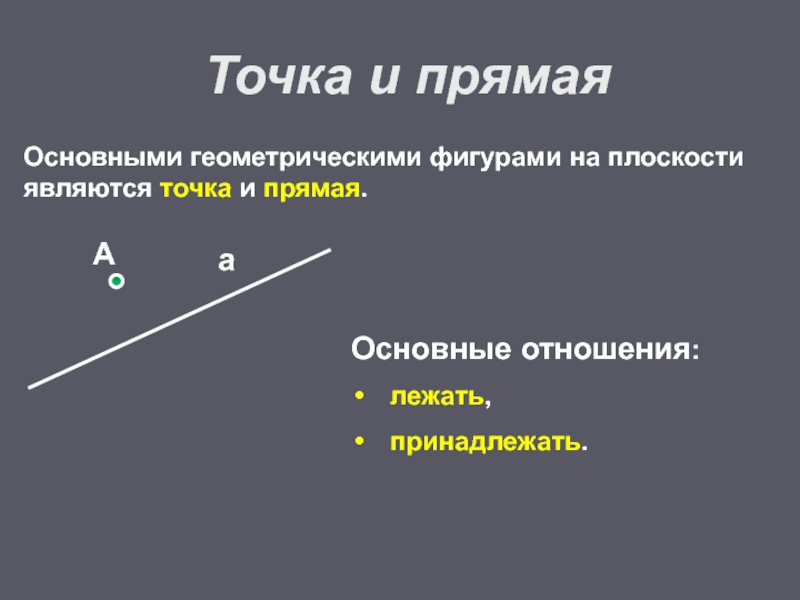
- 5. Основными геометрическими фигурами на плоскости являются точка и прямая.Точка и прямаяОсновные отношения:лежать,принадлежать.Аа
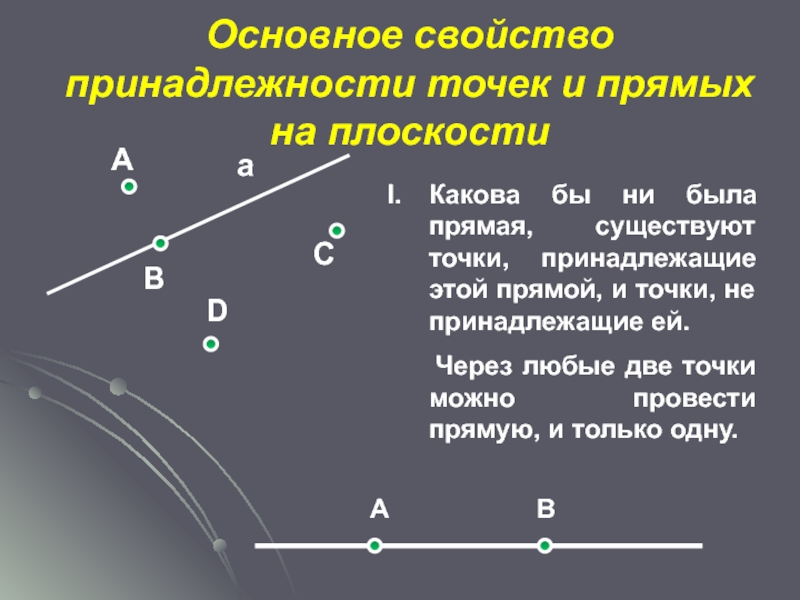
- 6. АаВСDКакова бы ни была прямая, существуют точки,
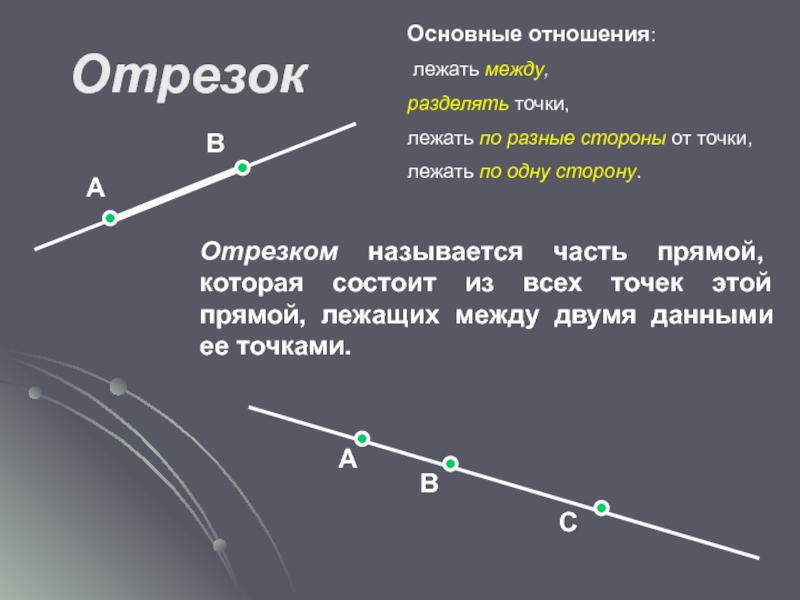
- 7. ОтрезокОсновные отношения: лежать между, разделять точки,лежать по
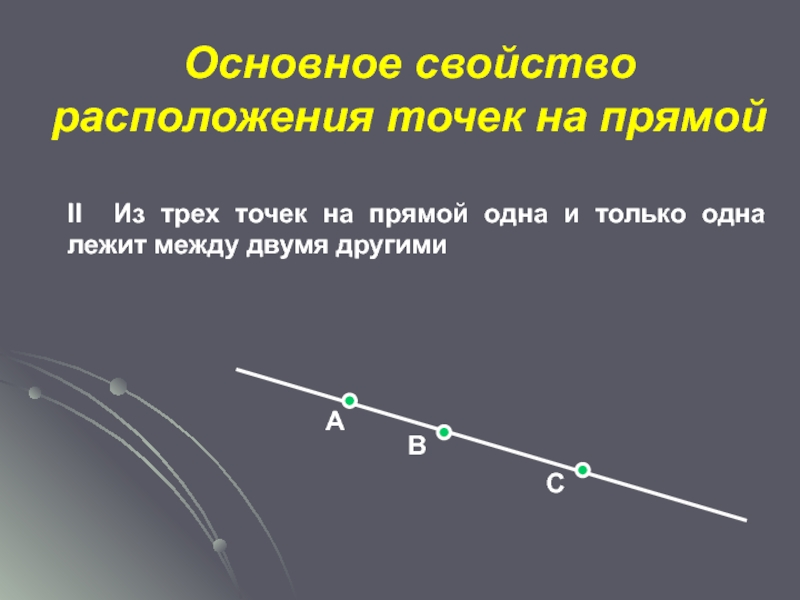
- 8. Основное свойство расположения точек на прямойАВСII Из
- 9. Основное свойство измерения отрезковДля измерения отрезков применяют
- 10. ПолуплоскостиАВСDОсновное свойство расположения точек относительно прямой на плоскости IV Прямая разбивает плоскость на две полуплоскости.
- 11. ПолупрямаяА Х
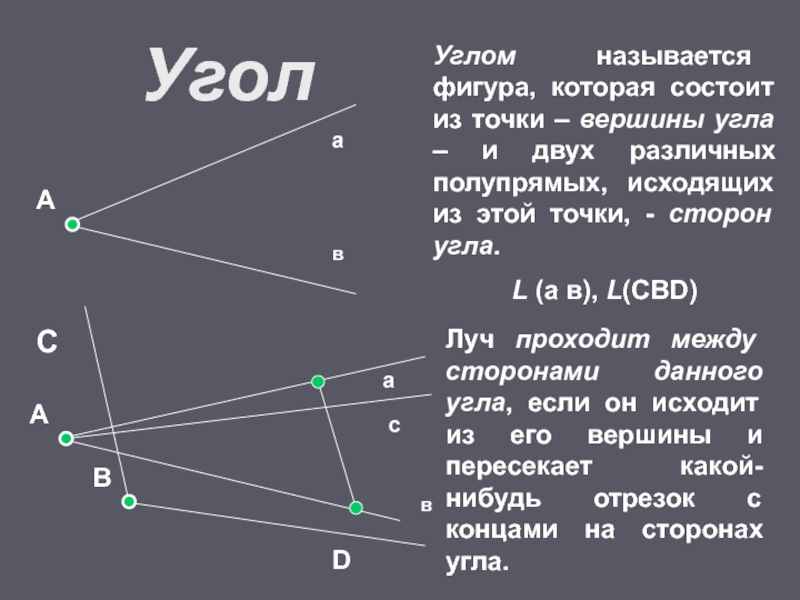
- 12. УголВАавСDУглом называется фигура, которая состоит из точки
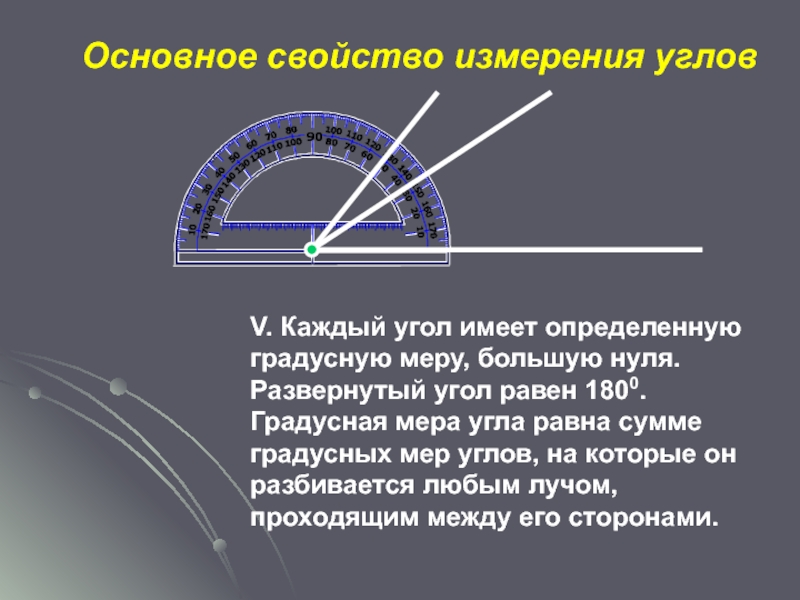
- 13. Основное свойство измерения угловV. Каждый угол имеет
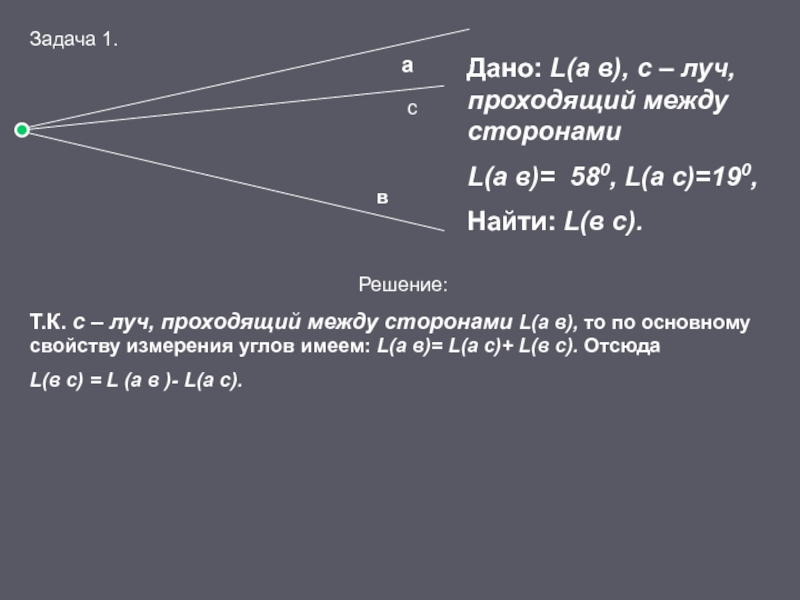
- 14. авсДано: L(а в), с – луч, проходящий
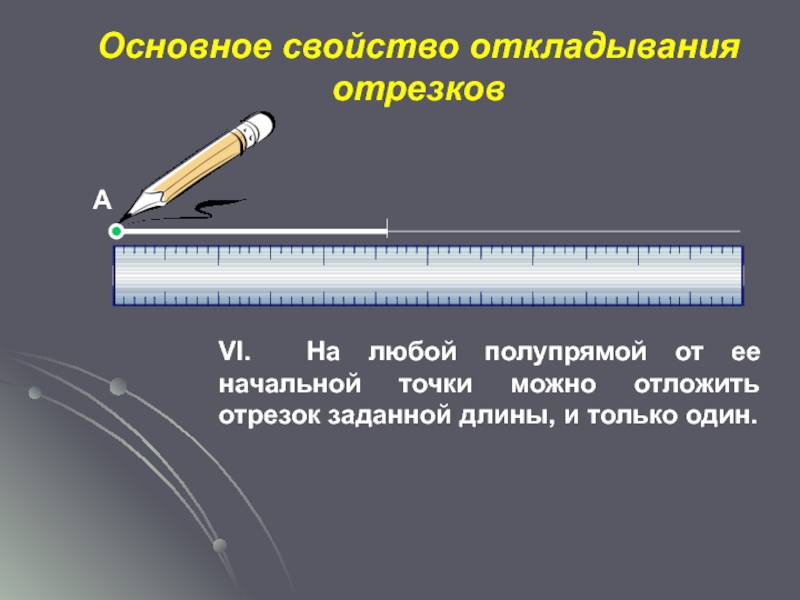
- 15. Основное свойство откладывания отрезковVI. На любой полупрямой
- 16. Основное свойство откладывания угловА
- 17. Измерение углов на местностиИзмерение углов на местности
- 18. Слайд 18
- 19. ТреугольникТреугольником называется фигура, которая состоит из трех
- 20. Слайд 20
- 21. Два отрезка называются равными, если они имеют
- 22. А
- 23. Основное свойство существования треугольника равного данномуVIII.
- 24. А
- 25. Параллельные прямыеа b
- 26. Основное свойство параллельных прямыха || bаВbIX. Через
- 27. В развитии геометрии важную роль сыграла аксиома,
- 28. Лобачевский не получил противоречивых выводов. На основании
- 29. Аксиомы. Теоремы и доказательства
- 30. ТЕОРЕМА: Если прямая, не проходящая ни через
Слайд 2Геометрические фигуры
Геометрия – это наука о свойствах геометрических фигур. Слово
Слайд 4В школе изучается геометрия, называемая евклидовой, по имени Евклида, создавшего руководство
Евклид – древнегреческий ученый (III в. до н.э.)
Слайд 5Основными геометрическими фигурами на плоскости являются точка и прямая.
Точка и прямая
Основные
лежать,
принадлежать.
А
а
Слайд 6
А
а
В
С
D
Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и
Через любые две точки можно провести прямую, и только одну.
Основное свойство принадлежности точек и прямых на плоскости
А В
Слайд 7Отрезок
Основные отношения:
лежать между,
разделять точки,
лежать по разные стороны от точки,
лежать
Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными ее точками.
А
В
А
В
С
Слайд 8Основное свойство расположения точек на прямой
А
В
С
II Из трех точек на прямой
Слайд 9Основное свойство измерения отрезков
Для измерения отрезков применяют различные измерительные инструменты
III
M N K
Слайд 10Полуплоскости
А
В
С
D
Основное свойство расположения точек относительно прямой на плоскости
IV Прямая разбивает
Слайд 11Полупрямая
А Х У
Полупрямой или лучом называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной ее точки
Различные полупрямые одной и той же прямой, имеющие общую начальную точку, называют дополнительными.
Слайд 12Угол
В
А
а
в
С
D
Углом называется фигура, которая состоит из точки – вершины угла –
L (а в), L(СВD)
А
а
в
с
Луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла.
Слайд 13Основное свойство измерения углов
V. Каждый угол имеет определенную градусную меру, большую
Слайд 14а
в
с
Дано: L(а в), с – луч, проходящий между сторонами
L(а в)= 580,
Найти: L(в с).
Решение:
Т.К. с – луч, проходящий между сторонами L(а в), то по основному свойству измерения углов имеем: L(а в)= L(а с)+ L(в с). Отсюда
L(в с) = L (а в )- L(а с).
Задача 1.
Слайд 15Основное свойство откладывания отрезков
VI. На любой полупрямой от ее начальной точки
А
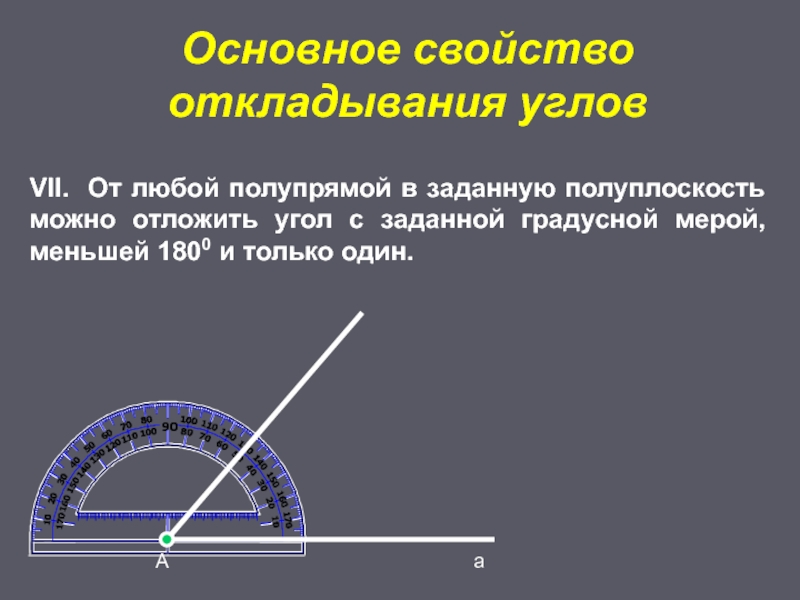
Слайд 16Основное свойство откладывания углов
А
VII. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 1800 и только один.
Слайд 17Измерение углов на местности
Измерение углов на местности проводится с помощью специальных
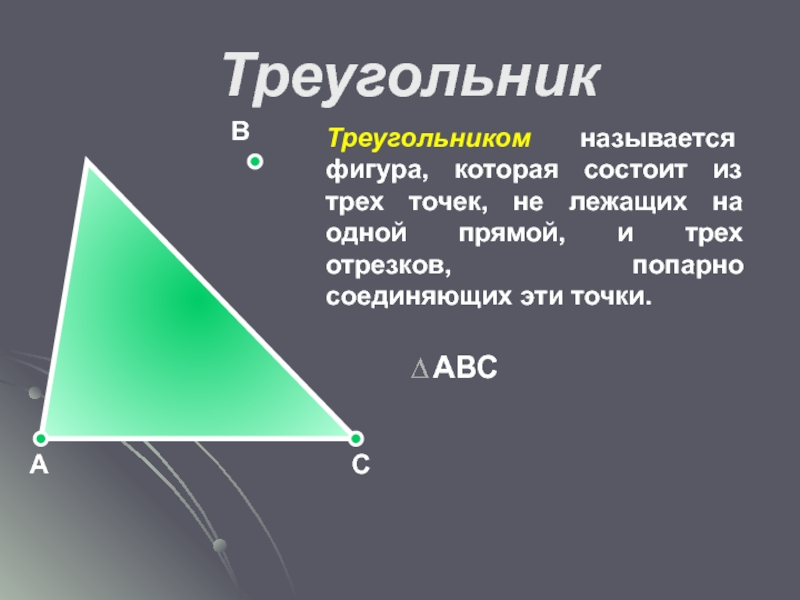
Слайд 19Треугольник
Треугольником называется фигура, которая состоит из трех точек, не лежащих на
А С
В
АВС
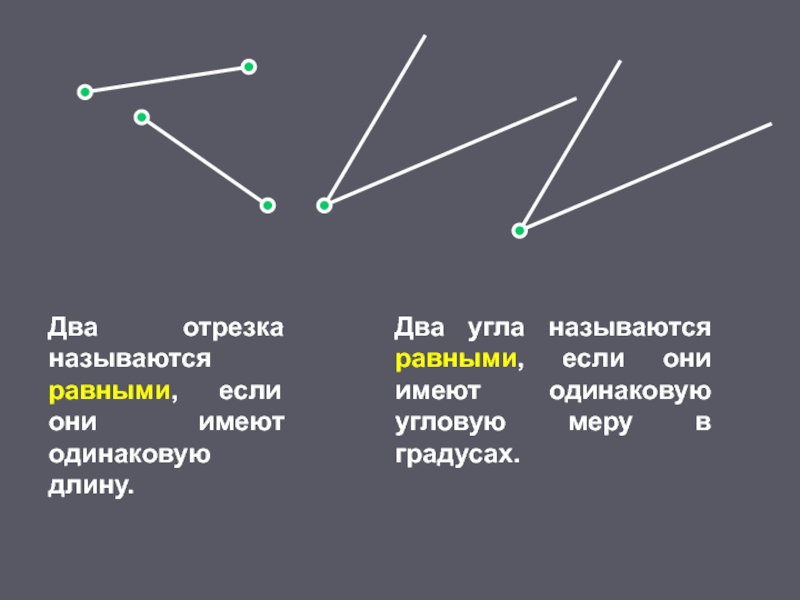
Слайд 21
Два отрезка называются равными, если они имеют одинаковую длину.
Два угла называются
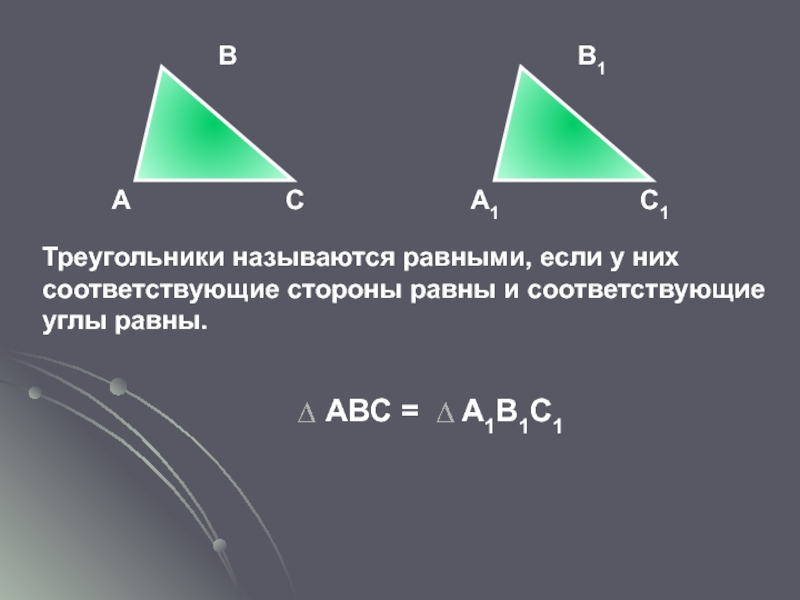
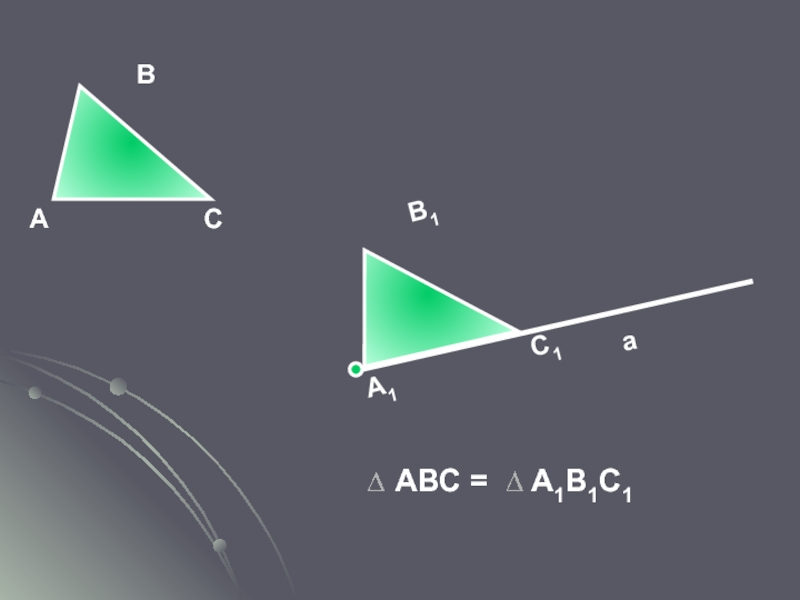
Слайд 22
А
В
А1 С1
В1
Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны.
АВС = А1В1С1
Слайд 23Основное свойство существования треугольника равного данному
VIII. Каков бы ни был
Существование треугольника равного данному
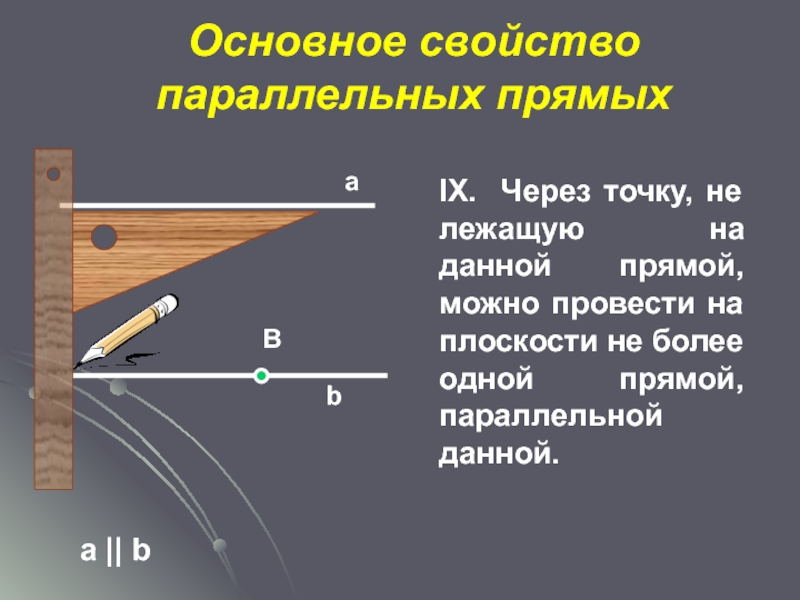
Слайд 26Основное свойство параллельных прямых
а || b
а
В
b
IX. Через точку, не лежащую на
Слайд 27В развитии геометрии важную роль сыграла аксиома, которая в «Началах…» Евклида
Много веков усилия большого числа ученых были направлены на доказательство этой аксиомы. Это объяснялось тем, что число аксиом стремились свести к минимуму. Ученые думали, что пятый постулат можно доказать как теорему, опираясь на остальные аксиомы.
В конце XVIII в. у некоторых геометров возникла мысль о невозможности доказать V постулат. Решение этого вопроса было найдено великим русским математиком Николаем Ивановичем Лобачевским (1792-1856 гг).
Лобачевский предпринял попытку доказать это утверждение от противного: он предположил, что через точку, не лежащую на данной прямой можно провести несколько прямых, не пересекающих данную.
Слайд 28Лобачевский не получил противоречивых выводов. На основании этого им был сделан
Сообщение об открытии новой геометрии было сделано Лобачевским в 1826 г.
Современной наукой установлено, что евклидова геометрия лишь приближенно, хотя и с очень большой точностью, описывает окружающее нас пространство, а в космических масштабах она имеет заметное отличие от геометрии реального пространства. Бурное развитие математики в XIX в привело к созданию выдающимся немецким математиком Б.Риманом (1826-1866 г.г) новой геометрии.
Слайд 29Аксиомы.
Теоремы и доказательства
Утверждения, принимаемые без доказательств,
Утверждение, истинность которого необходимо доказать, называется теоремой.
Доказательство – это рассуждения, опирающееся на аксиомы и ранее доказанные теоремы, устанавливающее истинность данного факта. Никакими другими свойствами фигур, даже если они нам кажутся очевидными, пользоваться нельзя.
При доказательстве разрешается пользоваться чертежом как геометрической записью того, что мы выражаем словами.
Определение – словесное описание геометрического объекта, объясняющее, что это такое.
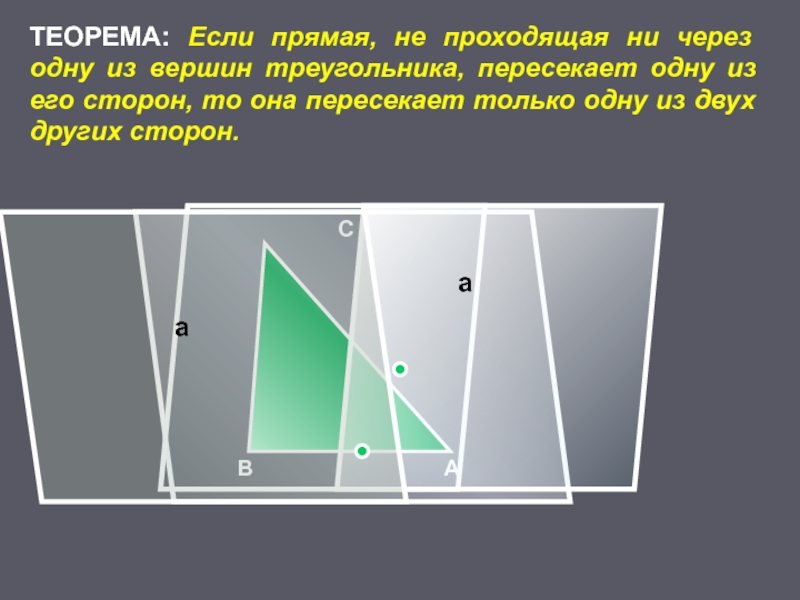
Слайд 30
ТЕОРЕМА: Если прямая, не проходящая ни через одну из вершин треугольника,
В А
С
а
а