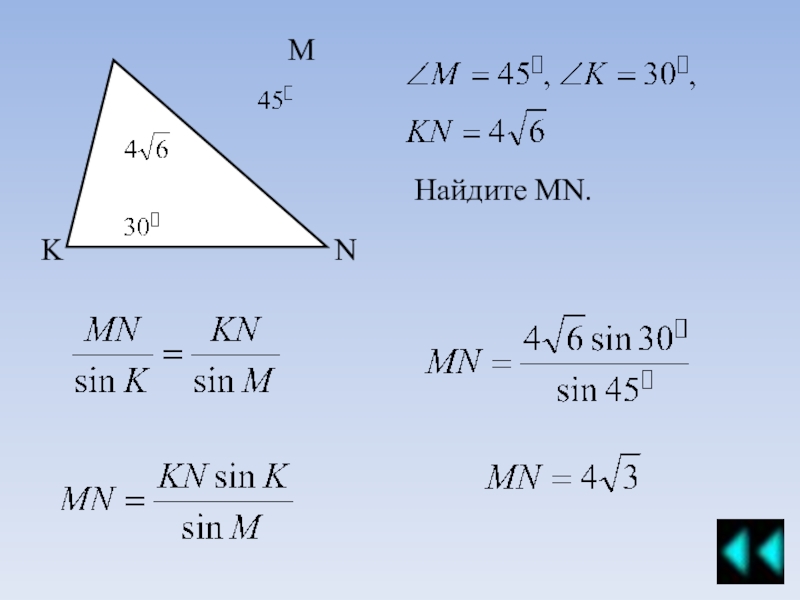Презентация, доклад на тему Мастер-класс. Учись решать задачи по геометрии по теме Треугольники. Подготовка к ОГЭ

теме «ТРЕУГОЛЬНИКИ»

Главная

Введение

Что это такое?

История

Справочные материалы

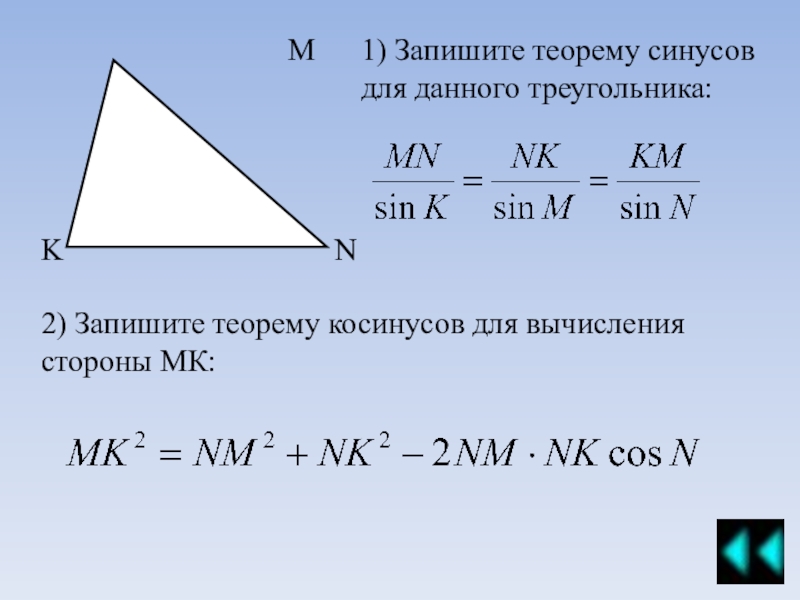
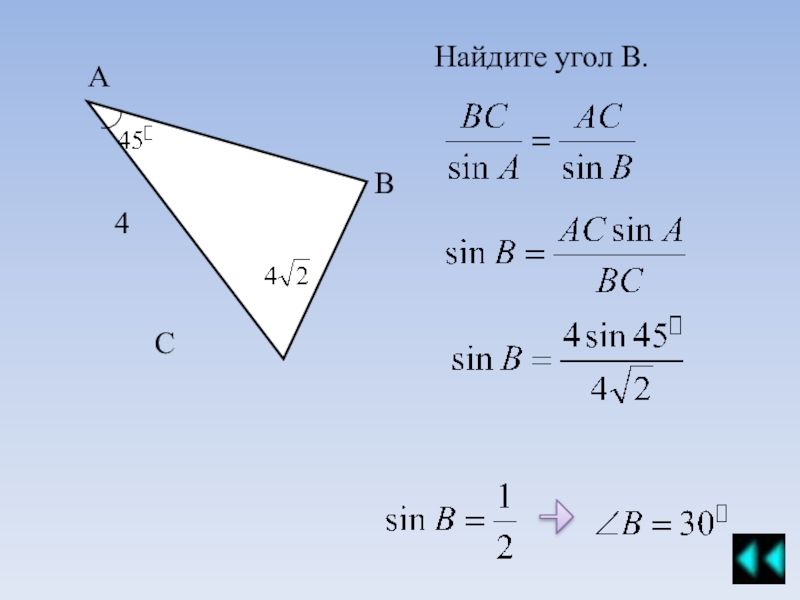
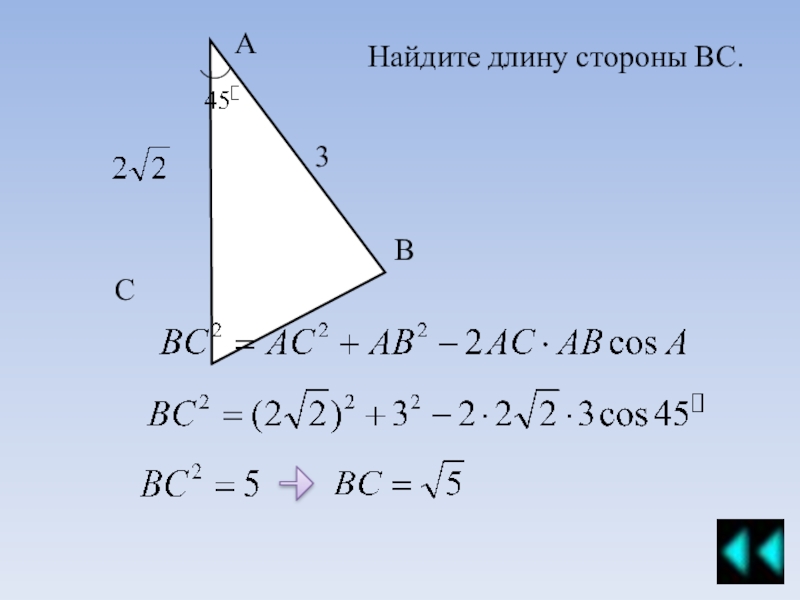
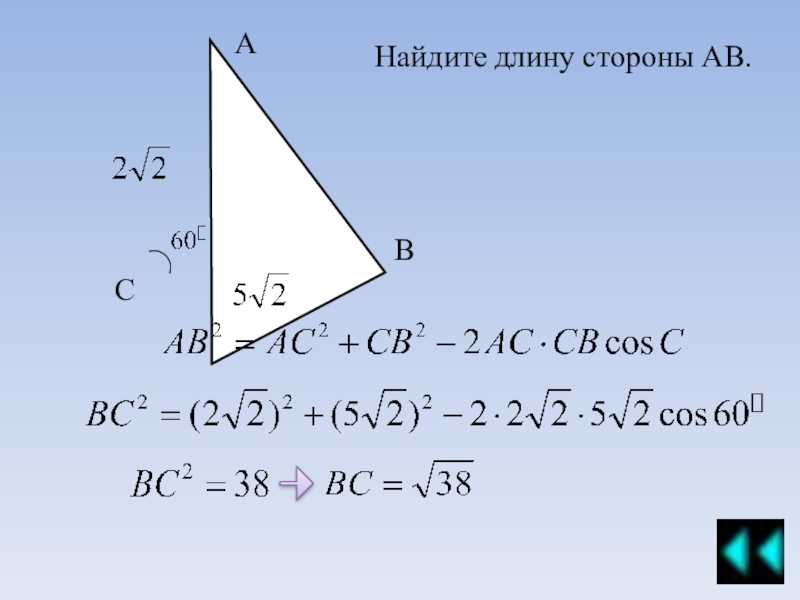
Примеры решения задач теорема Синусов, Косинусов

Итоги

Задачи для самостоятельного решения

Проверь себя

Предмет: ГЕОМЕТРИЯ
Тема: ТРЕУГОЛЬНИКИ
Учитель: Андреева С.Г.
МБОУ «Солодчинская СШ»

Критерии оценок

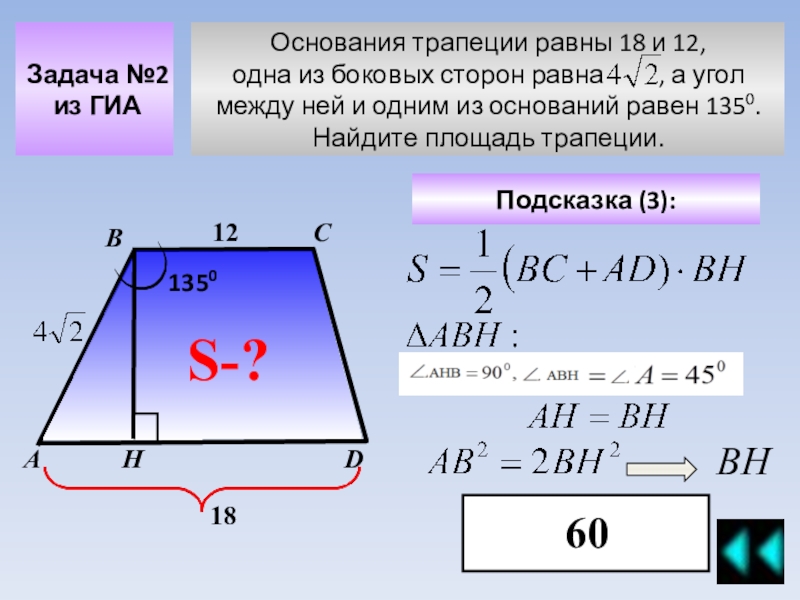
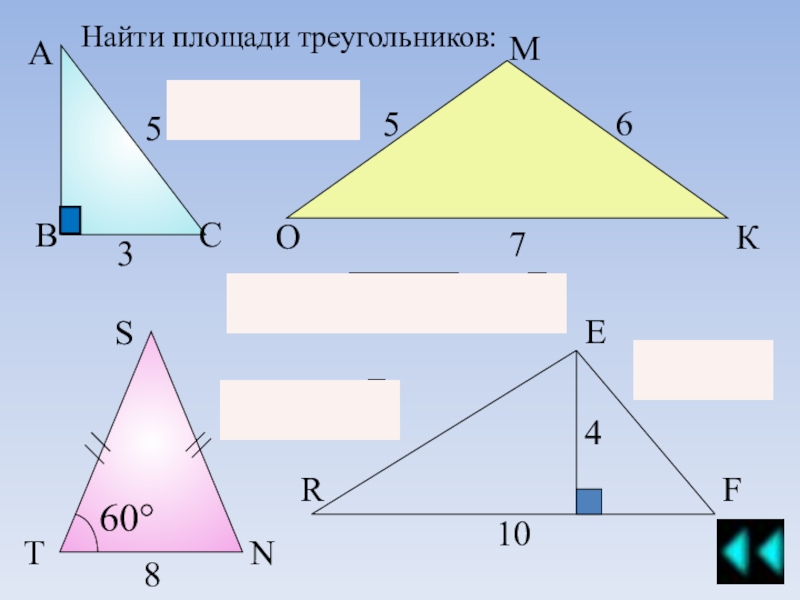
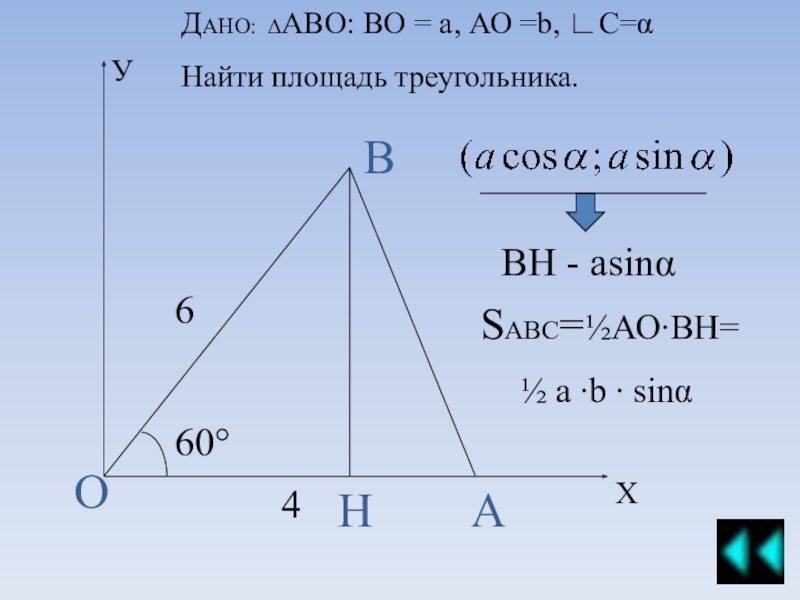
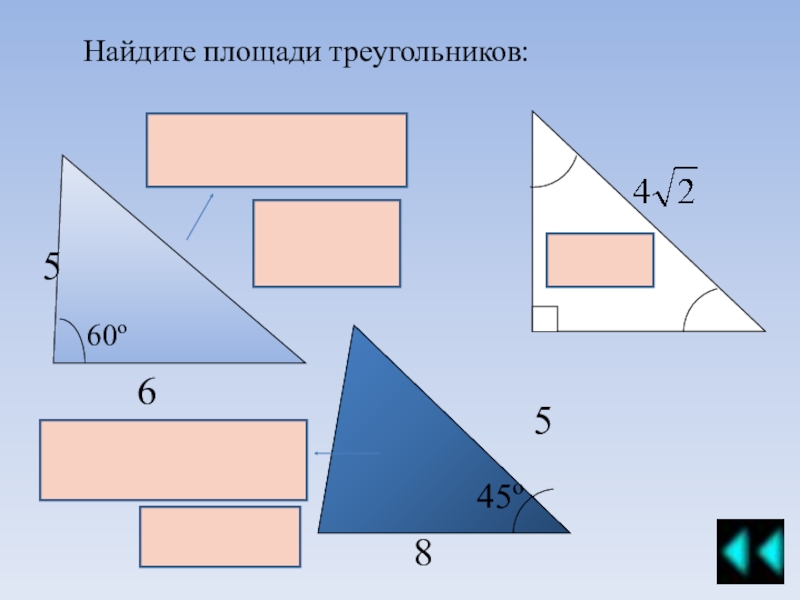
Примеры решения задач площадь треугольника

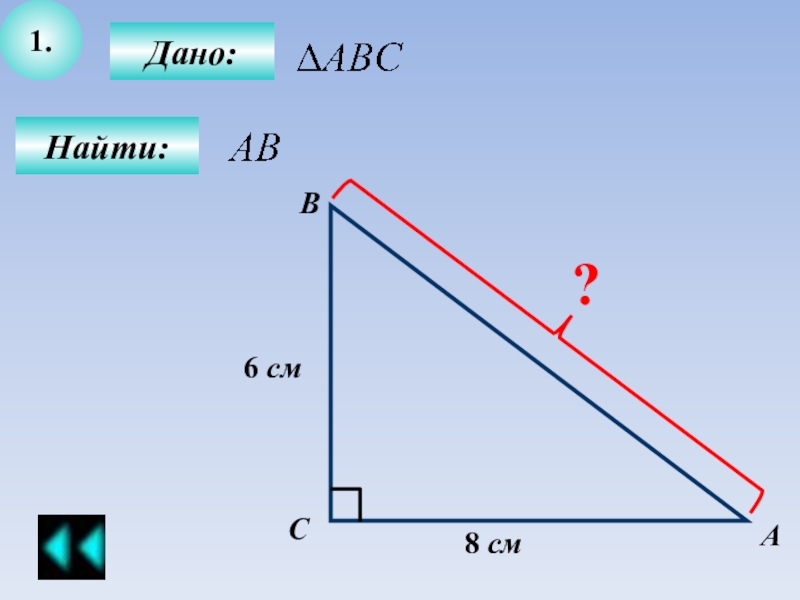
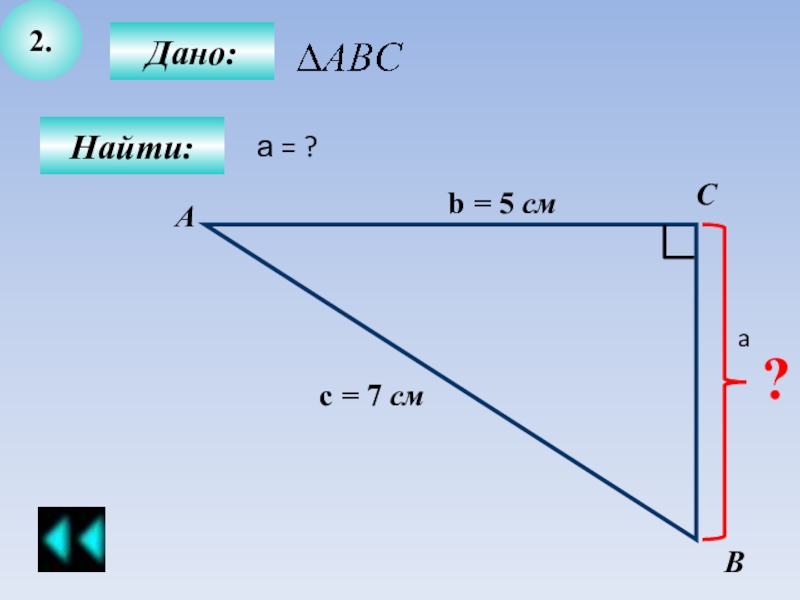
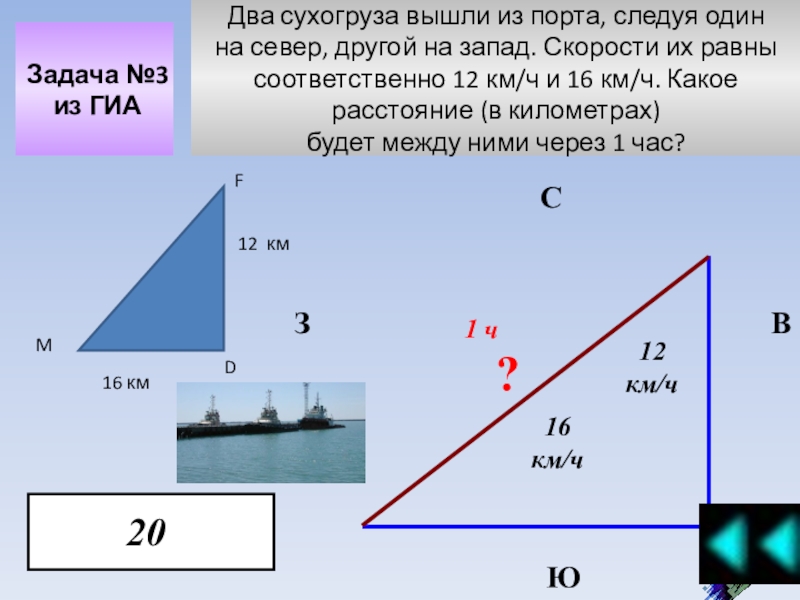
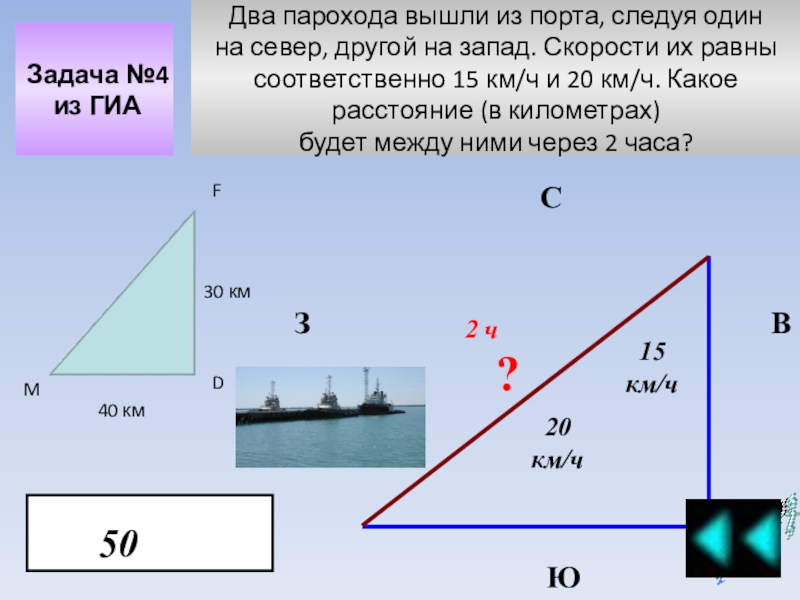
Примеры решения задач теорема Пифагора

классе по математике разделен на 3 модуля: алгебра, геометрия и реальная математика. В модуль геометрия входят различные задания, при выполнении которых необходимы знания и умения решать задачи по темам, связанным с такой фигурой, как треугольник.
Вы имеете возможность самостоятельно повторить и прорешать задачи по этой теме. Предложенный квест – это самоучитель, который снабжен необходимым справочным материалом для решения задач.
С помощью квеста вы сможете подробно разобрать приведенные примеры и проверить себя с помощью предложенной схемы решения.
Подробно изучив предложенный материал, вам предстоит самостоятельно решить предложенные задачи.
Объединитесь в группы и начните изучение предложенной темы с помощью карты квеста.

фигура, состоящая из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки – это вершины, а отрезки – стороны.

Треугольники бывают
остроугольные, прямоугольные, тупоугольные
равнобедренные, равносторонние

из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.

Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору, строгое аксиоматическое доказательство утверждения принадлежит Евклиду.

Также может быть выражена как геометрический факт равенства площади треугольника, отложенного гипотенузы с суммой площадей треугольников, отложенных от катетов. Верно и обратное утверждение: треугольник, сумма квадратов длин двух сторон которого равна квадрату длины третей стороны, является прямоугольным.
По мнению историка математики Морица Кантора в Древнем Египте во времена царя Аменемхета I (около XXIII век до н. э.) было известно о прямоугольном треугольнике со сторонами 3, 4, 5 — его использовали гарпедонапты — «натягиватели верёвок». В древневавилонском тексте, относимом ко временам Хаммурапи (XX век до н. э.), приведено приближённое вычисление гипотенузы. По мнению Ван-дер-Вардена, очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.
Общепринято, что доказательство соотношения дано древнегреческим философом Пифагором (570—490 до н. э.). Имеется свидетельство Прокла (485—410 до н. э),
что Пифагор использовал алгебраические методы,
чтобы находить пифагоровы тройки.

в треугольнике равна 180 градусов!
c ^2 =a^2 +b^2 Теорема Пифагора

— это сторона,
Лежащая напротив прямого угла.
Катеты — стороны, лежащие
напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе.
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе.
Тангенс острого угла в прямоугольном треугольнике —
отношение противолежащего катета к прилежащему.

Критерии оценок

решение задач самостоятельной работы .
Проведите рефлексию, используя раздел «Критерии оценок».

Критерии оценок

Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

верные.

В любой прямоугольный треугольник можно вписать окружность.
Каждая сторона треугольника больше суммы двух других сторон.
Существует треугольник ABC с меньшей стороной AC и углами ∠A=43 ∘ , ∠C=72 ∘ .
Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.
Любые два равнобедренных треугольника подобны.
Центр окружности, описанной около прямоугольного треугольника, находится на катете этого треугольника.
Если стороны одного треугольника соответственно в 3 раза больше сторон другого, то треугольники подобны.
8. Треугольник, стороны которого равны 7, 12, 13 является прямоугольным.

Критерии оценок

Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

оценок

Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

оценок

Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

пересечения его высот.
Треугольник, стороны которого равны 7, 12, 13 является прямоугольным.
Любые два прямоугольных треугольника подобны.
Центром окружности, вписанной в правильный треугольник, является точка пересечения серединных перпендикуляров к его сторонам.
В треугольнике против меньшего угла лежит меньшая сторона.
Внешний угол треугольника равен сумме внутренних, не смежных с ним.
Существует треугольник с двумя равными тупыми углами. Медиана треугольника делит треугольник на два равных.

Критерии оценок

Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

его площадь.
Если в треугольнике равны два угла, то он равнобедренный.
Биссектриса угла треугольника делит сторону треугольника пополам.
В равностороннем треугольнике все углы равны.
Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны.
Центр окружности, вписанной в равнобедренный треугольник, находится в точке пересечения его высот.
Все треугольники со сторонами 3, 4, 5 равны между собой.
Если в треугольнике два угла равны, то треугольник равнобедренный.
Ни в каком треугольнике не может быть два тупых угла.

Критерии оценок

Учусь решать задачи по теме «ТРЕУГОЛЬНИКИ»

решать задачи по теме «ТРЕУГОЛЬНИКИ»

вычисления стороны МК:

по теме «ТРЕУГОЛЬНИКИ»

запад. Скорости их равны
соответственно 12 км/ч и 16 км/ч. Какое
расстояние (в километрах)
будет между ними через 1 час?

Задача №3
из ГИА

С

В

З

Ю

?

12 км/ч

16 км/ч

1 ч

20

F

D

M

12 км

16 км

, а угол
между ней и одним из оснований равен 1350.
Найдите площадь трапеции.

Задача №2
из ГИА

С

D

А

В

Подсказка (3):

60

S-?

12

18

1350

Н

ВН

запад. Скорости их равны
соответственно 15 км/ч и 20 км/ч. Какое
расстояние (в километрах)
будет между ними через 2 часа?

Задача №4
из ГИА

С

В

З

Ю

?

15 км/ч

20 км/ч

2 ч

50

F

D

M

30 км

40 км

задачи по теме «ТРЕУГОЛЬНИКИ»

аsinα

SABC=½АО∙ВН=
½ а ∙b ∙ sinα

самостоятельно, используя чертежи и определение тангенса угла.

Критерии оценок

Най­ди­те тан­генс угла AOB, изоб­ра­жен­но­го на ри­сун­ке.

Най­ди­те тан­генс угла, изоб­ра­жен­но­го на ри­сун­ке.

оценок

Итоги

Объединитесь в группы, изучите справочные материалы.
Войдите в раздел «Примеры решения задач» и начинайте изучать решение задач. Выполните задание из раздела «Проверь себя».
Теперь вы готовы к решению основных типов задач, встречающихся в ГИА – 9 по математике из раздела геометрия.
Если все получилось, переходите к разделу «Задачи для самостоятельного решения».
Как подвести итоги, вы найдете в разделе «Итоги».