- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Квадрат теңдеулердің шешу әдістері
Содержание
- 1. Квадрат теңдеулердің шешу әдістері
- 2. 1. квадрат теңдеулер түбірлерін табу тұралы
- 3. Сабақтын түрі: аралас
- 4. Мұғалімнің кіріспе сөзіҚұрметті оқушылар! Мен сендер мен
- 5. ӘдебиеттерҚортындыЗерттеу әдісіМетодикалық негізМіндеттерМақсатГипотезаПроблема
- 6. Осы сабаққа, біз алдын ала дайындалдық, үш
- 7. ТеоретиктарТапсырма: Анаграмманы шешу1. т а н и
- 8. Слайд 8
- 9. Слайд 9
- 10. «Теңдеу дегеніміз, барлық математикалық құпияны ашатын алтын кілт». С. Коваль.
- 11. Ен алдымен өткен тақырыпты қайталайық: 1. Екінші
- 12. Слайд 12
- 13. Квадрат теңдеудің Энциклопедиясы
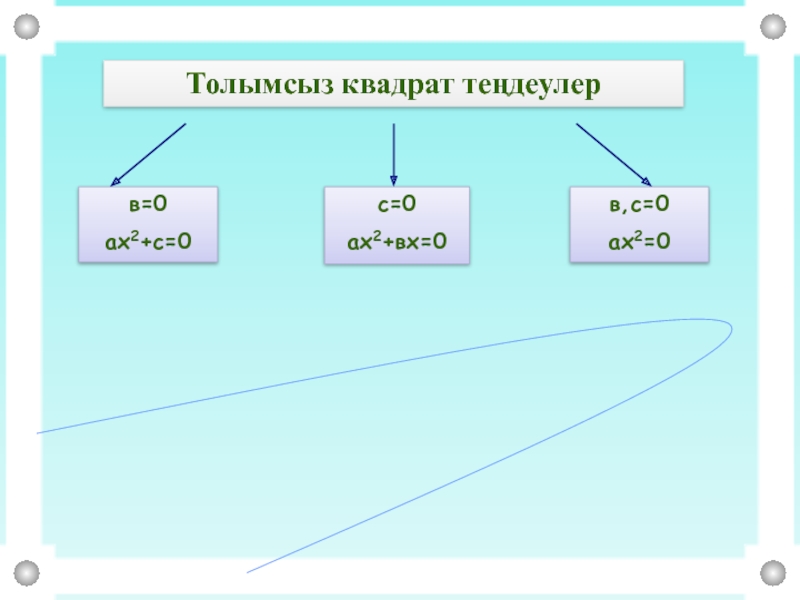
- 14. Толымсыз квадрат теңдеулерв=0ах2+с=0с=0ах2+вх=0в,с=0ах2=0
- 15. Шешу алгоритмі 1. с – ні теңдеудің
- 16. x-і жақшаның сыртына шығарамыз:
- 17. 1. Теңдеудің екі жағын а-ға бөлеміз а≠0.х2 = 02. Бір шешім: х = 0.в,с=0ах2=0Шешу алгоритмі
- 18. Толымсыз квадрат теңдеулер :
- 19. D < 0D = 0D > 0Түбірі жоқ
- 20. b = 2k (жұп сан)
- 21. Виет теоремасы x1 , х2
- 22. Зерттеу жолы Теоретик: Біз өткен тақырыпты
- 23. Жалпы әдістер:Көбейткіштерге жіктеу;Жаңа айнымалыны еңгізу;График әдісі.Дискриминант арқылыВиет теоремасы
- 24. Арнайы әдістер:1. Екі мүшенің квадратын айыру әдісі.2. Асыра лақтыру әдісі.3. Қоэффициентер қассиет бойынша.
- 25. Талдаушылар:Біздің алгоритмге сәйкесінші гипотезаны аңықтап, тексеруіміз керек.
- 26. Әдістің мәні:
- 27. (a + b)2 = a2 +
- 28. Квадрат теңдеулердің түбірлері және ара қатынастармен байланыстыжәнеМысал: «Асыра лақтыру» әдісі.2х2 - 9х – 5 = 0.
- 29. ax2 + bx + c =
- 30. Теорема бойынша: Егер квадрат теңдеуде a+b+c=0, онда
- 31. Теорема 1. Егер квадрат теңдеуде a +
- 32. Теорема 2. Егер квадрат теңдеуде a
- 33. ҰБТ есептерін шешіп тексерейік: есеп шешу барысында
- 34. Теңдеуді шеш: A) 0,6.
- 35. Слайд 35
- 36. Слайд 36
- 37. Қорытынды: Сонымен теңдеудің түбірін табудын тағы үш
- 38. Шешуі: х- үйірдегі маймыл саны,
- 39. Үй тапсырмасы: № 159,160
- 40. Осы әдістер, алдымыздағы
- 41. Назарларыңызға рахмет!!!
Слайд 2 1. квадрат теңдеулер түбірлерін табу тұралы түсініктерін толықтыру, түбірлер мен коэффициенттер
Мақсаты:
Слайд 3 Сабақтын түрі: аралас сабақ Қолданатын технология: “жоба әдісі”
Слайд 4Мұғалімнің кіріспе сөзі
Құрметті оқушылар! Мен сендер мен бірге сабақ өткізуге қуаныштымын.
Сабақ кезені:
Слайд 6Осы сабаққа, біз алдын ала дайындалдық, үш топқа бөліндік: “теоретиктар”, “талдаушылар”,
Слайд 7Теоретиктар
Тапсырма: Анаграмманы шешу
1. т а н и и м д к
е д ң у е т (теңдеу)
ф э к о ц и н е т и ф (коэффициент)
Үрбті (түбір)
Осы сөздер қандай таққырыппен байланысты? (квад.теңд)
Тақырып: Квадрат теңдеулерді шешу
Мақсаты: Квадрат теңдеулердің рацинал шешу жолдарын анықтау, оларды ҰБТ тапсырмаларын шешуге қолдануын.
Міндеттер: жаңа әдістерді және жалпы әдісті қолданып тест тапсырмаларын шешу, осы әдістерді салыстыру, энциклопедия шығару.
Слайд 8
.
Сіздер білесіздерме «Квадрат теңдеу» деген аталымды ең бірінші еңгізген неміс философы
неміс философы, 1679 ж. Бреславла қаласында кәсіпші жанұясында дүниеге келген, ол - Йена қаласында дінтануды, одан кейін, математика мен философияны оқыды.
Кристиан Вольф.
Кристиан Вольф - - атақты
Слайд 11Ен алдымен өткен тақырыпты қайталайық: 1. Екінші дәрежелі теңдеуді қалай атаймыз? Оның
Слайд 15Шешу алгоритмі
1. с – ні теңдеудің он жағына көшіреміз
ах2
2. Теңдеудің екі жағын а-ға бөлеміз, а≠0.
х2= .
3.Егер >0 – онда екі шешім:
х1 = и х2 = -
Егер < 0 – шешімі жоқ.
в=0
ах2+с=0
Слайд 16
x-і жақшаның сыртына шығарамыз:
х (ах + в)
2. Теңдеудің екі көбейткішін бөлек қарастырамыз:
x = 0, ах + в = 0.
3. Екі шешім:
х = 0 и х = (а≠0).
Шешу алгоритмі
с=0
ах2+вх=0
Слайд 22Зерттеу жолы
Теоретик: Біз өткен тақырыпты есімізге алдық.Ал қалай ойлайсыздар тағы
Мұғалім: Міне, мәселі қойылды. Қойған сұраққа жауап берейік.
Оқушылар: Иә. Тағыда , біз білмейтің әдістер бар шығар
Теоретик: : Квадрат теңдеулер шешуінің 10 әдісі бар:
Виет теорема бойынша 6.номограмма көмегімен
Дискриминант бойынша. 7. линейка және циркульмен
Коэффициентер қасиет 8. Толық квадратты айыру
бойынша 9. көбеткіштерге жіктеу
4. «Асыра лақтыру» әдісі 10. Безу теоремасы
5. График әдісі бойынша
Слайд 23Жалпы әдістер:
Көбейткіштерге жіктеу;
Жаңа айнымалыны еңгізу;
График әдісі.
Дискриминант арқылы
Виет теоремасы
Слайд 24Арнайы әдістер:
1. Екі мүшенің квадратын айыру әдісі.
2. Асыра лақтыру әдісі.
3. Қоэффициентер
Слайд 25Талдаушылар:Біздің алгоритмге сәйкесінші гипотезаны аңықтап, тексеруіміз керек. Гипотеза: арнайы әдістерді қолданғанда, теңдеулерді
Слайд 26
Әдістің мәні: жалпы түріндегі квадрат теңдеуді,
Мысал: х2 - 6х + 5 = 0.
Екі мүшенің квадратын айыру әдісі.
Слайд 27
(a + b)2 = a2 + 2ab + b2,
(a
Теңдеудің шешуі: х2 - 6х + 5 = 0.
(х -3)2 – 4 = 0.
(х -3)2 = 4.
х – 3 = 2; х – 3 = -2.
х = 5, х =1.
Жауабы: 5; 1.
Слайд 28Квадрат теңдеулердің түбірлері
және
ара қатынастармен байланысты
және
Мысал:
«Асыра лақтыру» әдісі.
2х2 -
Слайд 29
ax2 + bx + c = 0 және y2+ by
Қатынастармен байланысты
Теңдеуді шеш: 2х2 - 9х – 5 = 0.
у2 - 9у - 10 = 0.
D>0, Виета терема арқылы, тұбірлері: -1; 10,
Содан кейін алғашқы теңдеудің түбірлерін табамыз : - 0,5; 5.
Жаубы: 5; -0,5.
Слайд 30 Теорема бойынша:
Егер квадрат теңдеуде a+b+c=0, онда түбірдің бірі тең 1,
Виет теорема бойынша тең
Егер квадрат теңдеуде a-b+c=0, онда түбірдің бірі тең -1, ал екіншісі
Виет теорема бойынша тең
Мысал:
200х2 + 210х + 10 = 0.
Слайд 31Теорема 1. Егер квадрат теңдеуде a + c – b=0, онда
Теңдеуді шеш: 200х2 + 210х + 10 = 0.
a = 200, b = 210, c = 10.
a + c- в = 200 + 10 - 210= 0.
х1 = -1, х2 = -
Жауабы: -1; -0,05
Слайд 32Теорема 2. Егер квадрат теңдеуде a + b + c =
Теңдеуді шеш: 137х2 + 20х – 157 = 0.
a = 137, b = 20, c = -157.
a + b+ c = 137 + 20 – 157 =0.
x1 = 1,
Жауабы: 1; .
.
Слайд 33ҰБТ есептерін шешіп тексерейік: есеп шешу барысында оқушы жалпы әдіске және
Практиктер
Слайд 37Қорытынды: Сонымен теңдеудің түбірін табудын тағы үш түрін үйрендік.Квадрат теңдеуге байланысты