- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему История преподавания геометрии. Полезная презентация по мотивам интернет материалов
Содержание
- 1. История преподавания геометрии. Полезная презентация по мотивам интернет материалов
- 2. Первый учебник по геометрииСистема светского государственного образования
- 3. Проявилась характерная тенденция, которая определила обучение геометрии
- 4. По планиметрии изучаются: учение об отрезках, о
- 5. По стереометрии рассматриваются начала параллельности и перпендикулярности
- 6. Первая книга начинается с 23 определений1. Точка
- 7. Затем идут постулаты. Требуется, чтобы… I.
- 8. Наконец, аксиомы. Равные порознь третьему равны между
- 9. Заметим, что у Евклида есть аксиомы и
- 10. «Сборник геометрических задач» В. П. Минина Задача
- 11. С. И. Шохор-Троцкий (начало 20 в.) придавал
- 12. Передовой дореволюционный опыт долгое время не использовался,
- 13. А.М. Пышкало: уровни геометрического развитияI. Исходный уровень
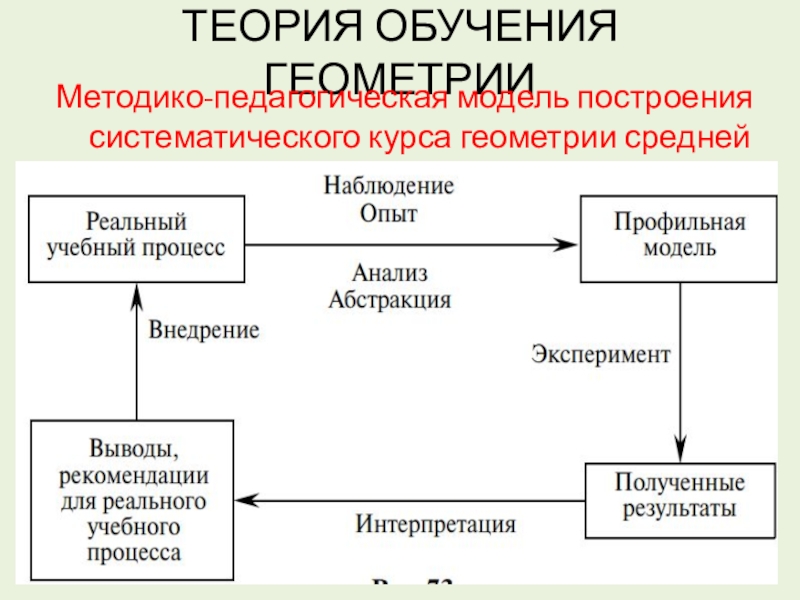
- 14. ТЕОРИЯ ОБУЧЕНИЯ ГЕОМЕТРИИМетодико-педагогическая модель построения систематического курса геометрии средней школы
- 15. Цели обучения геометрии в школеВыделяются два основных
- 16. Слайд 16
- 17. Э л е м е н т
- 18. В качестве примера рассмотрим задачу по теме
- 19. Лабораторные работыI. Планиметрия 1. Построение геометрических мест
- 20. Лабораторные работыII. Стереометрия 1. Изображение пространственных фигур
Слайд 1Преподавание геометрии
«Я думаю, что никогда
до настоящего времени
Мы не жили
Все вокруг — геометрия»
Ле Корбюзье
Слайд 2Первый учебник по геометрии
Система светского государственного образования стала складываться в России
Первой реформой, с которой начал царь, была реформа образования. Одной из первых школ нового типа была открытая в 1701 г. в Москве знаменитая школа «математических и навигацких, т. е. мореходно хитростных наук». Помещалась она в Сухаревской башне (снесенной в тридцатых годах двадцатого столетия). Среди предметов математического цикла изучались: арифметика, алгебра, геометрия, тригонометрия — плоская и сферическая. В качестве учебника по геометрии использовалась историческая книга «Начала» Евклида [52]. Ее перевод был сделан Фарварсоном. Это англичанин, известный профессор Аббердинского университета, который был приглашен Петром I в «навигацкую» школу для преподавания математики и морских наук.
Слайд 3Проявилась характерная тенденция, которая определила обучение геометрии в России приблизительно до
Эта книга в то время считалась непревзойденным образцом изложения геометрии, а потому по ней велось обучение в различных школах. «Начала» были написаны Евклидом около 300 г. до н. э. Они состоят из 13 основных книг.
Первые шесть
(книги I—VI) посвящены планиметрии;
VII—IX — арифметике;
X — несоизмеримым отрезкам
и XI—XIII — стереометрии.
Слайд 4По планиметрии изучаются:
учение об отрезках, о сторонах и углах треугольника;
построение треугольников, перпендикулярных и параллельных прямых на плоскости;
параллелограммы;
площади треугольников и параллелограммов;
теорема Пифагора.
учение об окружности и круге;
о секущих и касательных; об углах, образуемых ими;
о вписанных и описанных многоугольниках.
построение правильных многоугольников: четырехугольник, пятиугольник, шестиугольник и 15-угольник.
Дается понятие подобных фигур.
Слайд 5По стереометрии рассматриваются
начала параллельности и перпендикулярности в пространстве,
определяется отношение
дается теория правильных многогранников.
Это выдающееся произведение положило начало дедуктивному способу изложения, который заключается в том, что п
режде всего дается перечень основных понятий и всех аксиом.
Затем формулируются теоремы и для каждой из них приводится доказательство, даются определения всех вновь вводимых понятий.
Слайд 6Первая книга начинается с 23 определений
1. Точка есть то, что не
2. Линия есть длина без ширины.
3. Границы линии суть точки.
4. Прямая есть линия, которая одинаково расположена относительно всех своих точек.
5. Поверхность есть то, что имеет только длину и ширину.
6. Границы поверхности суть линии.
7. Плоскость есть поверхность, которая одинаково расположена по отношению ко всем прямым, на ней лежащим.
8. Угол есть взаимное наклонение двух встречающихся линий, расположенных в одной плоскости, но не расположенных на одной прямой. …
23. Параллельные суть прямые, которые, находясь в одной плоскости и будучи продолжены в обе стороны неограниченно, ни с той, ни с другой стороны между собой не встречаются.
Слайд 7Затем идут постулаты.
Требуется, чтобы…
I. Чтобы из каждой точки ко
II. И чтобы каждую неограниченную прямую можно было продолжать неограниченно.
III. И чтобы из каждой точки, как из центра, можно было произвольным радиусом описать окружность.
IV. И чтобы все прямые углы были равны друг другу.
V. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых.
Слайд 8Наконец, аксиомы.
Равные порознь третьему равны между собой.
II. И если
III. И если от равных отнимем равные, то получим равные. I
V. И если к неравным прибавим равные, то получим неравные.
V. И если удвоим равные, то получим равные.
VI. И половины равных равны между собой.
VII. И совмещающиеся (величины, образы) равны между собой.
VIII. И целое больше части.
IX. И две прямые линии не могут заключить пространства.
Слайд 9Заметим, что у Евклида есть аксиомы и постулаты.
Первые — утверждения,
В то время как постулаты — это требования, с которыми можно соглашаться или не соглашаться.
Например, Н. И. Лобачевский не согласился с V постулатом Евклида («Через точку, не принадлежащую прямой, проходит не более одной прямой, параллельной данной»), и была открыта неевклидова геометрия.
Исходя из этого, Евклид развил и представил геометрическую теорию, все доказывая логическим путем, без ссылок на наглядность и очевидность.
Эта книга оказала огромное и длительное (почти 2000 лет) влияние на науку и культуру цивилизованных народов. По ней изучали математику Н. Коперник, Г. Галилей, Р. Декарт, И. Ньютон, Г. Лейбниц, Л. Эйлер, М. В. Ломоносов, Н. И. Лобачевский и многие другие выдающиеся ученые. О значении этой книги можно судить, например, по следующему высказыванию известного итальянского математика XVI в. Д. Кардано: «Неоспоримая крепость их догматов и их совершенство настолько абсолютны, что никакое другое сочинение по справедливости нельзя с ними сравнивать. В них отражается такой свет истины, что, по-видимому, только тот способен отличать в сложных вопросах геометрии истинное от ложного, кто усвоил Евклида».
Слайд 10«Сборник геометрических задач» В. П. Минина
Задача № 541 (отдел 10).
Из шара, составленного из железного и медного полушарий и весящего P килограммов, выпиливается куб, диагональ которого равна диаметру шара. Определить вес опилок.
Пример экзаменационной геометрической задачи на аттестат зрелости для учащихся Московского учебного округа (испытания 1873 г.).
З а д а ч а № 877 Сторона десятиугольного основания правильной пирамиды равна 0,93 арш., апофема пирамиды равна 25 арш. Определить поверхность и объем описанного около пирамиды конуса, усеченного параллельно основанию, при этом дано, что сечение сделано на расстоянии высоты от основания. (Напомним, что 1 аршин = 71,1 см.)
Слайд 11С. И. Шохор-Троцкий (начало 20 в.) придавал огромное значение наглядности в
Обучая математике, должно иметь в виду не только способность человека к умозрению, но и органы ощущений учащихся и волевой элемент в душевной их жизни.
Без чувственных восприятий и соответствующих им ощущений и представлений не может получиться ни точных понятий, ни плодотворных математических идей, ни основательных знаний, ни твердых навыков.
Одно только знание ряда слов без полной власти над их смыслом — знание призрачное, ложное и безрезультатное.
Истинное знание возможно только при следующих условиях: а) при наличии ясных и верных представлений; б) при должной подготовке к надлежащему ассоциированию представлений и идей, составляющих материал этого знания.
Эти условия достижимы только при полной наглядности обучения, при интересе детей к делу и при посильной активной работе органов ощущений, с одной стороны, и ума, творческой фантазии и воли — с другой.
6) Готовые наглядные пособия, конечно, полезны, но важнее всего самодеятельность учеников, а потому изготовленные ими самими наглядные пособия и затраченный при этом планомерный физический труд еще полезнее, чем готовые наглядные пособия.
Слайд 12Передовой дореволюционный опыт долгое время не использовался, только сейчас начинается возрождение
А связующим звеном между прошлым и настоящим являются две значительные работы: П. А. Карасева и А. М. Пышкало.
Автор первой работы считал, что, в отличие от геометрического материала в младших классах, «наглядная геометрия» (которую он называл также интуитивной) не должна быть придатком к арифметике, вырождаясь в изучение мер длины, площади и объема.
Им был разработан «наглядный метод»
изучения геометрии в младших классах,
в основу которого были положены «живое»
созерцание, конструирование, моделирование,
построения и измерения. Книга содержит
оригинальные упражнения, например с нитью,
листом бумаги, палочками и т. п.
Слайд 13А.М. Пышкало: уровни геометрического развития
I. Исходный уровень — характеризуется тем, что
фигуры воспринимаются как целое. Учащиеся не видят частей (элементов)
фигуры, не воспринимают отношений между элементами фигуры и фигурами.
II. Учащиеся начинают различать элементы фигур, устанавливать
отношения между этими элементами и отдельными фигурами, т. е.
на этом уровне производится анализ воспринимаемых фигур. Это
происходит в процессе (и с помощью) наблюдений, измерения,
вычерчивания, моделирования. Свойства фигур устанавливаются экспериментально.
III. Учащиеся устанавливают связи между свойствами фигуры и самими фигурами. На этом уровне происходит логическое упорядочивание свойств фигуры и самих фигур. Выясняется возможность следования одного свойства из другого; уясняется роль определения.
IV. Учащиеся постигают значение дедукции в целом как способа построения и развития всей геометрической теории. Переходу на этот уровень способствует усвоение учащимися (понимание ими) роли и сущности аксиом, определений, теорем; логической структуры доказательства; анализа логических связей понятий и предложений.
V. Этот уровень мышления в области геометрии соответствует современному (гильбертовскому) этапу строгости. На этом уровне достигается отвлечение от конкретной природы объектов и конкретного смысла отношений, связывающих эти объекты. Человек, мыслящий на таком уровне, развивает теорию вне всякой конкретной интерпретации.
Слайд 14ТЕОРИЯ ОБУЧЕНИЯ ГЕОМЕТРИИ
Методико-педагогическая модель построения систематического курса геометрии средней школы
Слайд 15Цели обучения геометрии в школе
Выделяются два основных направления в постановке курса
В соответствии с этим определяются следующие ц е л и обучения математике в школе:
а) овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
б) интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
в) формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
г) формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Слайд 17Э л е м е н т ы с о д
1. Термины (их запись, чтение, обозначение); понятия (не определяемые и определяемые).
2. Аксиомы, теоремы, задачи (среди которых мы выделяем устные, основные (базовые, стандартные), повышенной трудности, нестандартные, исследовательские, прикладные и практические, занимательные, исторические).
3. Классификации.
4. Теории.
5. Факты (исторические справки, дополнительные сведения).
Слайд 18В качестве примера рассмотрим задачу по теме «Четырехугольники» курса геометрии основной
1. Уровень выравнивания. Докажите, что середины сторон (выпуклого) четырехугольника являются вершинами параллелограмма. Докажите, что площадь полученного параллелограмма равна половине площади данного четырехугольника. Указание. Для решения задачи проведите какую-нибудь диагональ данного четырехугольника и рассмотрите образовавшиеся треугольники.
2. Базовый, основной уровень. Какой четырехугольник получится, если последовательно соединить середины сторон (выпуклого) четырехугольника? Найдите площадь получившегося четырехугольника, если площадь данного четырехугольника равна 16 см2.
3. Продвинутый уровень. Какой четырехугольник получится, если последовательно соединить середины сторон (выпуклого) четырехугольника? Найдите площадь получившегося четырехугольника, если площадь данного четырехугольника равна Q. В каком случае полученный четырехугольник будет: а) параллелограммом; б) прямоугольником; в) ромбом; г) квадратом?
4. Творческий уровень. Докажите, что точка пересечения отрезков, соединяющих середины противоположных сторон (выпуклого) четырехугольника, делит пополам отрезок, соединяющий середины диагоналей этого четырехугольника.
Слайд 19Лабораторные работы
I. Планиметрия
1. Построение геометрических мест точек.
2. Построение кривых:
3. Получение циклоидальных кривых: циклоиды, кардиоиды, астроиды.
4. Центральная симметрия.
5. Поворот.
6. Осевая симметрия.
7. Параллельный перенос.
8. Заполнение плоскости: равными четырехугольниками, правильными многоугольниками.
9. Задачи на разрезание (на плоскости).
10. Вычисление площадей плоских фигур.
Слайд 20Лабораторные работы
II. Стереометрия
1. Изображение пространственных фигур на плоскости.
2. Моделирование
3. Опыты с листом Мебиуса.
4. Каскадные модели последовательно вписанных друг в друга правильных многогранников.
5. Стереометрические фигуры из куска бумаги.
6. Заполнение пространства многогранниками
7. Задачи на разрезание (в пространстве).
8. Фигуры вращения.
9. Вычисление площади поверхности фигур вращения.
10. Вычисление объема фигур вращения.