- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Исследовательский проект Координатный метод решения геометрических задач
Содержание
- 1. Исследовательский проект Координатный метод решения геометрических задач
- 2. Цель Определить виды стереометрических задач из ЕГЭ профильного уровня и методы их решения. Задачи
- 3. Объект исследования: Стереометрические задачи. Предмет исследования: Методы решения стереометрических задач.
- 4. Планируемый результат: Определить наиболее рациональный метод решения стереометрических задач и научиться его применять.
- 5. Методы
- 6. Гипотеза: Координатный метод позволяет наиболее рационально
- 7. Алгебра - не что иное как записанная
- 8. Постановка проблемы Решить задачу: В правильной четырехугольной
- 9. Слайд 9
- 10. Основные понятияМетод координат — весьма эффективный и
- 11. Алгоритм применения метода координат к решению геометрических задач
- 12. Координаты многогранников
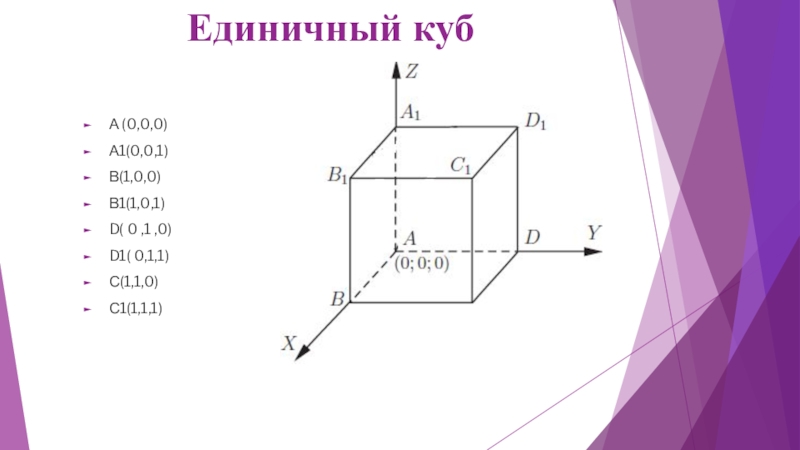
- 13. Единичный кубА (0,0,0) А1(0,0,1)В(1,0,0) В1(1,0,1) D( 0 ,1 ,0) D1( 0,1,1) С(1,1,0)С1(1,1,1)
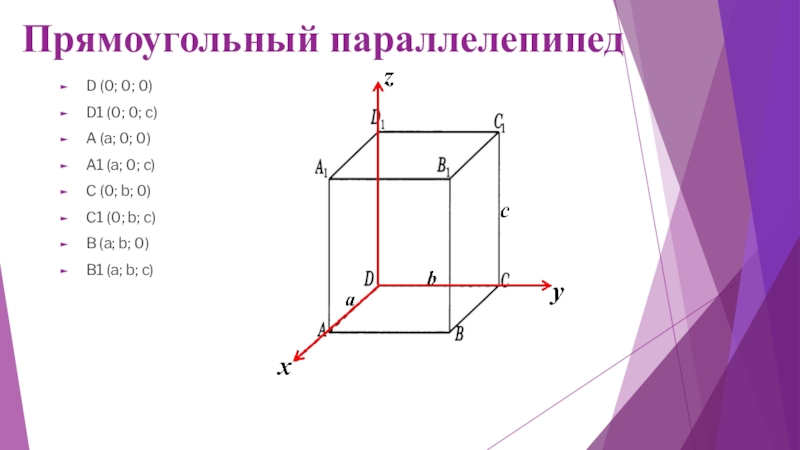
- 14. Прямоугольный параллелепипед D (0; 0; 0)D1 (0;
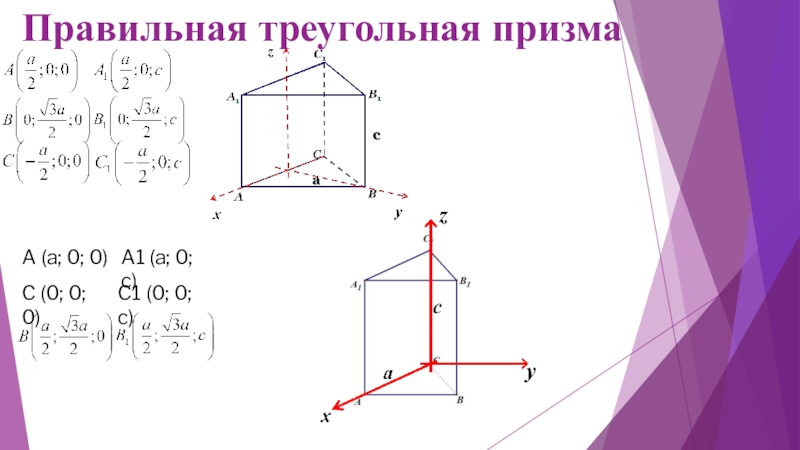
- 15. Правильная треугольная призмаA (a; 0; 0)A1 (a; 0; c)C (0; 0; 0)C1 (0; 0; c)
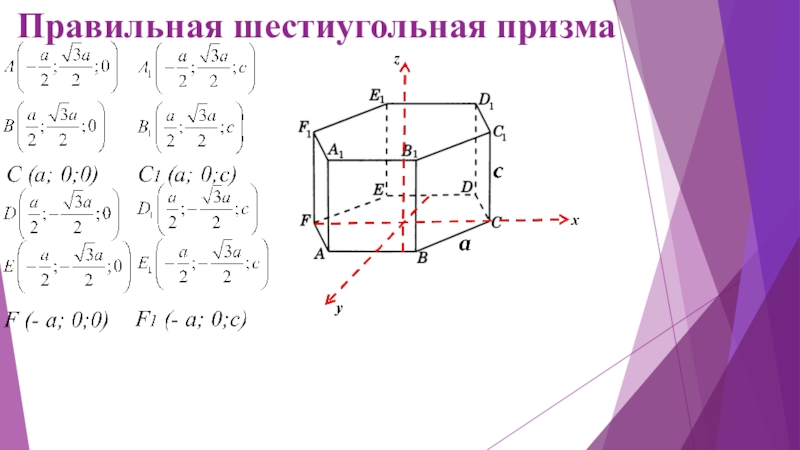
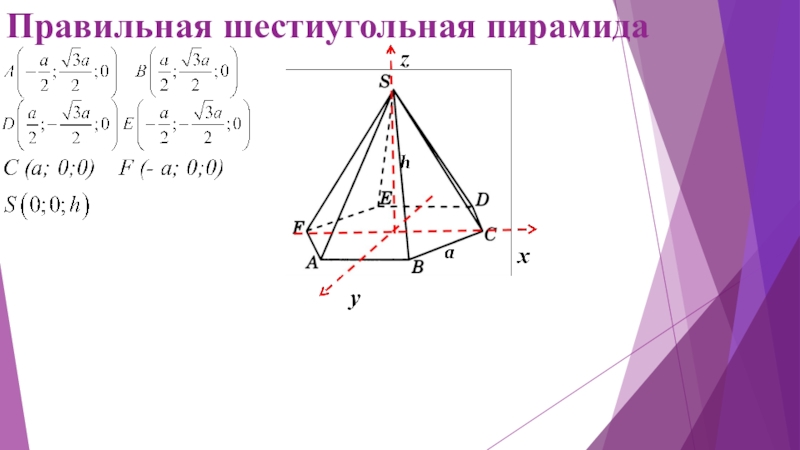
- 16. Правильная шестиугольная призма
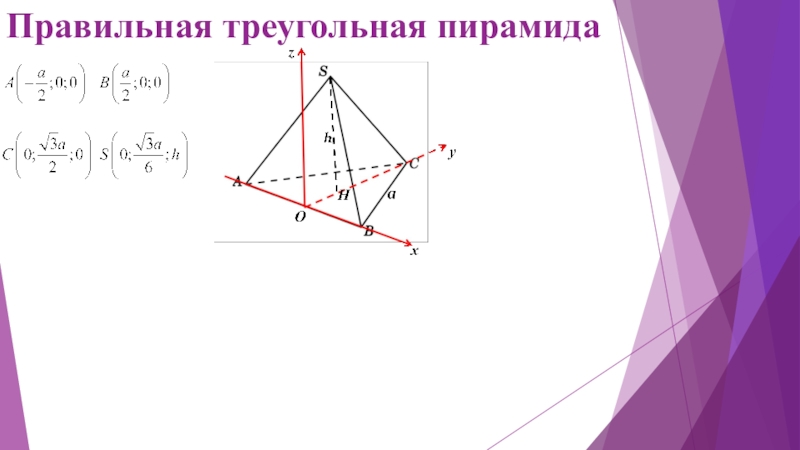
- 17. Правильная треугольная пирамида
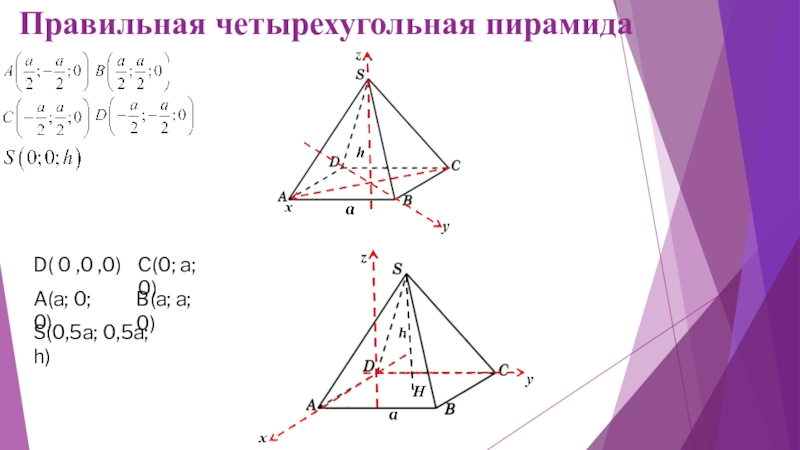
- 18. Правильная четырехугольная пирамидаD( 0 ,0 ,0) A(a; 0; 0)C(0; a; 0)B(a; a; 0)S(0,5a; 0,5a; h)
- 19. Правильная шестиугольная пирамида
- 20. Основные виды задачНахождение расстояния:Между прямой и плоскостьюМежду
- 21. Нахождение расстояния от точки до прямойРасстояние от
- 22. Нахождение расстояния между двумя точками, где M1 (x1; y1; z1), M2(x2; y2; z2)
- 23. Нахождение расстояния от точки М (x ;
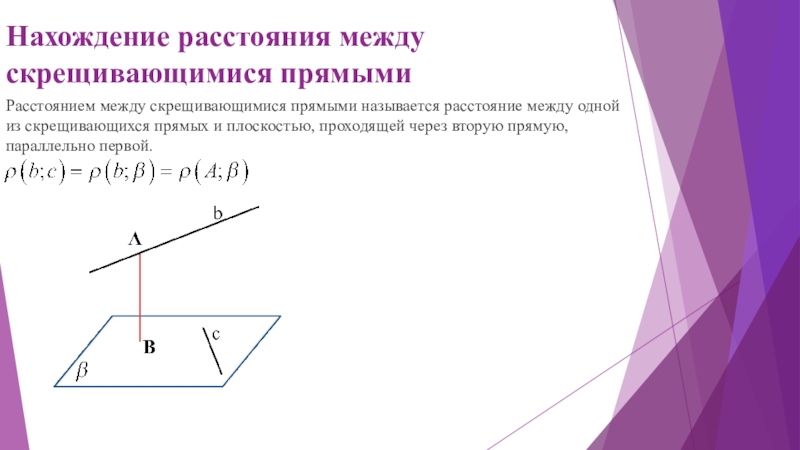
- 24. Нахождение расстояния между скрещивающимися прямымиРасстоянием между
- 25. Нахождение угла между прямымиУглом между скрещивающимися прямыми
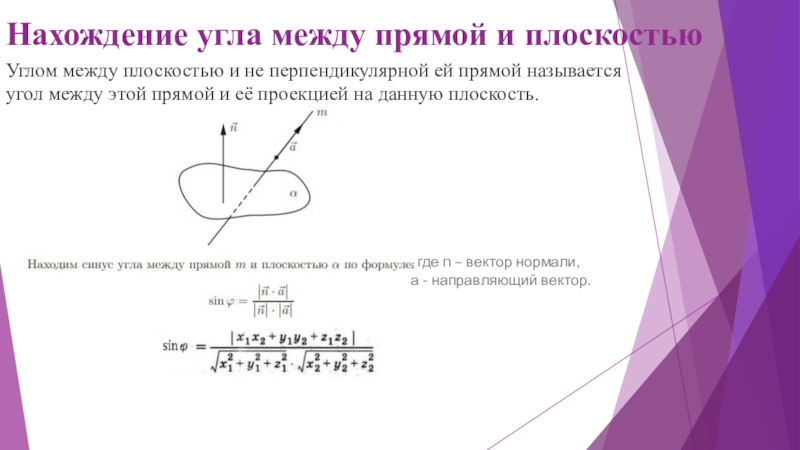
- 26. Нахождение угла между прямой и плоскостьюУглом между
- 27. Угол между плоскостями равен углу между векторами
- 28. Решение проблемы
- 29. Задача 4В правильной четырехугольной призме ABCDA1B1C1D1 со стороной
- 30. Вывод: Существует ряд стереометрических задач, для
- 31. Заключение: В ходе работы мною были
- 32. Используемая литература:1. Атанасян Л.С.и др. Геометрия, 10-11:
- 33. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1Автор:
Самохина Кристина,
ученица 11 Б класса
Руководитель: С.А. Максименко,
учитель математики
Координатный метод решения
Слайд 2Цель Определить виды стереометрических задач из ЕГЭ профильного уровня и методы
Задачи
Слайд 3Объект исследования: Стереометрические задачи.
Предмет исследования:
Методы решения стереометрических задач.
Слайд 4Планируемый результат: Определить наиболее рациональный метод решения стереометрических задач и научиться
Слайд 6Гипотеза: Координатный метод позволяет наиболее рационально и быстро решать геометрические задачи. Актуальность:
Слайд 7Алгебра - не что иное как записанная в символах геометрия, а геометрия -
Слайд 8Постановка проблемы
Решить задачу: В правильной четырехугольной призме АBCDA1B1C1D1 стороны основания
Методы решения:
- поэтапно-вычислительный;
- координатный метод.
Слайд 10Основные понятия
Метод координат — весьма эффективный и универсальный способ нахождения любых
Данный метод решения заключается во введении (привязке к исследуемым фигурам) декартовой системы координат, а затем – исчислении образующихся векторов (их длин и углов между ними). Достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций.
Прямоугольная (декартова) система координат в пространстве – совокупность точки О (называемой началом координат), единицы измерения и трёх попарно перпендикулярных прямых Ox, Oy и Oz (называемых осями координат: Ox – ось абсцисс, Oy – ось ординат, Oz – ось аппликат), на каждой из которых указано направление положительного отсчёта. Плоскости хОу, уОz и zOx называют координатными плоскостями. Каждой точке пространства ставится в соответствие тройка чисел, называемых её координатами.
Слайд 14Прямоугольный параллелепипед
D (0; 0; 0)
D1 (0; 0; c)
A (a; 0; 0)
A1
C (0; b; 0)
C1 (0; b; c)
B (a; b; 0)
B1 (a; b; c)
Слайд 18Правильная четырехугольная пирамида
D( 0 ,0 ,0)
A(a; 0; 0)
C(0; a; 0)
B(a;
S(0,5a; 0,5a; h)
Слайд 20Основные виды задач
Нахождение расстояния:
Между прямой и плоскостью
Между скрещивающимися прямыми
Между двумя точками
От
Нахождение угла:
Между скрещивающимися прямыми
Между прямой и плоскостью
Между плоскостями
Слайд 21Нахождение расстояния от точки до прямой
Расстояние от точки до прямой –
Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(x; y; z) до прямой можно найти, используя следующую формулу:
|Ax + By + Cz|
d=
√A + B + C
Слайд 23Нахождение расстояния от точки М (x ; y ; z) до
Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
Итак, для того, чтобы найти расстояние от точки до плоскости нам необходимо найти координаты точки, и координаты нормали данной плоскости. После чего воспользоваться следующей формулой:
Алгоритм решения задач на нахождение расстояния от точки до
плоскости:
1. На рисунке изображаем указанные в задаче прямые (которым придаем направление, т.е. вектора)
2. Вписываем фигуру в систему координат
3. Находим координаты точек (данной и трех точек плоскости)
4. Составляем уравнение плоскости
5. Находим координаты вектора нормали плоскости
6. Подставляем в формулу "расстояние от точки до плоскости"
Слайд 24
Нахождение расстояния между скрещивающимися прямыми
Расстоянием между скрещивающимися прямыми называется расстояние между
Слайд 25Нахождение угла между прямыми
Углом между скрещивающимися прямыми называется угол между двумя
Алгоритм решения задач на нахождение угла между скрещивающимися прямыми:
на рисунке изображаем указанные в задаче прямые (которым придаем направление, т.е. вектора)
вписываем фигуру в систему координат
находим координаты концов векторов
находим координаты векторов
подставляем в формулу "косинус угла между векторами"
находим значение самого угла
Слайд 26Нахождение угла между прямой и плоскостью
Углом между плоскостью и не перпендикулярной
, где n – вектор нормали,
а - направляющий вектор.
Слайд 27Угол между плоскостями равен углу между векторами нормалей к данным плоскостями
Вектор
Координаты вектора – это коэффициенты перед х, у, z в уравнении плоскости.
Формула для вычисления угла между плоскостями
Если заданы уравнения плоскостей A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу
Слайд 29Задача 4
В правильной четырехугольной призме ABCDA1B1C1D1 со стороной основания 12 и высотой
Задача 1
В кубе ABCDA1B1C1D1 точки E и F середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Задача 34
Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра.
Слайд 30Вывод: Существует ряд стереометрических задач, для которых более рациональным методом решения
Слайд 31Заключение: В ходе работы мною были изучены различные источники: книги, справочники,
Слайд 32Используемая литература:
1. Атанасян Л.С.и др. Геометрия, 10-11: учеб. для общеобразоват. учреждений:
2. Беликова И. Задание С2: Решаем методом координат // Математика, 2010, № 20.
3. Смирнов В.А. ЕГЭ-2011. Математика. Задача С2. Геометрия. Стереометрия / под ред. А.Л. Семенова, И.В. Ященко. —М.: МЦНМО, 2011.
4. Шабунин М.И. Математика для поступающих в вузы: пособие. —2-е изд., испр. и доп. —М.: БИНОМ, 2003.
5. https://4ege.ru/matematika/5137-reshenie-zadaniy-s2-ege-po-matematike-koordinatno-vektornym-metodom.html
6.https://www.metod-kopilka.ru/reshenie_zadaniy_s2_koordinatnym_metodom.-29500.htm
7. https://ege-study.ru/wp-content/uploads/pdf-materials/vectors.pdf
8. https://ege.sdamgia.ru/test?theme=283