- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Исследовательская работа по математике на тему Платоновы тела 10класс
Содержание
- 1. Исследовательская работа по математике на тему Платоновы тела 10класс
- 2. Ни одни геометрические тела не обладают
- 3. Цель исследования: расширить собственные знания о
- 4. Определение и виды многогранников
- 5. Их только 5!Составлен из шести квадратов. Каждая
- 6. Теорема Эйлера Для всякого выпуклого многогранника между
- 7. Платон (ок. 428 - ок. 348
- 8. Олицетворение многогранников
- 9. Феодария (Circjgjnia icosahtdra) Скелет одноклеточного организма
- 10. Многогранники вокруг нас Сальвадор Дали «Тайная вечеря»Икосаэдро-додекаэдроваяструктура
- 11. Создание моделей правильных многогранников с помощью развертококтаэдр додекаэдр тетраэдр икосаэдр куб
- 12. Создание моделей правильных многогранников с помощью оригами
- 13. Личностью человек становится только тогда, когда начинает
Слайд 1Платоновы тела
Научный руководитель
учитель математики
Шилова Любовь Юрьевна.
Выполнено
ученицей 10 класса
Козловой Дианой.
Слайд 2
Ни одни геометрические тела
не обладают
таким совершенством и красотой,
как
"Правильных многогранников вызывающе
мало, - написал когда-то Л.Кэрролл, -
но этот весьма скромный по численности
отряд сумел пробраться
в самые глубины различных наук".
Слайд 3
Цель исследования: расширить собственные знания о правильных многогранниках.
Задачи исследования:
1)
2)изучить свойства правильных многогранников и их развертках;
3)показать роль математических знаний в развитии общества, науки и искусства;
4)найти различные методы для создания моделей правильных многогранников;
5)изготовить модели правильных многогранников с помощью разверток и методами оригами.
Слайд 4
Определение и виды многогранников
Выпуклый многогранник называется правильным,
его грани являются правильными многоугольниками с одним и тем же числом сторон,
в каждой вершине многогранника сходится одно и тоже число граней,
все его двухгранные углы равны.
Виды правильных
многогранников
«эдра» - грань
«тетра» - четыре
«гекса» - шесть
«окта» - восемь
« додека» - двенадцать
«икоса» - двадцать
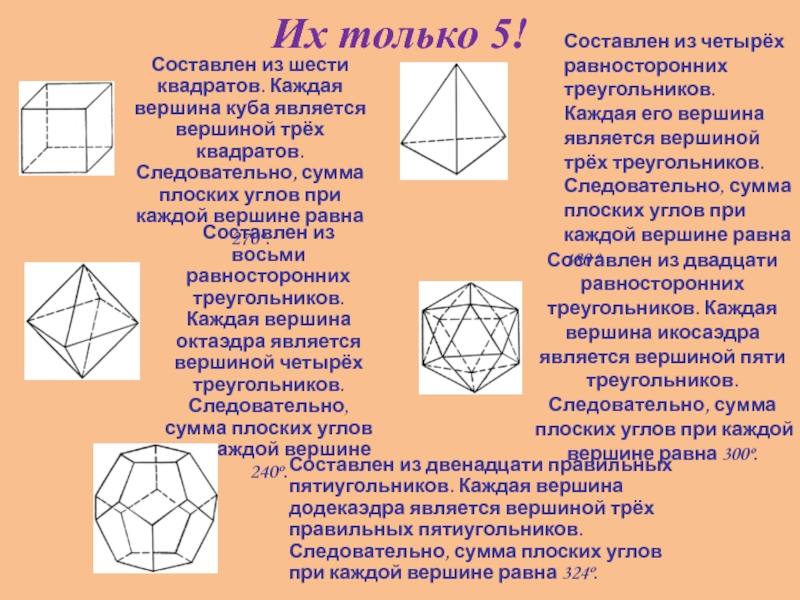
Слайд 5Их только 5!
Составлен из шести квадратов. Каждая вершина куба является вершиной
Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180 º.
Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Следовательно, сумма плоских углов при каждой вершине 240º.
Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300º.
Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324º.
Слайд 6Теорема Эйлера
Для всякого выпуклого многогранника
между числами В, Г и Р
соотношение
В+Г - Р = 2 ( вершины, грани, рёбра)
Эйлер Леонард (1707-1783)
Математик, механик, физик и астроном. По происхождению - швейцарец. Окончил Базельский университет (1724). Работал в России в 1727 - 1741 и в 1766 - 1783 годах. Адьюнкт (1726), а в 1731 - 1741 и с 1766 года - академик Петербургской Академии наук.
Слайд 7
Платон
(ок. 428 - ок. 348 до н.э.)
Правильные многогранники иногда называют Платоновыми
Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.
Слайд 9
Феодария
(Circjgjnia icosahtdra)
Скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме
Чем же вызвана такая природная геометризация феодарии?
По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Многогранники вокруг нас
Вирусы
Вирусы, построенные только из нуклеиновой кислоты и белка, могут походить на жесткую палочкообразную или гибкую нитевидную спираль, точнее на правильный двадцатигранник, или икосаэдр
Алюмокалиевые квасцы
Кристалл пирита
(сернистого колчедана )
В микромире в форме куба кристаллизуется поваренная соль, сернистый цинк и другие вещества
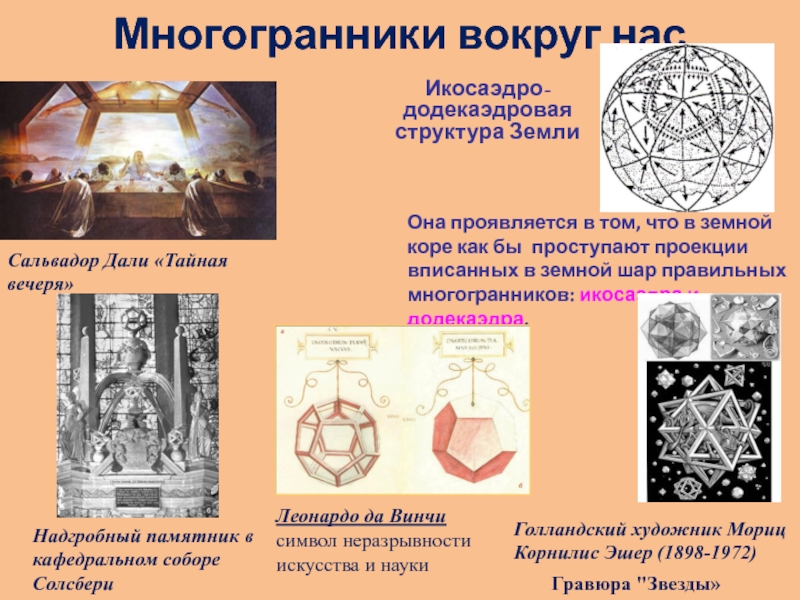
Слайд 10Многогранники вокруг нас
Сальвадор Дали «Тайная вечеря»
Икосаэдро-
додекаэдровая
структура Земли
Она проявляется в том, что
Надгробный памятник в кафедральном соборе Солсбери
Леонардо да Винчи
символ неразрывности искусства и науки
Голландский художник Мориц Корнилис Эшер (1898-1972)
Гравюра "Звезды»
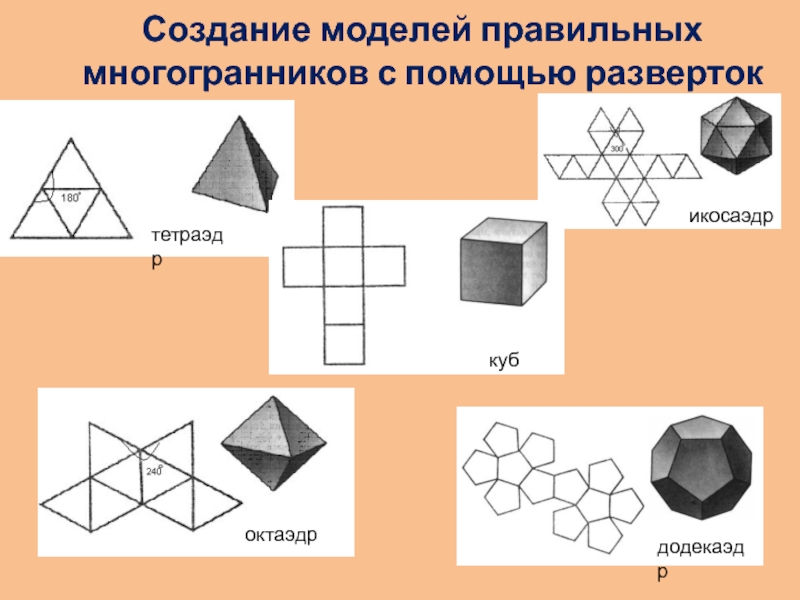
Слайд 11Создание моделей правильных многогранников с помощью разверток
октаэдр
додекаэдр
тетраэдр
икосаэдр
куб
Слайд 13Личностью человек становится только тогда, когда начинает самостоятельно выполнять творческую деятельность.
Итак, благодаря многогранникам, открываются не только свойства геометрических фигур, но и пути познания природы, науки, жизни.