- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Готовимся к зачету
Содержание
- 1. Готовимся к зачету
- 2. Готовимся к ЗАЧЕТУ( билет1)Дайте определение отрезка, луча,
- 3. 3. Докажите признак равенства треугольников по двум сторонам и углу между ними.
- 4. Докажите, что угол 1 равен углу 2.
- 5. Билет №2Дайте определение равных фигур. Определение середины
- 6. Дайте определение равных фигур. Определение середины отрезка и биссектрисы угла.
- 7. 2.Докажите признак равенства треугольников по стороне и двум прилежащим углам.
- 8. 3.Угол при основании равнобедренного треугольника равен 370
- 9. 4.На прямой отмечены точки A, B, C
- 10. Билет 3Дайте определение смежных углов. Сформулируйте свойство
- 11. Вопрос 2 Докажите признак равенства треугольников по
- 12. 3)один из углов, образованных при пересечении двух
- 13. Билет 41)Дайте определение вертикальных углов. Сформулируйте свойство
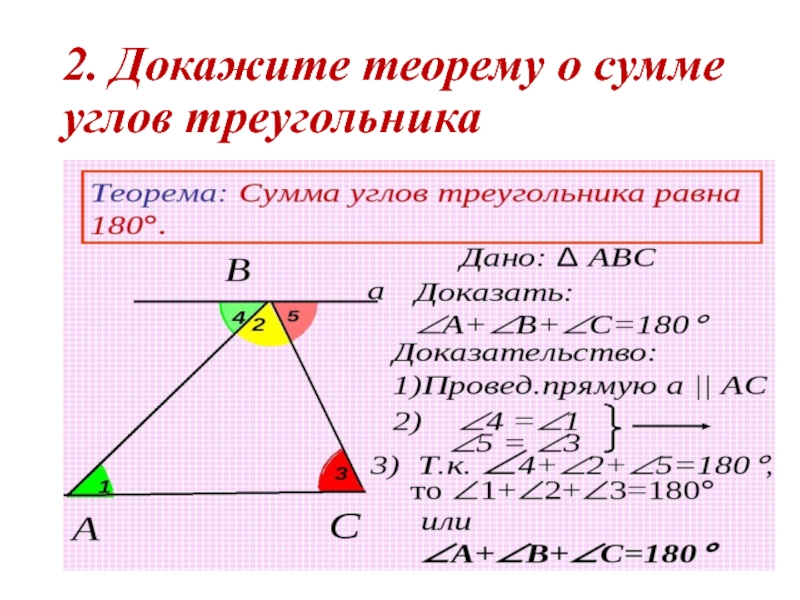
- 14. 2. Докажите теорему о сумме углов треугольника
- 15. 3) Доказать равенство треугольников ADM и AFE
- 16. 4) Один из внутренних односторонних углов, образованных
- 17. Билет 51) Дайте определение острого, прямого и тупого угла2) Докажите свойство биссектрисы равнобедренного треугольника
- 18. Докажите равенство треугольников COD и AOD.градусные меры
- 19. Т.к. градусные меры внешних углов Δ= 139°и
- 20. Билет №6 1. Дайте определение равнобедренного треугольника.
- 21. 1. Дайте определение равнобедренного треугольника. Сформулируйте свойства
- 22. Слайд 22
- 23. 3. Один из острых углов прямоугольного треугольника
- 24. 4. AC II DB, CO=OD. Доказать, что
- 25. БИЛЕТ№ 71. Дайте определение медианы, биссектрисы и
- 26. ВОПРОС 11. Дайте определение медианы, биссектрисы и
- 27. ВОПРОС 22. Сформулируйте признаки параллельных прямых. Доказать один по выбору.ТЕОРЕМА1:ТЕОРЕМА 2
- 28. Докажем признак №2Текст слайда
- 29. ТЕОРЕМА – третий признак параллельности прямых
- 30. Вопрос 3. Периметр равнобедренного треугольника 19 см,
- 31. Вопрос 44. В прямоугольном треугольнике острый угол
- 32. Билет 8Вопрос 1.ВОПРОС 2. Докажите, что при
- 33. Слайд 33
- 34. 3. Один из углов, образованных при пересечении двух прямых, на 500 меньше другого. Найти эти углы.
- 35. 4 . Найти углы треугольника ABC. МΔАМС
- 36. БИЛЕТ 9Дайте определение остроугольного, прямоугольного, тупоугольного
- 37. 2. Доказать, что при пересечении двух
- 38. 3. Один из острых углов прямоугольного
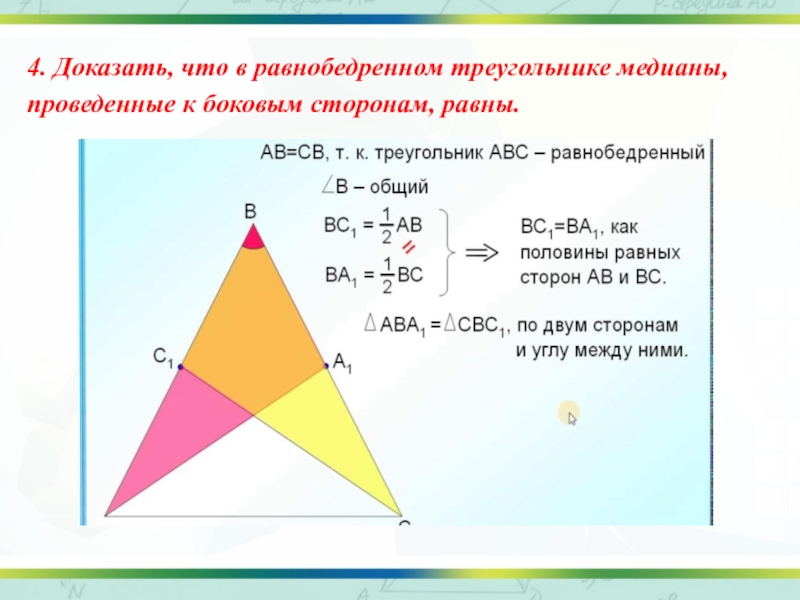
- 39. 4. Доказать, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
- 40. БИЛЕТ 101) Дайте определение параллельных прямых
- 41. Слайд 41
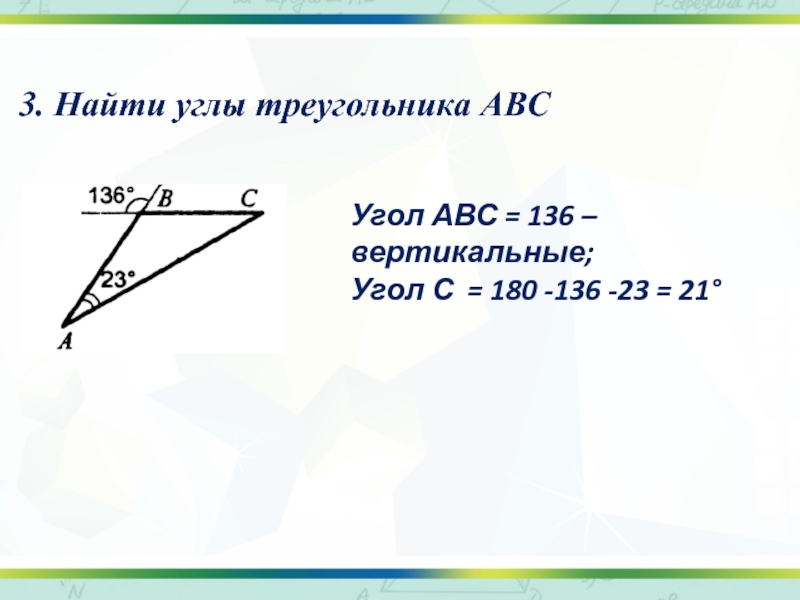
- 42. 3. Найти углы треугольника АВСУгол АВС
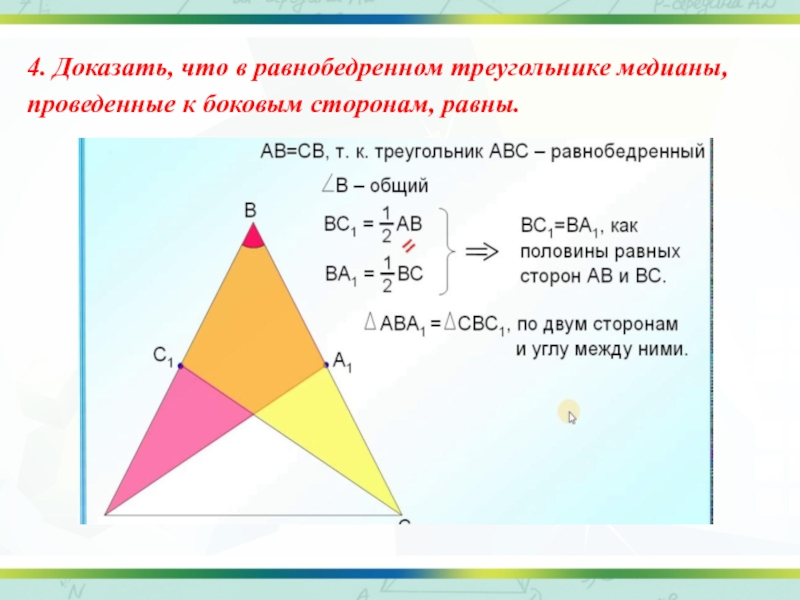
- 43. 4. Доказать, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
- 44. °Билет 111)Дайте определение окружности, центра, радиуса,
- 45. °2) . Докажите свойство углов при основании равнобедренного треугольника
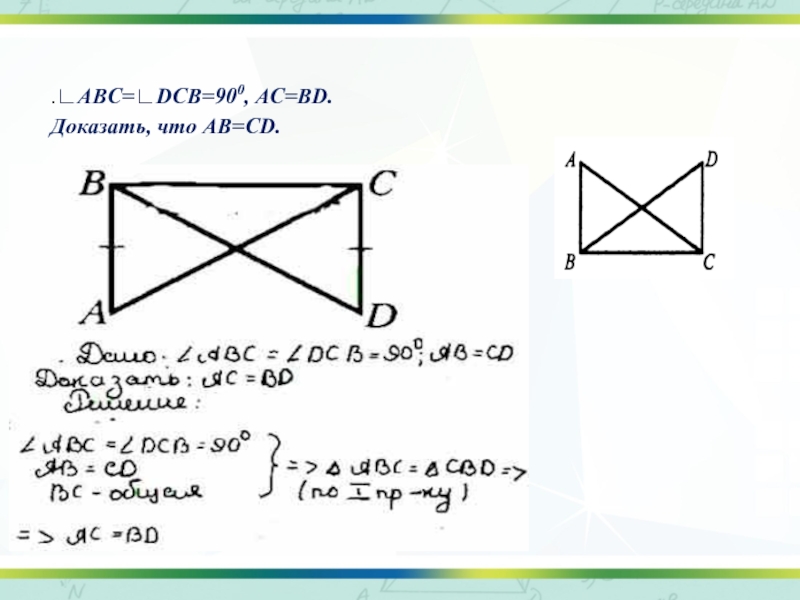
- 46. °.∟ABC=∟DCB=900, АС=BD. Доказать, что AB=CD.
- 47. 4)Высоты остроугольного треугольника NPT, проведенные из вершин
- 48. Билет 12 1) Дайте определение параллельных прямых
- 49. 2) Докажите теорему о соотношении между сторонами
- 50. Предположим, что это не так. Тогда возможны два
- 51. Следствие
- 52. .3) Внешний угол равнобедренного треугольника равен 640.
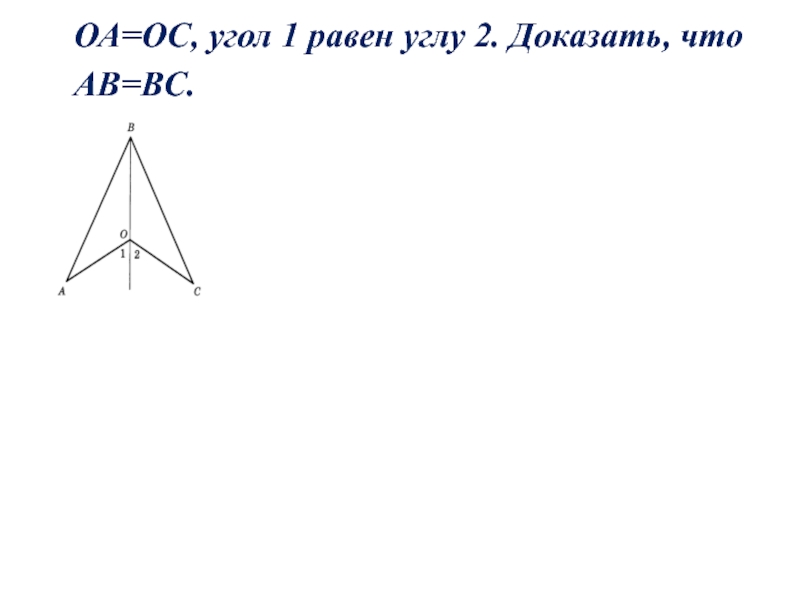
- 53. ОА=ОС, угол 1 равен углу 2. Доказать, что АВ=ВС.
- 54. Билет №13 1. Дайте определение расстояния от
- 55. 2. Докажите, что каждая сторона треугольника меньше
- 56. 3. Углы FDB и CBD равны, углы
- 57. 4. Доказать, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
- 58. Билет №141) Сформулируйте признаки равенства прямоугольных треугольников
- 59. 2)Докажите свойство внешнего угла треугольника.
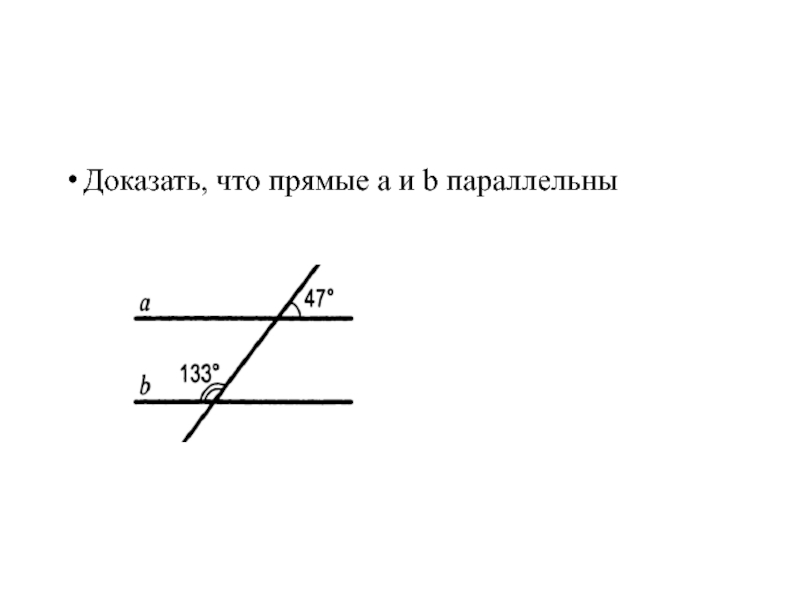
- 60. Доказать, что прямые a и b параллельны
- 61. 4) . В прямоугольном треугольнике KPE ∟P=900,
- 62. Билет 151). Дайте определение секущей? Назовите пары
- 63. 2)Докажите свойство катета прямоугольного треугольника, лежащего против угла в 300. Сформулировать обратное утверждение
- 64. Луч BD проходит между сторонами угла ABC
- 65. 4.В треугольнике АВС (АВ=ВС) на сторонах АВ
Готовимся к ЗАЧЕТУ( билет1)Дайте определение отрезка, луча, угла. Определение развернутого угла. Обозначение лучей и углов. В прямоугольном треугольнике DEF катет DF=12 см., ∟E=300 . Найдите гипотенузу DE.
Слайд 2Готовимся к ЗАЧЕТУ( билет1)
Дайте определение отрезка, луча, угла. Определение развернутого угла.
Обозначение лучей и углов.
В прямоугольном треугольнике DEF катет DF=12 см., ∟E=300 . Найдите гипотенузу DE.
В прямоугольном треугольнике DEF катет DF=12 см., ∟E=300 . Найдите гипотенузу DE.
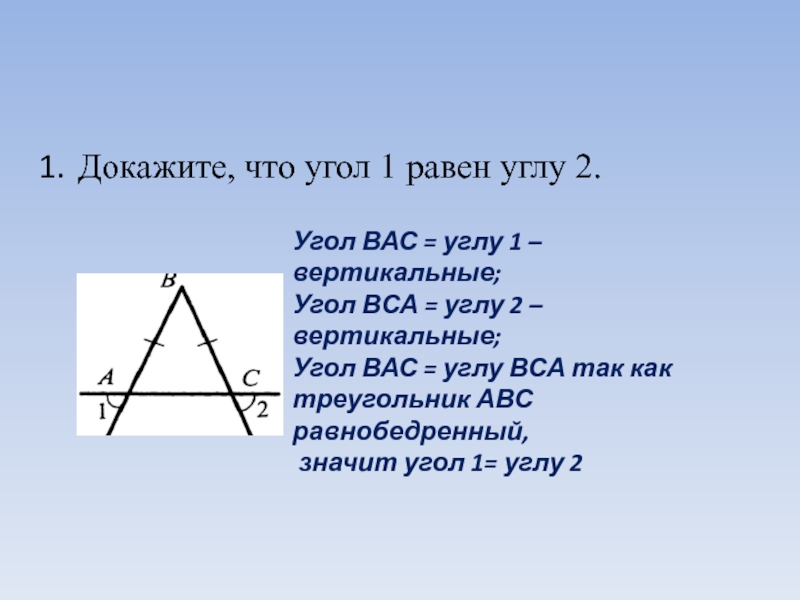
Слайд 4Докажите, что угол 1 равен углу 2.
Угол ВАС = углу
1 – вертикальные;
Угол ВСА = углу 2 – вертикальные;
Угол ВАС = углу ВСА так как
треугольник АВС равнобедренный,
значит угол 1= углу 2
Угол ВСА = углу 2 – вертикальные;
Угол ВАС = углу ВСА так как
треугольник АВС равнобедренный,
значит угол 1= углу 2
Слайд 5Билет №2
Дайте определение равных фигур. Определение середины отрезка и биссектрисы угла.
Докажите
признак равенства треугольников по стороне и двум прилежащим углам.
Угол при основании равнобедренного треугольника равен 370 . Найдите угол при вершине.
На прямой отмечены точки A, B, C и D , AB=8 см., BD=6 см., BC=3 см. Найдите AD.
Угол при основании равнобедренного треугольника равен 370 . Найдите угол при вершине.
На прямой отмечены точки A, B, C и D , AB=8 см., BD=6 см., BC=3 см. Найдите AD.
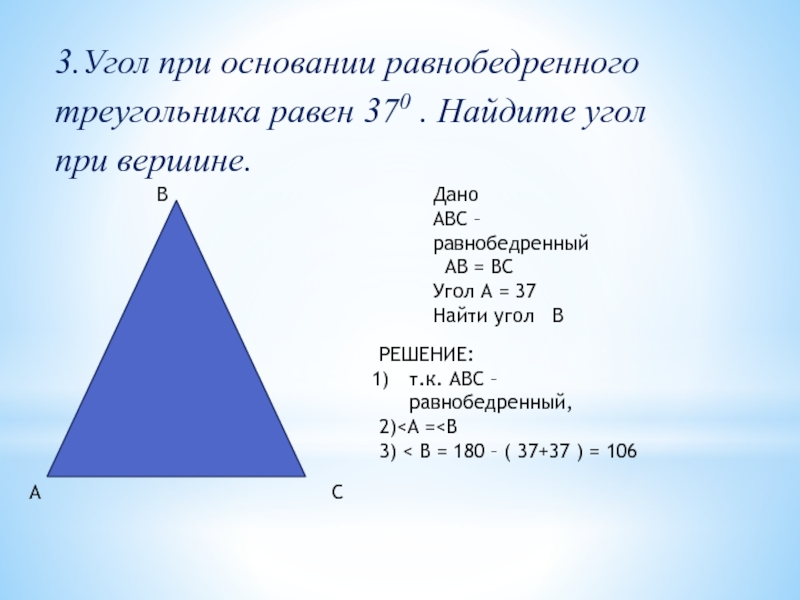
Слайд 83.Угол при основании равнобедренного треугольника равен 370 . Найдите угол при
вершине.
А
В
С
Дано
АВС – равнобедренный
АВ = ВС
Угол А = 37
Найти угол В
РЕШЕНИЕ:
т.к. АВС – равнобедренный,
2)<А =<В
3) < В = 180 – ( 37+37 ) = 106
Слайд 94.На прямой отмечены точки A, B, C и D , AB=8
см., BD=6 см., BC=3 см. Найдите AD.
А
В
С
Д
АД = 8+6 = 14
Слайд 10Билет 3
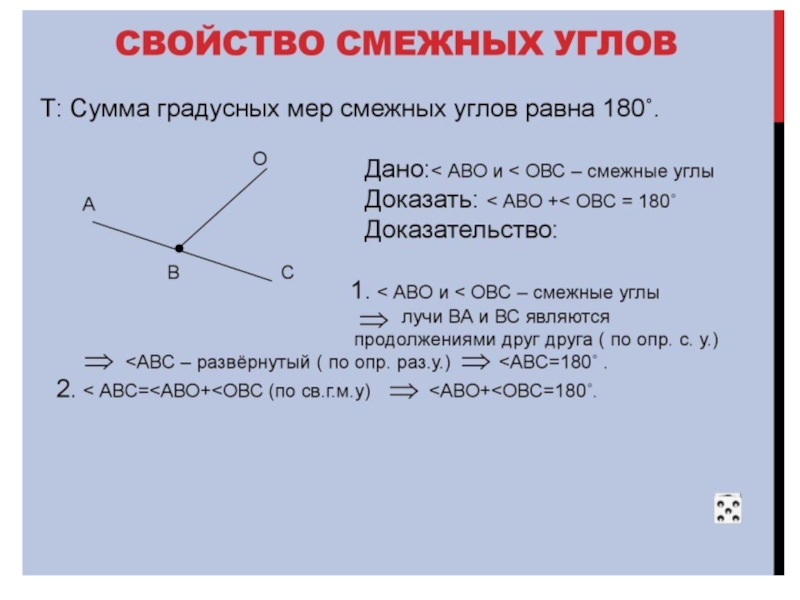
Дайте определение смежных углов. Сформулируйте свойство смежных углов.
.Смежные углы —
это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой. Сумма смежных углов равна 180º
.
.
Слайд 11Вопрос 2 Докажите признак равенства треугольников по трем сторонам.
Если три стороны
одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Слайд 123)один из углов, образованных при пересечении двух прямых, равен 700. Найти
остальные три угла.
70; 110
4)В треугольнике ABC ∟A=800 , ∟B=400. Биссектриса угла A пересекает сторону BC в точке F. Найдите угол ACF.
(Как мы помним, биссектриса делит угол пополам, соответственно углы BAF и FАС будут равны 40 градусам. Рассмотрим треугольник BAF: Угол В равен 40 градусов и угол А равен 40 градусов, найдём угол F: 180 - (40 + 40) = 100 градусов. Теперь рассмотрим треугольник FАС: Углы ВFА и АFС смежные, находим угол АFС: 180 - 100 = 80. Теперь из треугольника FАС находим угол С: 180 - (80 + 40) = 60 градусов. Этот же угол и АСF.
70; 110
4)В треугольнике ABC ∟A=800 , ∟B=400. Биссектриса угла A пересекает сторону BC в точке F. Найдите угол ACF.
(Как мы помним, биссектриса делит угол пополам, соответственно углы BAF и FАС будут равны 40 градусам. Рассмотрим треугольник BAF: Угол В равен 40 градусов и угол А равен 40 градусов, найдём угол F: 180 - (40 + 40) = 100 градусов. Теперь рассмотрим треугольник FАС: Углы ВFА и АFС смежные, находим угол АFС: 180 - 100 = 80. Теперь из треугольника FАС находим угол С: 180 - (80 + 40) = 60 градусов. Этот же угол и АСF.
Слайд 13Билет 4
1)Дайте определение вертикальных углов. Сформулируйте свойство вертикальных углов
Вертикальные углы —
это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
Вертикальные углы равны. При пересечении двух прямых образуются две пары вертикальных углов
Вертикальные углы равны. При пересечении двух прямых образуются две пары вертикальных углов
Слайд 164) Один из внутренних односторонних углов, образованных при пересечении двух параллельных
прямых третьей, в 3 раза больше другого. Чему равны эти углы?
Пусть меньший из углов равен х, тогда другой равен 3х Значит
3х + х = 4х = 180°, следовательно, х = 45°. Ответ: 45° и 135°
Слайд 17Билет 5
1) Дайте определение острого, прямого и тупого угла
2) Докажите свойство
биссектрисы равнобедренного треугольника
Слайд 18Докажите равенство треугольников COD и AOD.
градусные меры двух внешних углов треугольника
равны 1390 и 870. Найдите третий внешний угол треугольника
Слайд 19Т.к. градусные меры внешних углов Δ= 139°и 87°. то смежные с
ними внутренние углы Δ будут 180°-139°=41° и 180°-87°=93°
сумма углов в любом Δ=180° ⇒ третий угол в Δ=180°-41°-93°=46°
тогда смежный внешний угол будет 180°-46°=134°
Слайд 20Билет №6
1. Дайте определение равнобедренного треугольника. Сформулируйте свойства равнобедренного треугольника.
2.
Докажите свойства смежных и вертикальных углов.
3. Один из острых углов прямоугольного треугольника 370. Найти второй острый угол.
4. AC II DB, CO=OD. Доказать, что треугольники СОА и DOB равны.
3. Один из острых углов прямоугольного треугольника 370. Найти второй острый угол.
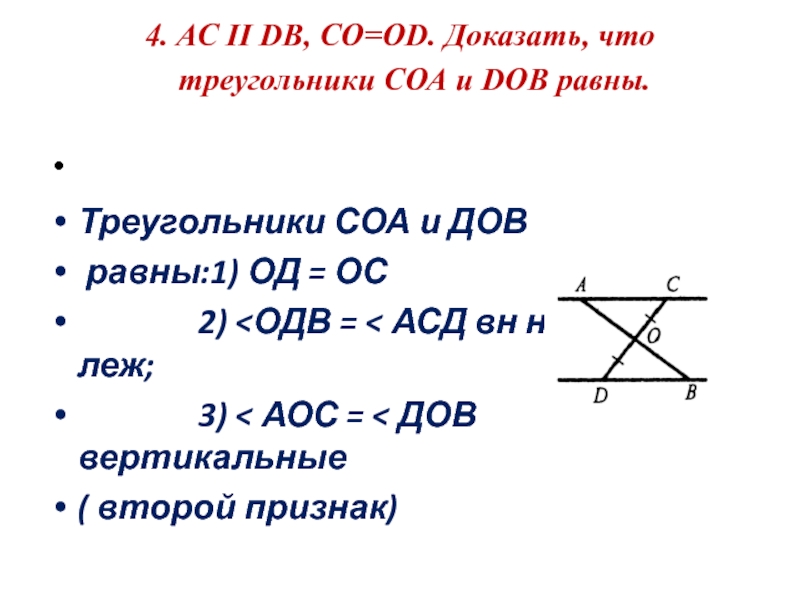
4. AC II DB, CO=OD. Доказать, что треугольники СОА и DOB равны.
Слайд 211. Дайте определение равнобедренного треугольника. Сформулируйте свойства равнобедренного треугольника.
Равнобедренный треугольник -
треугольник, у которого две стороны равны. Эти равные стороны называются боковыми, а третья - основание. В равнобедренном треугольнике: Боковые стороны равны; Углы при основании равны Высота, опущенная к основанию, является также и биссектрисой и медианой этого
Слайд 233. Один из острых углов прямоугольного треугольника 370. Найти второй острый
угол.
Два угла в прямоугольном треугольнике 90 градусов, значит второй угол 90-37 =53
Ответ 53 градуса
Два угла в прямоугольном треугольнике 90 градусов, значит второй угол 90-37 =53
Ответ 53 градуса
Слайд 244. AC II DB, CO=OD. Доказать, что треугольники СОА и DOB
равны.
Треугольники СОА и ДОВ
равны:1) ОД = ОС
2) <ОДВ = < АСД вн накрест леж;
3) < АОС = < ДОВ вертикальные
( второй признак)
Слайд 25БИЛЕТ№ 7
1. Дайте определение медианы, биссектрисы и высоты треугольника.
2. Сформулируйте
признаки параллельных прямых. Доказать один по выбору.
3. Периметр равнобедренного треугольника 19 см, а основание – 7 см. Найти боковую сторону треугольника.
4. В прямоугольном треугольнике острый угол равен 600 , а биссектриса этого угла – 8 см. Найдите длину катета, лежащего против этого угла.
3. Периметр равнобедренного треугольника 19 см, а основание – 7 см. Найти боковую сторону треугольника.
4. В прямоугольном треугольнике острый угол равен 600 , а биссектриса этого угла – 8 см. Найдите длину катета, лежащего против этого угла.
Слайд 26ВОПРОС 1
1. Дайте определение медианы, биссектрисы и высоты треугольника
Медиана треугольника –
это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника - это отрезок биссектрисы угла треугольника( Луч делящий угол треугольника пополам).
Высота треугольника – это перпендикуляр, опущенный из вершины угла треугольника на противоположную сторону треугольника.
Биссектриса треугольника - это отрезок биссектрисы угла треугольника( Луч делящий угол треугольника пополам).
Высота треугольника – это перпендикуляр, опущенный из вершины угла треугольника на противоположную сторону треугольника.
Слайд 27ВОПРОС 2
2. Сформулируйте признаки параллельных прямых. Доказать один по выбору.
ТЕОРЕМА1:
ТЕОРЕМА 2
Слайд 30Вопрос 3
. Периметр равнобедренного треугольника 19 см, а основание – 7
см. Найти боковую сторону треугольника.
Треугольник равнобедренный, то две его стороны равны
Значит, Боковая сторона = (19 - 7):2= 12:2=6.
Ответ: 6 см.
Слайд 31Вопрос 4
4. В прямоугольном треугольнике острый угол равен 600 , а
биссектриса этого угла – 8 см. Найдите длину катета, лежащего против этого угла.
А
С
В
ДАНО:
< А = 60°, АК = 8см
Найти :
ВС
Решение:
Δ АСК прямоуг, КС против 30 градусов, равна
Половине АК; КС = 4см
Δ ВАК равнобедренный, ВК = АК = 8 см;
ВС = 12 см
К
Слайд 32Билет 8
Вопрос 1
.
ВОПРОС 2. Докажите, что при пересечении двух параллельных прямых
секущей накрест лежащие углы равны.
.
1. Дайте определение внешнего угла треугольника. Сформулируйте свойство внешнего угла треугольника.
Внешним углом треугольника называется угол, смежный с каким – нибудь углом треугольника
Внешний угол треугольника равен сумме острых углов не смежных с ним
Слайд 343. Один из углов, образованных при пересечении двух прямых, на 500
меньше другого. Найти эти углы.
Слайд 35
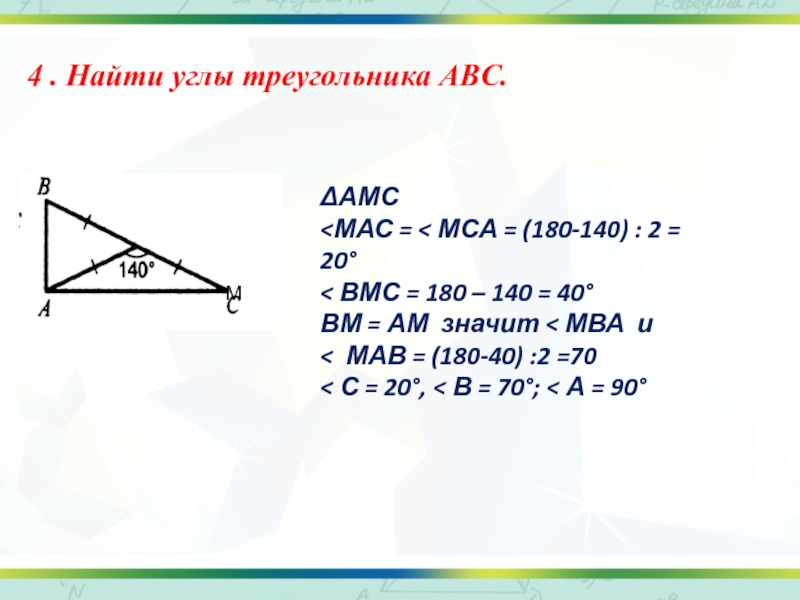
4 . Найти углы треугольника ABC.
М
ΔАМС
(180-140) : 2 = 20°
< ВМС = 180 – 140 = 40°
ВМ = АМ значит < МВА и
< МАВ = (180-40) :2 =70
< С = 20°, < В = 70°; < А = 90°
< ВМС = 180 – 140 = 40°
ВМ = АМ значит < МВА и
< МАВ = (180-40) :2 =70
< С = 20°, < В = 70°; < А = 90°
Слайд 36
БИЛЕТ 9
Дайте определение остроугольного, прямоугольного, тупоугольного треугольника.
Треугольник у которого
все углы острые – остроугольный;
Если есть прямой угол – треугольник прямоугольный;
Если есть тупой угол – треугольник тупоугольный
Если есть прямой угол – треугольник прямоугольный;
Если есть тупой угол – треугольник тупоугольный
Слайд 37
2. Доказать, что при пересечении двух параллельных прямых секущей а)
соответственные углы равны, б) сумма односторонних равна 180 0.
Слайд 38
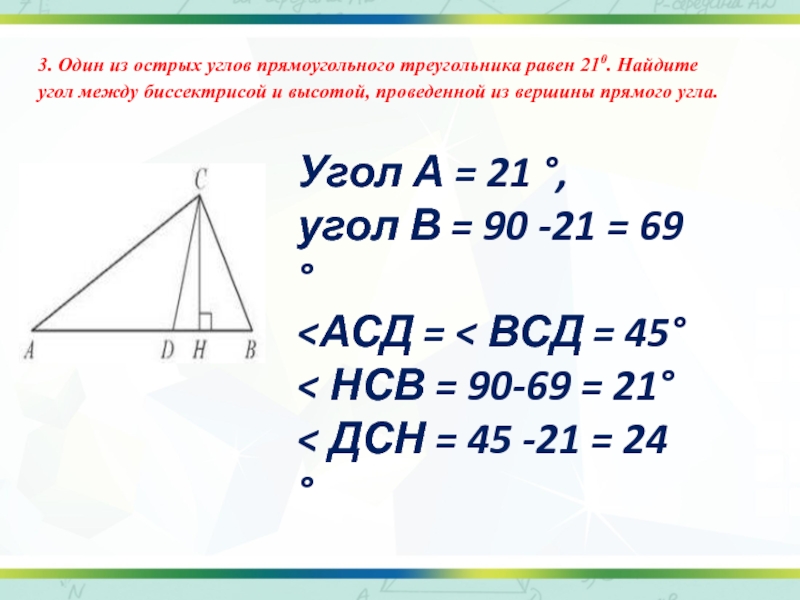
3. Один из острых углов прямоугольного треугольника равен 210. Найдите
угол между биссектрисой и высотой, проведенной из вершины прямого угла.
Угол А = 21 °,
угол В = 90 -21 = 69 °
<АСД = < ВСД = 45°
< НСВ = 90-69 = 21°
< ДСН = 45 -21 = 24 °
Слайд 39
4. Доказать, что в равнобедренном треугольнике медианы, проведенные к боковым
сторонам, равны.
Слайд 40
БИЛЕТ 10
1) Дайте определение параллельных прямых и параллельных отрезков
)Две прямые
называются параллельными , если они не пересекаются.
Два отрезка называются параллельными, если они лежат на параллельных прямых.
2)Докажите теорему о соотношении между сторонами и углами треугольника
( прямую или обратную).
Слайд 43
4. Доказать, что в равнобедренном треугольнике медианы, проведенные к боковым
сторонам, равны.
Слайд 44
°
Билет 11
1)Дайте определение окружности, центра, радиуса, хорды, диаметра и дуги
окружности
Окружность - это замкнутая кривая линия, все точки которой находятся на равном расстоянии от данной точки плоскости, называемой центром окружности. Круг - это часть плоскости, ограниченная окружностью. Расстояние от любой точки круга до центра круга не превышает расстояния от центра круга до любой точки на окружности. Радиус - отрезок прямой линии, соединяющий центр с любой точкой окружности. Диаметр – отрезок прямой линии, соединяющии две точки окружности и проходящий через центр. Можно так - это наибольшая из хорд окружности. Дуга - часть окружности или другой кривой линии, заключенная между двумя точками. Хорда - прямая, соединяющая две точки кривой линии.
Окружность - это замкнутая кривая линия, все точки которой находятся на равном расстоянии от данной точки плоскости, называемой центром окружности. Круг - это часть плоскости, ограниченная окружностью. Расстояние от любой точки круга до центра круга не превышает расстояния от центра круга до любой точки на окружности. Радиус - отрезок прямой линии, соединяющий центр с любой точкой окружности. Диаметр – отрезок прямой линии, соединяющии две точки окружности и проходящий через центр. Можно так - это наибольшая из хорд окружности. Дуга - часть окружности или другой кривой линии, заключенная между двумя точками. Хорда - прямая, соединяющая две точки кривой линии.
Слайд 474)Высоты остроугольного треугольника NPT, проведенные из вершин N и P, пересекаются
в точке K, ∟T = 560. Найдите угол NKP.
Пусть высота из N будет NM, высота из Р – РН
Высоты треугольника пересекаются в одной точке.
В прямоугольных ∆ РНТ и ∆ РКМ угол НРТ - общий.
Сумма острых углов треугольника 90°.
Поэтому ∠РКМ=∠РТN=56°
Искомый угол NKPсмежный углу РКМ. В сумме они составляют развёрнутый угол=180°.
Угол NKP=180°-56°=124°
Слайд 48Билет 12 1) Дайте определение параллельных прямых и параллельных отрезков. Сформулируйте аксиому
параллельных прямых.
Параллельные прямые — это две непересекающиеся прямые, лежащие в одной плоскости. Параллельные прямые записываются через знак параллельности «||».
Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Если при пересечении двух прямых секущей:
накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180°, то прямые параллельны
Если две параллельные прямые пересечены секущей, то:
накрест лежащие углы равны; соответственные углы равны; сумма односторонних углов равна 180°.
Слайд 492) Докажите теорему о соотношении между сторонами и углами треугольника (
прямую или обратную). Следствия из теоремы
Отложим на стороне АВ отрезок АD, равный стороне АС.
АD АВ, т.к. по построению АD = АС, а по условию АС АВ, значит, точка D лежит между точками А и В. Следовательно, 1 является частью С, т.е. С 1. Угол 2 внешний угол DBC, поэтому 2 В. АDС - равнобедренный с основанием DC, т.к. по построению АD = АС, следовательно, 1 = 2 (углы при основании).
Итак, С 1, 1 = 2, значит, С 2, при этом 2 В, следовательно, С В.
Слайд 50Предположим, что это не так. Тогда возможны два варианта:
либо АВ = АС, тогда АВС - равнобедренный с основанием ВС,
значит, С = В (как углы при основании), что противоречит условию: С В.
либо АВ АС, тогда С В, т.к. против большей стороны лежит больший угол (смотри 1 часть доказательства), что противоречит условию: С В.
Значит, наше предположение неверно, следовательно, АВ АС. Что и требовалось доказать.
либо АВ АС, тогда С В, т.к. против большей стороны лежит больший угол (смотри 1 часть доказательства), что противоречит условию: С В.
Значит, наше предположение неверно, следовательно, АВ АС. Что и требовалось доказать.
Слайд 52.3) Внешний угол равнобедренного треугольника равен 640. Найдите углы треугольника.
если внешний
угол при вершине равен 64 градуса.
1)180-64=116(один угол)
2)180-116=64(сумма двух углов)
3)64:2=32
Ответ: Два угла равны 32 градусов и один равен 116градуса.
Слайд 54Билет №13
1. Дайте определение расстояния от точки до прямой. Наклонная. Определение
расстояния между параллельными прямыми.
Расстояние от точки до прямой — это длина перпендикуляра, опущенного из данной точки на данную прямую. Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой. Поэтому, чтобы найти расстояние между параллельными прямыми, надо: 1) выбрать на одной из параллельных прямых точку; 2) опустить из выбранной точки к другой прямой перпендикуляр; 3) найти длину этого перпендикуляра.
Расстояние от точки до прямой — это длина перпендикуляра, опущенного из данной точки на данную прямую. Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой. Поэтому, чтобы найти расстояние между параллельными прямыми, надо: 1) выбрать на одной из параллельных прямых точку; 2) опустить из выбранной точки к другой прямой перпендикуляр; 3) найти длину этого перпендикуляра.
Слайд 552. Докажите, что каждая сторона треугольника меньше суммы двух других. Что
такое неравенство треугольника.
сумма углов треугольника равно 180 градусов. а если бы каждая сторона треугольника была бы больше суммы двух других сторон, то сумма углов была бы больше 180, что невозможно. следовательно - каждая сторона треугольника меньше суммы двух других сторон
сумма углов треугольника равно 180 градусов. а если бы каждая сторона треугольника была бы больше суммы двух других сторон, то сумма углов была бы больше 180, что невозможно. следовательно - каждая сторона треугольника меньше суммы двух других сторон
Слайд 563. Углы FDB и CBD равны, углы FBD и CDB равны.
Доказать, что равны углы F и C.
решение:
I. Рассмотрим треугольник CBD и треугольник FDB.
BD – общая
Угол FDB = углу CBD(по условию)
Угол FBD = углу CDB(по условию), следовательно треугольник CBD = треугольнику FDB(II признак равенства), следовательно угол F = углу C(соответственные элементы), ЧТД.
Слайд 574. Доказать, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам,
равны.
Слайд 614) . В прямоугольном треугольнике KPE ∟P=900, ∟K=600. На катете PE
отметили точку M такую, что ∟KMP=600. Найдите PM , если EM = 16 см.
Рассмотрим треугольник КМР:
∟ РКМ=90- ∟ КМР=90-60=30
2. ∟ РКЕ= ∟ РКМ+ ∟ МКЕ ∟ МКЕ= ∟ РКЕ- ∟ МКЕ=90-30=60= ∟ РКМ,значит КМ-биссектриса угла РКЕ
3. ∟ КЕР=90- ∟ РКЕ=90-60=30
∟ МКЕ= ∟ КЕМ, значит треугольник КЕМ-равнобедренный, отсюда КМ=МЕ=16 4.Рассмотрим треугольник КМР. т.к. в прямоугольном треугольнике катет, лежащий против угла в 30 градусов равен половине гипотенузы, то РМ=1/2КМ РМ=1/2*16=8
Ответ:8см
Рассмотрим треугольник КМР:
∟ РКМ=90- ∟ КМР=90-60=30
2. ∟ РКЕ= ∟ РКМ+ ∟ МКЕ ∟ МКЕ= ∟ РКЕ- ∟ МКЕ=90-30=60= ∟ РКМ,значит КМ-биссектриса угла РКЕ
3. ∟ КЕР=90- ∟ РКЕ=90-60=30
∟ МКЕ= ∟ КЕМ, значит треугольник КЕМ-равнобедренный, отсюда КМ=МЕ=16 4.Рассмотрим треугольник КМР. т.к. в прямоугольном треугольнике катет, лежащий против угла в 30 градусов равен половине гипотенузы, то РМ=1/2КМ РМ=1/2*16=8
Ответ:8см
Слайд 62Билет 15
1). Дайте определение секущей? Назовите пары углов, которые образуются при
пересечении двух прямых секущей.
Секущая - прямая по отношению к двум прямым, которая пересекает их в двух точках. При пересечении двух прямых секущей образуются накрест лежащие, односторонние и соответственные углы. Каждых видов углов по 4 пары.
Секущая - прямая по отношению к двум прямым, которая пересекает их в двух точках. При пересечении двух прямых секущей образуются накрест лежащие, односторонние и соответственные углы. Каждых видов углов по 4 пары.
Слайд 632)Докажите свойство катета прямоугольного треугольника, лежащего против угла в 300. Сформулировать
обратное утверждение
Слайд 64Луч BD проходит между сторонами угла ABC . Найдите угол DBC,
если ∟ABC = 630, ∟ABD = 510.
дано: угол ABC, луч BD проходит между сторон ABC, угол ABC = 63 градус, угол ABD = 51 градус. Найти градусную меру угла DBC — ? Решение: Рассмотрим угол АВС. Угол АВС состоит из углов АВD и DВС, то есть угол АВС = угол АВD + угол DВС. Тогда угол DВС = угол АВС - угол АВD; угол DВС = 63 градусов - 51 градус; угол DВС = 12 градусов. Ответ: угол DВС = 12 градусов.
дано: угол ABC, луч BD проходит между сторон ABC, угол ABC = 63 градус, угол ABD = 51 градус. Найти градусную меру угла DBC — ? Решение: Рассмотрим угол АВС. Угол АВС состоит из углов АВD и DВС, то есть угол АВС = угол АВD + угол DВС. Тогда угол DВС = угол АВС - угол АВD; угол DВС = 63 градусов - 51 градус; угол DВС = 12 градусов. Ответ: угол DВС = 12 градусов.
Слайд 654.В треугольнике АВС (АВ=ВС) на сторонах АВ и ВС отложены равные
отрезки АМ и СN соответственно. Докажите, что AN=СМ.
Угол М равен углу N и угол А равен углу С точка пересечения будет О пусть угол AOM равен углу CON Следует что AN=CM
Угол М равен углу N и угол А равен углу С точка пересечения будет О пусть угол AOM равен углу CON Следует что AN=CM
