- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Гл. 4 Урок 5. Вписанный и центральный углы
Содержание
- 1. Гл. 4 Урок 5. Вписанный и центральный углы
- 2. ●ОАBCD Если АВ - диаметр , то
- 3. Угол с вершиной в центре окружности называется
- 4. ●ОАBCили∠АВС=½ ·∠АОС Угол называется вписанным, если его
- 5. ●ОАBCили∠АВС=½ ·∠АОС Дано: Окр(О;r) ; ∠АВС-вписанный; ∠АОС-центральный.
- 6. ●ОАBCДано: Окр(О;r) ; ∠АВС-вписанный; ∠АОС-центральный. Доказать:
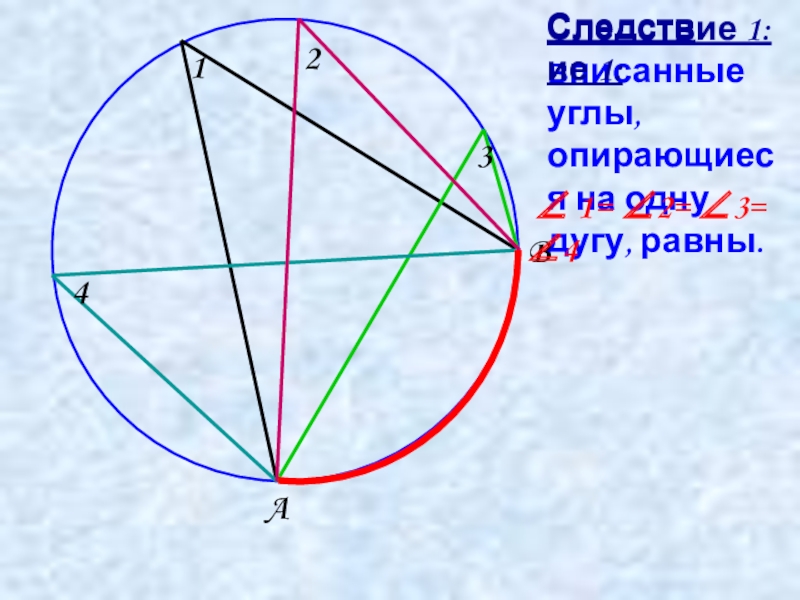
- 7. Следствие 1: вписанные углы, опирающиеся на одну дугу, равны.AB ∠ 1= ∠2= ∠3= ∠41324Следствие 1:
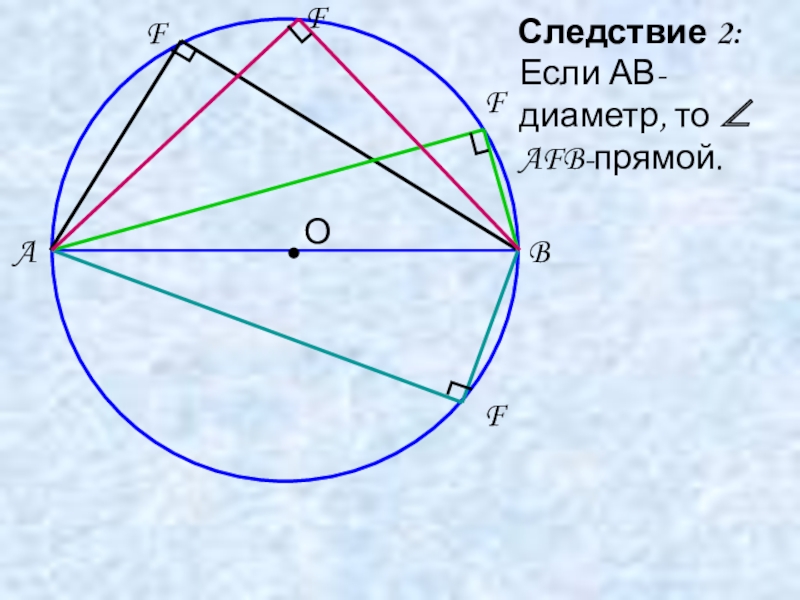
- 8. Следствие 2:ABЕсли АВ-диаметр, то ∠ AFB-прямой.FFFF┐┐┐┐•О
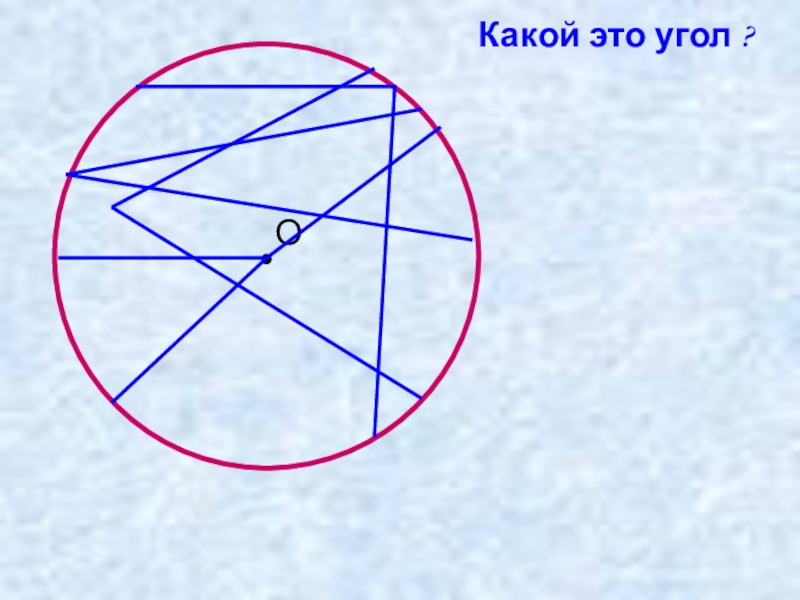
- 9. •ОКакой это угол ?
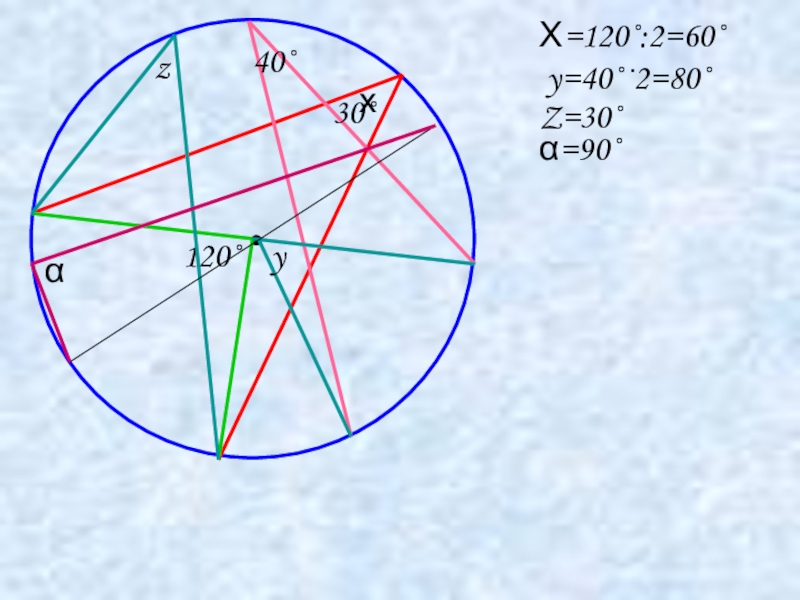
- 10. •х120˚Х=120˚:2=60˚40˚yy=40˚·2=80˚30˚zZ=30˚αα=90˚
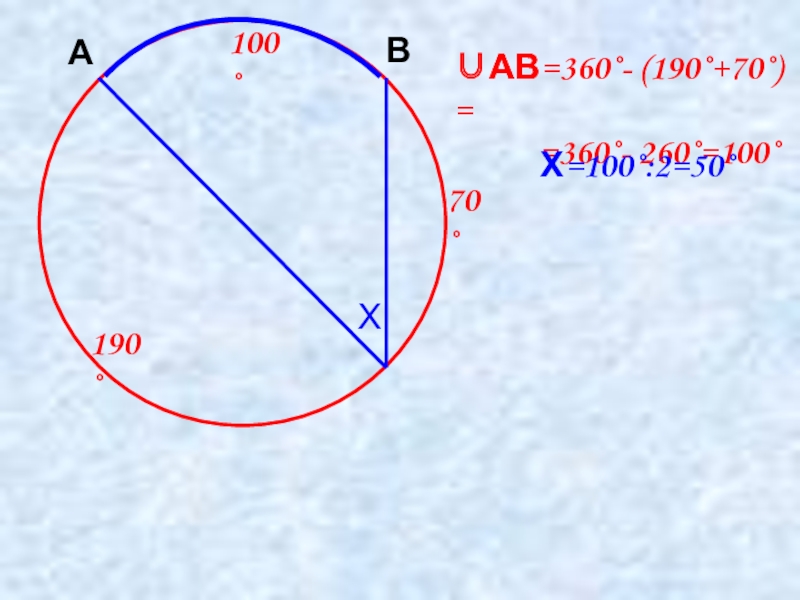
- 11. 190˚Х70˚АВ∪АВ=360˚- (190˚+70˚) = =360˚- 260˚=100˚100˚Х=100˚:2=50˚∪АВ=
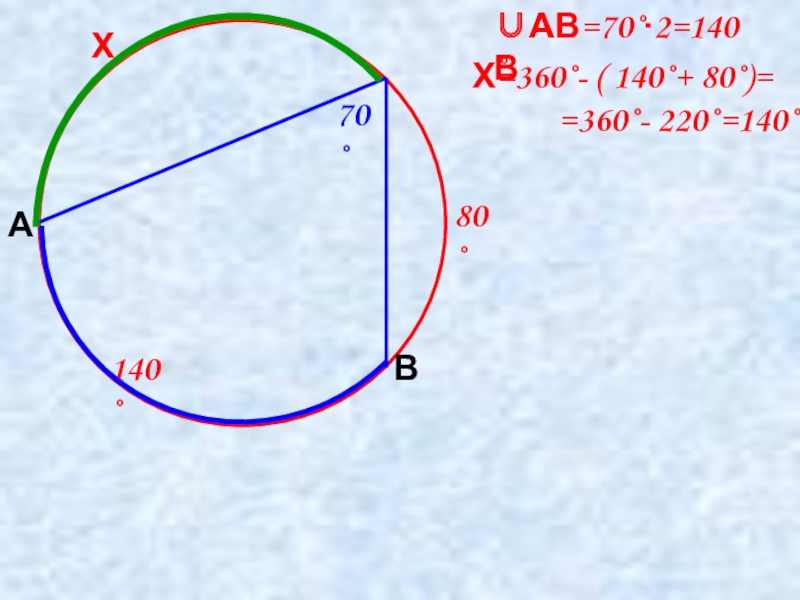
- 12. 80˚Х70˚АВХ=360˚- ( 140˚+ 80˚)= =360˚- 220˚=140˚∪АВ=70˚∙2=140˚∪АВ140˚
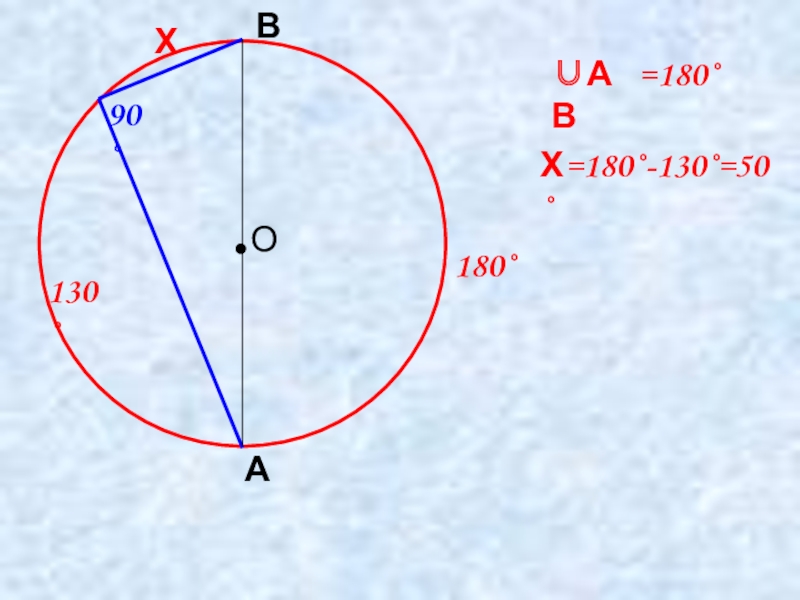
- 13. ОХАВ=180˚130˚Х=180˚-130˚=50˚•∪АВ180˚90˚
●ОАBCD Если АВ - диаметр , то АСВ – полуокружность,АДВ – полуокружность. Дуга-это часть окружности, заключённая между двумя точками.∪ АСB , ∪АДВ - дуги∪АВ - дуга●●
Слайд 2
●
О
А
B
C
D
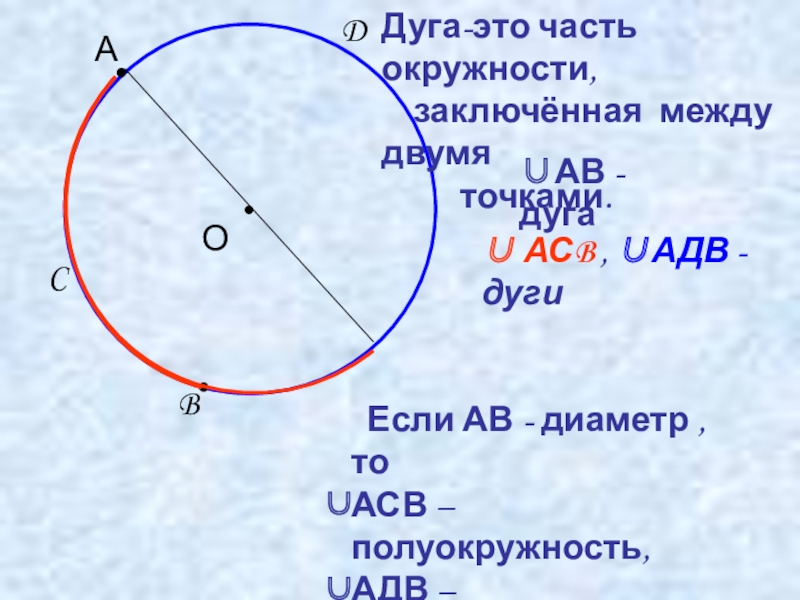
Если АВ - диаметр , то
АСВ – полуокружность,
АДВ –
полуокружность.
Дуга-это часть окружности,
заключённая между двумя
точками.
∪ АСB , ∪АДВ - дуги
∪АВ - дуга
●
●
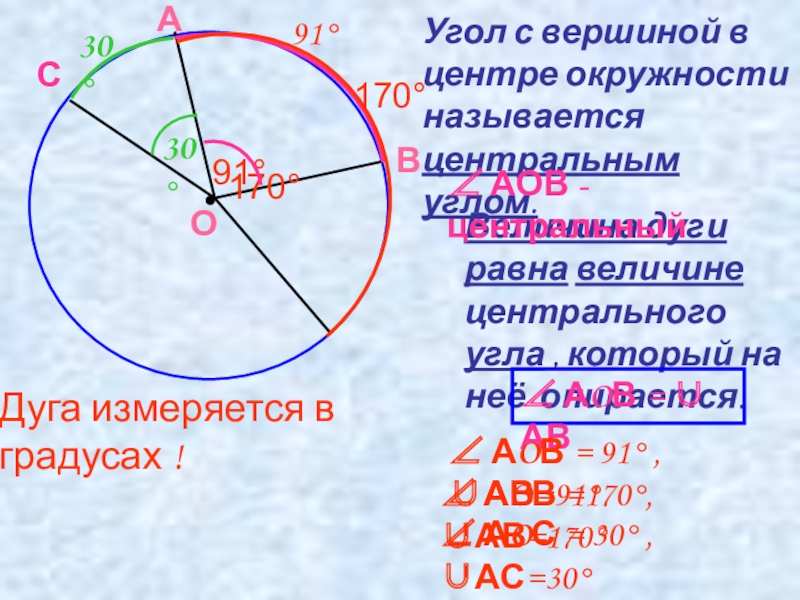
Слайд 3Угол с вершиной в центре окружности называется центральным углом.
О
А
В
170°
170°
Величина дуги
равна величине центрального угла , который на неё опирается.
∠ АОВ - центральный
Дуга измеряется в градусах !
91°
∠ АOВ = ∪ АВ
●
91°
∠ АOВ = 91° ,∪АВ=91°
∠ АOВ =170°,∪АВ=170°
∠ АOС = 30° ,∪АС=30°
С
30 °
30°
Слайд 4
●
О
А
B
C
или
∠АВС=½ ·∠АОС
Угол называется вписанным, если его вершина лежит на окружности,
а стороны пересекают окружность.
∠АBС-вписанный
∠АВС=½· ∪ АС
Вписанный угол измеряется половиной дуги, на которую он опирается.
Слайд 5
●
О
А
B
C
или
∠АВС=½ ·∠АОС
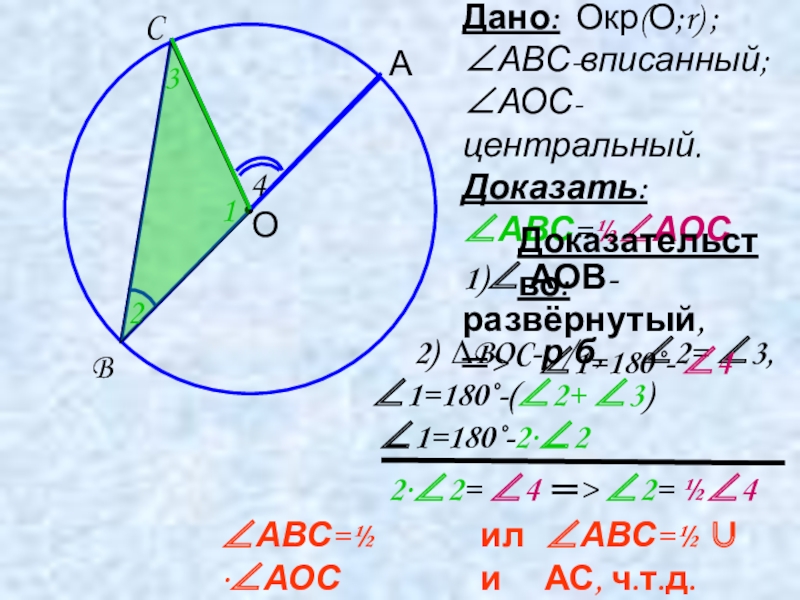
Дано: Окр(О;r) ; ∠АВС-вписанный; ∠АОС-центральный. Доказать: ∠АВС=½∠АОС
Доказательство:
∠АВС=½ ∪ АС, ч.т.д.
2) ∆BOC-р/б, ∠2= ∠3, ∠1=180˚-(∠2+ ∠3)
∠1=180˚-2·∠2
1
2
3
4
1)∠ АОВ-развёрнутый, ═> ∠1=180˚- ∠4
2·∠2= ∠4 ═> ∠2= ½∠4
Слайд 6
●
О
А
B
C
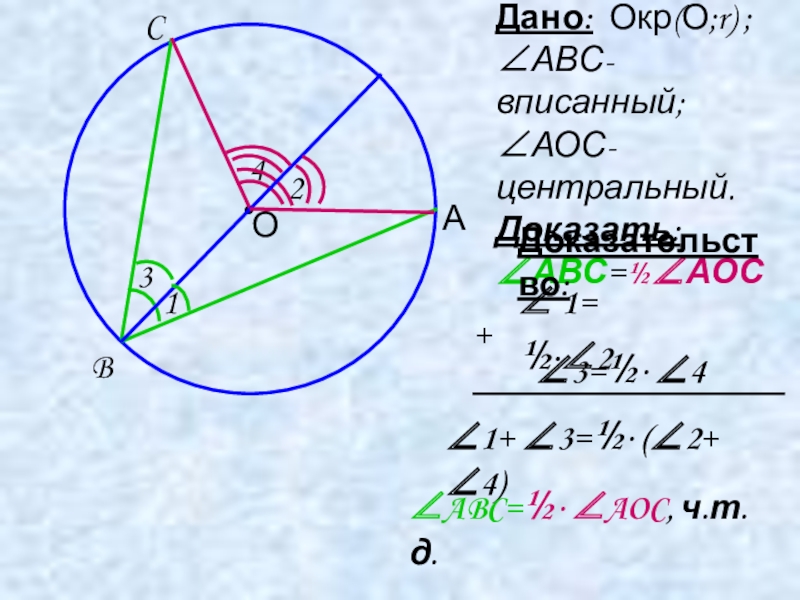
Дано: Окр(О;r) ; ∠АВС-вписанный; ∠АОС-центральный. Доказать: ∠АВС=½∠АОС
Доказательство:
1
2
3
4
∠ 1=
½·∠2
∠3=½· ∠4
∠1+ ∠3=½· (∠2+ ∠4)
∠ABC=½· ∠AOC, ч.т.д.
+
Слайд 7
Следствие 1: вписанные углы, опирающиеся на одну дугу, равны.
A
B
∠ 1=
∠2= ∠3= ∠4
1
3
2
4
Следствие 1:
