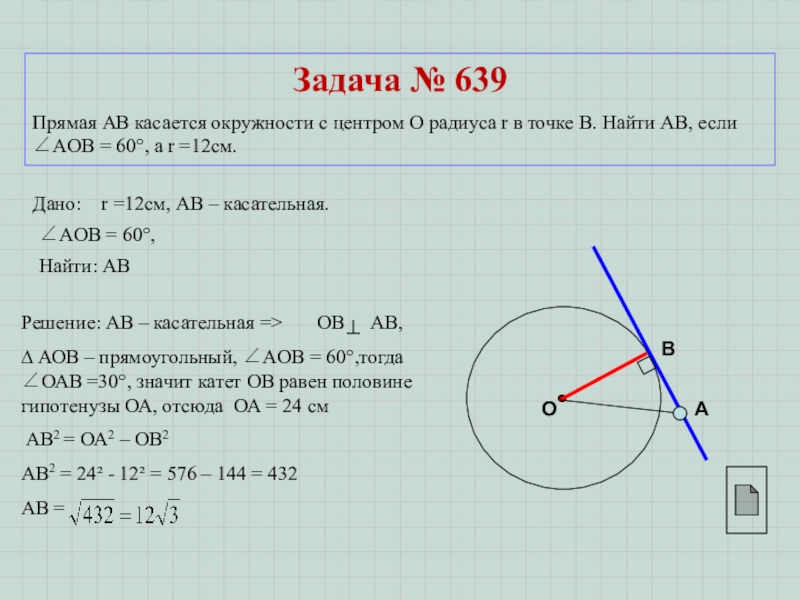
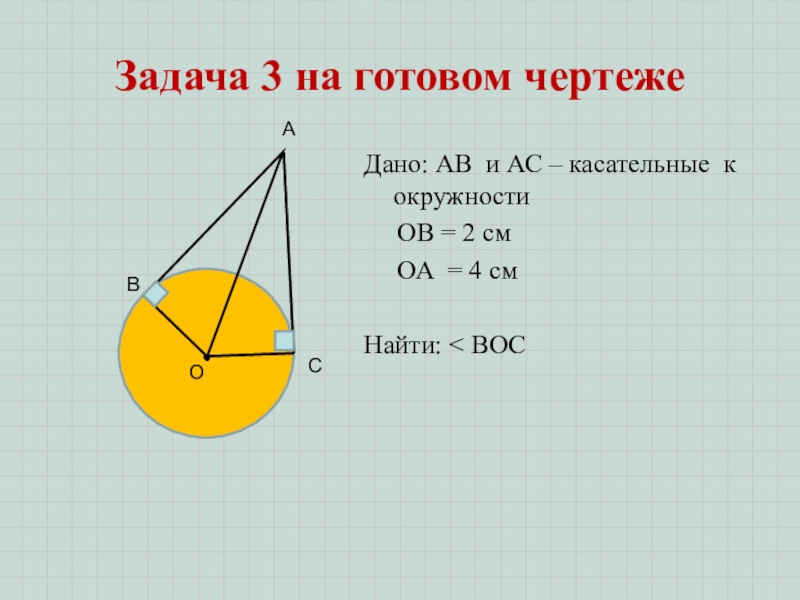
Дано: r =12см, АВ – касательная.
Решение: АВ – касательная => ОВ АВ,
∆ АОВ – прямоугольный, ∠АOВ = 60°,тогда ∠ОАВ =30°, значит катет ОВ равен половине гипотенузы ОА, отсюда ОА = 24 см
АВ2 = ОА2 – ОВ2
АВ2 = 24² - 12² = 576 – 144 = 432
АВ =
А
В
О
∠АOВ = 60°,
Найти: АВ
Доказательство:
Предположим, что это не так. То есть ОА будет наклонной. Но любая наклонная, проведенная из той же точки, что и перпендикуляр, будет больше перпендикуляра. ОН < ОА, то ОН < r. => d < r Значит, прямая р и окружность имеют две общие точки, что неверно => р ОА.
Теорема
(свойство касательной)
А
Дано: окружность (О; r);
луч р, перпендикуляр ОА.
Доказать: р – касательная.
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Обратная теорема
(признак касательной)
р
Доказательство: 1 = 2 = 900 ;
∆ АВО = ∆ АСО (ОА – общая; ОВ = ОС = r).
АВ = АС и 3 = 4.
О
А
B
С
2
4
3
1
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Свойство отрезков касательных, проведенных из одной точки
О
А
p
А
О
В
B
О
A
C
B
О
A
C
Является ли прямая АН касательной к окружности с радиусом 3 см?
б). ОА = 4 см
< НАО = 45°
в). ОА = 6 см
< НАО =30°
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Email: Нажмите что бы посмотреть
