треугольнике?
Каким свойством обладает средняя линия треугольника?
Какие треугольники называются равновеликими?
Сформулируйте свойство средней линии треугольника применительно к его площади;
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Гл. 3. Урок 10. Свойство медиан треугольника
Содержание
- 1. Гл. 3. Урок 10. Свойство медиан треугольника
- 2. Точка пересечения медиан треугольникаУчебная презентация по геометрии для 8 класса
- 3. Отрезки – элементы треугольника Медиана треугольника
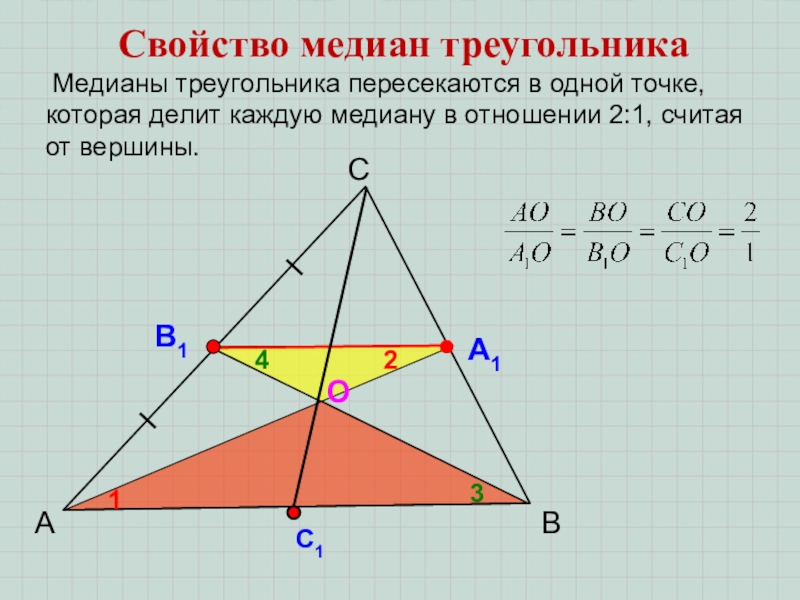
- 4. АСВСвойство медиан треугольника Медианы треугольника пересекаются в
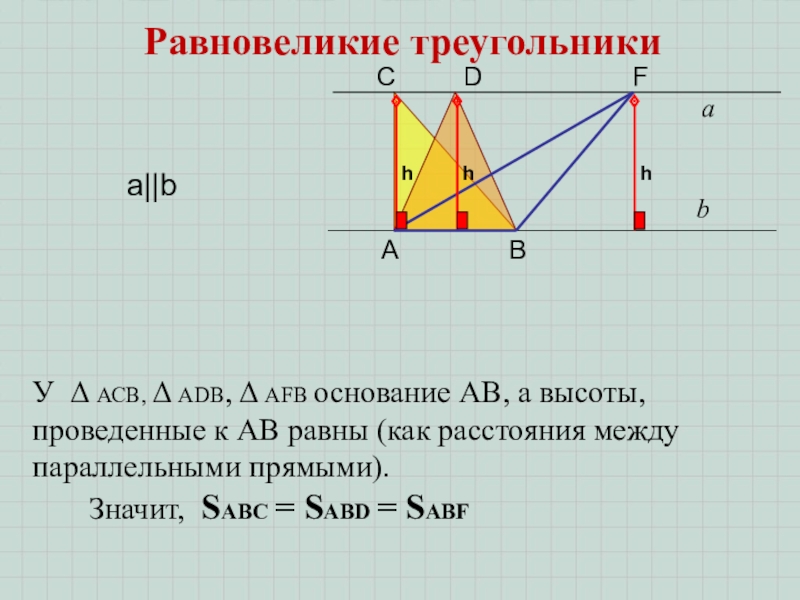
- 5. аbABCDFЗначит, SABC = SABD = SABFУ Δ
- 6. Медиана треугольника делит его на два равновеликих треугольника Следствие 1
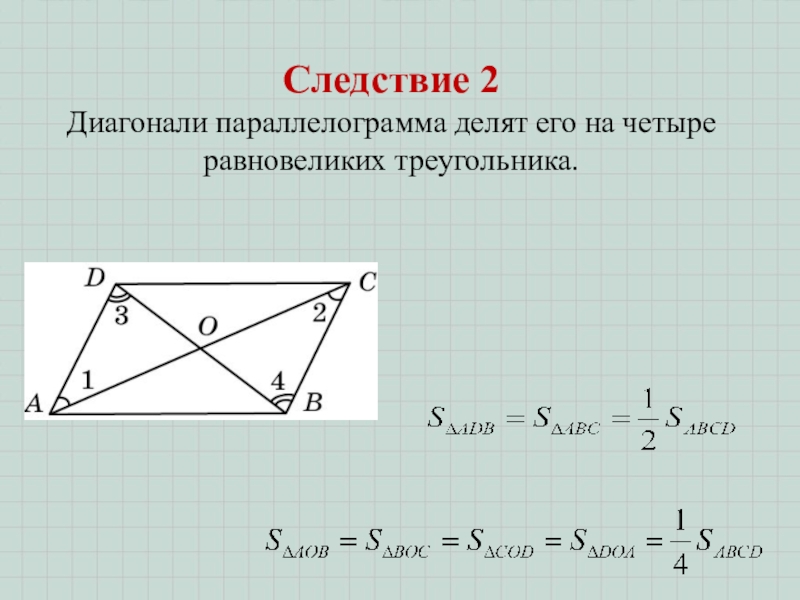
- 7. Следствие 2 Диагонали параллелограмма делят его на четыре равновеликих треугольника.
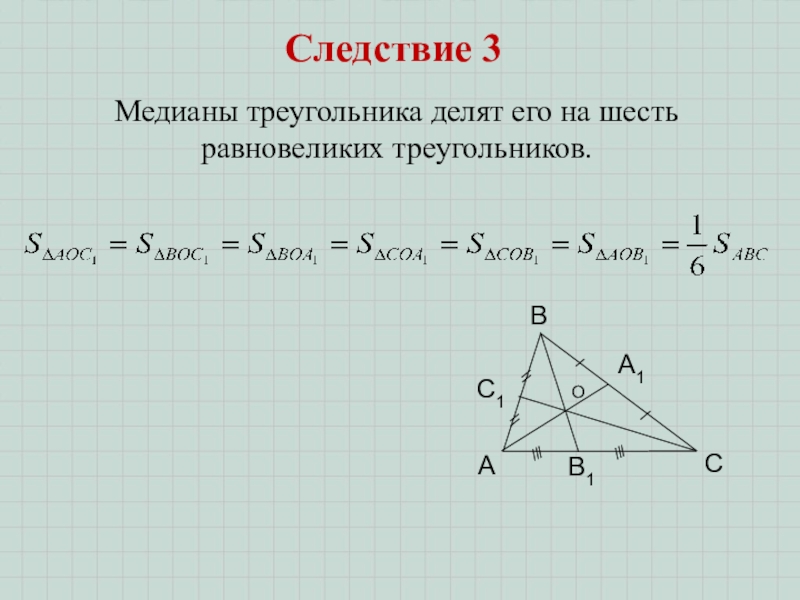
- 8. ВМедианы треугольника делят его на шесть равновеликих треугольников. Следствие 3
- 9. Решить задачу по готовому рисунку
- 10. Домашнее заданиеЧитать учебник П. 64 и записи
- 11. Выводы по урокуКакой отрезок называется медианой треугольника?Сколько
Точка пересечения медиан треугольникаУчебная презентация по геометрии для 8 класса
Слайд 1Повторение
Какой отрезок называется средней линией треугольника?
Сколько средних линий можно провести в
Слайд 3Отрезки – элементы треугольника
Медиана треугольника – отрезок, соединяющий вершину
треугольника с серединой противоположной стороны (рис. 1)
Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой противоположной стороны (рис. 2).
Высота треугольника – отрезок, соединяющий вершину треугольника с точкой противоположной стороны или ее продолжения и перпендикулярный этой стороне (рис. 3)
Слайд 4
А
С
В
Свойство медиан треугольника
Медианы треугольника пересекаются в одной точке, которая
делит каждую медиану в отношении 2:1, считая от вершины.
С1
Слайд 5
а
b
A
B
C
D
F
Значит, SABC = SABD = SABF
У Δ АСВ, Δ АDB, Δ
AFB основание АВ, а высоты, проведенные к АВ равны (как расстояния между параллельными прямыми).
Равновеликие треугольники
а||b
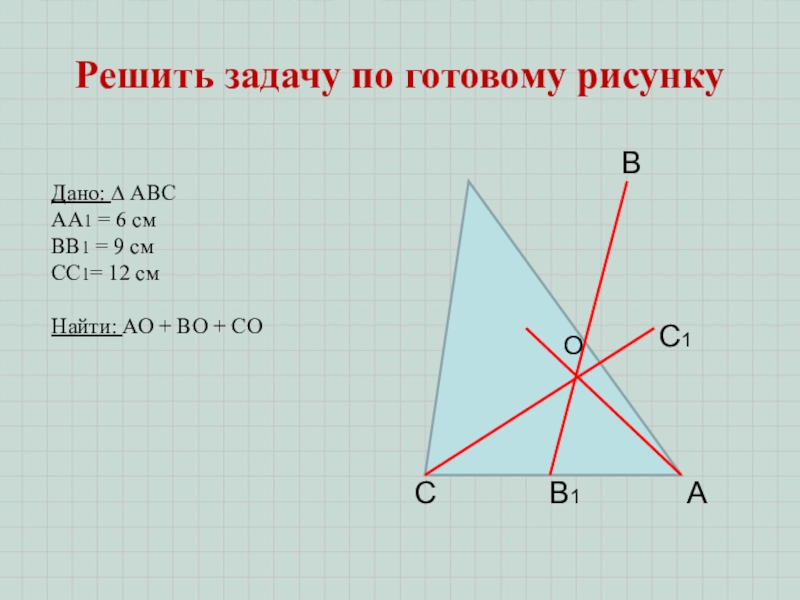
Слайд 9Решить задачу по готовому рисунку
В
А1
С1
С В1 А
А1
С1
С В1 А
О
Дано: ∆ АВС
АА1 = 6 см
ВВ1 = 9 см
СС1= 12 см
Найти: АО + ВО + СО
Слайд 10Домашнее задание
Читать учебник П. 64 и записи в тетради;
Отвечать на вопрос
9 на стр. 159;
Решить № 570, 571
Решить № 570, 571
Слайд 11Выводы по уроку
Какой отрезок называется медианой треугольника?
Сколько медиан можно провести в
треугольнике?
Каким свойством обладает точка пересечения медиан?
Какие треугольники называются равновеликими?
Сформулируйте свойство медианы треугольника применительно к его площади;
Каким свойством обладает точка пересечения медиан?
Какие треугольники называются равновеликими?
Сформулируйте свойство медианы треугольника применительно к его площади;
