Презентация, доклад на тему Гл. 1. Урок 7. Теорема Фалеса.

< А = < D
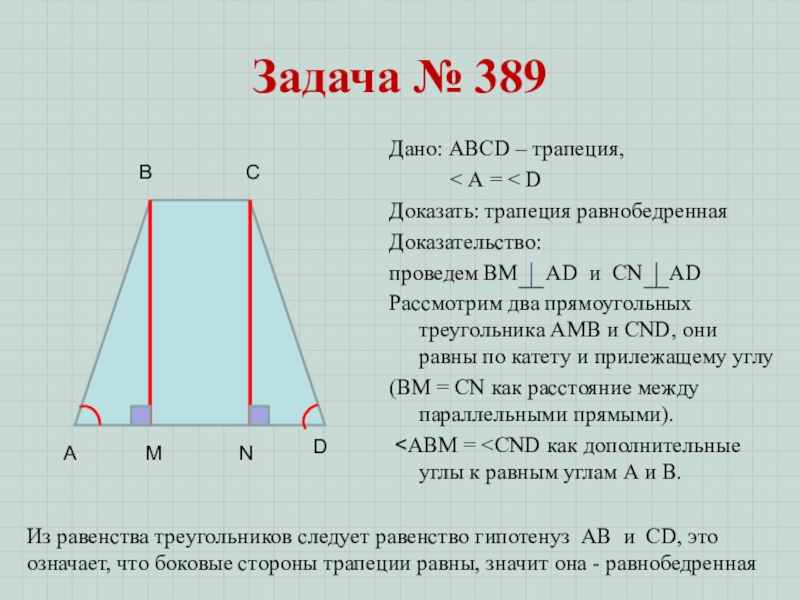
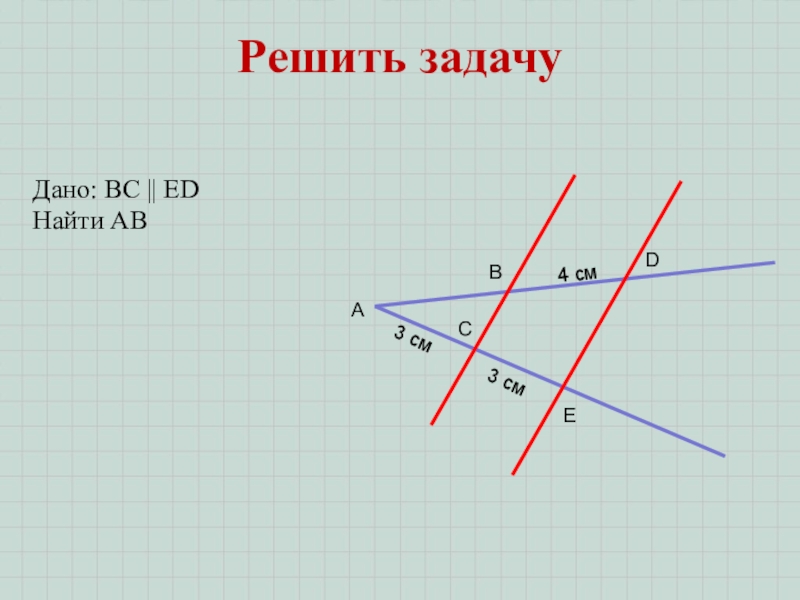
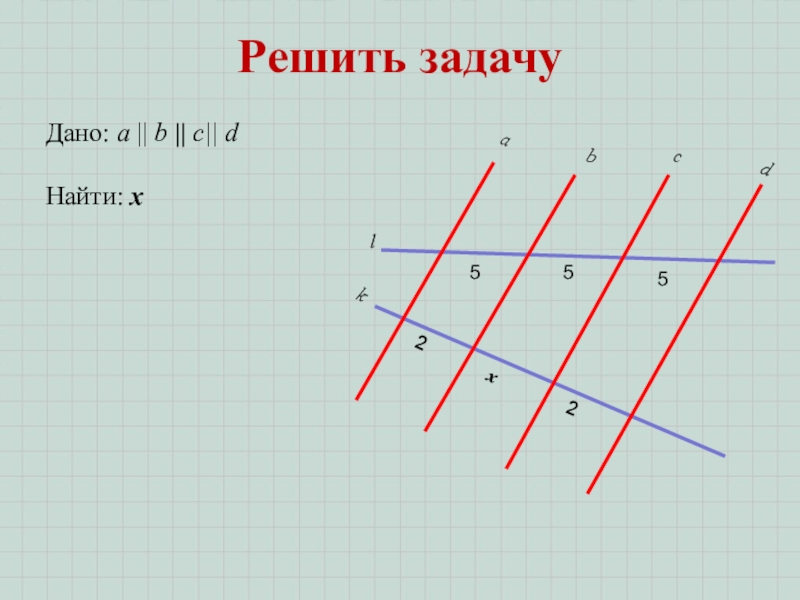
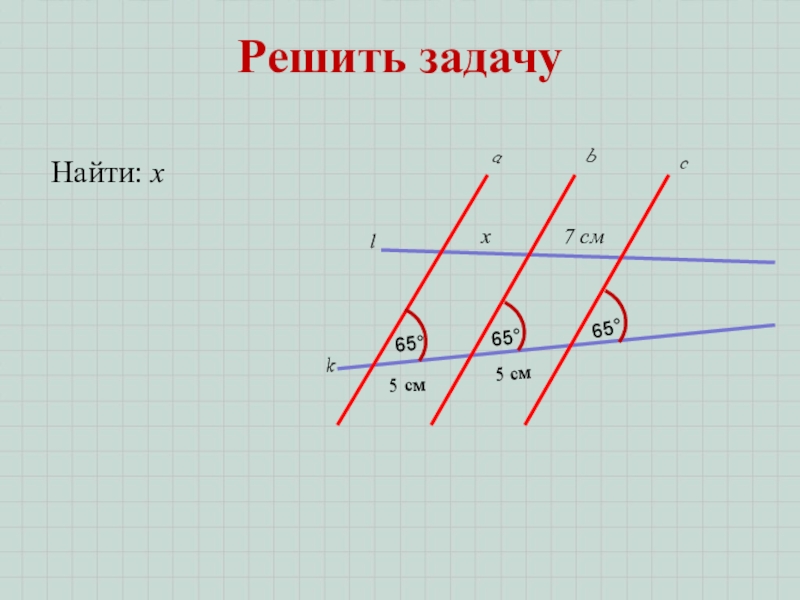
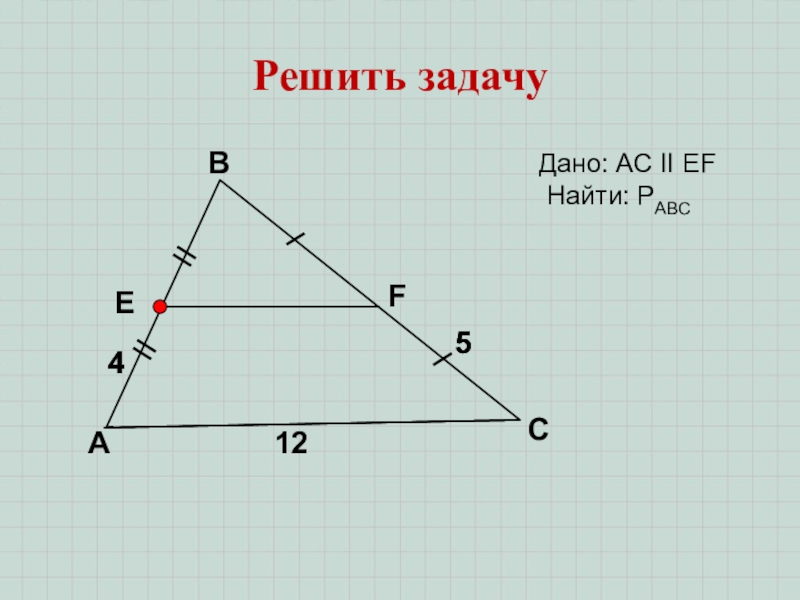
Доказать: трапеция равнобедренная
Доказательство:
проведем ВМ AD и CN AD
Рассмотрим два прямоугольных треугольника АМВ и CND, они равны по катету и прилежащему углу
(BM = CN как расстояние между параллельными прямыми).
<АВМ =

А

В

С

D

M

N

Из равенства треугольников следует равенство гипотенуз АB и CD, это означает, что боковые стороны трапеции равны, значит она - равнобедренная

существуют?
Перечислите свойства равнобедренной трапеции;

класс и тему «Деление отрезка пополам»

половины АВ;
2.Таким же радиусом проводим окружность с центром в т. В;
3. Пересечение окружностей даст точки С и D;
4.Проводим прямую СD, она пересечет прямую АВ в точке О;
Это и есть середина отрезка АВ

В

С

D

О

равные части?

одного из 7 мудрецов Древности, и которая подскажет нам способ, как делить отрезок на любое количество равных частей

одним из первых античных философов и основателем так называемой ионийской школы. Родился он в городе Милете, расположенном в Малой Азии, что на территории современной Турции, откуда и получил свое прозвище. Кроме философии, достиг особых познаний в астрономии и геометрии, благодаря изучению наследия египтян и ученых Месопотамии. Именно ему приписывается разделение календарного года на 365 дней. К сожалению, все мысли и изречения Фалеса Милетского дошли до нас только через труды позднейших философов.
 

стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN = NC.

Эта задача поможет нам доказать теорему Фалеса

и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

по учебнику № 384, 385);
Выполнить практическую работу: разделить отрезок на 11 равных частей при помощи циркуля и линейки без делений