- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Геометрия. Центральные и вписанные углы
Содержание
- 1. Геометрия. Центральные и вписанные углы
- 2. Следствие 1Вписанные углы, опирающиеся на одну и
- 3. Если все стороны многоугольника касаются окружности, то
- 4. Описанная окружностьЕсли все вершины многоугольника лежат на
- 5. Презентация к уроку математики в 8 классеПо
- 6. Актуализация знанийСформулируйте теорему о биссектрисе угла.Сформулируйте обратную
- 7. Что общего в них можно заметить с
- 8. каждая из сторон треугольника пересекает окружность
- 9. Определение: окружность называется вписанной в треугольник,
- 10. В любой треугольник можно вписать окружность.Дано:
- 11. Задача: в прямоугольный треугольник вписана окружность,
- 12. Задача: в прямоугольный треугольник вписана окружность,
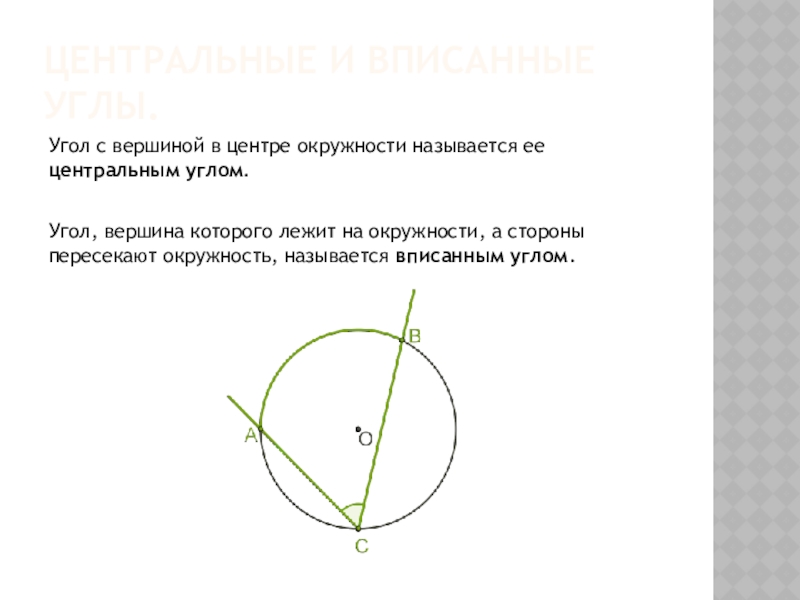
Слайд 1центральные и вписанные углы.
Угол с вершиной в центре окружности называется ее
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Слайд 2
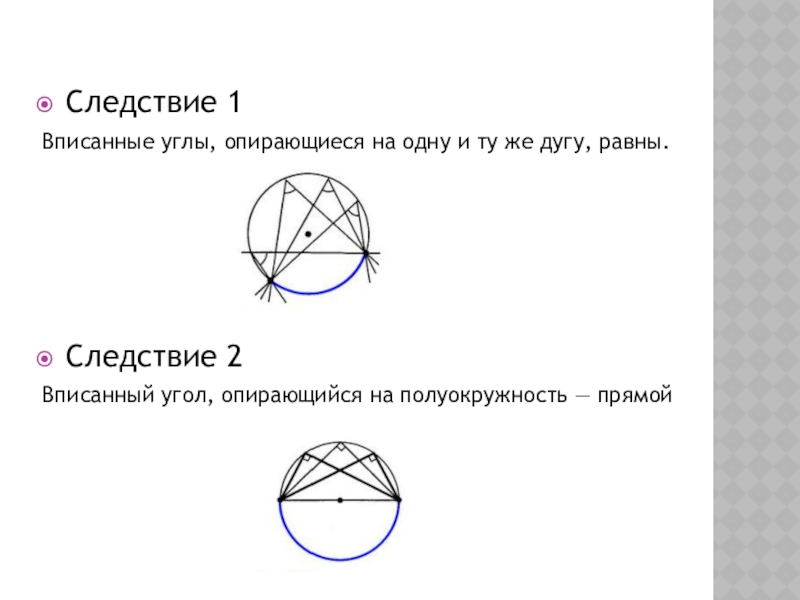
Следствие 1
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Следствие
Вписанный угол, опирающийся на полуокружность — прямой
Слайд 3Если все стороны многоугольника касаются окружности, то окружность называется вписанной в
Теорема
В любой треугольник можно вписать окружность.
Замечания
1) Отметим, что в треугольник можно вписать только одну окружность.
2) В отличие от треугольника не во всякий четырехугольник можно вписать окружность.
В любом описанном четырехугольнике суммы противоположных сторон равны.
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность
Вписанная окружность
Слайд 4Описанная окружность
Если все вершины многоугольника лежат на окружности, то окружность называется
Теорема
Около любого треугольника можно описать окружность.
Замечания
1) Отметим, что около треугольника можно описать только одну окружность.
2) В отличие от треугольника около четырехугольника не всегда можно описать окружность.
В любом вписанном четырехугольнике сумма противоположных углов равна 180°.
Слайд 5Презентация к уроку математики в 8 классе
По теме:
«Вписанная окружность»
Учебник «Геометрия,
Слайд 6Актуализация знаний
Сформулируйте теорему о биссектрисе угла.
Сформулируйте обратную теорему.
Сформулируйте свойство биссектрис треугольника.
Что
Сформулируйте теорему о срединном перпендикуляре к отрезку.
Сформулируйте свойство высот треугольника.
Слайд 7Что общего в них можно заметить с точки зрения геометрических фигур?
на
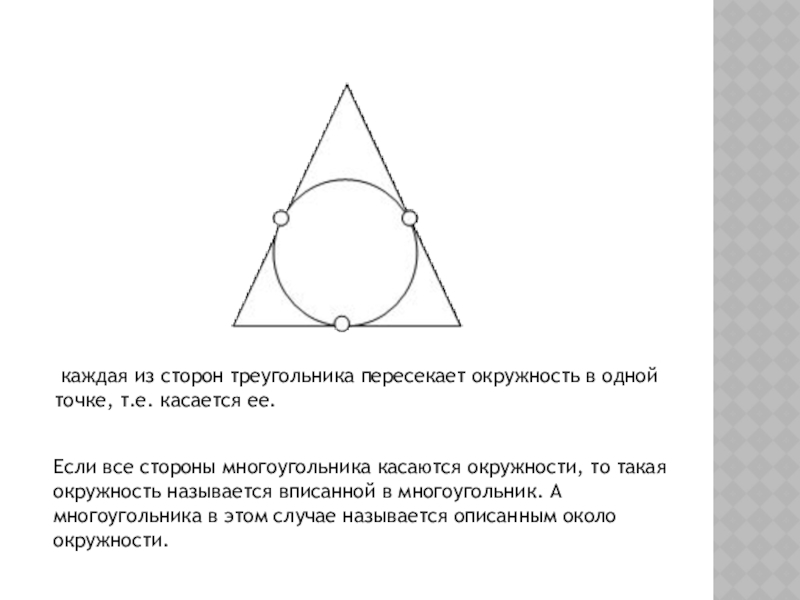
Слайд 8 каждая из сторон треугольника пересекает окружность в одной точке, т.е.
Если все стороны многоугольника касаются окружности, то такая окружность называется вписанной в многоугольник. А многоугольника в этом случае называется описанным около окружности.
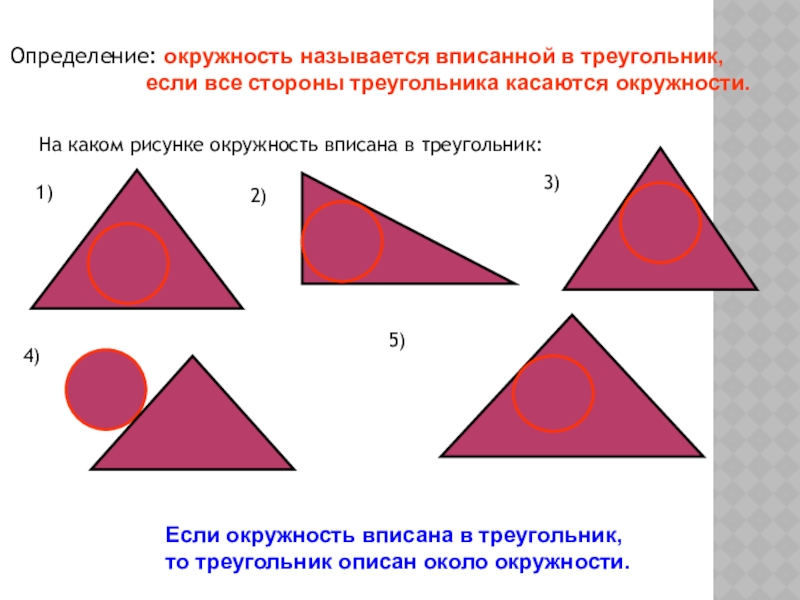
Слайд 9Определение: окружность называется вписанной в треугольник,
Если окружность вписана в треугольник,
то треугольник описан около окружности.
Слайд 10В любой треугольник можно вписать окружность.
Дано: АВС, окружность с центром
Доказать: окружность с центром в точке О вписана в треугольник DАВС
Доказательство
Рассмотрим АВС. Проведем биссектрисы треугольника, пересекающиеся в точке О. Проведем перпендикуляры ОК, ОL и ОM к сторонам АВС. Отметим равные отрезки ОК, ОL и ОM. Они равны, потому что ОК, ОL и ОM – радиусы одной и той же окружности.
Заметим АMO= АKO, по гипотенузе и острому углу: AO – общая, МАО=КАО, т.к. АО-биссектриса, АМО=АКО=90°.
Это значит, что OK=OM, аналогично можно доказать, что ОК=OL. Итак, окружность проходит через точки K, L, M, а стороны треугольника касаются окружности в точках K, L, M.
Значит, окружность с центром О радиуса ОК является вписанной в DАВС.
Слайд 11Задача: в прямоугольный треугольник вписана окружность,
Найдите радиус вписанной окружности.
Решение:
АВ = АМ + ВМ = 6 + 4 = 10(см)
По теореме Пифагора: АС2 + ВС2 = АВ2
,
АС= 6+ r, ВС = 4 + r
(6 + r)2 + (4 + r)2 = 102
Решив квадратное уравнение, получим r = 2 см
Ответ: 2 см
Слайд 12Задача: в прямоугольный треугольник вписана окружность, гипотенуза точкой касания делится
Найдите радиус вписанной окружности.