- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Геометрия 11 класс. Тема: Компланарные векторы
Содержание
- 1. Геометрия 11 класс. Тема: Компланарные векторы
- 2. Векторы называются компланарными, если
- 3. Три вектора, среди которых имеются два коллинеарных, также компланарны.Вывод:Компланарность трёх векторов
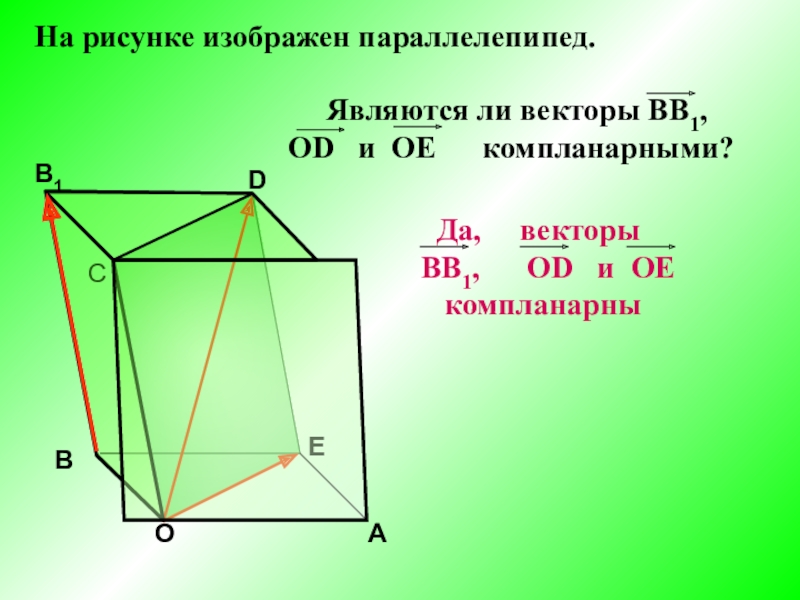
- 4. На рисунке изображен параллелепипед. АОЕDCВB1
- 5. АОЕDCВB1На рисунке изображен параллелепипед. ВЫВОД:Три
- 6. BCA1B1C1D1AD
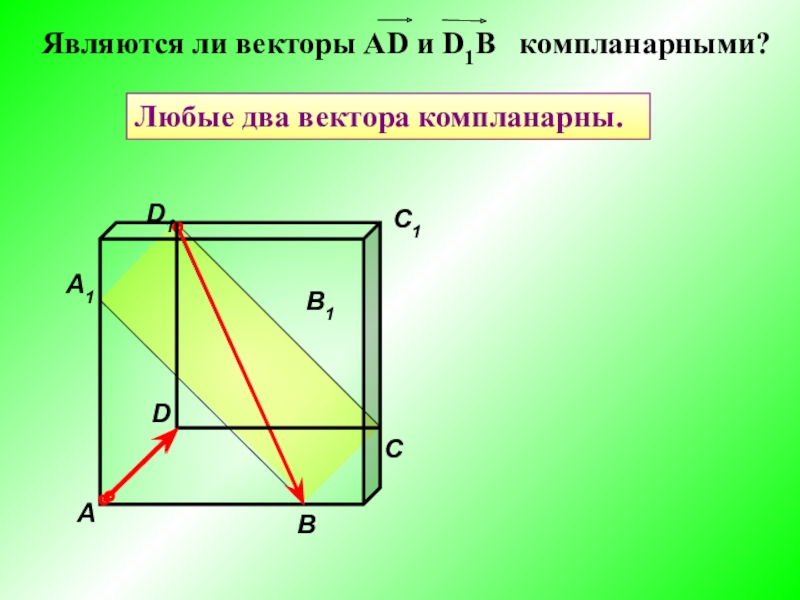
- 7. ABCA1B1C1D1DЛюбые два вектора компланарны.
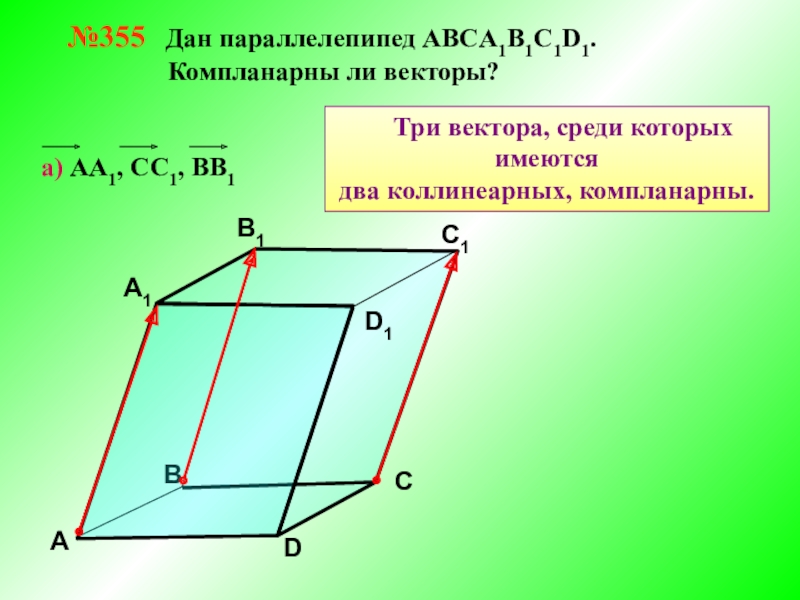
- 8. №355 Дан параллелепипед АВСA1B1C1D1.
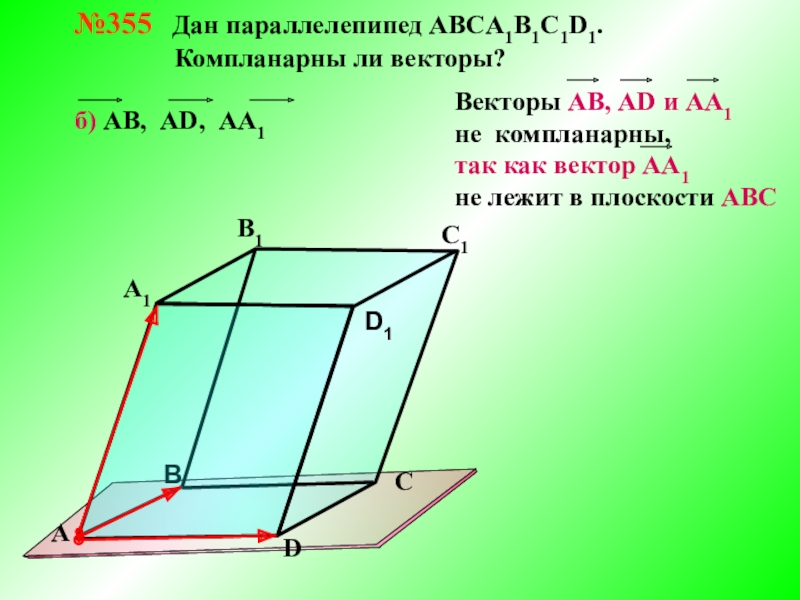
- 9. №355 Дан параллелепипед АВСA1B1C1D1.
- 10. Сделаем выводы:Три вектора, среди которых имеются два
- 11. Докажем, что векторы компланарны.В1
- 12. Слайд 12
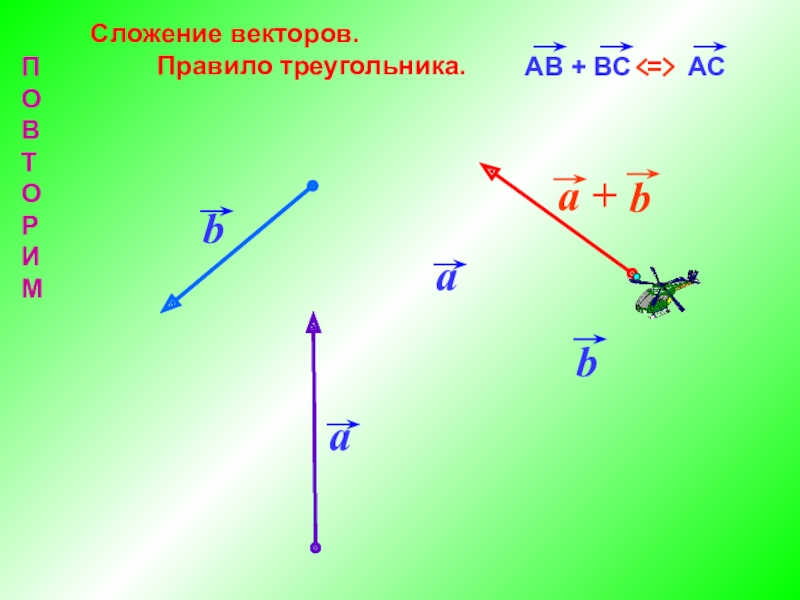
- 13. Сложение векторов. Правило треугольника.bПОВТОРИМ
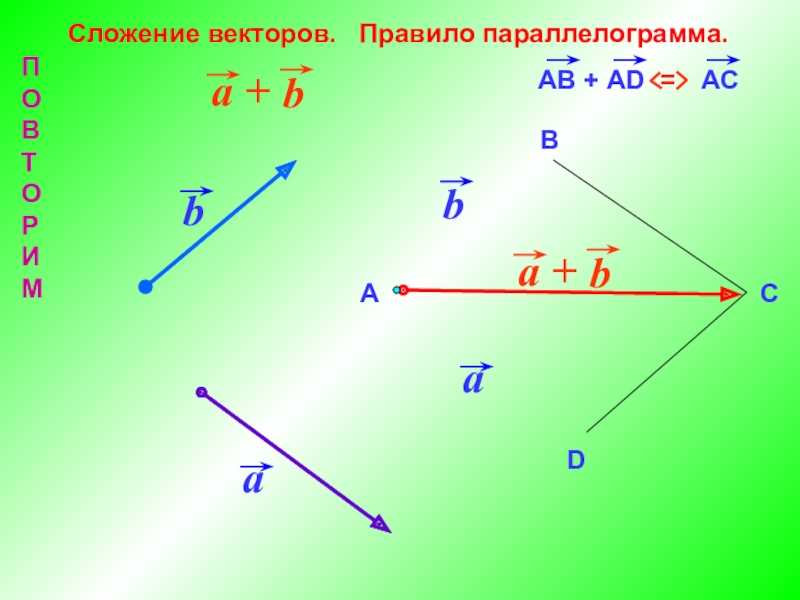
- 14. Сложение векторов. Правило параллелограмма.АВDCПОВТОРИМ
- 15. Сложение векторов. Правило многоугольника.ПОВТОРИМ
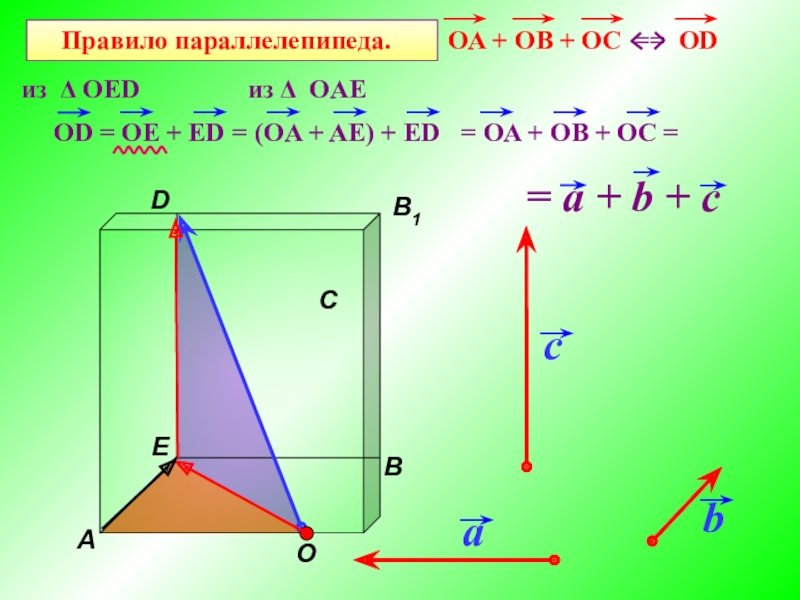
- 16. Правило параллелепипеда. bиз Δ OEDиз Δ OAE
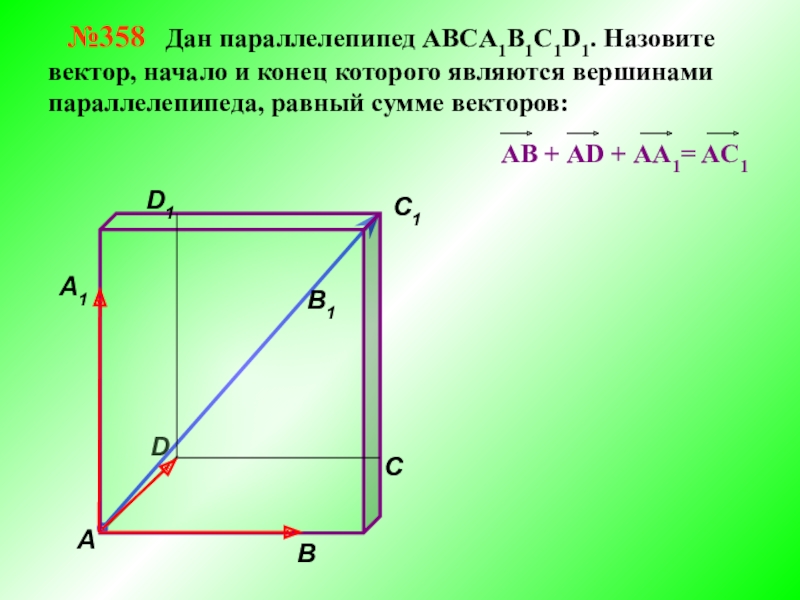
- 17. ВAС B1C1D1 №358 Дан параллелепипед
- 18. ВAСC1D1 №358 Дан параллелепипед АВСA1B1C1D1.
- 19. ВAСC1D1 №358 Дан параллелепипед АВСA1B1C1D1.
- 20. ВAСC1D1 №358 Дан параллелепипед АВСA1B1C1D1.
- 21. ВAСC1D1 №358 Дан параллелепипед АВСA1B1C1D1.
- 22. ВAСC1D1 №359 Дан параллелепипед АВСA1B1C1D1.
- 23. ВAСC1D1 №359 Дан параллелепипед АВСA1B1C1D1.
Слайд 2 Векторы называются компланарными, если при откладывании их от
Другими словами, векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Любые два вектора компланарны.
Определение компланарных векторов
Слайд 3
Три вектора, среди которых имеются два коллинеарных, также
Вывод:
Компланарность трёх векторов
Слайд 5
А
О
Е
D
C
В
B1
На рисунке изображен параллелепипед.
ВЫВОД:
Три произвольных вектора могут
Слайд 8
№355 Дан параллелепипед АВСA1B1C1D1.
В
А
В1
С1
D1
D
С
А1
Три вектора, среди которых имеются
два коллинеарных, компланарны.
Слайд 10Сделаем выводы:
Три вектора, среди которых имеются два коллинеарных, также компланарны.
Любые два
В решении вопроса о компланарности трёх векторов применим признак компланарности
Слайд 17
В
A
С
B1
C1
D1
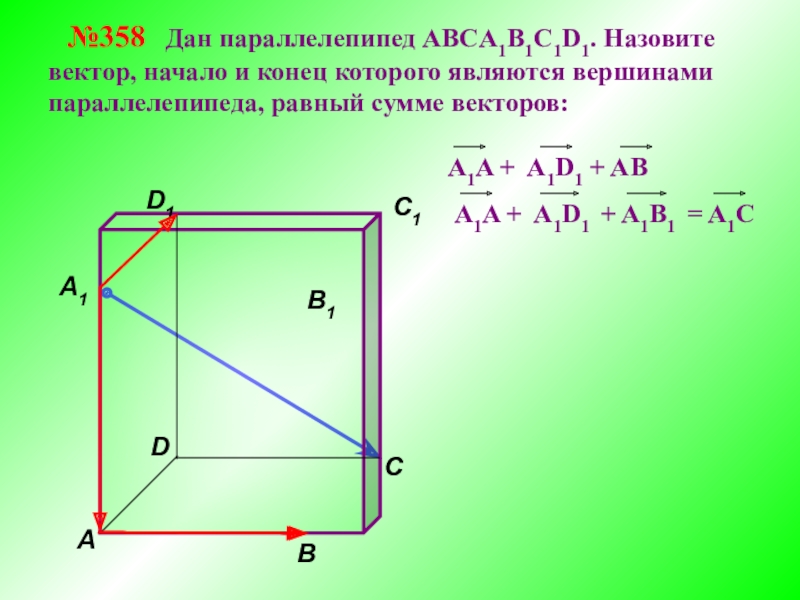
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало
АВ + АD + АА1
A1
Слайд 18В
A
С
C1
D1
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и
DА + DC + DD1
A1
B1
Слайд 19
В
A
С
C1
D1
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и
A1
B1
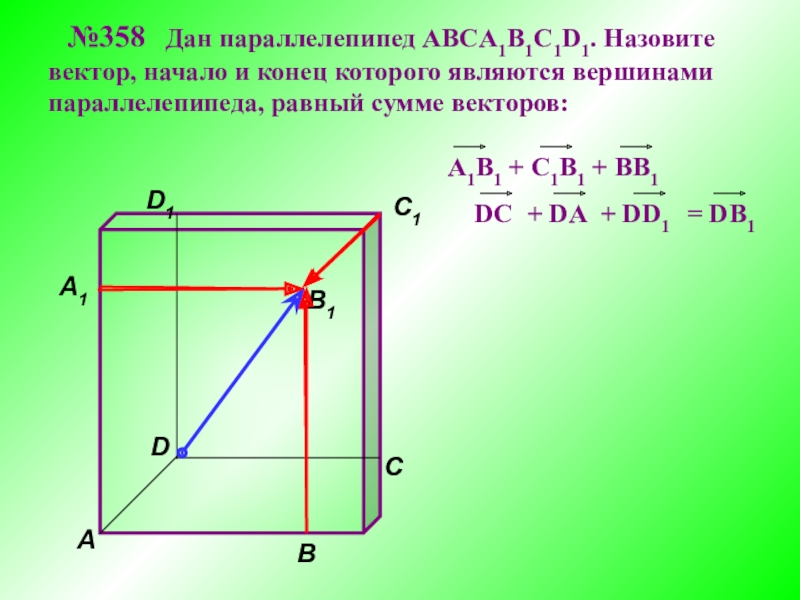
A1B1 + C1B1 + BB1
Слайд 20
В
A
С
C1
D1
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и
A1
B1
Слайд 21
В
A
С
C1
D1
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и
A1
B1
Слайд 22
В
A
С
C1
D1
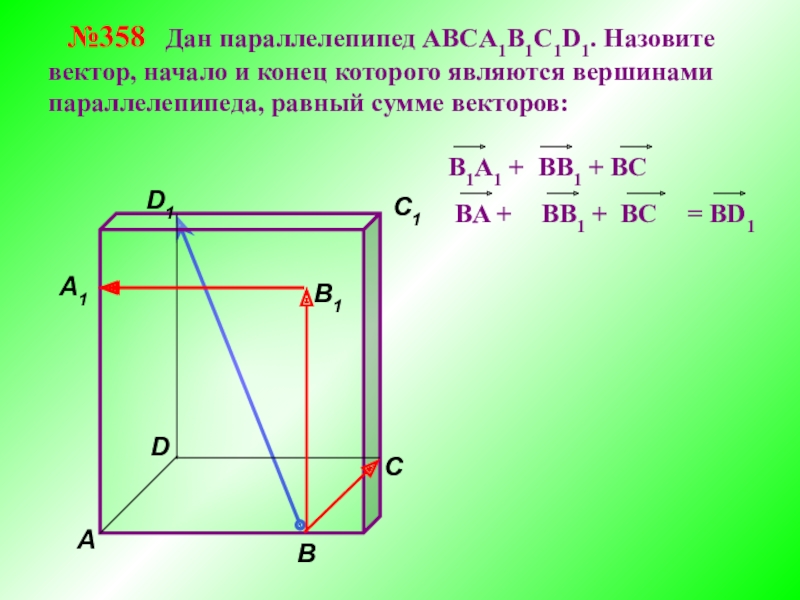
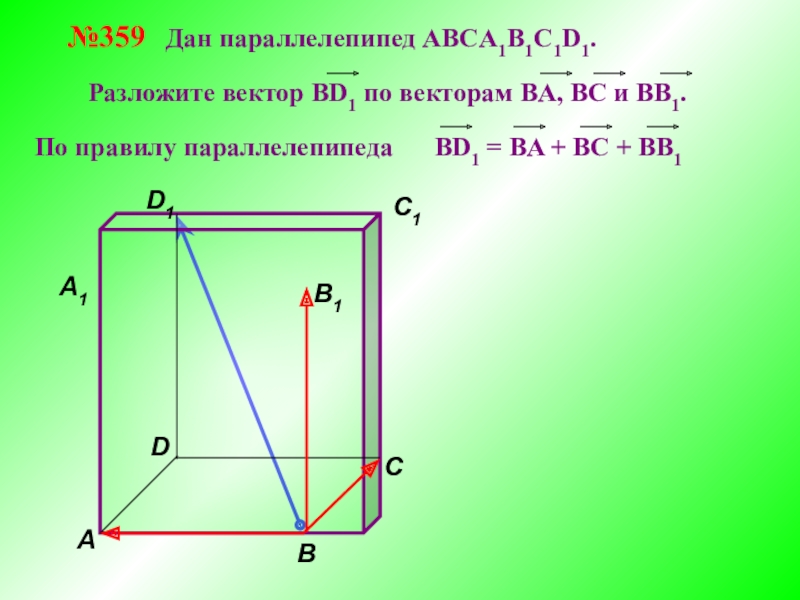
№359 Дан параллелепипед АВСA1B1C1D1.
A1
B1
Слайд 23
В
A
С
C1
D1
№359 Дан параллелепипед АВСA1B1C1D1.
A1
B1
из Δ А1В1B
=
=
=