учащаяся 9 «Б» класса
МБОУ СОШ № 5, г. Лысково.
Руководитель: Девочкина Татьяна Николаевна,
учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Геометрические паркеты
Содержание
- 1. Геометрические паркеты
- 2. Цель: Создание математического
- 3. Задачи: 1. Изучить информацию о возникновении и
- 4. Гипотеза: Можно создать бесчисленное множество различных паркетов.
- 5. Историческая справка В толковом
- 6. Математический паркет
- 7. Правильные паркетыПаркет называется правильным, если он состоит
- 8. Полуправильные паркеты Паркеты, состоящие из
- 9. Полуправильные (Архимедовы) паркеты
- 10. Усеченный шестиугольный паркетРомбошестиугольный паркет
- 11. . Некоторые определения паркета не ограничиваются
- 12. Мориц Корнелий Эшер (1898-1971) Из всех
- 13. Мориц Корнелий Эшер (1898-1971)«Мечтатели, сибиллы и пророки,
- 14. Паркеты Эшера «Если мы
- 15. Предел круга- одна из работ М.ЭшераЗдесь представлен
- 16. Предел круга Морица ЭшераМориц Эшер: "Иногда, когда
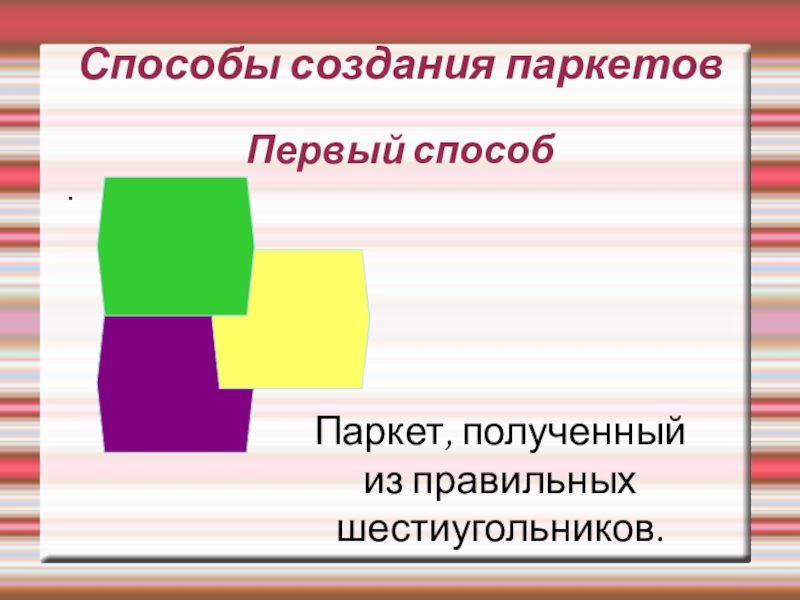
- 17. Способы создания паркетов Первый способ.Паркет, полученный из правильных шестиугольников.
- 18. Второй способПаркет, полученный в результатеобъединения пяти правильных треугольников
- 19. Третий способПаркет, полученный объединением паркета из греческих крестов и паркета из квадратов.
- 20. Четвертый способПаркет, полученный с помощью параллельного переноса звездчатых многоугольников.
- 21. Вывод:Цель работы достигнута.Выдвинутая мною гипотеза о бесконечном
- 22. Список литературы1. Васильев Н.Б. и др. Математические
- 23. Спасибо за внимание
Цель: Создание математического паркета.
Слайд 3Задачи:
1. Изучить информацию о возникновении и развитии паркетного искусства.
2. Что означает
математический паркет.
3. Какие существуют способы создания паркета.
3. Какие существуют способы создания паркета.
Слайд 5Историческая справка
В толковом словаре С.И.Ожегова , паркет
– это планки из твердых пород дерева для покрытия полов, а также само покрытие.
В России паркетные полы были нововведением Петра I, который привёз целый цех краснодеревщиков из Германии. В 19 веке знаменитые образцы художественного паркета выкладываются в Государственном Русском музее и Зимнем дворце. Технология со временем изменяется, и детали орнамента вырезаются не вручную, а на станках , в настоящее время с применением лазера и компьютера.
В России паркетные полы были нововведением Петра I, который привёз целый цех краснодеревщиков из Германии. В 19 веке знаменитые образцы художественного паркета выкладываются в Государственном Русском музее и Зимнем дворце. Технология со временем изменяется, и детали орнамента вырезаются не вручную, а на станках , в настоящее время с применением лазера и компьютера.
Слайд 6 Математический паркет
Определение:
В математике паркетом называют
замощение плоскости одинаковыми
фигурами, которые не перекрывают друг друга
и не оставляют на плоскости пустого
пространства
Слайд 7Правильные паркеты
Паркет называется правильным, если он состоит из правильных многоугольников и
вокруг каждой вершины многоугольники расположены одним и тем же способом. Существует три правильных замощения плоскости: треугольный, квадратный и шестиугольный паркеты
Слайд 8Полуправильные паркеты
Паркеты, состоящие из правильных многоугольников двух или
более типов, такие, что для любых двух вершин паркета существует преобразование симметрии переводящее одну из них в другую, называются полуправильными паркетами или архимедовыми паркетами
Слайд 9Полуправильные (Архимедовы) паркеты
Усеченный квадратный паркет
Курносый квадратный паркет
Тришестиугольный паркет
Изокурносый треугольный
Курносый квадратный паркет
Тришестиугольный паркет
Изокурносый треугольный
Слайд 10 Усеченный шестиугольный паркет
Ромбошестиугольный паркет
Ромбоусеченный тришестиугольный
Курносый тришестиугольный
Курносый тришестиугольный
Слайд 11.
Некоторые определения паркета не ограничиваются многоугольниками; в этом случае
паркетом называется покрытие плоскости без пропусков и перекрытий заданными фигурами.
Слайд 12Мориц Корнелий Эшер (1898-1971)
Из всех работ Эшера лучше всего
известны его орнаменты (или мозаики), то есть периодическое заполнение плоскости одинаковыми фигурами без их пересечений и щелей между ними. Разбивая плоскость на хитроумные комбинации контуров птиц, рыб, пресмыкающихся, млекопитающих и человеческих фигур, Эшер умело включает свои орнаменты в необычайные, подчас озадачивающие неожиданными решениями композиции.
Слайд 13Мориц Корнелий Эшер (1898-1971)
«Мечтатели, сибиллы и пророки,
Дорогами, запретными для мысли,
Проникли — вне сознания - далеко
Туда, где светят царственные числа»
В.Брюсов
Паркеты Эшера, с причудливым переплетением фигур людей, животных или монстров — это это не фантасмагория Сальвадора Дали или Рене Маргитта, а тонкие философские и математические наблюдения.
Туда, где светят царственные числа»
В.Брюсов
Паркеты Эшера, с причудливым переплетением фигур людей, животных или монстров — это это не фантасмагория Сальвадора Дали или Рене Маргитта, а тонкие философские и математические наблюдения.
Слайд 14Паркеты Эшера
«Если мы создаём мир, то пусть он
будет не абстрактным и туманным. Пусть он будет представлен конкретными узнаваемыми вещами».
Морис Эшер
Птицы
Рыбы Ящерицы
Морис Эшер
Птицы
Рыбы Ящерицы
Слайд 15Предел круга- одна из работ М.Эшера
Здесь представлен один из двух видов
неевклидового пространства,
описанных французским
математиком Пуанкаре.
Чтобы понять особенности
этого пространства, представьте,
что вы находитесь внутри самой
картины. По мере вашего перемещения
от центра круга к его границе,
ваш рост будет уменьшаться также,
как уменьшаются рыбы на данной картине.
Таким образом путь, который вам надо будет
пройти до границы круга будет казаться вам бесконечным.
Слайд 16Предел круга Морица Эшера
Мориц Эшер: "Иногда, когда я рисую,
мне кажется,
будто я медиум,
находящийся во власти существ,
порожденных моим же воображением.
Рыбы становятся птицами.
День ночью. Из хаоса рождается
Жизнь, она замирает в мертвых
городах, трансформируется
в шахматную партию и рассыпается
в пыль. Мозаика оживает и превращается в ящериц,
они движутся, живут
и вновь уходят в орнамент."
находящийся во власти существ,
порожденных моим же воображением.
Рыбы становятся птицами.
День ночью. Из хаоса рождается
Жизнь, она замирает в мертвых
городах, трансформируется
в шахматную партию и рассыпается
в пыль. Мозаика оживает и превращается в ящериц,
они движутся, живут
и вновь уходят в орнамент."
Слайд 19Третий способ
Паркет,
полученный
объединением
паркета из
греческих крестов
и паркета
из
квадратов.
Слайд 20Четвертый способ
Паркет, полученный
с помощью
параллельного
переноса
звездчатых
многоугольников.
Слайд 21Вывод:
Цель работы достигнута.
Выдвинутая мною гипотеза о
бесконечном множестве
правильных паркетов оказалась
неверна: в ходе работы я
выяснила, что правильных
паркетов только 11.
Слайд 22Список литературы
1. Васильев Н.Б. и др. Математические соревнования. Геометрия. - М.:
Наука, 1974, с. 15 /Библиотечка физико-математической школы, выпуск 4.
2. Доморяд А.П. Математические игры и развлечения. - М.; 1961.
3. Журнал //Квант. 1979. - № 2. - С.9; 1980. - № 2. - С.25; 1986 - № 8 - С 3* 1987. - № 6. - С.27; 1987. - № 11. - С.21; 1989. - № 11. - С.57.
4. Журнал //Математика в школе. 1967. – № 3. – С.75; 1986. № 1. – С.59;
5. Заславский А. Паркеты и разрезания //Квант. - 1999. - № 2. - С.32.
6. Кокстер Г.С.М. Введение в геометрию. - М.- Наука, 1966, с. 100.
7. Смирнова И.М. В мире многогранников. - М.: Просвещение, 1995.
8. Смирнова И.М., Смирнов В.А. Паркеты и их иллюстрации в графическом редакторе "Paint" //Математика в школе. - 2000. - № 8. - С.54.
2. Доморяд А.П. Математические игры и развлечения. - М.; 1961.
3. Журнал //Квант. 1979. - № 2. - С.9; 1980. - № 2. - С.25; 1986 - № 8 - С 3* 1987. - № 6. - С.27; 1987. - № 11. - С.21; 1989. - № 11. - С.57.
4. Журнал //Математика в школе. 1967. – № 3. – С.75; 1986. № 1. – С.59;
5. Заславский А. Паркеты и разрезания //Квант. - 1999. - № 2. - С.32.
6. Кокстер Г.С.М. Введение в геометрию. - М.- Наука, 1966, с. 100.
7. Смирнова И.М. В мире многогранников. - М.: Просвещение, 1995.
8. Смирнова И.М., Смирнов В.А. Паркеты и их иллюстрации в графическом редакторе "Paint" //Математика в школе. - 2000. - № 8. - С.54.