- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Геометрические методы решения задач на построение
Содержание
- 1. Геометрические методы решения задач на построение
- 2. Задача на построение состоит в том, что
- 3. Построения более сложных задач сводят к некоторым типичным комбинациям простейших построений, которые называются основными построениями.
- 4. Основные построенияОтложить на данном луче от его
- 5. Схема решения задач на построениеАнализПостроение ДоказательствоИсследование
- 6. 1. Метод пересечения множеств Сущность метода пересечения
- 7. ТЕОРЕМА. Три отрезка могут быть сторонами треугольника
- 8. Задача. Построить окружность, касательную к двум данным
- 9. ПостроениеИз произвольной точки А прямой a опускаем
- 10. ДоказательствоОкружность касается прямых, а и b, так
- 11. 2. Метод параллельного переносаСущность метода параллельного переноса
- 12. Задача. Построить трапецию по основанию , диагоналям
- 13. ПостроениеСтроим треугольник АСК по сторонам АС,СК и
- 14. Построить четырехугольник, зная его стороны и угол
- 15. Построение Строим треугольник АОD по двум сторонам
- 16. 3. Метод симметрии Две точки на плоскости
- 17. Задача. На данной прямой АВ найти точку
- 18. ПостроениеПостроим точку С, симметричную М относительно АВПостроим
- 19. :Метод вращения вокруг точки Пусть в плоскости
- 20. Построить квадрат так, чтобы три его вершины
- 21. ПостроениеПостроим образ С прямой с при вращении
Слайд 2Задача на построение состоит в том, что требуется построить наперед указанными
Слайд 3Построения более сложных задач сводят к некоторым типичным комбинациям простейших построений,
Слайд 4Основные построения
Отложить на данном луче от его начала отрезок, равный данному
Отложить от данного луча в данную полуплоскость угол, равный данному углу.
Построить треугольник по трем сторонам.
Построить треугольник по двум сторонам и углу между ними.
Построить треугольник по стороне и двум прилежащим углам.
Построить биссектрису данного неразвернутого угла.
Построить серединный перпендикуляр данного отрезка
Построить середину данного отрезка.
Построить прямую, проходящую через данную точку и перпендикулярную данной прямой.
Построить прямую, проходящую через данную точку и параллельную данной прямой.
Построить прямоугольный треугольник по гипотенузе и острому углу.
Построить прямоугольный треугольник по гипотенузе и катету.
Построить касательную к окружности, проходящую через данную на ней точку
Слайд 61. Метод пересечения множеств
Сущность метода пересечения состоит в следующем. Задачу сводят
Методы решения задач на построение
Слайд 7
ТЕОРЕМА.
Три отрезка могут быть сторонами треугольника тогда и только тогда,
Слайд 8Задача. Построить окружность, касательную к двум данным параллельным прямым a и
Анализ.
Если расстояние между прямыми a и b обозначим d, то радиус окружности равен d/2. Задача сводится к нахождению центра окружности, удовлетворяющего двум условиям:
1) центр равноудален от прямых a и b;
2) центр отстоит от точки Р на расстояние d/2.
● Р
d
a
b
Слайд 9Построение
Из произвольной точки А прямой a опускаем перпендикуляр АВ на прямую
Строим серединный перпендикуляр к отрезку АВ
Строим множество точек, отстоящих от Р на расстояние d/2, то есть окружность L (P; d/2) с центром в точке Р и радиуса d/2
Строим пересечение L (P; d/2) и с
Строим окружность L1 (O; OP), где О принадлежит пересечению L (P; d/2) и с
a
b
●А
●
B
● P
c
●
●
О
Слайд 10Доказательство
Окружность касается прямых, а и b, так как по построению центрокружности
Исследование
Возможны три случая расположения точки Р относительно прямых, а и b.
1. Если точка Р лежит между прямыми, а и b, то существуют две окружности, то есть множество L (P; d/2) состоит из двух точек.
2. Если Р принадлежит одной из прямых, а и b, то задача имеет единственное решение.
3. Если точка Р лежит вне полосы, ограниченной прямыми, а и b, то задача не имеет решения.
а
b
• P
a
b
a
b
• P
•
P
Слайд 112. Метод параллельного переноса
Сущность метода параллельного переноса заключается в том, что
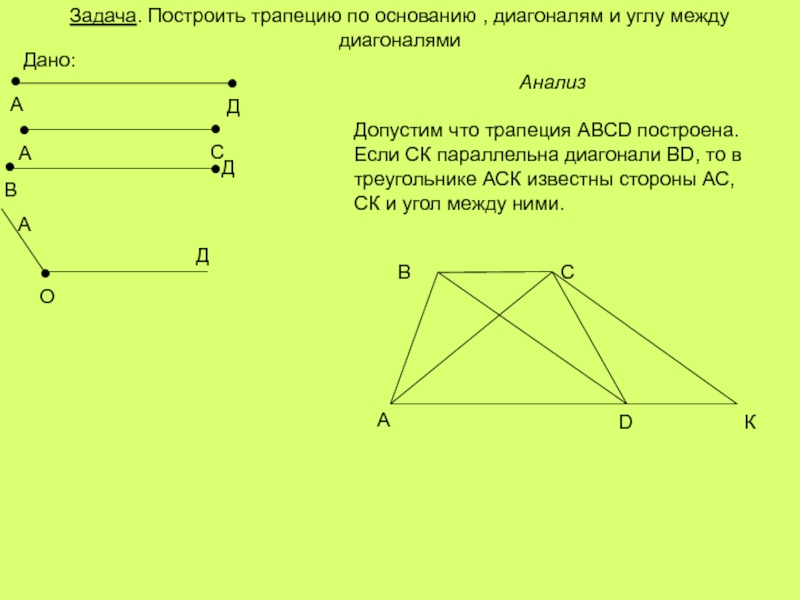
Слайд 12Задача. Построить трапецию по основанию , диагоналям и углу между диагоналями
Дано:
●А
●Д
●А
●С
●В
●Д
●
О
Д
А
Анализ
Допустим
А
В
С
К
D
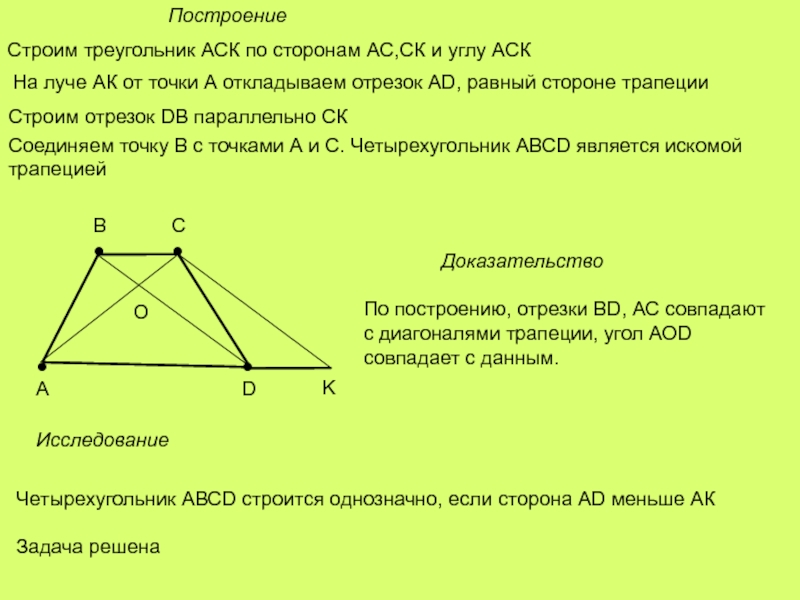
Слайд 13Построение
Строим треугольник АСК по сторонам АС,СК и углу АСК
На луче АК
Строим отрезок DВ параллельно СК
Соединяем точку В с точками А и С. Четырехугольник АВСD является искомой трапецией
Доказательство
По построению, отрезки ВD, АС совпадают с диагоналями трапеции, угол АОD совпадает с данным.
Исследование
Четырехугольник АВСD строится однозначно, если сторона АD меньше АК
Задача решена
●
A
B●
С
●
●D
K
О
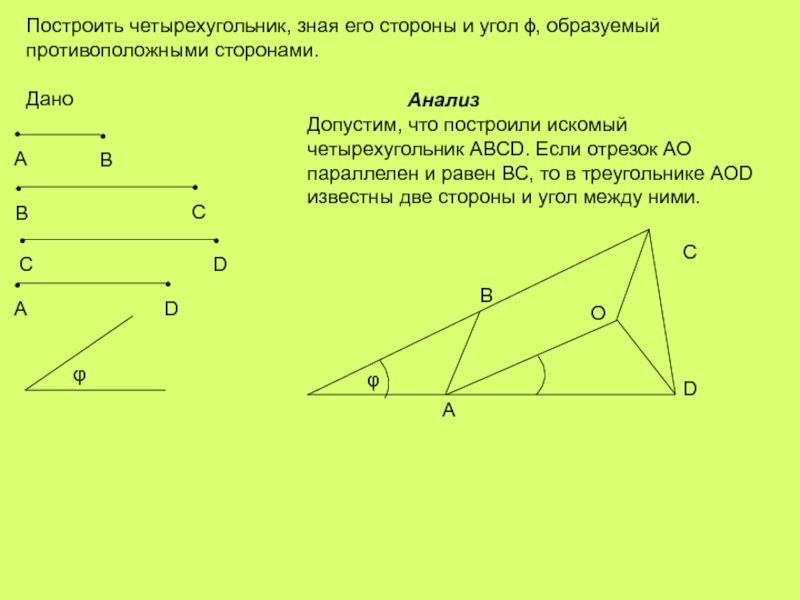
Слайд 14Построить четырехугольник, зная его стороны и угол ϕ, образуемый противоположными сторонами.
Дано
•
A
•B
•
B
•
C
•D
•
C
•A
•
D
Допустим, что построили искомый четырехугольник АВСD. Если отрезок АО параллелен и равен ВС, то в треугольнике АОD известны две стороны и угол между ними.
A
B
C
D
O
φ
φ
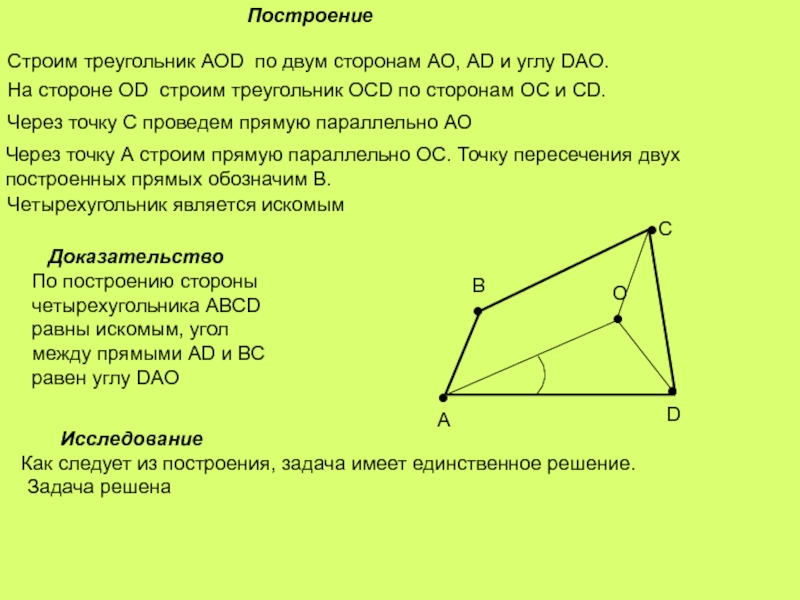
Слайд 15Построение
Строим треугольник АОD по двум сторонам АО, АD и углу
На стороне ОD строим треугольник ОСD по сторонам ОС и СD.
Через точку С проведем прямую параллельно АО
Через точку А строим прямую параллельно ОС. Точку пересечения двух построенных прямых обозначим В.
Четырехугольник является искомым
●
A
B●
●D
O●
●С
Доказательство
По построению стороны четырехугольника АВСD равны искомым, угол между прямыми АD и ВС равен углу DAO
Исследование
Как следует из построения, задача имеет единственное решение.
Задача решена
Слайд 16
3. Метод симметрии
Две точки на плоскости называются симметричными относительно прямой
Метод симметрии заключается в следующем. Предполагают задачу решенной и одной из данных точек отражают в какой-нибудь известной оси. Тогда полученную симметричную точку подчиняют тем же условиям, которым должна быть удовлетворять замененная точка. Причем за ось симметрии выбирается по возможности данная прямая или прямая, которая может быть легко построена. Полученную задачу решают методами и способами ранее известными.
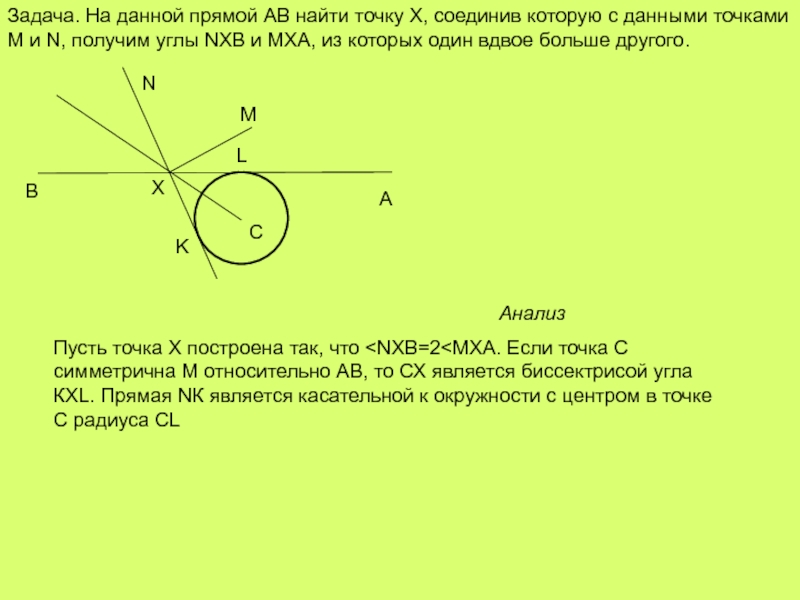
Слайд 17Задача. На данной прямой АВ найти точку Х, соединив которую с
А
B
N
M
X
L
C
Анализ
Пусть точка Х построена так, что K
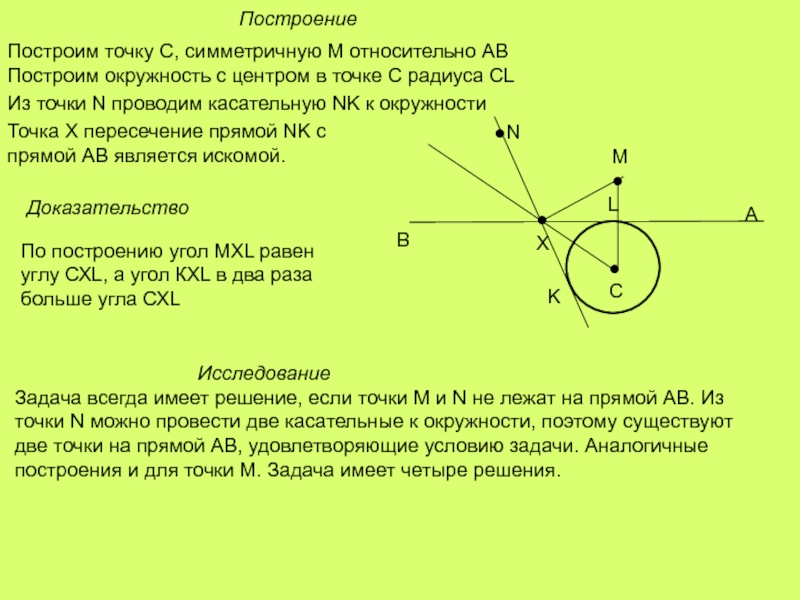
Слайд 18Построение
Построим точку С, симметричную М относительно АВ
Построим окружность с центром в
Из точки N проводим касательную NK к окружности
Точка Х пересечение прямой NK с прямой АВ является искомой.
B
●N
M●
●X
L
●C
K
A
Доказательство
По построению угол МХL равен углу СХL, а угол КХL в два раза больше угла СХL
Исследование
Задача всегда имеет решение, если точки М и N не лежат на прямой АВ. Из точки N можно провести две касательные к окружности, поэтому существуют две точки на прямой АВ, удовлетворяющие условию задачи. Аналогичные построения и для точки М. Задача имеет четыре решения.
Слайд 19:
Метод вращения вокруг точки
Пусть в плоскости даны точки ориентированный угол α.
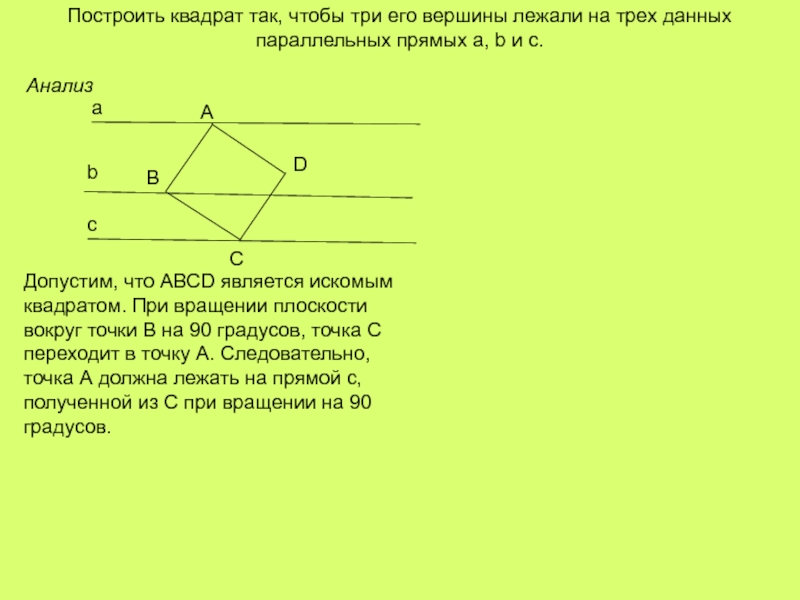
Слайд 20Построить квадрат так, чтобы три его вершины лежали на трех данных
Анализ
Допустим, что АВСD является искомым квадратом. При вращении плоскости вокруг точки В на 90 градусов, точка С переходит в точку А. Следовательно, точка А должна лежать на прямой с, полученной из С при вращении на 90 градусов.
А
В
С
D
a
b
c
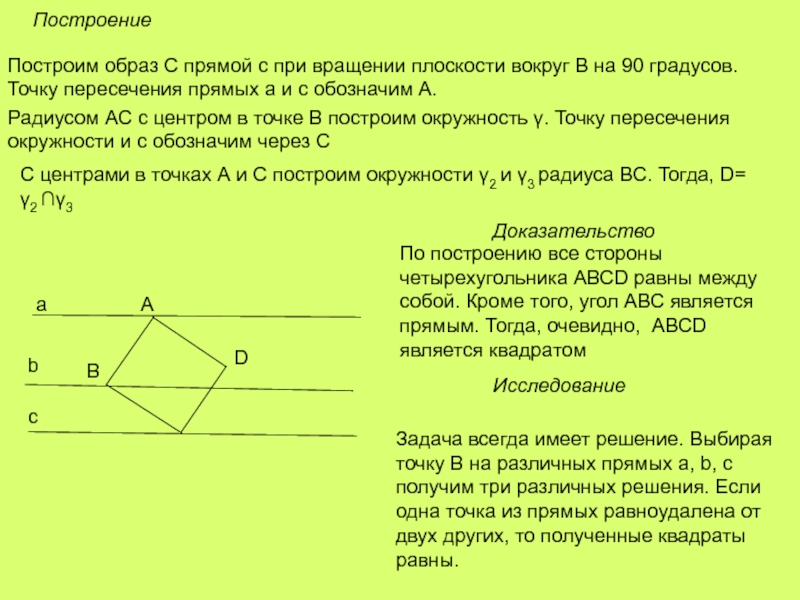
Слайд 21Построение
Построим образ С прямой с при вращении плоскости вокруг В на
Радиусом АС с центром в точке В построим окружность γ. Точку пересечения окружности и с обозначим через С
С центрами в точках А и С построим окружности γ2 и γ3 радиуса ВС. Тогда, D= γ2 ∩γ3
Доказательство
По построению все стороны четырехугольника АВСD равны между собой. Кроме того, угол АВС является прямым. Тогда, очевидно, АВСD является квадратом
Исследование
Задача всегда имеет решение. Выбирая точку В на различных прямых а, b, c получим три различных решения. Если одна точка из прямых равноудалена от двух других, то полученные квадраты равны.
А
В
D
b
c
a